Выше были рассмотрены некоторые виды модуляции, определяющие тот или иной радиосигнал. В самом общем виде радиосигнал может быть представлен в виде квазигармонического сигнала:

. (6.20)

Как правило, спектр такого сигнала сосредоточен вокруг частоты , а его ширина . В этом смысле сигнал (6.20) считается узкополосным.

При преобразовании узкополосного сигнала радиотехническими цепями необходимо сохранить закон изменения того параметра сигнала, в котором заложена передаваемая информация. В частном случае это может быть изменение амплитуды(амплитудная модуляция) или частоты(частотная модуляция). Следует отметить, что эти изменения происходят гораздо медленнее изменения несущей частоты. Это особенность радиосигналов позволяет существенно упростить решения задач их преобразования различными узкополосными частотно-избирательными цепями, к которым относятся рассмотренные выше простейшие колебательные контура и активная цепь в виде резонансного усилителя.

Представим огибающую и текущую фазу сигнала (6.20) следующим образом

, (6.21)

. (6.22)

При анализе преобразования сигнала вида (6.20) частотно-избирательной цепью в качестве и обычно выступают сигналы, связанные преобразованием Гильберта

; . (6.23)

Сигнал называется сопряжённым по Гильберту с сигналом , а преобразование Гильберта физически означает фазовый сдвиг всех составляющих сигнала на угол в области положительных и на угол в области отрицательных частот. Очевидно, спектры сигналов и связаны соотношением

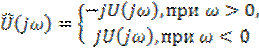(6.24)

Возвратимся к выражениям (6.21) и (6.22). Эти выражения можно представить как модуль и аргумент некоторого комплексного сигнала

, (6.25)

который называется аналитическим сигналом, соответствующим физическому сигналу . Очевидно, физический сигнал представляет собой вещественную часть аналитического сигнала, т.е. .

Так как аналитический сигнал является комплексным, его можно представить в следующем виде

,

или с учётом (6.21) и (6.22) в виде выражения

, (6.26)

где

(6.27)

называется комплексной огибающей аналитического сигнала.

Найден спектр аналитического сигнала. Применив к (6.25) прямое преобразование Фурье, получим:

, (6.28)

или с учётом соотношения (6.24)

. (6.29)

С другой стороны, преобразование Фурье выражения (6.26) даст

. (6.30)

Сопоставление (6.29) и (6.30) показывает, что

или что то же самое

. (6.31)

Таким образом, с одной стороны, спектральная плотность комплексной огибающей равна удвоенной спектральной плотности физического сигнала, а с другой стороны – сосредоточена в низкочастотной области положительных частот (рис. 6.3). Это позволяет заменить задачу анализа преобразования узкополосного сигнала частотно-избиратель-ной цепью задачей анализа преобразования комплексной огибающей аналитического сигнала некоторой эквивалентной цепью, частотные характеристики которой также располагаются в низкочастотной области. Такая цепь получила название низкочастотного

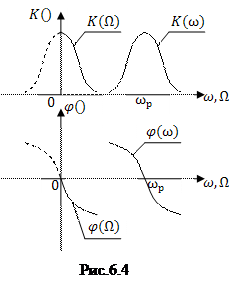
Рис. 6.3 эквивалента частотно-избирательной цепи.

Найдём характеристики низкочастотного эквивалента резонансного усилителя малых сигналов, рассмотренного в 5.5.3. Представим комплексный коэффициент передачи (5.73) с учётом (5.49) в виде

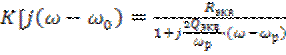. (6.32)

Введем обозначения

и .

Тогда (6.32) можно представить следующим образом

. (6.33)

Но (6.33) представляет собой комплексный коэффициент передачи интегрирующей цепи. Таким образом, низкочастотным эквивалентом резонансного усилителя, т.е. цепи второго порядка, является интегрирующая цепь, т.е. цепь первого порядка. Это существенно упрощает определения комплексной огибающей на выходе низкочастотного эквивалента.

На рис. 6.4. изображены графики АЧХ и ФЧХ частотно-избирательной цепи и её низкочастотного эквивалента (сплошные кривые в низкочастотной области). Очевидно, что импульсная характеристика низкочастотного эквивалента

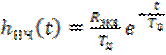. (6.34)

Перейдём к рассмотрению задачи преобразования узкополосного сигнала частотно-избирательной цепью. Пусть на вход цепи с резонансной частотой поступает сигнал

.

В общем случае частота несущего колебания не совпадает с резонансной частотой цепи, т.е. имеет место расстройка

.

Тогда входной сигнал можно записать следующим образом

. (6.35)

где

. (6.36)

Поскольку частотно-избирательная цепь является избирательной цепью, на её выходе также будет иметь место квазигармонический сигнал вида

. (6.37)

Аналитические сигналы, соответствующие входному и выходному сигналам

,

, (6.38)

где и - комплексные огибающие.

Ввиду того, что физический сигнал (6.37) представляет вещественную часть аналитического сигнала (6.38), т.е.

, (6.39)

то для его нахождения необходимо определить комплексную амплитуду . Комплексная огибающая, как подчёркивалось выше, представляет собой реакцию низкочастотного эквивалента цепи на комплексную огибающую входного аналитического сигнала. Эту задачу можно решить либо спектральным методом, либо методом интеграла наложения.

В соответствии со спектральным методом

.

С другой стороны, с учётом (6.30) и (6.32), имеем

. (6.40)

Применяя к (6.40) обратное преобразование Фурье, можно найти и, в соответствии с (6.39), - физический выходной сигнал .

Что касается метода интеграла наложения, то комплексная огибающая выходного аналитического сигнала определяется следующим образом

, (6.41)

где – импульсная характеристика низкочастотного эквивалента цепи.