2.2. Примесная проводимость полупроводников
Проводимость полупроводников определяется двумя типами носителей заряда, их концентрацией, которая зависит от примесей и температуры.
2.1. Собственная проводимость
Собственная проводимость полупроводников с точки зрения кристаллической структуры.
Полупроводник, в узлах кристаллической решетки которого расположены только собственные атомы, называется собственным.
|
|
||
|
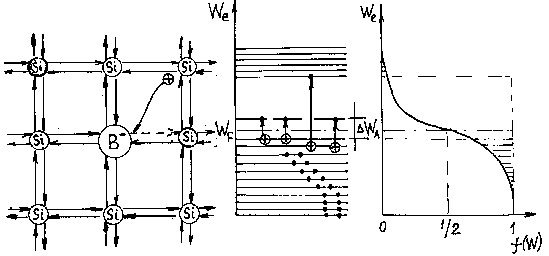
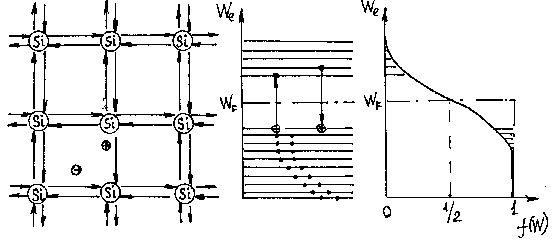
Рисунок 2.1а – Генерация пар зарядов с точки зрения кристаллической структуры |
Рисунок 2.1б – С точки зрения зонной теории |
Рисунок 2.1в – Зависимость f(W) от W при Т>0 |
Рисунок 2.1 - Схема образования электрона и дырки (термогенерация).
а) T = 0 К – случай рассмотрен выше. Если приложить электрическое поле, то тока не появится, т. к. нет свободных носителей заряда.
б) T > 0 К– при тепловых колебаниях атомов в решетке кристалла могут быть разорваны некоторые ковалентные связи , в результате чего в междоузельном пространстве появляются свободные электроны (рисунок 2.1а), а покинутое электроном место имеет избыточный положительный заряд, называемый дыркой. Дырка может быть занята электроном из соседней связи, при этом пустое место–дырка переместится в эту соседнюю связь и т. д. Следовательно, перемещение дырки по кристаллу можно рассматривать, как движение положительного заряда. Свободный электрон и дырка будут перемещаться по кристаллу хаотически в отсутствии электрического поля и направленно при наличии поля, создавая электронную и дырочную составляющие электрического тока. Процесс возникновения электронно–дырочных пар называется генерацией. На образование одной пары расходуется энергия, необходимая для разрыва ковалентной связи (Ge–0,72 B, Si–1,1 эВ, GaAs–1,41 эВ ).
Концентрация собственных электронов определяется температурой:
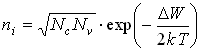
![]() ,
,
где ![]() – эффективная плотность состояний в зоне проводимости,
– эффективная плотность состояний в зоне проводимости,
![]() – эффективная плотность состояний в валентной зоне.
– эффективная плотность состояний в валентной зоне.
После подстановки численных значений физических констант ![]() ,
, ![]() ,
, ![]() и введения относительных выражений для эффективных масс
и введения относительных выражений для эффективных масс ![]() и
и ![]() и температуры
и температуры ![]() , получится следующая формула для вычисления
, получится следующая формула для вычисления ![]() :
:
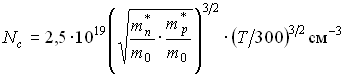
![]() – рассчитывается аналогично, и в инженерных расчетах
– рассчитывается аналогично, и в инженерных расчетах ![]() . Если
. Если ![]() (
(![]() – масса покоя электрона) и
– масса покоя электрона) и ![]() К, то
К, то ![]() .
.
Аналогично рассчитывается концентрация собственных дырок при ![]() К и
К и ![]() эВ
эВ ![]() ,
, ![]() . А в кремнии при этой же температуре
. А в кремнии при этой же температуре ![]() . Т. к.
. Т. к. ![]() , то
, то
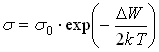 .
.
При встрече электрона с дыркой происходит рекомбинация.
Скорость рекомбинации, т. е. количество исчезающих в единицу времени электронно–дырочных пар равна:
![]() ,
,
где ![]() – коэффициент рекомбинации.
– коэффициент рекомбинации.
Процессы термогенерации и рекомбинации электронов и дырок идут одновременно.
При установившемся равновесии ![]() .
.
Это условие определяет равновесную концентрацию носителей заряда ![]() в собственном полупроводнике при заданной температуре.
в собственном полупроводнике при заданной температуре.
Разрыв ковалентной связи и образование пары электрон–дырка описывается, как переход электрона из валентной зоны в зону проводимости, на что тратится энергия равная ширине запрещенной зоны (рисунок 2.1б). Свободный электрон может двигаться в зоне проводимости (энергетический интервал между уровнями в которой очень мал ![]() эВ), свободная дырка может двигаться только в валентной зоне, ее энергия на энергетической диаграмме возрастает вниз. Функция распределения Ферми меняет вид (рисунок 2.1в): заштрихованные “хвосты” одинаковы по величине и в зоне проводимости, и в валентной зоне показывают, что вероятность образования электрона и дырки одинаковы. Рекомбинация электрона и дырки соответствует переходу электрона из зоны проводимости на свободный уровень валентной зоны.
эВ), свободная дырка может двигаться только в валентной зоне, ее энергия на энергетической диаграмме возрастает вниз. Функция распределения Ферми меняет вид (рисунок 2.1в): заштрихованные “хвосты” одинаковы по величине и в зоне проводимости, и в валентной зоне показывают, что вероятность образования электрона и дырки одинаковы. Рекомбинация электрона и дырки соответствует переходу электрона из зоны проводимости на свободный уровень валентной зоны.
2.2. Примесная проводимость полупроводников
2.2.1. Донорная проводимость
Донорная проводимость возникает в полупроводниках, которые легированы примесью с валентностью, большей валентности собственных атомов. Например, в ![]() (валентность
(валентность ![]() ) вводятся атомы
) вводятся атомы ![]() или
или ![]() (валентность
(валентность ![]() ).
).
а)Донорная проводимость с точки зрения кристаллической решетки
|
|
||
|
Рисунок 2.2а – Образование свободных носителей заряда с точки зрения кристаллической решетки |
Рисунок 2.2б - С точки зрения зонной теории |
Рисунок 2.2в - Зависимость |
Рисунок 2.2 - Схема появления свободных электронов за счет доноров.
Пятый электрон атома ![]() не участвует в создании ковалентных связей и оказывается наиболее слабо связанным. Он легко отрывается за счет энергии теплового движения, становится свободным и способен создавать электронный ток при наличии электрического поля. Этот процесс аналогичен ионизации атома в газе. При таком образовании свободного электрона не наблюдается разрыв ковалентных связей и образование дырки. Атом примеси становится положительным ионом, но он по–прежнему прочно “сидит” в узле решетки (рисунок 2.2а). Такие примеси называют донорными, а полупроводник донорным, электронным или п–типа. Как правило, при комнатной температуре все доноры ионизированы и
не участвует в создании ковалентных связей и оказывается наиболее слабо связанным. Он легко отрывается за счет энергии теплового движения, становится свободным и способен создавать электронный ток при наличии электрического поля. Этот процесс аналогичен ионизации атома в газе. При таком образовании свободного электрона не наблюдается разрыв ковалентных связей и образование дырки. Атом примеси становится положительным ионом, но он по–прежнему прочно “сидит” в узле решетки (рисунок 2.2а). Такие примеси называют донорными, а полупроводник донорным, электронным или п–типа. Как правило, при комнатной температуре все доноры ионизированы и ![]() (
(![]() – концентрация доноров, обычно
– концентрация доноров, обычно ![]() для
для ![]() ). Кроме того, происходит и процесс генерации пар электрон–дырка, но в таком полупроводнике электронов значительно больше, чем дырок:
). Кроме того, происходит и процесс генерации пар электрон–дырка, но в таком полупроводнике электронов значительно больше, чем дырок: ![]() , а
, а ![]() . Электроны в таком полупроводнике называются основными носителями заряда, дырки неосновными. При этом не нарушается электрическая нейтральность полупроводника.
. Электроны в таком полупроводнике называются основными носителями заряда, дырки неосновными. При этом не нарушается электрическая нейтральность полупроводника.
б) С точки зрения зонной теории положение пятого электрона атома примеси на энергетической диаграмме изображают помещенным на примесном (донорном) уровне, расположенным в верхней половине запрещенной зоны, вблизи зоны проводимости.я ![]() соответствует энергии необходимой для отрыва электрона от атома (например для
соответствует энергии необходимой для отрыва электрона от атома (например для ![]() в
в ![]()
![]() эВ). Этому процессу соответствует переход электрона с донорного уровня в зону проводимости. Концентрация свободных электронов за счет донорной примеси и ее зависимость от температуры оценивается следующим выражением:
эВ). Этому процессу соответствует переход электрона с донорного уровня в зону проводимости. Концентрация свободных электронов за счет донорной примеси и ее зависимость от температуры оценивается следующим выражением:
![]() .
.
Вероятность появления электрона в зоне проводимости в донорном полупроводнике значительно больше вероятности образования дырки в валентной зоне, что отражается графиком распределения Ферми. Уровень Ферми в донорных полупроводниках лежит в верхней половине запрещенной зоны (рисунок 2.2б, 2.2в). По-прежнему возможны процессы рекомбинации, но при каждой температуре устанавливается равновесие.
Концентрация электронов в зоне проводимости определяется выражением:
![]() .
.
Если обозначить концентрацию дырок в донорном полупроводнике, то справедливо соотношение ![]() . Отсюда можно определить концентрацию дырок в донорном полупроводнике
. Отсюда можно определить концентрацию дырок в донорном полупроводнике
2.2.2. Акцепторная проводимость
Акцепторная проводимость наблюдается в полупроводниках, легированных примесью, с валентностью меньше валентности основного атома. Например, ![]() ,
, ![]() ,
, ![]() в
в ![]() .
.
а)Акцепторная проводимость с точки зрения кристаллической решетки. Одна связь около атома ![]() оказывается незаполненной. При
оказывается незаполненной. При ![]() электрон соседних атомов может перейти, заполнив эту связь (рисунок 2.3а).
электрон соседних атомов может перейти, заполнив эту связь (рисунок 2.3а).
В результате атом ![]() становится отрицательным ионом, “сидящим” в узле решетки, а около атома кремния, от которого “ушел” электрон образовалась дырка. Свободные электроны при этом не образуются. Энергия образования дырки мала (например, для
становится отрицательным ионом, “сидящим” в узле решетки, а около атома кремния, от которого “ушел” электрон образовалась дырка. Свободные электроны при этом не образуются. Энергия образования дырки мала (например, для ![]() в
в ![]()
![]() эВ; для
эВ; для ![]() в
в ![]()
![]() эВ).
эВ).
Примесь, благодаря которой появляются дырки, называется акцепторной, а полупроводник акцепторным, дырочным или ![]() -типа.
-типа.
|
|
||
|
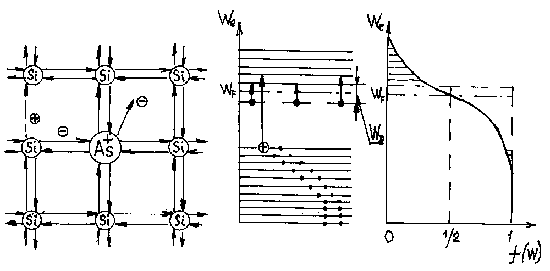
Рисунок 2.3.а – Образование свободных носителей заряда с точки зрения кристаллической решетки |
Рисунок 2.3б – С точки зрения зонной теории |
Рисунок 2.3в – Зависимость |
Рисунок 2.3 - Схема образования дырки за счет акцепторной примеси.
Одновременно проходит термогенерация электронно–дырочных пар, но дырок больше ![]() и они являются основными носителями, а электроны неосновными.
и они являются основными носителями, а электроны неосновными.
б) С точки зрения зонной теории положение свободного места, на котором может быть захвачен электрон изображается акцепторным уровнем, расположенным в нижней половине запрещенной зоны (рисунок 2.3б). Расстояние между уровнем акцептора и потолком валентной зоны соответствует энергии образования дырки, т. е. электрон переходит из валентной зоны на примесный уровень. Концентрация дырок, появившихся за счет акцепторных примесей оценивается выражением:
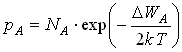 ,
,
где NА– концентрация акцепторов. В таких полупроводниках вероятность появления дырки в валентной зоне больше, чем вероятность появления электрона в зоне проводимости. Это отражено графиком функции Ферми и положением уровня Ферми (рисунок 2.3в).
Как правило, в реальных полупроводниках есть и донорные акцепторные примеси. Они компенсируют друг друга, и тип полупроводника определяется разностью концентраций примеси. Например, если ![]() , то полупроводник
, то полупроводник ![]() -типа и концентрация дырок определяется разностью
-типа и концентрация дырок определяется разностью ![]() . И наоборот.
. И наоборот.


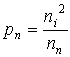 .
.