Одним из эффективных и широко применяемых в различных вариантах методов борьбы с помехами является метод накопления. Сущность метода состоит в том, что сигнал или его элементы многократно повторяются. На приеме отдельные образцы сигнала сличаются (обычно суммируются), и так как различные образцы по-разному искажаются помехой в силу независимости последних, то можно восстановить переданный сигнал с большей достоверностью.
В простейшей форме метод накопления часто применяется при телефонном разговоре в условиях плохой слышимости, когда переспрашивают и повторяют одно и то же слово по нескольку раз.
В случае телеграфной связи каждая кодовая комбинация, состоящая из элементов 0 и 1, передается несколько раз. Если вероятность сбоя символов 1 и 0 одинакова, то на приеме решение выносится «по большинству», т. е. воспроизводится символ 1 на данной позиции, когда их число на этой позиции больше числа символов 0, и, наоборот, воспроизводится 0, когда число «нулей» больше числа «единиц»:
переданная комбинация 01001
первая принятая 00001
вторая 11010
третья 01101
воспроизведенная комбинация 01001
Заметим, что можно было бы получить п образцов сигнала не путем их повторения во времени, а путем передачи по независимым каналам, разделенным по частоте, или каким-либо другим способом.
Существуют и другие разновидности метода накопления. К ним, в частности, относится метод синхронного накопления, нашедший применение в радиолокации. При этом методе на протяжении посылки сигнала берется не один отсчет, а несколько. На приеме эти отсчеты суммируются в накопителе.
Пусть отдельные отсчеты принятого сигнала:
![]() ,
,![]() ,…
,…![]() (4.1)
(4.1)
тогда сумма отсчетов
![]()
![]()
![]() (4.2)
(4.2)
Величина b = ns представляет собой полезный сигнал на выходе
приемника. Случайная величина ![]() представляет собой помеху. Отношение сигнала к помехе на выходе приемника
представляет собой помеху. Отношение сигнала к помехе на выходе приемника ![]() равно:
равно: ![]() (4.3)
(4.3)
Здесь мы полагали, что ![]() некоррелированы и имеют одинаковое распределение,
некоррелированы и имеют одинаковое распределение, ![]() отношение сигнала к помехе на входе приемника.
отношение сигнала к помехе на входе приемника.
Таким образом, при описанных условиях накопление отсчетов сигнала позволяет увеличить отношение сигнала к помехе на выходе приемника ровно в п раз. Суть дела сводится к тому, что мощность сигнала при суммировании растет пропорционально п2 (складываются напряжения), а мощность помехи — пропорционально п (суммируются мощности). Поэтому отношение сигнала к помехе увеличивается в п раз, если помехи независимы. При наличии корреляции между значениями помехи этот выигрыш будет меньше.
Метод накопления можно осуществить, беря не сумму отсчетов xk, а интеграл непрерывно изменяющейся функции x(t)=s+![]() (t) за время Т, равное длительности сигнала,
(t) за время Т, равное длительности сигнала,
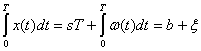
Здесь b — также постоянная, выражающая сигнал на выходе накопителя (интегратора), а |![]() — случайная величина, определяющая помеху на выходе интегратора.
— случайная величина, определяющая помеху на выходе интегратора.
Определим дисперсию случайной величины ![]()
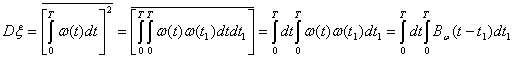 (4.4.)
(4.4.)
где ![]() — функция корреляции помехи
— функция корреляции помехи ![]() . Если спектр помехи равномерен в достаточно широкой полосе частот F, т. е. интервал корреляции помехи
. Если спектр помехи равномерен в достаточно широкой полосе частот F, т. е. интервал корреляции помехи ![]() , то конечные пределы интегрирования могут быть заменены на бесконечные:
, то конечные пределы интегрирования могут быть заменены на бесконечные:
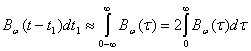 (4.5)
(4.5)
где ![]() . По определению (2.24) интервал корреляции
. По определению (2.24) интервал корреляции
![]() (4.6)
(4.6)
В рассматриваемом случае ![]() и
и ![]() . Следовательно,
. Следовательно, ![]()
Тогда отношение сигнала к помехе на выходе интегратора будет
![]() (4.7)
(4.7)
Итак, выигрыш, получаемый при интегрировании, тем больше, чем больше отношение ![]() . Описанный способ приема называется интегральным.
. Описанный способ приема называется интегральным.
Заметим, что ![]() есть число независимых отсчетов помехи на интервале Т. Это означает, что ф-лы (4.3) и (4.7) совпадают, т. е. замена суммирования независимых значений непрерывным интегрированием дополнительного выигрыша не дает. Однако практическая реализация метода интегрирования осуществляется проще, чем суммирование дискретных значений. Так, при приеме телеграфных сигналов в качестве интегратора широко используется цепочка RC, разряжаемая синхронно по окончании каждой элементарной посылки (рис. 4.2). В конце каждой посылки заряд на емкости приблизительно пропорционален интегралу входного сигнала. Додетекторное интегрирование можно осуществить с помощью резонатора большой добротности.
есть число независимых отсчетов помехи на интервале Т. Это означает, что ф-лы (4.3) и (4.7) совпадают, т. е. замена суммирования независимых значений непрерывным интегрированием дополнительного выигрыша не дает. Однако практическая реализация метода интегрирования осуществляется проще, чем суммирование дискретных значений. Так, при приеме телеграфных сигналов в качестве интегратора широко используется цепочка RC, разряжаемая синхронно по окончании каждой элементарной посылки (рис. 4.2). В конце каждой посылки заряд на емкости приблизительно пропорционален интегралу входного сигнала. Додетекторное интегрирование можно осуществить с помощью резонатора большой добротности.
В простейшем случае таким резонатором может быть колебательный контур.
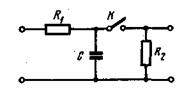
Рис. 4.2. Простейшая схема интегратора

