В качестве примера определим потенциальную помехоустойчивость систем с амплитудной и частной модуляцией.
Амплитудная модуляция. В этом случаи сигнал имеет вид
![]()
Тогда
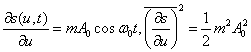
Согласно (9.19) энергетический спектр помехи на выходе приёмника ![]()
![]() (9.22)
(9.22)
Мощность сигнала на входе преемника равна:
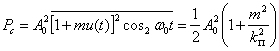
Здесь мы полагаем, что в спектре сообщения u(t) содержатся частоты более низкие, чем ω![]() , и отсутствует постоянная составляющая
, и отсутствует постоянная составляющая ![]() . Обобщенный выигрыш
. Обобщенный выигрыш ![]() при АМ согласно (9.17) равен:
при АМ согласно (9.17) равен:
![]() (9.23)
(9.23)
При синусоидальной модуляции (![]() ) и
) и ![]()
![]() . В общем случае при линейной модуляции сигнал можно записать виде
. В общем случае при линейной модуляции сигнал можно записать виде
![]() (9.24)
(9.24)
Для такого сигнала
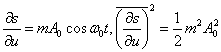 .
.
Спектр помехи на выходе оптимального приемника согласно (9.19)
![]() (9.25)
(9.25)
В частном случае, когда ![]() , получаем результат для амплитудной модуляции (9,22). При
, получаем результат для амплитудной модуляции (9,22). При ![]() будем иметь двухполосную (балансную) модуляцию (БМ)
будем иметь двухполосную (балансную) модуляцию (БМ)
![]()
В этом случае![]() и согласно (9.17)
и согласно (9.17)
![]() (9.26)
(9.26)
Таким образом, выигрыш в системе БМ не зависит ни от коэффициента модуляции, ни от пикфактора сообщения. При синусоидальной модуляции и m=1 выигрыш в системе БМ втрое больше, чем в системе AM. При одинаковой пиковой мощности сигнала ![]() в системе БМ в четыре раза больше, чем в системе AM.
в системе БМ в четыре раза больше, чем в системе AM.
В случае передачи одной боковой полосы (ОМ) энергетический спектр помехи на выходе приемника равен:
![]() (9.27)
(9.27)
Мощность сигнала
![]()
Тогда
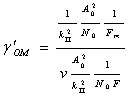
Системы ОМ и БМ по помехоустойчивости равноценны. Однако полоса частот сигнала в системе ОМ в два раза меньше, чем в системе БМ.
Частотная модуляция. Для этого вида модуляции сигнал
![]() где
где ![]()
Тогда
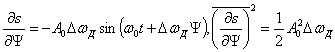
и согласно (9.21)
![]() (9.29)
(9.29)
После этого на основании (9.17) получаем выражение для выигрыша системы
![]() (9.30)
(9.30)
Из сравнения ф-л (9.23), (9.26), (9.28) и (9.30) следует, что наибольшей помехоустойчивостью обладает система с частотной модуляцией. В этой системе выигрыш γ увеличивается с увеличением индекса модуляции. Это означает, что увеличение помехоустойчивости достигается в системе ЧМ ценой расширения полосы частот, занимаемой сигналом, т. е. ценой введения в сигнал избыточности по частоте.

