1.1. Нелинейные элементы и их характеристики. Способы аппроксимации характеристик нелинейных элементов

1.2. Анализ преобразования гармонического сигнала НЭ при степенной аппроксимации ВАХ

1.3. Анализ преобразования гармонического сигнала НЭ при кусочно-линейной аппроксимации ВАХ

1.1. Нелинейные элементы и их характеристики. Способы аппроксимации характеристик нелинейных элементов

В общем случае нелинейная цепь описывается оператором преобразования W_нц:

u_вых(t) = W_нц[U_вх(t),t], (1.1)

для которого свойство линейности не выполняется. В состав такой цепи входят один или несколько нелинейных элементов (НЭ). Различают резистивные и реактивные НЭ. В качестве резистивных НЭ выступают транзисторы, полупроводниковые диоды, электронные лампы. Примером реактивного НЭ является варикап.

При анализе НЭ предполагается, что переходные процессы в НЭ заканчиваются практически с окончанием изменения входного сигнала, т.е. НЭ является безынерционным.

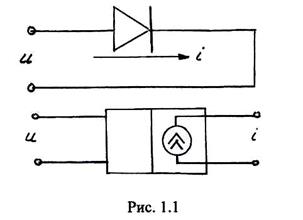В подавляющем большинстве задач радиотехники рассматриваются резистивные безынерционные НЭ. В таких элементах в качестве входного сигнала выступает напряжение, а в качестве выходного – ток, протекающий по элементу. На Рис.1.1 показаны: нелинейный двухполюсник – полупроводниковый диод и четырехполюсник, которым может быть представлен транзистор. Основной характеристикой НЭ является его вольт-амперная характеристика (ВАХ), т.е. зависимость тока, протекающего через НЭ, от приложенного к нему напряжения:

Другими характеристиками НЭ являются (Рис 1.2):

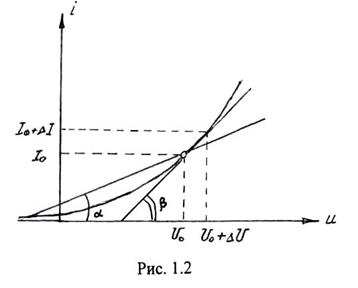– статическое сопротивление или сопротивление НЭ по постоянному току:

, (1.2)

– статическая крутизна:

, (1.3)

– дифференциальное сопротивление:

, (1.4)

– дифференциальная крутизна:

. (1.5)

Статическая крутизна пропорциональна тангенсу угла α, а динамическая тангенсу угла β – угла наклона касательной ВАХ в рабочей точке.

Замена истинной (реальной) ВАХ приближенно представляющей функцией называется аппроксимацией характеристики.

Степенная аппроксимация – представление ВАХ в виде ряда Тейлора в окрестности рабочей точки (I₀, U₀):

i=f(u)=a₀+a₁(u-U₀)+a₂(u-U₀)²+… (1.6)

Кусочно-линейная аппроксимация – представление ВАХ отрезками прямых с различными наклонами. На практике ограничиваются двумя отрезками:

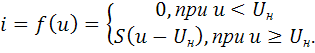(1.7)

Здесь – напряжение начала характеристики;

– крутизна наклона характеристики;

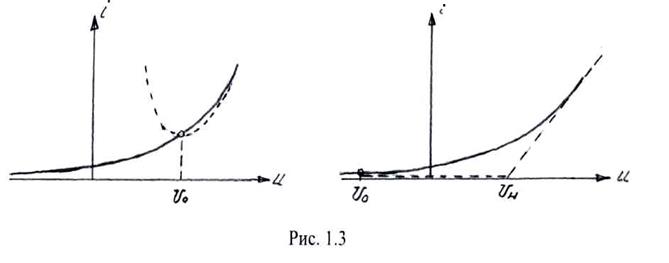
Аппроксимации (1.6) и (1.7) показаны на Рис. 1.3.

1.2. Анализ преобразования гармонического сигнала НЭ при степенной аппроксимации ВАХ

На Рис. 1.4 изображены ВАХ нелинейного элемента, график входного сигнала:

u(t)=U₀+U_mcosω₀t, (1.8)

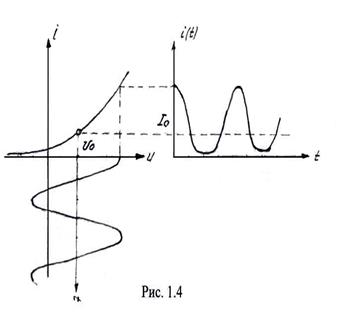и график выходного сигнала (тока, протекающего через НЭ). Форма тока существенно отличается от формы напряжения приложенного к нему. Воспользуемся степенной аппроксимацией ВАХ, ограничившись слагаемым третьей степени. Подставляя (1.8) в (1.6) и используя тригонометрические соотншения:

,

.

получим выражение для тока, протекающего через нелинейный элемент:

i(t)=I₀+I₁cosω₀t+I₂cos2ω₀t+ I₃cos3ω₀t+…, (1.9)

где ; ; ; (1.10)

Ток, протекающий через НЭ, содержит постоянную составляющую и совокупность гармоник, количество которых определяется наибольшей степенью аппроксимирующего полинома. При этом амплитуды четных гармоник определяются четными коэффициентами аппроксимирующего полинома, а нечетных гармоник – нечетными коэффициентами.

Анализ преобразования суммы двух гармонических сигналов при степенной аппроксимации ВАХ полиномом второй степени:

i=a₀+a₁(u-U₀)+a₂(u-U₀)². (1.11)

Входным сигналом в этом случае является колебание:

u(t)=U₀+U_m1cosω₁t+U_m2cosω₂t. (1.12)

Подстановка (1.12) в (1.11) и использование ранее приведенных тригонометрических соотношений и соотношения:

,

дает выражение для тока, протекающего через НЭ:

i(t)=I₀+I₁₁cosω₁t+I₁₂cosω₂t+I₂₁cos2ω₁t+I₂₂cos2ω₂t+

I_pcos(ω₁ – ω₂)t+ I_ccos(ω₁ + ω₂)t, (1.13)

где: ]; ; ; ; ; ;

. (1.14)

В этом случае ток, протекающий через НЭ содержит постоянную составляющую , гармоники кратных частот ω₁ , ω₂ , 2ω_{1 ,} 2ω₂ с амплитудами соответственно , , , и гармоники комбинационных частот: разностной частоты ω_p= ω₁ – ω₂ с амплитудой и суммарной частоты ω_с= ω₁ + ω₂ с амплитудой

1.3. Анализ преобразования гармонического сигнала НЭ при кусочно-линейной аппроксимации ВАХ

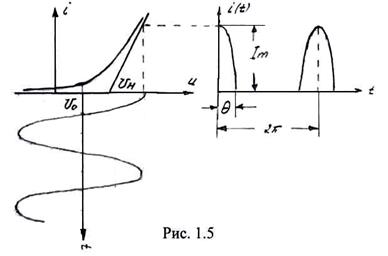При кусочно-линейной аппроксимации вольт-амперная характеристика описывается выражением (1.7). Так же, как и в предыдущем случае, входной сигнал представляет собой сумму напряжения смещения U₀ и гармонического сигнала (выражение 1.8).

На Рис. 1.5 изображена вольт-амперная характеристика, а также графики входного сигнала и тока, протекающего через нелинейный элемент.

Ток, протекающий через НЭ имеет вид периодической последовательности импульсов косинусоидальной формы, ограниченных по амплитуде.

Подстановка (1.8) в (1.7) дает следующее выражение для тока:

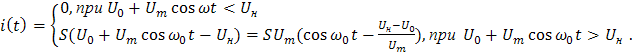(1.15)

Вводится специальный параметр – угол отсечки θ, определяемый из соотношения:

.

Откуда:

. (1.16)

В соответствии с этим величина 2θ равна длительности одного импульса, выраженного в угловой мере, т.е. ωτ_и = 2θ.

Для определения спектрального состава тока необходимо провести разложение периодической последовательности косинусоидальных импульсов в ряд Фурье, которое приводит к следующему результату:

i(t)=I₀+I₁cosω₀t+ I₂cos2ω₀t+…+ I_kcoskω₀t ,

где I₀=SU_mγ₀(θ), I₁=SU_mγ₁(θ), I₂=SU_mγ₂(θ) , … , I_k=SU_mγ_k(θ), - амплитуды соответствующих гармоник,

γ₀(θ), γ₁(θ), γ₂(θ), … , γ_k(θ), – функции Берга.

Значения функций Берга рассчитаны для различный значений K и Θ и сведены в таблицу (табулированы).

Зависимости γ_k(θ) показывают, как изменяется амплитуда к-той гармоники тока, если амплитуда входного сигнала постоянна, а угол отсечки изменяется за счет изменения напряжения смещения .

Для получения наибольшей амплитуды желаемой гармоники тока необходимо обеспечить оптимальный угол отсечки. Так, например для второй гармоники при , оптимальный угол отсечки Θ=90⁰.