Помехоустойчивость связи при передаче непрерывных сообщений будем характеризовать величиной среднеквадратической ошибки 
2, определяемой выражением
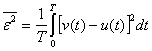(9.1)
Разность [v(t)—u(t)] можно рассматривать как «помеху» на выходе приемника. Если канал имеет идеальную П-образную частотную и линейную фазовую характеристики, то при наличии флуктуационной помехи с равномерным спектром расхождение между v и u на частоте f определяется интенсивностью помехи на выходе приемника на этой частоте G
(f), а среднеквадратическое расхождение за счет всех составляющих равно средней мощности помехи на выходе приемника P. Относительная ошибка будет равна:
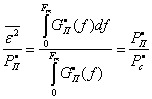
где Fm — полоса пропускания приемника по низкой частоте, P
средняя мощность сообщения на выходе приемника.
Отношение сигнал/помеха в канале, как уже отмечалось, может быть улучшено приемником. Степень улучшения зависит не только от способа приема, но и от способа передачи, в частности, от способа модуляции. Поэтому помехоустойчивость систем связи при передаче непрерывных сообщений удобно оценивать относительным увеличением (выигрышем) отношения сигнала к помехе на выходе приемника по сравнению со значением этого отношения на входе
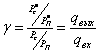(9.2)
где 
и 
—отношения средних мощностей сигнала и помехи соответственно на выходе и входе приемника. При заданном способе передачи 
определяет выигрыш, обеспечиваемый приемником, а при данном способе приема величина характеризует выигрыш, который может быть получен при различных способах передачи.
При сравнительной оценке различных систем связи следует сравнивать на входе и выходе отношения мощностей сигнала не к мощностям помехи, а к их средним спектральным плотностям, т. е. определять «обобщенный выигрыш системы»
(9.3)
где 
Fm '
Определим искажения передаваемых сообщений u(t) при приеме на оптимальный приемник, реализующий условие (5.86). Так как u(t), а значит, и 
2 является функциями параметров 
, то согласно требованиям получения минимума выражения (5.86) частные производные от 2 по должны равняться нулю, т. е.
(9.4)
где обозначено 
Предположим, что сигналы s(u, t) выбраны так, что все 
ортогональны между собой:
и
(9.5)
Пусть под действием помех принятый сигнал x(t) получил приращение 
, тогда получит некоторое приращение 
, а сигнал s(u, t) получит приращение
При этом условие (9.4) запишется в виде
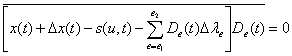
или, принимая во внимание (5.86) и (9.5)
откуда
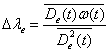(9.6)
При малом уровне помех функция x(t) получает приращение dx(t)=ω(t). При этом параметры получат приращения, равные
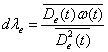(9.7)
Поскольку ω(t) есть случайная величина с нормальным распределением, то и приращения d, .получаемые от действия помехи, также будут случайными величинами, имеющими нормальное распределение с нулевым средним и дисперсией
Величина d характеризует отклонение параметра от переданного значения 
, т. е. ошибку воспроизведения этого параметра 
При малом уровне помех плотность вероятности этой ошибки является нормальной
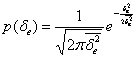
где 
среднеквадратическое значение ошибки.
В телеметрических системах сообщениями являются передаваемые параметры, характеризующие те или иные физические величины (скорость, температуру и т. п.). Потенциальная помехоустойчивость таких систем определяется величиной среднеквадратической ошибки
(9.8)
или вероятностью того, что ошибка по модулю превысит заданную величину 
.
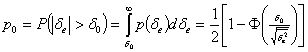
Если в общем случае передавалось непрерывное сообщение
то при отсутствии помех принятый сигнал будет x(t)=s(u,t). По этому сигналу оптимальный приемник воспроизводит переданное сообщение u(t) безискажений: v(t) = u(t).
При наличии помех воспроизводимое оптимальным приемником сообщение
(9.10)
Где 
(9.11)
Здесь 
e — нормальная случайная величина с единичной дисперсией. Так как при отсутствии помех v(t) = u(t)-, то функцию 
*(t) можно рассматривать как составляющую выходного колебания, вызванную помехой на входе, т. е. как колебание помехи на выходе приемника.
Функция ω*(t) есть стационарное флуктуационное колебание с нормальным законом распределения вероятностей. Такая функция полностью характеризуется своим энергетическим спектром. Согласно (9.11) этот спектр определяется следующим выражением:
(9.12)
Интенсивность помехи на выходе приемника, определяемая ф-лой (9.12), является минимально возможной и характеризует потенциальную помехоустойчивость при данной системе модуляции. Из сопоставления ф-л (9.8) и (9.12) следует соотношение
(9.13)
Мощность помехи на выходе приемника с полосой частот от 
до 
будет равна:
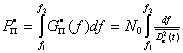(9.14)
Следует помнить, что колебание ω*(t) и мощность P
* определений для u(t), лежащего в пределах ±1. Мощность сигнала (сообщения) на выходе в этих условиях равна: 
,
Где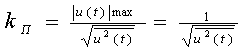 
— пикфактор сообщения.
Поэтому отношение сигнала к помехе на выходе приемника
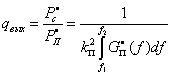(9.15)
В случае, когда u(t) представляет синусоиду, 
и
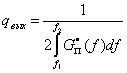
При телефонной передаче речи считают 
Отношение сигнала к помехе на входе приемника соответственно будет равно: 
(9.16)
Обобщенный выигрыш системы γ' согласно (9.3), (9.15) и (9.16) будет определяться следующим выражением:
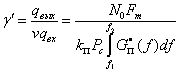(9.17)
Здесь, как и раньше, мы полагаем, что спектр помехи на входе приемника равномерный.
Частотные характеристики приемника считаются идеальными: тракта высокой частоты (до детектора) с полосой пропускания F, а тракта низкой частоты с полосой Fm—f
—f
.
Известные системы модуляции можно разделить на прямые и интегральные. Прямыми называются такие системы, в которых сообщение u(t) входит непосредственно в выражение сигнала. Для этих систем:
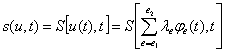(9.18)
и, считая частоту несущей f0 >> F
,
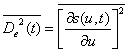
Тогда согласно (9.t2) для прямых систем будем иметь
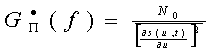
К прямым системам относятся различные виды линейной модуляции (AM, БМ) и фазовая модуляция (ФМ).
Интегральными системами называют системы, в которых сообщение u(t) входит в выражение сигнала под знаком интеграла
(9.20)
где 
.
Для таких систем
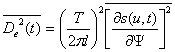и
(9.21)
Это соотношение можно непосредственно получить на основании теоремы о спектре производной.
Из ф-л (9.18) и (9.21) следует, что энергетический спектр помехи на выходе приемника в случае прямых систем модуляции получается равномерным, а в интегральных системах — паpaбoлическим.
Для передачи непрерывных сообщений по каналу связи применяются различные способы модуляции. При синусоидальном переносчике этими способами являются амплитудная модуляция (AM), однополосная модуляция (ОМ), двухполосная амплитудная модуляция с подавленной несущей (БМ), частотная модуляция (ЧМ) и фазовая модуляция (ФМ). Указанные системы модуляции относятся к типу аналоговых систем, в которых один из параметров непрерывного колебания изменяется в соответствии с передаваемым сообщением.
При импульсном способе при передачи непрерывных сообщений в качестве переносчика используется периодическая последовательность импульсов определенной формы. Основными видами модуляции в этом случае является амплитудно-импульсная модуляция (АИМ), широтно-импульсная модуляция (ШИМ), фазоимпульсная модуляция (ФИМ) и частотно-импульсная модуляция (ЧИМ).
При цифровом или кодовом способе передачи наибольшее распространение получили импульсно-кодовая модуляция (ИКМ) и дельта-модуляция (ДМ).
И, наконец, возможно применение различных способов модуляции сложного (шумоподобного) переносчика.