2.1. Волны, частицы и электромагнитный спектр

2.2. Принцип действия волоконных световодов

2.3. Основные положения геометрической (лучевой) оптики при передаче света в волоконных световодах

2.3.1. Основы геометрической оптики

2.3.2. Анализ лучевого распространения света в волоконных световодах

2.4. Основные положения волновой теории передачи света по световодам

2.4.1. Основные понятия

2.4.2. Взаимодействие оптической волны со средой

2.4.3. Волновые уравнения

2.4.4. Граничные условия

2.4.5. Волновой анализ распространения мод

2.4.6. Глоговское группирование мод

2.5. Параметры оптических волокон

2.5.1. Геометрические и оптические параметры оптических волокон

2.5.2. Параметры передачи оптических волокон

2.5.3. Механические параметры оптических волокон

2.1. Волны, частицы и электромагнитный спектр

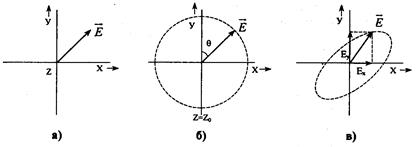
Рис. 2.1. Типы поляризаций: а — линейная; б — круговая; в — эллиптическая

Свет представляет собой один из видов электромагнитной энергии, такой же как радиоволны, рентгеновские лучи и, наконец, электронные цифровые импульсы. Электромагнитные волны— это переменные магнитные и электрические поля, направленные перпендикулярно друг другу и направлению распространения. Световая волна является поперечной волной. Если электрическое и магнитное поля колеблются в плоскости, то в фиксированной точке пространства (Z) конец вектора напряженности электрического или магнитного поля с течением времени перемещается вдоль отрезка прямой линии. Такую волну называют линейно-поляризованной. Если вектор , оставаясь неизменным по величине, вращается с угловой частотой ω вокруг направления Z₀, то конец вектора описывает окружность. Волны такого типа называются волнами с круговой поляризацией. При произвольных значениях амплитудных и начальных фазовых составляющих вектора (E_х, Еу, и φ_х, φ_у) в фиксированной точке пространства Z конец этого вектора описывает эллипс. Волны такого типа принято называть волнами с эллиптической поляризацией (рис 2.1).

В физике все виды материи разделяются либо на волны, либо на частицы. Обычно свет представляется в виде волн, а электроны — в виде частиц. Однако современные физические исследования показали, что четкой границы между частицами и волнами не существует. Поведение как частицы, так и волны может быть и корпускулярным, и волновым.

Частицы света называются фотонами. Фотон представляет собой квант, или пакет излучения. Квант — это элементарная единица излучения. Нельзя наблюдать половину или 5,33 кванта. Количество энергии, переносимое фотоном, увеличивается с ростом частоты: большие частоты соответствуют большему количеству энергии. Длине волны фиолетового диапазона, имеющей большую частоту, соответствует большее количество энергии, чем волнам красного диапазона. Энергия, запасенная в одном фотоне,

E=hf, (2.1) где f — частота и h — постоянная Планка, равная 6,63х10^-34Дж∙с (джоуль секунда).

Из уравнения видно, что энергия фотона пропорциональна частоте (или длине волны).

Существует несколько уровней энергии для различных высокочастотных длин волн и, чем выше частота, тем большую энергию имеет квант.

Инфракрасный свет (10¹³ Гц) 6,63 х10^-20 Дж ∙ с

Видимый свет (10¹⁴ Гц) 6,63 х10^-19 Дж ∙ с

Ультрафиолетовый свет (10¹⁵ Гц) 6,63 х10^-18Дж ∙ с

Рентгеновские лучи (10¹⁸ Гц) 6,63 х10^-15 Дж ∙с

Фотон является странной частицей с нулевой массой покоя. Если он не движется, то не существует. В этом смысле фотон не является частицей, такой как камень или капля чернил. Он служит вместилищем энергии, но ведет себя как частица.

В волоконной оптике свет рассматривают и как частицу, и как волну. Обычно в зависимости от смысла используют либо одно, либо другое понятие. Например, многие характеристики оптического волокна основаны на длине волны, и свет рассматривается как волна. Однако испускание света источником или его поглощение детектором лучше описывается теорией частиц.

Фотоны, попадающие на детектор и поглощаемые им, выделяют энергию и обеспечивают электрический ток в цепи. Светоизлучающие диоды (СИД) работают на принципе передачи энергии от электронов к фотонам, энергия которых определяет длину волны излучаемого света. Таким образом, свет ведет себя различным способом при различных обстоятельствах. Поэтому, чтобы описать свет, необходимо использовать, в зависимости от обстоятельств, различные подходы (положения геометрической оптики, волновой оптики или квантовой оптики) [1].

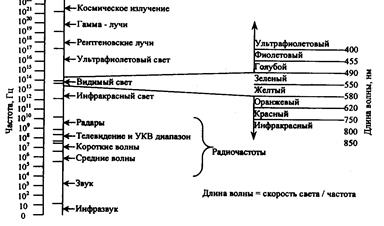Рис. 2.2. Электромагнитный спектр

В данной книге свет рассматривается, как электромагнитная волна или как электромагнитное излучение. Рассмотрим электромагнитный спектр, используемый в волоконных световодах. Электромагнитное излучение образует непрерывный частотный спектр, простирающийся от ультразвука к радиоволнам, микроволновому излучению, рентгеновским лучам и далее (рис. 2.2). Свет представляет собой электромагнитное излучение с большей частотой и более короткой длиной волны по сравнению с радиоволнами. Он распространяется в волне таким же образом, как и радиосигналы, рентгеновские лучи и т.д. Световое излучение занимает только маленькую часть электромагнитного спектра [2].

Видимый свет находится в пределах диапазона волн 390-760 нанометров (нм=10^-9 м), или 0,39-0,76 тысячных частей мм. Сравните это с радиоволнами, которые имеют длину волны от сотен до тысяч метров! Свет в общем использовании означает только видимый свет, но этот термин обычно расширяется и включает и ультрафиолетовое (коротковолновое), и инфракрасное излучение (длинноволновое). Фактически термин свет охватывает весь спектр излучения, который может управляться подобным способом (линзами, сетками, призмами и т.д.). Этот более широкий диапазон находится в пределах от 190 нм (ультрафиолетовый свет) до 2000 нм (инфракрасный свет).

В оптической связи с помощью волоконных световодов используется приграничный с инфракрасным диапазоном волны от 800 до 1600 нм. На данном этапе в волоконно-оптических системах передачи ВОСП в казанном диапазоне применяется пять окон прозрачности (табл. 2.1).

Таблица 2.1. Диапазоны длин волн окон прозрачности

Окно прозрачности	Диапазон длин волн, нм
Первое	Около 850
Второе	1280 – 1325
Третье	1530 – 1565
Четвертое	1565 – 1620
Пятое	1350 - 1450

Высокие частоты света или малые длины волн представляют большой интерес с точки зрения коммуникационной технологии, так как более высокие частоты несущей волны означают большую скорость передачи информации. Технология волоконной оптики позволяет использовать потенциальную возможность света и обеспечивать высокую скорость передачи информации.

2.2. Принцип действия волоконных световодов

Основным элементом волоконно-оптического кабеля (ВОК), или в дальнейшем оптического кабеля (ОК), является волоконный световод (ВС). Волоконный световод, или оптическое волокно (ОВ), — это оптический волновод ВОСП, предназначенный для направленной передачи оптического излучения, выполненный в виде тонкой стеклянной нити цилиндрической формы с круглым поперечным сечением. Оптическое волокно состоит из сердцевины, одной или нескольких оболочек и одного или нескольких защитных покрытий.

Сердцевина ОВ — это центральная область ОВ, через которую передается основная часть оптической мощности сигнала. Среднее значение показателя преломления (ПП) оболочки меньше среднего значения в сердцевине. В ОВ применяются однородные или депрессированные оболочки. У однородных оболочек ОВ значение ПП постоянное, у депрессированных переменное. Диэлектрическим материалом для сердцевины и оболочки ОВ служит плавленый кварц (кварцевое стекло), чистый или с примесями химических элементов и их соединений, небольшие пропорции которых способствуют изменению оптических свойств плавленого кварца должным образом. Плавленный кварц — это аморфное, прозрачное вещество с химической формулой двуокиси кремния SiO₂. Сердцевина и оболочка ОВ обладают разными оптическими характеристиками (показателями преломления n₁ и n₂). Если сердцевина служит для передачи электромагнитной энергии, то оболочка — для создания лучших условий отражения на границе раздела сердцевина — оболочка, защиты сердцевины волокна от механических повреждений, а также для защиты от излучения энергии в окружающее пространство и поглощения нежелательного излучения извне.

Волоконные световоды делятся на две группы: многомодовые и одномодовые. В конструктивном отношении они различаются диаметром сердцевины (рис. 2.3). В одномодовом световоде диаметр сердцевины d₁ соизмерим с длиной волны (d₁≈λ), и по нему передается лишь один тип волны (моды). В многомодовых световодах диаметр сердцевины d₂ больше длины волны (d₂>λ), и по нему распространяется большое число волн. Практически диаметр сердцевины световода составляет 6 — 8 мкм у одномодовых и 50 мкм у многомодовых световодов, диаметр оболочки — 125 мкм, диаметр волокна по защитному покрытию — 250 мкм.

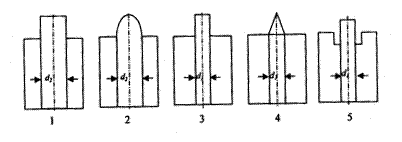
Рис. 2.3. Профили показателей преломления различных световодов:

многомодовых: 1 – ступенчатого, 2 – градиентный;

одномодовых: 3 – ступенчатого, 4 – треугольного, 5 – типа W

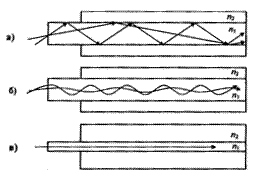
Рис. 2.4. Волоконные световоды: а – ступенчатые многомодовые; б – градиентные многомодовые; в - одномодовые

Профили показателей преломления (ППП) различных ОВ приведены на рис. 2.3. ППП многомодовых ОВ подразделяются на ступенчатые и градиентные. В ступенчатых ВС показатель преломления в сердцевине постоянен и имеется резкий переход от n₁ сердцевины к n₂ оболочки. Градиентные ВС имеют непрерывное плавное изменение показателя преломления в сердцевине по радиусу световода от центра к периферии.

В одномодовых ОВ ППП, в свою очередь, подразделяется на ступенчатый, треугольный, типа W (рис. 2.3).

Траектории лучей в световодах различных групп представлены на рис. 2.4. В ступенчатом многомодовом световоде лучи резко отражаются от границы сердцевина–оболочка. При этом пути следования различных лучей различны, и поэтому они приходят к концу линии со сдвигом во времени, что приводит к искажению передаваемого сигнала (дисперсии). В градиентных световодах лучи распространяются по волнообразным траекториям, поэтому искажений меньше. В наилучших условиях находится одномодовая передача, так как здесь распространяется лишь один луч.

Математически профиль показателя преломления (ППП) ОВ может быть описан выражением вида:

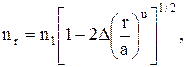(2.2)

где n₁ — максимальное значение ППП на оси волокна, т.е. при r=0; а — радиус сердцевины; u — показатель степени, описывающий изменение ППП; ∆ — относительная разность показателей преломления сердцевины и оболочки ОВ. В разных волокнах значение ∆ меняется от 0,003 до 0,01.

Показатель степени для треугольного профиля ПП равен 1, параболического — 2, а прямоугольного (ступенчатого) — ∞.

Физические процессы, происходящие при распространении электромагнитных волн в волоконных световодах оптических кабелей, имеют свои особенности. В отличие от обычных кабелей, обладающих электрической проводимостью и током проводимости I_пр, ОК имеют совершенно другой механизм передачи, а именно: токи смещения I_см на основе которых действует также радиопередача. Однако волна в ОК распространяется не в свободном пространстве, а концентрируется в самом объеме световода и передается по нему в заданном направлении (рис. 2.5).

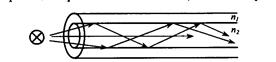
Рис. 2.5. Процесс передачи волны по световоду

Например, передача волны по световоду со ступенчатым профилем показателя преломления осуществляется за счет отражений ее от границы сердечника и оболочки, имеющих разные показатели преломления (n₁ и n₂).

В обычных кабелях носителем пере даваемой информации является электрический ток, а в ОК — лазерный луч.

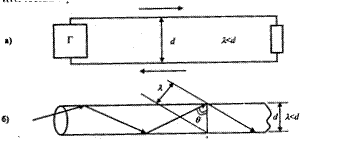
Рис. 2.6. Передача по направляющим схемам: а – двухпроводной; б - волноводной

В симметричных и коаксиальных кабелях передача осуществляется по двухпроводной схеме с применением прямого и обратного проводника цепи. В световодах, волноводах и некоторых других направляющих системах нет двух проводников, и передача происходит волноводным методом за счет многократного отражения волны от границы раздела сред (рис. 2.6). Такой отражающей границей может быть металл — диэлектрик, диэлектрик — диэлектрик с различными диэлектрическими (оптическими) свойствами и др. На волноводном принципе действуют световод, волновод, линия поверхностной волны, диэлектрический волновод и другие конструкции направляющих систем.

Граница раздела разных направляющих систем характеризуется соотношением между длиной волны λ и поперечными размерами направляющей системы d. При λ > d требуется два провода: прямой и обратный и передача происходит по обычной двухпроводной схеме. При λ < d не требуется двухпроводной схемы и передача происходит за счет многократного зигзагообразного отражения волны от границ раздела сред с различными характеристиками. Поэтому передача по волноводным системам (световодам, волноводам и другим НС) возможна лишь при частотах, у которых длина волны соизмерима или меньше, чем поперечные размеры — диаметр НС.

Рассмотрим принцип действия волоконного световода и возможные случаи распространения волны в световоде для разных частот [1.3]. На рис. 2.7 показаны предельные случаи распространения малых длин волн при λ →0 (рис. 2.7 а) и волн, соизмеримых с диаметром световода (d) при λ →d (рис. 2.7 б). В первом случае отражений мало и волна стремится к прямолинейному движению вдоль световода, т.е. передача проходит в выгодных условиях.

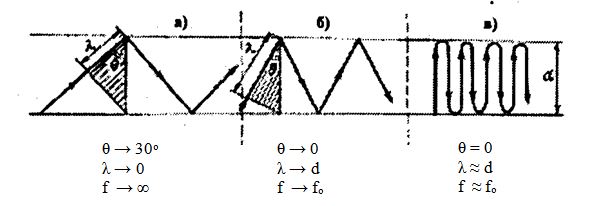
Рис. 2.7. Распространение волн в световоде для частот:

а – очень высоких; б – менее высоких; в - критических

Во втором случае волна часто отражается и поступательное движение ее весьма мало. В этом случае вдоль световода передается незначительная доля энергии.

При определенной длине волны λ≈d (рис. 2.7 в) -наступает такой режим, когда θ = 0, волна падает на оболочку световода и отражается перпендикулярно. В световоде устанавливается режим стоячей волны, и энергия вдоль световода не перемещается. Этот режим соответствует критической длине волны λ₀ =d и критической частоте f₀=c/d.

Таким образом, в световоде могут распространяться лишь волны длиной меньшей, чем диаметр сердцевины световода (λ<d). С учетом того, что, например, в световоде со ступенчатым ППП границей раздела сердцевина — оболочка являются прозрачные стекла, возможно не только отражение оптического луча, но и проникновение его в оболочку. Для предотвращения перехода энергии в оболочку и излучения в окружающее пространство необходимо соблюдать условия полного внутреннего отражения. Реализация этого условия применительно к двухслойному световоду показана на рис. 2.8.

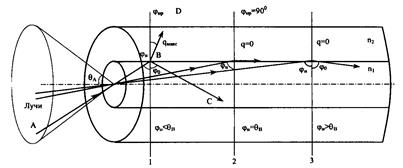
Рис. 2.8. Принцип действия волоконного световода:

1 — имеется преломленный луч; 2 и 3- отсутствует преломленный луч

По законам геометрической оптики на границе сердцевина — оболочка будут находиться падающая волна АВ с углом φ_n, отраженная ВС с углом φ_o, и преломленная волна BD с углом φ_np (рис. 2.8, линия 1). Известно, что при переходе из среды с большей плотностью в среду с меньшей плотностью, т.е. при n₁>n₂, волна при определенном угле падения полностью отражается и не переходит в другую среду. Угол падения, начиная с которого вся энергия отражается от границы раздела сред, т.е. φ_n=θ_в, называется углом полного внутреннего отражения. Этот угол определяется из соотношения:

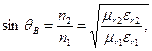(2.3)

где μ_r1 и ε_r1, μ_r2 и ε_r2 — магнитная и диэлектрическая проницаемости сердцевины и оболочки.

При критическом угле φ_n=θ_в волна движется вдоль границы раздела сред сердцевина — оболочка (рис. 2.8, линия 2) и нет излучения в окружающее пространство. При φ_n>θ_в волна полностью отражается и возвращается в исходную среду — сердцевину (рис. 2.8, линия 3). Излучения также нет. Чем больше угол падения волны, т.е. φ_n>θ_в в пределах от q_в до 90^о, тем лучше условия распространения и быстрее волна придет к приемному концу. В этом случае вся энергия концентрируется в сердцевине световода и практически не излучается во внешнюю среду. При угле, меньшем угла полного отражения, т.е. при φ_n < θ_в, энергия проникает в оболочку, излучается во внешнее пространство и передача по световоду неэффективна.

Режим полного внутреннего отражения предопределяет условие ввода света во входной торец волоконного световода. Как видно из рис. 2.8 световод пропускает лишь свет, заключенный в пределах телесного угла θ_А, который обусловлен углом полного внутреннего отражения θ_в.

2.3. Основные положения геометрической (лучевой) оптики при передаче света в волоконных световодах

2.3.1. Основы геометрической оптики

Геометрическая оптика имеет историю, датируемую двумя тысячами лет, и предполагает, что свет состоит из лучей, распространяющихся от источника по прямым линиям в гомогенной среде, например стекле, воде, воздухе или вакууме. При этом в геометрической оптике принято утверждение, что плоские волновые фронты распространяются под прямыми углами к каждому лучу и свет уменьшается пропорционально квадрату расстояния.

В общем случае под скоростью света понимают скорость электромагнитной энергии в вакууме. В других материалах (например, в стекле) свет распространяется с меньшей скоростью. При перемещении из одного материала в другой изменяется скорость распространения, что, с точки зрения волновой теории, приводит к изменению направления движения. Отклонение света от прямого направления называется преломлением. Волны с различными длинами в одном и том же материале распространяются с различными скоростями. Зависимость скорости от длины волны имеет важное значение в волоконной оптике.

Как известно, луч света при падении на границу раздела двух сред делится на отраженный и преломленный. Согласно закону отражения луч света, который падает на границу раздела двух сред, отражается под тем же самым углом (φ_отр) к нормали (перпендикуляру к границе), что и угол падения (φ_n) к поверхности, т.е. φ_n = φ_отр .

Согласно закону Снеллиуса (закон преломления) лучи света, падающие на границу раздела двух сред, имеют углы преломления, отличные от углов падения к нормали границы этих сред. Связь этих углов определяется выражением:

n₁sin φ_1п=n₂sin φ_1пр , (2.4)

где n₁ и n₂ — показатели преломления первой и второй сред, соответственно.

Показатели преломления n (величина безразмерная) выражается через отношение скорости света в вакууме (с) к скорости света в материале (v):

(2.5)

Показатели преломления различных веществ и скорости распространения света в них [2] приведены в табл. 2.2.

Таблица 2.2. Показатели преломления различных материалов

Особый интерес для волоконной оптики представляет тот факт, что показатель преломления стекла может из меняться в зависимости от его состава. Количество отраженного света от границы двух сред зависит от их показателей преломления. Если излучение видимой области спектра падает на границу раздела двух сред и переходит из оптически более плотной среды n₁на оптически менее плотную n₂ (n₂< n₁) и угол падения увеличивается, то угол преломления приближается к 90^о. Увеличивая угол падения, можно добиться такого состояния, при котором преломленный луч будет располагаться вдоль границы раздела сред, не переходя в другую среду.

Угол падения при этом называется критическим углом (φ_кр) полного внутреннего отражения, т.е. угол падения, при котором угол преломления равен 90^о, называется критическим углом. Если угол падения больше критического, то свет полностью отражается в исходную среду, не проникая в другой материал. При этом имеет место только отражение, а преломление отсутствует, что приводит к полному внутреннему отражению, т.е. при φ_1пр =90^о

(2.6)

На этом явлении основан принцип передачи оптического излучения по волоконным световодам.

Рассмотрим отражение света при угле падения, равном 90^о. Даже когда свет проходит в более плотную среду, некоторая его часть отражается в исходную среду. Этот эффект получил название отражение Френеля. Чем больше разница показателей преломления сред, тем большая доля света отражается назад. Показатель Френелевского отражения на границе с воздухом

(2.7)

В децибелах потери переданного света составляют:

А = 10lg(1- р). (2.8)

Примером последствий отражения Френеля могут служить потери на вводе и выводе оптического излучения в волоконный световод.

Для света, падающего из воздуха на границу стекла (с n=l,5 для стекла), потери от френелевского отражения равны примерно 0,17 дБ. Это значение зависит от состава стекла. Поскольку такого рода потери происходят как при входе света в стекло, так и при выходе из него, то потери на соединении двух стекол составляют 0,34 дБ.

Поляризованный свет. Свет может рассматриваться как волна, состоящая из двух полей, направленных перпендикулярно друг к другу: электрического поля и магнитного поля (рис. 2.9). Эти поля синхронны с полевыми векторами, с разностью фаз между собой в 90^о.

Нормальный свет имеет бесконечное число перпендикулярно колеблющихся плоскостей, распространяющихся в направлении перемещения света. Отражением и рефракцией свет может быть поляризован.

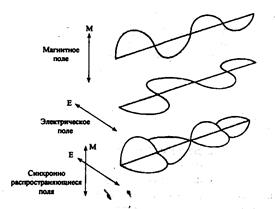
Рис. 2.9. Поля, составляющие свет: электрическое и магнитное

Свет, в котором интенсивность электрического поля остается неизменной, в то время как интенсивность магнитного поля уменьшается, назван ТЕ-поляризованным светом (коэффициент пропускания электрически поляризованного света). Свет, в котором интенсивность магнитного поля остается неизменной, в то время как интенсивность электрического поля уменьшается, называется ТМ-поляризованным светом (коэффициент пропускания поляризованного магнитного поля).

На рис. 2.10 показан пример поляризации света, падающего на поверхность некоторой кристаллической пластины, при этом электрическое и магнитное поля поляризуются по-разному.

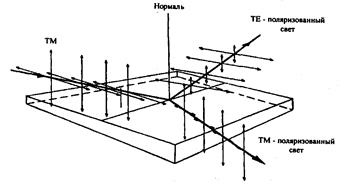
Рис. 2.10. Разложение падающего света с помощью пластины на поляризованные электрическое и магнитное поля

Два типа поляризации имеют несколько разные коэффициенты отражения, которые описываются законом отражения Френеля. Интенсивность отраженного света увеличивается от 4 % до 100 % при увеличении угла падения от 0 до 90^о для обеих поляризаций (преломленный свет уменьшается на эту же степень), но для ТМ-поляризации интенсивность сначала уменьшается с 4% до нуля, а затем снова увеличивается до 100 % (рис. 2.11). Угол, при котором ТМ-отражение является нулевым, называется углом Брюстера.

Принцип распространения света в стекловолокне основан на законе полного внутреннего отражения. При типичных значениях ПП в сердцевине n₁=1,47 и оболочке n₂=1,46 ОВ со ступенчатым ППП имеет критический угол полного внутреннего отражения φ_кр=83,3^о.

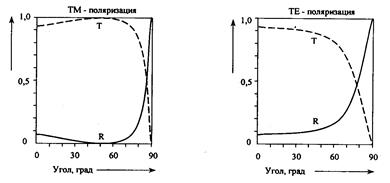
Рис. 2.11. Диаграммы зависимости коэффициентов отражения (R) и преломления (Т) различных поляризаций от угла падения света

Рис. 2.12. Рэлеевское рассеяние света из-за примесей в среде передачи

Рэлеевское рассеяние и свет Тиндаля. В аморфном материале типа стекла структура материала не везде однородна, поэтому стекло никогда полностью не будет прозрачно. Световой луч, распространяющийся через такой материал, рассеивается в направлениях (например, луч солнечного света в пыльном или заполненном дымом помещении) (рис. 2.12). Это явление называется рэлеевским рассеянием и вызвано присутствием в среде маленьких частиц и неоднородностей. Рассеянный свет называется светом Тиндаля. Гидроксильная группа (ОН^--), ионы металлов, примеси и т.д. объясняют это явление в стекловолокне.

Рэлеевское рассеивание — это то, что дает небу его синий цвет и солнцу его красный цвет на восходе и на закате. Эти цветные явления вызваны рассеиванием света молекулами воздуха. Молекулы и вариации неоднородностей в стекле функционируют как электрические диполь, излучающие поле.

В атмосфере коротковолновый свет (синий конец спектра) рассеивается в 3-4 раза больше, чем длинноволновый свет (красный конец спектра), который придает небу различные цвета в зависимости от положения солнца на небе. Лорд Рэлей объяснил это явление и показал, что рассеяние имеет решающее значение в выборе диапазона волн в волоконной оптике. Чем больше длина волны, тем меньше потери от рэлеевского рассеяния.

2.3.2. Анализ лучевого распространения света в волоконных световодах

В геометрической оптике световые волны изображаются лучами, направленными по нормали к волновой поверхности. При падении световой волны на плоскую границу раздела двух диэлектриков с разными значениями относительной диэлектрической проницаемости (ε) в общем случае наблюдаются прошедшая (преломленная) и отраженная волны. В соответствии с законом Снеллиуса угол падения связан с углами отражения и преломления с помощью равенства φ_п= φ_отр и выражения (2.4). Поскольку в оптических средах отношение магнитной проницаемости (μ) к магнитной проницаемости вакуума (μ₀) принимается равным единице, то в этом выражении а . В ОВ среда сердцевины более плотная, чем среда оболочки, т.е. n₁>n₂, поэтому при угле падения φ_п> φ_кр свет полностью отражается от границы сердцевина — оболочка и распространяется только в сердцевине волокна. Как известно, критический угол падения света определяется выражением:

(2.9)

Поток энергии из первой среды во вторую в среднем равен нулю, и энергия падающей электромагнитной волны полностью возвращается в первую среду.

В качестве примера рассмотрим ОВ со ступенчатым профилем показателя преломления. Ступенчатое оптическое волокно (рис. 2.13) представляет собой двухслойную стеклянную нить, сердцевина которой изготовлена из стекла с показателем преломления n₁ диаметром 2a=(3...50) мкм, а оболочка имеет показатель преломления n₂ и диаметр 2b=125 мкм. Для обеспечения полного внутреннего отражения на границе раздела необходимо, чтобы n₁>n₂. Поверх оболочки накладывается защитное покрытие с показателем преломления n₃< n₂.

На рис. 2.13 световые лучи, описывающие однородные плоские волны, пучком исходят от точечного источника, расположенного на оси волокна. На торце ОВ этот пучок лучей преобразуется в два типа лучей волокна: меридиональные, которые пересекают ось волокна, и косые, которые не пересекают эту ось. На рис. 2.14 представлена траектория прохождения косого луча в ступенчатом ОВ.

Часть меридиональных и косых лучей, испытывая полное внутреннее отражение в местах падения на границу сердцевина — оболочка, распространяется зигзагообразно вдоль ОВ.

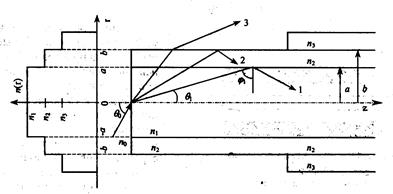
Рис. 2.13. Модель ОВ со ступенчатым профилем показателя преломления

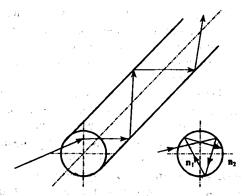
Рис. 2.14. Траектория прохождения косого луча в ОВ

Рассмотрим ход меридиональных лучей, падающих на входной торец ОВ и распространяю- щихся затем вдоль волокна (рис. 2.13). В зависимости от угла наклона луча θ₁ к оси Z меридиональные лучи, лежащие в плоскости рисунка, могут испытывать полное внутреннее отражение на границе сердечник — оболочка, если θ₁<arccos(n₂/n₁). При этом образуются моды сердечника 1, или направляемые моды. Если луч падает под углом arccos(n₂/n₁)< θ₁< arccos(n₃/n₂), то он может сформировать моду оболочки 2. Световые лучи, падающие под углом θ₁< arccos(n₃/n₂), излучаются в пространство, т.е. в защитную оболочку, образуя вытекающие моды, или моды излучения 3.

Луч, падающий на торец волокна из окружающей среды под углом θ₀ к оси волокна, преломляется при вхождении в сердцевину и распространяется в ней под углом θ₁ в соответствии с законом Снеллиуса:

(2.10)

При этом преломленный луч падает на боковую поверхность под углом φ₁=(π/2) – θ₁. Для полного внутреннего отражения лучей от боковой поверхности необходимо, чтобы φ₁≥φ_кр, где критический угол падения φ_кр определяется выражением (2.9). Следовательно, sinφ₁=cosθ₁≥n₂/n₁.

Из (2.10) следует, что

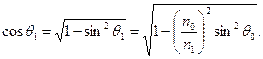
Таким образом,

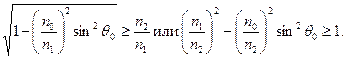
Однако , т.е.

(2.11)

Таким образом, если выполняется условие (2.11), то любой меридиональный луч распространяется вдоль сердцевины волокна. Это условие справедливо и для косых лучей.

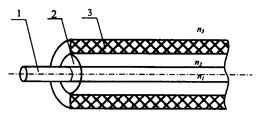
Рис. 2.15. Оптическое волокно: 1-сердцевина; 2-оболочка; 3-защитное покрытие

На рис. 2.15 представлена конструкция волокна в оболочке с защитным покрытием, в котором оптическое излучение распространяется в ОВ такой конструкции при выполнении условия n₁>n₂>n₃.. Соотношение между n₁ и n₂принято характеризовать относительной разностью ПП [4]

(2.12)

которая для большинства ОВ составляет 10^-2...10^-3. Показатель преломления оболочки имеет постоянное значение, а сердцевины — либо постоянное, либо изменяющееся по радиусу по определенному закону.

Изменение показателя преломления ОВ вдоль радиуса называется профилем показателя преломления.

Наличие оптической оболочки усложняет волновой процесс в ОВ. Часть меридиональных и косых лучей, многократно отражаясь от границы сердцевина — оболочка, распространяется вдоль сердцевины и образует моды сердцевины (направляемые моды). Остальные лучи, которые падают на эту границу под углами φ_п<φ_кр, уходят из сердцевины наружу. Лучи, покинувшие сердцевину, образуют моды излучения. Некоторые из них распространяются в оболочке за счет полного внутреннего отражения от границы оболочка — окружающая среда и образуют моды оболочки. Если защитное покрытие ОВ выполнено из сильно поглощающего материала, то оно устраняет перекрестные помехи между ОВ в оптическом кабеле, обусловленные модами излучения. Кроме того, защитное покрытие рассеивает энергию мод оболочки аналогично направляемым модам диэлектрического стержня. Как отмечалось выше, поле направляемых мод частично проникает в окружающую среду, где экспоненциально убывает, при этом глубина проникновения в оболочку ОВ, т.е. расстояние, на котором это поле убывает в е раз (е=2,718), определяется при φ_п>φ_кр выражением [5]:

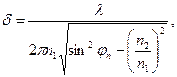(2.13)

где λ — длина волны оптического излучения, вводимого в ОВ.

Режим полного внутреннего отражения предопределяет условие подачи света на входной торец волоконного световода. Из рис. 2.16 видно, что световод пропускает лишь свет, заключенный в пределах телесного угла θ_А, величина которого обусловлена углом полного внутреннего отражения θ_В. Этот телесный угол θ_А характеризуется апертурой. Апертура-это угол между оптической осью и одной из образующих светового конуса, попадающего в торец волоконного световода, при котором выполняется условие полного внутреннего отражения. Обычно пользуются понятием числовой апертуры:

(2.14)

где n₀, n₁, n₂ — показатели преломления воздуха, сердечника, оболочки соответственно.

Имея в виду, что для воздуха n₀=1, получим

(2.15)

Как видно из рис. 2.16 между углом полного внутреннего отражения θ_В и апертурным углом падения луча θ_А имеется взаимосвязь. Чем больше угол θ_В, тем меньше апертура волокна θ_А. Для ступенчатых ОВ, используемых в системах связи, числовая апертура обычно равна 0,18 — 0,23.

Формула (2.15) учитывает только меридиональные лучи ОВ. Однако, в основном, в ОВ преобладают косые лучи, которые не пересекают ось, а распространяются по ломаным (для ступенчатого ОВ) или право- или левовинтовым спиралям (для градиентного ОВ).

Вывод простого выражения для числовой апертуры косых лучей очень сложен. Отметим только, что числовая апертура, подсчитанная для меридиональных лучей ступенчатого ОВ (2.15), меньше действительной числовой апертуры NA_Д, учитывающей все лучи. Отношение NA_Д /NA для различных значений ПП п₁и п₂, например в [5, 6], увеличивается с уменьшением разности п₁-п₂, т.е. с уменьшением апертуры NA меридиональных лучей.

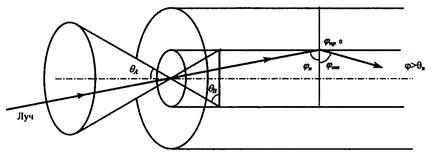
Рис. 2.16. Принцип действия ОВ

Простое и наглядное представление направляемых мод в ОВ с помощью лучей не учитывает свойства света как электромагнитной волны и во многих случаях не позволяет получить правильные результаты. Например, в соответствии с изложенным выше вся бесконечная совокупность лучей, падающих на торец ОВ в пределах угла θ_А, должна образовывать также бесконечную совокупность направляемых мод. Однако это не так. Волновая теория света показывает, что только конечное число лучей конического пучка с определенными углами падения на торец может образовать направляемые моды ОВ. Это объясняется с точки зрения лучевой оптики в ступенчатом световоде тем, что при полном внутреннем отражении от границы с оболочкой волна приобретает фазовый сдвиг, зависящий от угла падения. Если в сердцевине многократно отраженные волны складываются по фазе, то образуется направляемая волна. В противном случае поля волн взаимно компенсируются.

2.4. Основные положения волновой теории передачи света по световодам

2.4.1. Основные понятия

Строгое решение задач распространения электромагнитной энергии по оптическим кабелям требует применения классической электродинамики и уравнений Максвелла. На основе электродинамики можно рассмотреть практически все вопросы передачи, излучения, влияния и поглощения в ОК. Правда, во многих случаях очень сложно искать точные решения на базе электродинамики. Для практики в свое время были разработаны приближенные методы решения задач различных классов. Таким наиболее характерным методом является метод теории геометрической оптики, когда (квазиоптический режим) совершается переход от волновых электродинамических процессов к лучевым процессам (λ→0). При λ→0 области очень высоких частот (свыше 10¹³ Гц) справедливы уравнения геометрической оптики. Однако квазиоптический режим передачи по ОВ является предельным случаем строгих уравнений электродинамики.

Носителем электромагнитной энергии, широко используемой в современной радиоэлектронике, электросвязи и высоковольтной технике, является электромагнитное поле. Электромагнитное поле — это особый вид материи, оказывающий силовое воздействие на заряженные частицы и обладающий энергией, массой, скоростью, т.е. всеми свойствами материи. Поле отличается непрерывным распределением в пространстве (электромагнитные волны) и обнаруживает дискретность структуры (фотоны). Электромагнитное поле представляет собой единство двух составляющих — электрического и магнитного полей. Электрическое поле (Е) характеризуется силовым взаимодействием как с неподвижными, так и с движущимися зарядами. Магнитное поле (Н) характеризуется силовым взаимодействием лишь с движущимися зарядами. Электрические и магнитные поля связаны с определенными количествами электромагнитной энергии. В различных случаях может преобладать тот или иной вид энергии (электрической или магнитной).

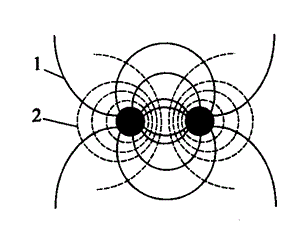
Рис. 2.17. Линии полей: 1-потенциальные; 2-вихревые

Различают два основных типа полей: потенциальное и вихревое. Потенциальное поле тесно связано со своим источником. Линии поля имеют начало и конец. Линии вихревого поля замыкаются по соленоиду, всегда непрерывны и не имеют начала и конца (рис. 2.17). Электростатическое поле является чисто потенциальным, а магнитное — чисто вихревым. Переменное электромагнитное поле в общем случае является суперпозицией потенциального поля электрических зарядов и вихревого поля индукции.

Электрические и магнитные свойства среды характеризуются тремя параметрами: диэлектрической проницаемостью (ε), магнитной проницаемостью (μ) и электрической проводимостью (σ).

Оптическая мощность сигнала, передаваемая по ОВ, описывается векторами напряженности (E ) и индукции (D ) электрического поля, а также векторами напряженности (Н) и индукции (В) магнитного поля. Последние связаны между собой и параметрами среды распространения следующими уравнениями Максвелла, при условии, что проводимость среды σ = 0:

(2.16)

(2.17)

(2.18)

(2.19)

(2.20)

(2.21)

Диэлектрическая и магнитная проницаемости описывают материалы, используемые в ВОСП, которые могут быть линейными и нелинейными, изотропными и анизотропными, однородными и неоднородными, дисперсионными и недисперсионными. У абсолютного большинства материалов, используемых в ВОСП, μ=μ₀ - магнитная проницаемость вакуума.

В зависимости от свойств параметров ε, μ и σ различают следующие среды:

• линейные, в которых параметры ε, μ и σ не зависят от величины электрического и магнитного полей;
• нелинейные, в которых параметры ε, μ и σ (или хотя бы один из них) зависят от величины электрического или магнитного полей.

Все реальные среды, по существу, являются нелинейными. Однако при не очень сильных полях во многих случаях можно пренебречь зависимостью с, и и ч от величины электрического и магнитного полей и считать, что рассматриваемая среда линейна.(В дальнейшем будут рассматриваться только линейные среды.) Линейные среды делятся на однородные и неоднородные, изотропные и анизотропные.

Однородными называют среды, параметры ε, μ и σ которых не зависят от координат, т.е. свойства среды одинаковы во всех ее точках. Среды, у которых хотя бы один из параметров ε, μ или σ является функцией координат, называют неоднородными. Несмотря на то, что кварц является однородной средой, оптическое волокно неоднородно из-за того, что показатели преломления сердцевины и оболочки различны. Поэтому области сердцевины и оболочки в волокне со ступенчато изменяющимся показателем преломления могут рассматриваться раздельно как однородные среды, в то время как в градиентном волокне это допущение неприемлемо, ввиду его неоднородной сердцевины.

Если свойства среды одинаковы по разным направлениям, то среду называют изотропной. Соответственно среды, свойства которых различны по разным направлениям, называют анизотропными. В изотропных средах вектор электрической поляризации ( р) и вектор (E), векторы (D) и (Е), а также векторы магнитной поляризации (М) и (Н), векторы (В ) и (Н ) параллельны, в анизотропных средах они могут быть непараллельными. В изотропных средах параметры ε, μ и σ — скалярные величины. В анизотропных средах, по крайней мере, один из этих параметров является тензором.

В кристаллическом диэлектрике тензором является диэлектрическая проницаемость ε. В общем случае ее записывают в виде матрицы:

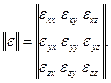
(2.22)

При этом форма уравнения (2.18) остается прежней:

(2.23)

Для того чтобы записать уравнение (2.23) в проекциях на оси прямоугольной системы координат х, у, z, нужно раскрыть правую часть уравнения (2.23) по обычным правилам умножения матрицы. В результате получим

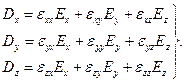(2.24)

Непараллельность векторов D и Е (а также р и Е) в анизотропной среде объясняется тем, что в общем случае направление возникающего в результате поляризации анизотропной среды вторичного электрического поля, созданного связанными зарядами вещества, составляет некоторый угол (отличной от 0 и π) с направлением первичного электрического поля.

Таким образом, в изотропной среде электромагнитные свойства, такие как показатель преломления, одинаковы во всех направлениях, а Е и р являются векторами одинаковой ориентации, и так как кварц представляет собой изотропную среду, идеально цилиндрическое оптическое волокно также является изотропным.

Среда, показатели преломления которой вдоль двух разных направлений соответствующей системы координат, например вдоль осей х и у, различны, называется двулучепреломляющей, поэтому оптическое волокно, не обладающее цилиндрической системой, также является двулучепреломляющим. Двулучепреломление ряда материалов, например ниобата лития, используется в таких волоконно-оптических компонентах, как модуляторы, изоляторы и настраиваемые фильтры.

Среда, в которой ε=const, т.е. однородная по координатам пространства и не зависящая от частоты, называется однородной недисперсионной средой. В ней все частотные составляющие сигнала распространяются с одной и той же фазовой скоростью. Следовательно, сигнал не претерпевает дисперсии. Большинство оптических сред характеризуется тем, что ε = ε (ω) и ν= ν(ω) являются функциями от частоты. Это значит, что косинусоидальные волны

(2.25)

разных частот распространяются с различными фазовыми скоростями, что приводит к расширению сигнала, т.е. к появлению дисперсии.

В выражении (2.25): А — амплитуда волны; ω — круговая частота; n — единичный вектор, нормальный к плоскости, в которой находится плоская волна; r — координата точки наблюдения.

2.4.2. Взаимодействие оптической волны со средой

До сих пор мы говорили о средах без учета распространения в них света, представляющего собой электромагнитную волну. Что происходит, когда оптическая волна распространяется в изотропной среде (материале)?

Как известно, электроны в атоме заряжены отрицательно, а ядро несет положительный заряд. Электрическое поле синусоидальной оптической волны, распространяющейся через материал, воздействует на него. Под действием силы внешнего электрического поля в материале изменяются колебания заряженных частиц атома. В результате такого взаимодействия мощность световой волны уменьшается, т.е. происходит поглощение света. Колеблющиеся заряды атома переизлучают полученную от световой волны мощность на собственных частотах ω₀. Таким образом, синусоидальная оптическая волна частотой в создает систему осцилляторов (диполей). Средняя во времени излучаемая осциллятором мощность в соответствии с законом Рэлея [7] представляется в виде:

(2.26)

где q — заряд частицы, колеблющейся по синусоидальному закону с частотой ω, с — скорость света в вакууме; ε — диэлектрическая проницаемость среды (материала);

Комплексная амплитуда вынужденных колебаний частицы с частотой ω

(2.27)

где m, a, ω₀ — соответственно масса покоя, коэффициент «трения» и резонансная частота частицы.

Поэтому при взаимодействии оптического поля со средой возникают электрические диполь. На микроскопическом уровне плотность дипольных моментов характеризуется вектором поляризации среды. Если в единице объема имеется N одинаковых атомов, каждый из которых содержит, например, η электронов, то вектор поляризации

(2.28)

Таким образом, индуцированная электрическая поляризация материала, или просто поляризация, может быть описана при помощи вектора р, который зависит как от особенностей материала, так и от прилагаемого поля. Индуцированная поляризация рассматривается как отклик среды на прилагаемое электрическое поле. Рассмотрим связь р и Е более подробно, определив вначале вектор D, называемый электрической индукцией:

(2.29)

где ε_ст — постоянная, называемая статической диэлектрической проницаемостью среды, в нашем случае ОВ.

Исходя из (2.28) и (2.29), комплексную диэлектрическую проницаемость можно представить в виде суммы статической и динамической составляющих:

(2.30)

Откуда

(2.31)

Для чистого стекла (плавленого кварца без примесей, химическая формула которого SiO₂) резонансная частота электрона ω₀ расположена в ультрафиолетовой области спектра.

Следовательно, в видимой и ближней инфракрасной областях спектра (ω<<ω₀) диэлектрическая проницаемость практически постоянна:

(2.32)

В реальных стеклах, кроме атомов Si и О, в единице объема содержатся и ионы примесей (ионы — ОН, Fe, Cu, Cr и др.), а также молекулы. Таким образом, для реального стекла в выражение (2.31) необходимо добавить столько членов вида второго члена, сколько имеется диполей, обусловленных примесями. Молекула массивна, поэтому ее ω₀ находится вне спектра частот, используемого в ВОСП. Связь р и E в оптическом волокне определяется свойствами среды (кварца) и является причиной двух важных явлений, относящихся к распространению в нем света, — дисперсии и нелинейным эффектам, которые налагают ограничения на функционирование современных систем ВОСП.

2.4.3. Волновые уравнения

Для математического анализа распространения электромагнитных волн в диэлектрических волноводах (оптических волокнах) методом волновой оптики необходимо воспользоваться уравнениями Максвелла (2.16) — (2.21). Из этих уравнений можно получить более удобное для практики уравнение, взяв операцию ротора от уравнения (2.17) с учетом (2.19),

(2.33)

Подставив (2.16) и (2.18) в (2.33), получим уравнение, содержащее только один вектор Е:

(2.34)

Это уравнение справедливо и в том случае, когда ε изменяется в пространстве, т.е. для неоднородной среды. Первый член выражения (2.34), исходя из векторной алгебры, можно представить в виде:

, (2.35)

где — оператор Лапласа.

Заменив в этом уравнении вектор Е на D/ε, можно получить выражение первого члена правой части в виде:

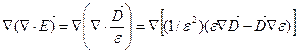. (2.36)

Поскольку то

(2.37)

Тогда с учетом (2.35), (2.36) и (2.37) уравнение (2.34) принимает вид:

(2.38)

Аналогично можно получить волновое уравнение для вектора Н, взяв операцию ротора от уравнения (2.16),

(2.39)

Рассмотрим решение уравнения (2.38) в разных средах.

В частном случае, когда среда однородна по координатам пространства ε=const и не зависит от частоты, уравнение (2.38) принимает вид:

(2.40)

Такой же вид в данной среде принимает и уравнение (2.39). Уравнение (2.40) справедливо для любой компоненты поля в декартовой системе координат. В цилиндрической системе координат оно справедливо только для составляющей Ez. Величина имеет физический смысл скорости в среде с диэлектрической и магнитной проницаемостями ε/ε0 и μ/μ0, где ε0, μ0 — диэлектрическая и магнитная проницаемости вакуума. Как отмечалось ранее, в оптических средах везде считается, что μ/μ0=1.

Решение уравнения (2.40) может удовлетворяться любой функцией [8]:

, (2.41)

если существует вторая производная от ψ. Это решение представляет плоскую волну. В выражении (2.41) компоненты r являются координатами точки наблюдения, n — единичный вектор, номальный к плоскости, а v не зависит от частоты. Действительно, при фиксированном значении времени t и заданном значении аргумента этой функции

(2.42)

функция ψ (u) имеет соответствующее фиксированное значение. Поэтому ψ (u) имеет одно и то же значение на этой бесконечной плоскости. Каждому приращению Δt соответствует приращение Δr, так что величина (2.42) остается неизменной, т.е.

. (2.43)

Вектор n является нормалью как к первоначальной, так и к смещенной плоскости. Из (2.42) следует, что плоскость движется в пространстве со скоростью v. Частным случаем являются такие решения уравнения (2.40), которые в каждой точке пространства изменяются во времени по косинусоиде

. (2.44)

Вектор называется волновым вектором. Все частотные составляющие сигнала распространяются с одной и той же фазовой скоростью. Следовательно, сигнал не претерпевает дисперсии.

В однородной дисперсионной среде при ε=ε(ω) и v=v(ω) решение (2.41) является приближенным, если дисперсия слабо выражена. В компонентах ВОСП это условие обычно выполняется.

Рассмотрим два случая: возбуждение сигнала ψ(t) некоторой светящейся плоскостью и некоторой светящейся поверхностью неплоской структуры.

Пример первый. Если некоторый сигнал ψ(t) возбуждается некоторой светящейся плоскостью, на которой этот сигнал можно представить в виде суперпозиции синусоидальных колебаний с помощью преобразования Фурье, то каждое гармоническое колебание (2.44) распространяется через дисперсионную среду как плоская волна. Такого типа волну ψ(t) можно представить в виде комплексного интеграла Фурье, располагая систему координат для удобства таким образом, чтобы она распространялась вдоль оси z. Тогда

(2.45)

Амплитудная функция φ(ω) определяется через известную форму сигнала при z=0:

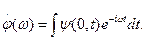(2.46)

Таким образом, сигнал в пространстве дисперсионной среды представляется совокупностью волн, каждая из которых находится в своей плоскости и движется со своей скоростью.

Пространственная длительность сигнала (Δz), представленная на рис. 2.18, определяется расстоянием между плоскостью 1 с гармоническим колебанием сигнала частотой и плоскостью N с гармоническим колебанием ω2.

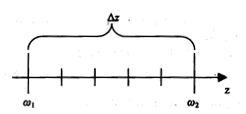
Рис. 2.18. Пространственная длительность сигнала, ?z в однородной дисперсионной среде

Напомним, что эти представления пригодны для случая, когда v слабо зависит от частоты или функция ψ(z,t) описывается узким спектром частот по сравнению с оптической несущей. Последнее условие в ВОСП также выполняется.

Фазовая скорость не имеет смысла для функции (2.45), однако эта функция правильно описывает распространение плоской волны общего вида в дисперсионной среде.

Изложенные выше представления полей, распространяющихся в дисперсионной среде, можно использовать и в случае возбуждения сигнала ψ(t) некоторой светящейся поверхностью неплоской структуры.

Пример второй. Криволинейную поверхность представим в виде совокупности плоских волн. На выходе реальных источников излучения, которыми являются лазеры, колебания сферические. Поэтому на малом расстоянии от лазера излучение представляется совокупностью плоских волн.

Используя суперпозицию плоских синусоидальных волн со всевозможными частотами, бегущих во всевозможных направлениях, можно составить общее выражение для волны, распространяющейся в дисперсионной среде:

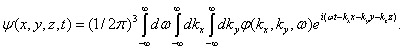(247)

Здесь kz или любая другая составляющая волнового вектора должна удовлетворять условию:

. (2.48)

Составляющая kz, может быть мнимой, когда подкоренное выражение отрицательно. В этом случае вместо плоской волны имеем дело с нераспространяющейся (локальной) волной. Такие волны также являются решениями волнового уравнения (2.40).

Интегральное представление (2.47) более общей волны состоит из плоских волн всевозможных направлений распространения и всевозможных частот, а также и из нераспространяющихся (локальных) волн. При гармоническом (синусоидальном) сигнале интегрирование по частоте можно исключить.

2.4.4. Граничные условия

Уравнения Максвелла в дифференциальной форме (2.16), (2.17) справедливы для линейных сред, параметр ε которых либо не зависит от координат, либо является непрерывной функцией координат. На практике, часто рассматриваемая область состоит из двух (или более) разнородных сред. При анализе макроскопических свойств поля в этих случаях обычно приходится считать, что параметр ε на границе раздела сред меняется скачком. Операция дифференцирования в точках, принадлежащих границе раздела, незаконна, и уравнения Максвелла в дифференциальной форме в этих точках теряют смысл. Поэтому для изучения поведения векторов электромагнитного поля при переходе из одной среды в другую нужно исходить из уравнений Максвелла в интегральной форме, которые остаются справедливыми и в этих случаях. Соотношения, показывающие связь между значениями векторов электромагнитного поля в разных средах у поверхности раздела, называются граничными условиями. Уравнения Максвелла не определяют электромагнитное поле полностью без задания граничных условий.

В задачах о неоднородных структурах без скачкообразного изменения граничным условием обычно является требование исчезновения поля в бесконечности и ограниченность поля внутри любой конечной области пространства. Требование отсутствия поля в бесконечности приводит к направляемым модам (типам волн), поле которых ограничено направляющей структурой (системой), при этом не теряется их мощность на излучение.

Наиболее общий тип граничных условий в световодных устройствах соответствует кусочно-однородному распределению ε. Представляют интерес граничные условия для переменных во времени полей. Искомые граничные условия получаются из уравнений Максвелла путем интегрирования их по объему, выбираемому на границе раздела сред. Стягивая объем в точку, в пределе получаем равенство тангенциальных составляющих электрического и магнитного полей на границе раздела сред:

Н_t1=H_t2, E_t1=E_t2 (2.49)

Физический смысл этих соотношений состоит в том, что тангенцианальные составляющие полей Н и Е непрерывны на границе раздела сред. Граничные условия совместно с условиями на бесконечности определяют конкретные решения уравнений Максвелла для конкретной задачи. При этом поля представляются в виде некоторых функций координат, частот и времени. В этом состоит волновой метод решения задач.

2.4.5. Волновой анализ распространения мод

Проведем волновой анализ распространения мод на примере ОВ со ступенчатым ППП. Для этого рассмотрим ОВ без потерь двухслойной конструкции (рис. 2.19).

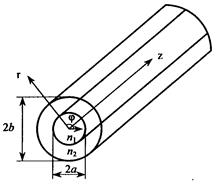
Рис. 2.19. Конструкция ОВ двухслойной структуры

Лучевой метод расчета волоконных световодов не дает полной картины распространения волн в ступенчатом ОВ. Поэтому необходимо обращаться и к волновому методу решения уравнений Максвелла или волнового уравнения.

Волновое уравнение (2.40) в цилиндрической системе координат r, φ, z относительно компонентов электрического поля или магнитного поля Н_z изменяющихся во времени t и вдоль оси z волокна, в виде

(2.50)

переходит в уравнение Гельмгольца:

(2.51)

где 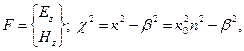(2.52)

χ - поперечное волновое число, или собственное значение; β— фазовая постоянная.

Для описания поведения электромагнитного поля в сердцевине (0<r<a) и в оболочке (а<r<b) необходимо использовать различные функции. Исходя из физической сущности процессов, функции сердцевины при r = 0 должны быть конечными, а в оболочке должны описывать спадающее поле. Используем цилиндрическую систему координат, ось которой совместима с осью цилиндра. Поверхностные составляющие напряженности электрического и магнитного полей могут быть выражены через продольные составляющие Е_z и Н_z. Для простоты решения уравнения (2.51) предположим, что оболочка ОВ с n₂ на рис. 2.19 простирается до бесконечности (d=∞). Такое упрощение модели является оправданным и приводит к адекватным характеристикам мод реального ступенчатого ОВ, имеющего защитное покрытие, обеспечивающее механическую защиту ОВ. В таком случае n в формуле (2.52) равно или n₁ в середине ОВ, или п₂ во внешней среде. Для нахождения бегущих вдоль оси z волн необходимо для внешней среды положить

(2.53)

чтобы поле в радиальном направлении в среде п₂ убывало. Тогда решение уравнения (2.51) можно записать:

для сердцевины ОВ с показателем преломления n₁ в виде:

(2.54)

(2.55)

Зависимость всех полей от координат φ в виде cosnφ и sinnφ свидетельствует о том, что в волокнах круглого сечения моды на равных могут существовать в виде двух взаимно ортогональных поляризаций. Это значит, что моды в ступенчатом ОВ являются попарно вырожденными по поляризации, что особенно важно для передачи сигналов в одномодовом ОВ. Таким образом, решения (2.54) и (2.55) дают возможность изучить условия распространения волн в ступенчатом ОВ. В решениях (2.54) и (2.55) А_m, В_m, С_m и D_m — постоянные интегрирования; J_n, N_n — функции Бесселя первого и второго рода n-го порядка, соответственно; I_n и K_n –видоизмененные (модифицированные) функции Бесселя первого и второго рода п-го порядка, соответственно. Качественные характеристики функции в зависимости от собственных значений χ₁r и a₂r приведены на рис. 2.20.

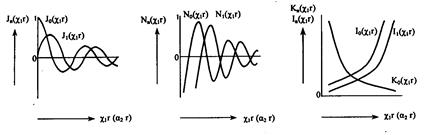
Рис. 2.20. Качественные зависимости функций J_n (χ₁r),

N_n(χ₁r), I_n(χ₁r) и K_n(χ₁r) от аргумента χ₁r(а₂r)

При r→0 значение N_n →-∞. Но так как поле на оси сердцевины не может приобретать бесконечные значения, то необходимо положить В_m =0. Поле за пределами сердцевины должно убывать в радиальном направлении и при r→∞ должно стремиться к нулю. Однако I_n при этом стремится к бесконечности, что противоречит условию Зоммерфельда. Следовательно, надо положить C_m = 0, так как нас интересуют только направляемые моды вдоль оси z. Таким образом, функция J_n(χ₁r) описывает распределение поля внутри сердцевины ОВ, а функция K_n(а₂r) описывает изменение поля за ее пределами (в среде с п₂) и ведет себя при больших значениях а₂r как exp( - а₂r). Тогда уравнения (2.54) и (2.55) перепишутся в виде:

(2.56)

(2.57)

Постоянные интегрирования А_т и D_т могут быть определены на основании граничных условий, как отмечалось ранее. Поперечные составляющие электрических (Е_r, Е_φ) и магнитных (Н_r, Н_φ)полей могут быть выражены с помощью известных соотношений между поперечными и продольными (Е_z, Н_z) составляющими. Тогда, используя условие равенства тангенцианальных составляющих напряженностей электрических и магнитных полей на поверхности раздела сердцевина — оболочка (при r =a):

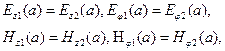(2.58)

найдем постоянные интегрирования. Подставим их в уравнения типа (2.56) и (2.57), и после соответствующих преобразований получим следующее характеристическое уравнение:

(2.59)

Это уравнение позволяет определить структуру поля, параметры волн и характеристики ОВ. В общем случае оно имеет ряд решений, каждому из которых соответствует определенная структура поля, называемая типом волны, или модой. Обычно в ступенчатых ОВ, применяемых для линий передачи сигналов, n₁≈n₂. Тогда уравнение (2.59) можно переписать в виде:

(2.60)

В ступенчатом ОВ отсечка моды (критические условия) наступает при равенстве поперечного волнового числа в оболочке -α₂=0, это возможно при β=k₂. При этом условии из (2.60) следует, что

(2.61)

Отсюда видно, что низшая (основная) мода (п=0) имеет отсечку, определяемую из уравнения:

Первый корень этого характеристического уравнения χ₁а= 0, и он соответствует моде НЕ₁₁. В соответствии с решением (2.54) и (2.55) эта волна существует в виде двух взаимных ортогональных поляризаций НЕ_11r и НЕ_11B соответствующих cosφ и sinφ (рис. 2.21). Распределение плотности поперечного поля в поперечном сечении сердцевины подчиняется закону J₀(χ₁r), приближающемуся к Гауссовому закону exp(–r²/ω₀²) распределения поля в лазерном световом пучке. Вторая в порядке возбуждения мода для n=0 отсекается, когда функция J₁(χ₁r) второй раз становится равной нулю, т.е. когда χ₁а= 3,83 (рис. 2.22). Эта мода обозначается НЕ₁₂. Аналогично для n=0 следуют моды НЕ₁₃, НЕ₁₄…

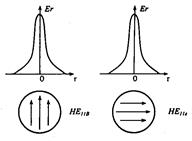
Рис. 2.21. Пример двух взаимноортогональных поляризаций моды НЕ11

В приведенных обозначениях мод первый индекс учитывает порядок функции, второй—номер корня (порядок решения), удовлетворяющего граничным условиям для данного порядка функции Бесселя.

Следующая совокупность мод соответствует n=1 или характеристическому уравнению:

. (2.62)

Первым корнем этого уравнения является χ₁а=2,405. Ему соответствуют две волны Н₀₁ и E₀₁. Второму корню уравнения (2.62) соответствует следующая пара мод Н₀₂ и Е₀₂ и т.д.

В качестве примера значения части корней бесселевых функций P_пт = χ₁а в зависимости от порядка функций и корня бесселевой функции, приведены в табл. 2.3.

Таблица 2.3. Значения корней бесселевых функций P_пт

Таким образом, функции Бесселя первого рода п-гo порядка дают бесконечное число корней. Причем корни функции J₀(χ₁а) определяют структуру поля симметричных волн (E_om,H_om), а J_п(χ₁а) при п≠0 структуру несимметричных гибридных волн (EН_om,HЕ_om). В индексе моды п — число изменений поля по диаметру, а т — число изменений поля по периметру сердцевины ОВ.

Симметричные волны электрические E_om и магнитные H_om имеют круговую симметрию (n=0). Раздельное распространение по световоду несимметричных волн типа Е_пт и Н_пт невозмоно. В ОВ они существуют только совместно, т.е. имеются продольные составляющие Е и Н. Эти волны называются гибридными, дипольными и обозначаются через НЕ_пт, если поле в поперечном сечении напоминает поле Н, или E_пт, если поле в поперечном сечении ближе к волнам Е.

2.4.6. Глоговское группирование мод

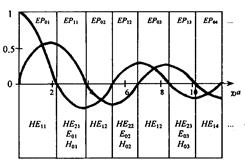
Рис. 2.22. Группирование мод по областям значений между соседними корнями функции J0(χ1а) и J1(χ1а)

Когерентные источники оптического излучения чаще всего создают линейно-поляризованный свет, и поэтому первично в волокне возбуждаются волны, не похожие на НЕ и ЕН волны. Это даже поставило под сомнение правильность индексации указанных волн. Впервые эту трудность разрешил Глог, сгруппировав моды по областям значений χ₁а между соседними корнями функций J₀(χ₁а) и J₁(χ₁а), как указано на рис. 2.22 и приведено в табл. 2.4.

Суммы полей указанных групп волн дают соответствующие линейно-поляризованные моды, обозначаемые LP_пт, или моды поляризации, обозначаемые ЕР_пт.

На рис. 2.23 а, б представлены, например, суммы полей волн Н₀₁ с собственным значением χ₁а=2,405 и НЕ₂₁ с собственным значением χ₂₁а =3,05, образующих поля двух волн LР₁₁ единой линейной в поперечном сечении ОВ поляризации, указанных стрелками. Аналогично суммы полей волн Е₀₁ и НЕ₂₁ (рис. 2.23 в, г) дают еще две линейные поляризации волны LP_пт. Волны LP_пт с единой линейной поляризацией представляют собой лишь приближение действительных собственных НЕ_пт и ЕН_пт волн сердечника. Вообще, любая LP_1т, волна состоит из Н_0т и НЕ_2т, волн при одной поляризации и из E_0т и НЕ_2т волн при другой поляризации. Волна LP_пт более высокого порядка и по окружности состоит из волн ЕН_п-1,т и НЕ_п+1,т. Более точно, конечно, использовать спектр волн ЕН_пт и НЕ_пт. Но для слабонаправляюших ОВ с n₁≈n₂ удобнее использовать LP волны. Только тогда, когда LP волны проходят по ОВ большое расстояние, они расщепляются на собственные НЕ и ЕН волны вследствие различия их собственных значений (фазовых скоростей).

Таблица 2.4. Группирование мод по Глогу

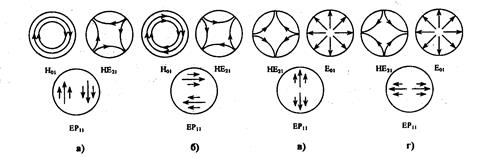
Рис. 2.23. Суммы полей волн Н₀₁ и НЕ₂₁ (Е₂₁ и НЕ₂₁)

Таким образом, при вводе из лазера линейно-поляризованного излучения в ступенчатое оптическое волокно, поддерживающее собственные моды НЕ_пт и ЕН_пт наблюдается их несогласованность как по структуре полей, так и по поляризации. Это приводит к сильному преобразованию волн на начальном участке ОВ и, как следствие, к большим потерям сигналов за счет излучения части их мощности в открытое пространство в виде вытекающих мод. Длина установления равновесного состояния мод может быть определена по приближенной формуле:

(2.63)

и может достигать значений от единиц сантиметров до сотен метров. Например, в случае типичного многомодового ОВ с радиусом сердцевины а=25 мкм, θ_кр=0,14 и v=30, L_y =300 м.

Картина высвечивания вытекающих мод на участке установления равновесного состояния мод представлена на рис. 2.24. Под L_у понимается длина ОВ, на которой излучается 0,9 мощности всех вытекающих мод.

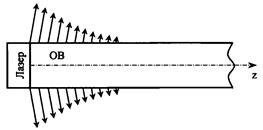
Рис. 2.24. Высвечивание вытекающих мод из МОВ на участке L_y

2.5. Параметры оптических волокон

2.5.1. Геометрические и оптические параметры оптических волокон

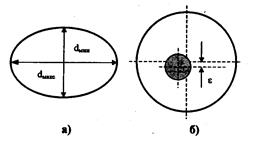
Рис. 2.25. Примеры неоднородностей в ОВ: а – некруглость; б – неконцентричность сердцевины и оболочки ОВ

Основными геометрическими параметрами ОВ являются: диаметр сердцевины; диаметр оболочки; диаметр защитного покрытия; некруглость (эллиптичность) сердцевины; некруглость оболочки; неконцентричность сердцевины и оболочки.

Некруглость сердцевины ОВ определяется как разность максимального и минимального диаметров сердцевины, деленная на номинальный диаметр сердцевины, и определяется только в многомодовых волокнах, некруглость оболочки — в многомодовых и одномодовых волокнах. Некруглость сердцевины ОВ (рис 2.25 а) определяется из выражения:

(2.64) где Н_­с — некруглость сердцевины, %; d_макс, d_мин — наибольший и наименьший диаметр сердцевины, мкм, соответственно; d_н — номинальный диаметр сердцевины, мкм.

Некруглость оболочки ОВ определяется аналогично.

Неконцентричность сердцевины относительно оболочки определяется как расстояние между центрами оболочки и сердцевины ОВ (рис. 2.25 б) и определяется из выражения:

(2.65)

где Н_с/о — неконцентричность сердцевины относительно оболочки, мкм; Ц_с — координаты центра сердцевины, мкм; Ц_о — координата центра оболочки, мкм.

Геометрические параметры стандартизированы для разных типов ОВ [9, 10, 11, 12, 13].

Поэтому остановимся более подробно на оптических параметрах ОВ.

Основными оптическими параметрами волокна являются:

• относительная разность показателей преломления (Δ);

• числовая апертура(NА);

• нормированная частота (v);

• число распространяющихся мод (М);

• диаметр модового поля (d_мп);

• длина волны отсечки (критическая длина волны λ_кр).

Относительная разность показателей преломления. Относительная разность ПП сердцевины и оболочки ОВ определяется выражением (2.12).

Числовая апертура. Одной из основных характеристик, определяющих условия ввода оптических сигналов и процессы их распространения в ОВ, является числовая апертура, определяемая для:

• оптических волокон со ступенчатым ППП

(2.66)

• оптического волокна с градиентным профилем ППП

(2.67)

В градиентных ОВ используется понятие локальной числовой апертуры. Ее значение

максимально на оси волокна и равно 0 на границе раздела сердцевина — оболочка.

Нормированная частота. Этот параметр, определяющий число мод, равен:

(2.68)

где λ — длина волны, мкм.

Если 0<v<2,405, то режим работы волокна одномодовый, если v>2,405 — многомодовый. Чем меньше диаметр сердцевины ОВ, тем меньшее число мод может распространяться по нему и тем меньшее расширение получают оптические импульсы. Соответственно увеличивается коэффициент широкополосности ОВ. Таким образом, одномодовое (ООВ) может передавать более широкополосные сигналы, чем многомодовое (МОВ).

Число мод в многомодовом оптическом волокне. Общее число мод в МОВ с диаметром сердцевины 2а, заданной числовой апертурой на рабочей длине волны λ определяется через нормированную частоту выражением вида:

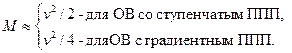(2.69)

В расчетах М может оказаться дробным числом, в то время как число мод в волокне бывает только целым и составляет от одной до тысячи мод. В волокне с градиентным ППП и теми же значениями диаметра сердцевины, показателей преломления п₁ и п₂ число мод примерно в 2 раза меньше, чем в ОВ со ступенчатым ППП. Количество мод (с учетом всех вырожденных мод) в случае ступенчатого ППП (2.2) определяется выражением вида:

(2.70)

где u — показатель степени, описывающий изменения ППП.

Диаметр модового поля в ООВ. Важным интегральным параметром ООВ является диаметр модового поля. Этот параметр используется при анализе одномодовых волокон.

В многомодовых ОВ размер сердцевины принято оценивать диаметром (2а), в одномодовых волокнах — с помощью диаметра модового поля (d_МП). Это связано с тем, что энергия основной моды в ООВ распространяется не только в сердцевине, но и частично в оболочке, захватывая ее приграничную область. Поэтому d_МП более точно оценивает размеры поперечного распределения энергии основной моды. Величина d_МП является важной при стыковке волокон между собой, а также при стыковке источника излучения с волокном.

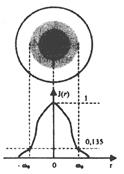
Рис. 2.26. Зависимость распределения интенсивности излучения основной моды ООВ в ближней зоне от радиуса

В [14] показана зависимость распределения интенсивности (мощности) излучения основной моды одномодового волокна в ближней зоне от радиуса (рис.2.26). Эта зависимость аппроксимируется с достаточной степенью точности формулой Гаусса:

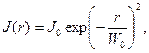(2.71)

где J(r) — интенсивность излучения на расстоянии r от оси ООВ; J₀ — интенсивность излучения на оси ООВ (при r=O); W_o — радиус модового поля, т. е. значение радиуса, при котором интенсивность излучения составляет 1/е² = 0,35J₀ .

Согласно [6, 15] радиус поля моды W_o в микрометрах определяется при известных значениях v и а=d_c/2 из соотношения

или

(2.72)

Тогда искомое значение диаметра модового поля равно d_МП=2W₀.

Длина волны отсечки в ООВ. Минимальная длина волны, при которой ОВ поддерживает только одну распространяющуюся моду, называется длиной волны отсечки. Этот параметр характерен для ООВ. Если λ_кр меньше, чем длина волны отсечки, то имеет место многомодовый режим распространения света.

Согласно [10] различают длину волны отсечки в волокне λ_с и длину волны отсечки в волокне λ_с и длину волны отсечки в проложенном кабеле λ_сс. Первая (λ_с) соответствует слабо напряженному волокну и для ступенчатого ООВ она определяется выражением вида:

(2.73)

Длина отсечки в проложенном кабеле λ_сс соответствует напряженному ОВ. На практике ОВ в проложенном или подвешенном на опорах кабеле имеет большое число изгибов. Кроме того, сильные искривления имеются в ОВ, уложенных в кассеты муфт и промежуточных соединителях на объектах связи (сплайс-боксах). Все это ведет к подавлению побочных мод и сдвигу λ_сс в сторону коротких длин волн в сравнении с λ_с. Разницу между λ_сс и λ_с можно оценить только экспериментальным путем.

2.5.2. Параметры передачи оптических волокон

К параметрам передачи ОВ относятся:

• коэффициент затухания;
• дисперсия ООВ;
• ширина полосы пропускания МОВ.

Коэффициент затухании оптического сигнала. Затухание в оптическом волокне — это мера ослабления оптической мощности, распространяемой вдоль ОВ между двумя его поперечными сечениями на данной длине волны. Затухание в ОВ выражается в дБ. Коэффициент затухания в ОВ — это величина затухания на единице длины волокна и выражается в дБ/км. Коэффициент затухания в ОВ обуславливается собственными потерями волокна и выражается в виде:

, (2.74)

где α_рр, α_пт, α_ик, α_пр — составляющие коэффициента затухания за счет рэлеевского рассеяния, поглощения в материале волокна, инфракрасного поглощения и поглощения на примесях ОВ, соответственно.

В общем виде потери энергии в материале волокна зависят от поглощения световой энергии, наличия посторонних примесей, таких как гидроксильные группы (ОН), ионы металлов (железа, кобальта, никеля, меди) и других включений, а так же от потерь на поглощение передаваемой мощности в инфракрасной области сектора.

Общие потери на поглощение в ОВ определяются формулой:

(2.75)

Механизм основных потерь, возникающих при распространении по ОВ электромагнитной энергии, иллюстрируется рис. 2.27. Часть мощности, поступающей на вход световода Р_вх, рассеивается из-за изменения направления распространяемых лучей на нерегулярностях и их высвечивании в окружающее пространство (α_рр), другая часть мощности поглощается материалом ОВ (α_пм) в виде поляризации диполей ОВ, посторонними примесями, что проявляется в виде Джоулева тепла (α_пр). В результате мощность на выходе P_вых. уменьшается.

Потери на поглощение существенно зависят от чистоты материала и при наличии посторонних примесей могут быть значительными. Потери на рассеяние лимитируют предел минимально допустимых потерь в ОВ.

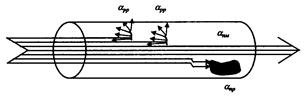
Рис. 2.27. Механизм основных потерь в световодах:

α_рр- рассеяние на нерегулярностях; α_пр- поглощение из-за примесей; α_пм- поглощение в материале волокна

Рассеяние, с одной стороны, обусловлено неоднородностями материала ОВ, размеры которых меньше длины волны, а с другой — тепловыми флуктуациями показателя преломления.

Рассеяние света принципиально неустранимо и вносит свой вклад в затухание ОВ даже в том случае, когда потери света на поглощение равны нулю.

Составляющую коэффициента затухания ОВ α_рр (дБ/км) за счет Рэлеевского рассеяния можно определить из выражения [4, 6]:

(2.76)

где n₁, — ПП сердцевины и равен 1,48 — 1,50; k=l,38·10^-23 Дж/К — постоянная Больцмана; Т=1500К — температура затвердевания стекла при вытяжке; β=8,1·10^-11 м²/Н — коэффициент сжимаемости (для кварца).

Составляющую α_пм (дБ/км), связанную с потерями на диэлектрическую поляризацию, можно определить из выражения:

(2.77)

где n₁ — показатель преломления сердцевины ОВ; tgδ — тангенс угла диэлектрических потерь сердцевины ОВ.

Составляющую α_ик(дБ/км), обусловленную электронным и атомным резонансами в инфракрасной части спектра за счет колебания атомов в кристаллической решетке, можно определить из выражения [6]:

(2.78)

где С и к — постоянные коэффициенты, равные, например, для кварца С=0,9, k=(0,7...0,9)10^-6 м.

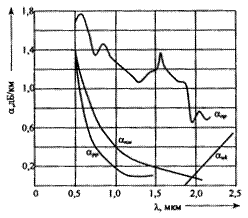
Рис. 2.28. Составляющие потерь энергии

На рис. 2.28 представлены типовые зависимости основных составляющих потерь от длины волны. Как видно из графика, рэлеевское рассеивание α_рр ограничивает нижний предел потерь в левой части, а инфракрасное поглощение α_ик — в правой части спектра волн.

В настоящее время в технике связи в основном применяются кварцевые ОВ, область эффективного использования которых находится в диапазоне длин волн до 2 мкм. При дальнейшем увеличении длины волны из-за значительных величин α_ик в ОВ кварц заменяется на другие материалы. В частности, в [16] сообщается об испытаниях фирмой Хьюз Эйркрафт волокон, выполненных из поликристалла бромистого и бромойодистого таллия и имеющих на длинах волн 4 — 5 мкм коэффициент затухания, равный 0,01 дБ/км.

На более длинных волнах в качестве материала для волокна используются галоидные, халькогенидные и фтористые стекла. По сравнению с кварцевыми волокнами они обладают большей прозрачностью и обеспечивают снижение потерь на несколько порядков. С появлением ОВ из новых материалов становится реальным создание ВОЛС без регенераторов. Известны проекты строительства подводной оптической линии через Атлантический океан протяженностью 6000 км без регенераторов, в которых анализируется возможность применения ОВ из тетрафторида, изиркония и фторида бериллия [17].

Так как теоретические расчеты потерь на рэлеевское рассеяние и поглощение представляют собой сложную задачу и точность таких расчетов мала, то при практических расчетах α удобно применять следующие приближенные формулы [18]:

(2.79)

где α_рр — составляющая коэффициента затухания ОВ за счет рэлеевских потерь, дБ/км; λ — длина волны оптического излучения, введенного в ОВ, нм;

при расчете α_рр в одномодовых ОВ второе слагаемое отбрасывается [8]:

, (2.80)

где α_рр — составляющая а за счет материальных потерь ОВ, дБ/км;

, (2.81)

где α_ик — составляющая α ОВ за счет потерь в инфракрасной области, дБ/км.

Из потерь на примесях в реальных ОВ, выпускаемых в соответствии с требованиями ITU — TG.651, G.652 [9, 10], наиболее сильно проявляются потери на гидроксильном остатке воды (ОН), значения которых согласно [13] следующие:

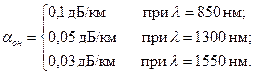(2.82)

При правильном выборе материала для ОВ и рабочей длины волны λ суммарное оценочное значение коэффициента затухания ОВ, выраженное рэлеевскими потерями и общими потерями за счет поглощения, может быть определено согласно [6] выражением:

(2.83)

где α — коэффициент затухания ОВ, дБ/км; k_п = 0,1 —0,25 — экспериментальный поправочный коэффициент, учитывающий потери на поглощение.

Дисперсия оптического сигнала. Наряду с коэффициентом затухания ОВ важнейшим параметром является дисперсия, которая определяет его пропускную способность для передачи информации.

Дисперсия — это рассеивание во времени спектральных или модовых составляющих оптического сигнала, которое приводит к увеличению длительности импульса оптического излучения при распространении его по ОВ (рис. 2.29) и определяется разностью квадратов длительностей импульсов на выходе и входе ОВ [3]:

(2.84)

где значения τ_вых и τ_вх определяются на уровне половины амплитуды импульсов.

Дисперсия не только ограничивает частотный диапазон ОВ, но существенно снижает дальность передачи сигналов, так как чем длиннее линия, тем больше увеличение длительности импульсов. Дисперсия в общем случае определяется тремя основными факторами: различием скоростей распространения направляемых мод, направляющими свойствами оптического волокна и параметрами материала, из которого оно изготовлено. В связи с этим основными причинами возникновения дисперсии являются, с одной стороны, большое число мод в ОВ (межмодовая дисперсия), а с другой стороны — некогерентность источников излучения, реально работающих в спектре длин волн Δλ (хроматическая дисперсия).

Межмодовая (модовая) дисперсия преобладает в многомодовых ОВ. Она обусловлена наличием большого количества мод, время распространения которых различно. Для ОВ со ступенчатым профилем показателя преломления скорость распространения электромагнитных волн с длиной волны λ одинакова и равна:

(2.85)

где с — скорость света, км/с.

В этом случае все лучи, падающие на торец ОВ под углами к его оси в пределах апертурного угла θ_а движутся в сердцевине волокна по своим зигзагообразным линиям и при одинаковой скорости распространения достигают приемного конца в разное время, что естественно, приводит к увеличению длительности принимаемого импульса (рис. 2.29). Все лучи, падающие на торец ОВ под углами к его оси в пределах 0< θ_п < θ_а достигают приемного устройства с некоторым временным сдвигом, что, естественно, приводит к увеличению длительности принимаемого импульса.

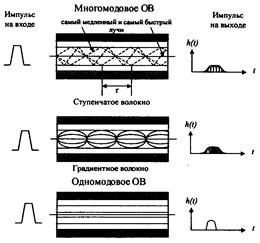
Рис. 2.29. Распространение излучения по ступенчатому и градиентному многомодовым и одномодовому ОВ

Межмодовая дисперсия градиентных ОВ, как правило, на порядок и более ниже, чем у ступенчатых волокон. Это обусловлено тем, что за счет уменьшения показателя преломления от оси ОВ к оболочке скорость распространения лучей вдоль их траекторий изменяется — так, на траекториях, близких к оси, она меньше, а на удаленных, естественно, — больше. Следовательно, лучи, распространяющиеся кратчайшими траекториями (ближе к оси), обладают меньшей скоростью, а лучи, распространяющиеся по более протяженным траекториям, имеют большую скорость. В результате время распространения лучей выравнивается и увеличение длительности импульса становится меньше.

Расширение импульса из-за модовой дисперсии характеризуется временем нарастания сигнала и определяется как разность между самым большим и самым малым временем прихода лучей в сечение световода на расстоянии l от начала.

Согласно законам геометрической оптики время распространения луча в ступенчатом многомодовом ОВ зависит от угла падения О„и, как было показано в [17], определяется выражением:

(2.86)

где L — длина световода, км; n_­1 — показатель преломления сердцевины ОВ; с — скорость света, км/с.

Так как минимальное время распространения оптического луча имеет место при θ_п =0, а максимальное при θ_п = θ_кр, соответствующие им значения времени распространения можно записать: (2.87)

откуда значение межмодовой дисперсии равно:

(2.88)

где τ_мм — межмодовая дисперсия, пс.

Из последнего выражения следует, что межмодовая дисперсия возрастает с увеличением длины волокна. Однако это справедливо только для идеального волокна, в котором взаимодействие между модами отсутствует. В реальных условиях наличие неоднородностей, кручение и изгиб волокна приводят к постоянным переходам энергии из одних мод в другие, т.е. к взаимодействию мод, в связи с чем дисперсия становится пропорциональной . Эго влияние проявляется не сразу, а после определенного расстояния прохождения световой волны, которое носит название длины установившейся связи мод и принимается равным 5 — 7 км для ступенчатого волокна и 10 — 15 км — для градиентного. Оно установлено эмпирическим путем.

В градиентных многомодовых волокнах время распространения оптических лучей определяется законом изменения показателя преломления и при определенных условиях выравнивается, что, естественно, уменьшает дисперсию. Так, при параболическом профиле показателя преломления, когда показатель степени в выражении (2.2) принимает значение и=2,

(2.89)

Наименьший разброс групповых задержек из всех ППП, описываемых (2.2), получается при показателе степени и=и_опт, т.е. при и_опт=2(1 – ) [8]. При этом τ_мод достигает минимального значения (рис. 2.30), равного

(2.90)

Из этого рисунка τ_мод может быть представлено в виде:

(2.91)

Характер кривой на рисунке свидетельствует, что для минимизации дисперсии необходимо тщательно управлять значением и, что на практике оказывается нелегким делом. А всякое изменение профиля, приближающееся к параболическому, существенно уменьшает модовую дисперсию в таком градиентном ОВ.

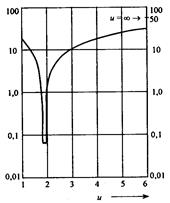
Рис. 2.30. Зависимость модовой дисперсии ΔτСП от степени и в градиентных ОВ

При анализе выражений (2.88) и (2.89) становится очевидным, что межмодовая дисперсия градиентного ОВ в раз меньше, чем у ступенчатого при одинаковых значениях . А так как обычно 1 %, то межмодовые дисперсии указанных ОВ могут отличаться на два порядка.

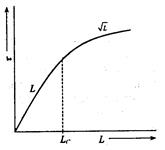
Рис. 2.31. Длина взаимодействия мод

В инженерных расчетах при определении модовой дисперсии следует иметь ввиду, что до определенной длины линии L_с нет межмодовой связи, а затем при L>L_с происходит процесс взаимного преобразования мод и наступает установившийся режим. Поэтому, как видно из рис. 2.31, вначале, при L< L_с, дисперсия увеличивается по линейному закону, а затем, при L>L_с по квадратичному закону. Следовательно, вышеприведенные формулы расчета модовой дисперсии справедливы лишь для длины линии L>L_с.

При длинах линии L>L_с следует пользоваться следующими формулами:

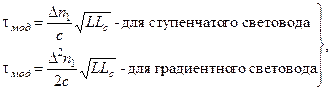(2.92)

где L — длина линии, км; L_c — длина связи мод (установившегося режима), км.

Дисперсионные свойства различных типов ОВ, выпускаемых по рекомендациям ITU-TG.651 и G.652, приведены в табл. 2.5. В ступенчатых световодах при многомодовой передаче доминирует модовая дисперсия и она достигает больших значений (20 — 50 нс/км).

Таблица 2.5. Дисперсионные свойства различных ОВ

Дисперсия	Причина дисперсии	Многомодовое ОВ		Одномодовое ОВ ( F=1-10 ГГц)
		Ступенчатое ( F=10-100 МГц)	Градиентное ( F=100-1000 МГц)
Волноводная	Коэффициент распространения зависит от частоты	Малое значение дисперсии	Малое значение дисперсии	Взаимная компенсация
Материальная	Показатель преломления зависит от частоты	(2 – 5)снс/км	(0,1 – 0,3) нс/км
Межмодовая	Разные моды приходят к концу линии в разное время	(20 – 50) нс/км	(1 – 4) нс/км	Отсутствует

Модовая дисперсия может быть уменьшена следующими тремя способами:

1. использованием ОВ с меньшим диаметром сердцевины, поддерживающей меньшее количество мод. Например, сердцевина диаметром 100 микрон поддерживает меньшее число мод, чем сердцевина в 200 микрон;
2. использованием волокна со сглаженным ППП, чтобы световые лучи, прошедшие по более длинным траекториям, имели скорость, превышающую среднюю, и достигали противоположного конца волокна в тот же момент времени, что к лучи, движущиеся по коротким траекториям;
3. использованием одномодового волокна, позволяющего избежать модовой дисперсии.

В одномодовых ступенчатых световодах отсутствует модовая дисперсия и дисперсия в целом сказывается существенно меньше. Здесь проявляются волноводная и материальная дисперсии и при длине волны порядка 1,3 мкм происходит их взаимная компенсация ( ).

Волноводная (внутримодовая) дисперсия обусловлена процессами внутри моды. Она характеризуется направляющими свойствами сердцевины ОВ, а именно: зависимостью групповой скорости моды от длины волны оптического излучения, что приводит к различию скоростей распространения частотных составляющих излучаемого спектра. Поэтому внутримодовая дисперсия, в первую очередь, определяется профилем показателя преломления ОВ и пропорциональна ширине спектра излучения источника , т.е.

(2.93)

где — удельная внутримодовая дисперсия.

При отсутствии значений оценка характеризуется выражением:

(2.94)

где — ширина спектральной линии источника излучения, равная 1 — 3 нм для лазера и 20 — 40 нм для светоизлучающего диода; L — длина линии,км; с — скорость света, км/с.

Материальная дисперсия в ОВ обусловлена зависимостью показателя преломления от длины волны В реальном ОВ распространение волн дисперсионно, т.е. скорость распространения зависит от частоты (длины волны). Различные длины волн (цвета) также движутся с различными скоростями по волокну, даже в одной и той же моде. Ранее мы видели, что показатель преломления равен n=c/v.

Рис. 2.32. Скорости распространения длин волн

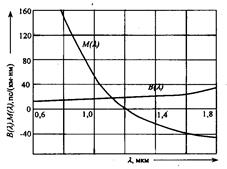
Рис. 2.33. Удельные значения дисперсии при различных длинах волн: В(λ)-волноводная; М(λ)-материальная

Поскольку каждая длина волны движется с разной скоростью, то величина скорости v в этом уравнении изменяется для каждой длины волны. Таким образом, показатель преломления изменяется в зависимости от длины волны. Дисперсия, связанная с этим явлением, называется материальной (молекулярной) дисперсией, поскольку зависит от физических свойств вещества волокна. Уровень дисперсии зависит от диапазона длин волн света, инжектируемого в волокно (как правило, источник излучает несколько, длин волн), а также от центральной рабочей длины волны источника. В области 850 нм более длинные волны (более красные) движутся быстрее по сравнению с более короткими (более голубыми) длинами волн. Волны длиной 860 нм движутся быстрее по стеклянному волокну, чем волны длиной 850 нм. В области 1550 нм ситуация меняется: более короткие волны движутся быстрее по сравнению с более длинными; волна 1560 нм движется медленнее, чем волна 1540 нм. В некоторой точке спектра происходит совпадение, при этом более голубые и более красные длины волн движутся с одной и той же скоростью. Это совпадение скоростей происходит в области 1300 нм, называемой длиной волны с нулевой дисперсией (рис. 2.33). Длина стрелок соответствует скорости длин волн; следовательно, более длинная стрелка соответствует более быстрому движению. Типичная картина удельной волноводной и материальной дисперсии вещества одномодового волокна приведена на рис. 2.33. На длине волны 1300 нм равна нулю. В области длин волн выше 1300 нм она отрицательна — волны отстают и прибывают позднее. В области менее 1300 нм волны опережают и прибывают раньше.

Как и волноводную дисперсию, модовую дисперсию можно определить через удельную дисперсию по выражению:

. (2.95)

Величина определяется экспериментальным путем. При разных составах легирующих примесей в ОВ имеет разные значения в зависимости от . Поэтому при инженерных расчетах для определения т можно использовать выражение:

(2.96)

Для определения можно воспользоваться формулой Селмейера для ПП кварцевогo стекла с использованием метода конечных разностей [19], откуда вычисляют величины , после чего находят

(2.97)

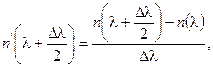(2.98)

а затем

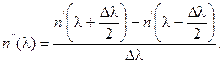(2.99)

Поляризационная модовая дисперсия возникает вследствие разной скорости распространения двух взаимоперпендикулярных поляризаций основной моды ОВ. Для оценки этого вида дисперсии используется выражение:

, (2.100)

где К_пмд — коэффициент удельной поляризационной дисперсии.

По определению поляризационная модовая дисперсия проявляется исключительно в одномодовых волокнах с нециркулярной (эллиптической) сердцевиной и при определенных условиях становится соизмеримой с хроматической дисперсией. Эти условия проявляются тогда, когда используется передача широкополосного сигнала (полоса пропускания 2,4 Гбит/с и выше) с очень узкой спектральной полосой излучения 0,1 нм и меньше.

Поляризационной дисперсии можно дать следующее пояснение. В ООВ распространяется не одна мода, а две фундаментальные моды — две взаимно перпендикулярные поляризации входного сигнала. В идеальном, т.е. однородном по геометрии, волокне две моды распространяются с одинаковой скоростью. Однако реальные ОВ имеют неидеальные геометрические размеры, что приводит к разным скоростям распространения этих двух мод с разными состояниями поляризации и, как следствие, к появлению поляризационной модовой дисперсии.

Поэтому результирующая дисперсия одномодового волокна должна определяться в соответствии с выражением:

(2.101)

В обычных условиях работы ООВ поляризационная модовая дисперсия достаточно мала и поэтому при расчетах полной дисперсии ею можно пренебречь.

В многомодовых ОВ волноводная дисперсия мала по величине, поэтому при определении полной дисперсии ею пренебрегают. В таких ОВ со ступенчатым ППП доминирует над , а с градиентным ППП определяющей становится материальная дисперсия. Последнее связано с тем, что в градиентных МОВ уменьшается за счет выравнивания времени распространения различных мод. Исходя из этого в общем виде полная дисперсия в МОВ может быть представлена выражением:

. (2.102)

В одномодовых ОВ модовая дисперсия отсутствует, так как по таким волокнам распространяется только одна мода НЕ₁₁ или, как отмечалось ранее, две моды в двух разных состояниях поляризации, но с одной дисперсионной зависимостью фазового коэффициента (в приближении линейно-поляризованных мод — LP₀₁ мода в двух взаимоортогональных поляризациях). Другими словами, расширение импульсов в ООВ определяется хроматической дисперсией в пределах этой моды. Тогда полная дисперсия в ООВ может быть представлена в общем виде выражением:

(2.103)

Сравнивая дисперсионные характеристики различных волокон, можно отметить, что наилучшими показателями обладают одномодовые ОВ, а наиболее сильно дисперсия проявляется в многомодовых ОВ со ступенчатым ППП.

Ширина полосы пропускания. Многие производители волокна и оптического кабеля не используют в спецификации дисперсию в многомодовых изделиях. Вместо этого они указывают произведение ширины полосы пропускания на длину, или просто полосу пропускания, выраженную в мегагерцах на километры. Полоса пропускания в 400 МГц км означает возможность передачи сигнала в полосе 400 МГц на расстояние 1 км. Это также означает, что произведение максимальной частоты сигнала на длину передачи может быть меньше или равно 400. Другими словами, можно передавать сигнал более низкой частоты на большее расстояние или более высокой частоты на меньшее расстояние, как показано на рис. 2.34.

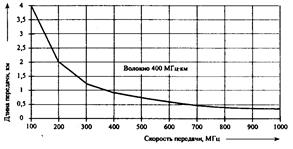
Рис. 2.34. Зависимость длины передачи от ширины полосы пропускания

Рабочая полоса частот (полоса пропускания) ОК определяет число передаваемых по нему каналов связи и лимитируется дисперсией ОВ.

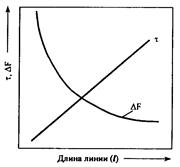
Рис. 2.35. Дисперсия τ и пропускная способность ΔF ОВ различной длины

На рис. 2.35 показан характер изменения дисперсии и пропускной способности ОВ в зависимости от длины линии. Снижение из-за дисперсии величины до допустимого значения лимитирует дальность передачи по ОК.

Полоса частот и дальность передачи l взаимосвязаны. Соотношение между ними выражается формулами (для коротких линий в пределах устанавливающегося модового режима) и (для длинных линий). В этих соотношениях параметры с индексом х — искомые, а без индекса — заданные; l_с — длина связи мод. В реальных условиях обычно формируется полоса пропускания на один километр и определяется полоса пропускания на всю линию по формулам:

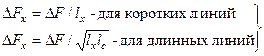(2.104)

Полоса пропускания зависит от расширения импульсов т и определяется соотношением .

2.5.3. Механические параметры оптических волокон

К механическим параметрам ОВ относятся:

• прочность волокна;
• динамическая прочность на разрыв;
• параметр нагрузки разрушения;
• стойкость к изгибам;
• усилие снятия защитного покрытия.

Прочность волокна. Стекло принято считать хрупким. Оконное стекло действительно не гнется. Однако стеклянные волокна можно согнуть в виде окружности небольшого диаметра или завязать в свободный узел, не повреждая их. (Затягивание тугого узла может повредить волокно.)

Предел прочности характеризует способность волокна противостоять натяжению или изгибу без повреждения. Предел прочности волокна на разрыв превосходит ту же величину для стальной нити идентичного размера. Более того, медный проводник должен иметь вдвое больший диаметр, чтобы обеспечить тот же предел точности, что и волокно.

Основная причина, обусловливающая хрупкость волокна, это наличие микротрещин на поверхности и дефектов внутри волокна. При этом поверхностные трещины более существенны. Поверхностные дефекты могут возрастать под воздействием растягивающей нагрузки, возникающей во время прокладки кабеля. Температурные изменения, механические и химические воздействия, обычное старение также приводят к появлению дефектов. Расширяющиеся дефекты приводят к случайному обрыву волокна. Для разрезания стекла делается узкая царапина на его поверхности. Затем, в результате резкого надлома, стекло трескается вдоль царапины. Аналогичный процесс происходит в волокне. Скрытые дефекты действуют аналогично царапине на поверхности стекла. Как только к волокну прикладывается достаточно сильное растягивающее напряжение, дефекты растут внутри волокна до тех пор, пока оно не разрывается.

Динамическая прочность на разрыв. Динамическая прочность ОВ на разрыв — это определенное значение интенсивности нагрузки на растяжение или сжимание, которой подвергается вся длина волокна в его осевом направлении на протяжении определенного кратковременного периода [20].

Величина динамической прочности на разрыв ОВ составляет обычно величину более чем 38 ГПа для образцов, не подвергшихся старению, длиной 0,5 м.

Параметр нагрузки разрушения. Параметр нагрузки разрушения — это безразмерный коэффициент, эмпирически связанный с зависимостью распространения разрушения (трещины) ОВ от приложенной нагрузки [20). Величина параметра нагрузки разрушения зовисит от окружающей температуры, влажности и других условий.

Статистические и динамические значения параметров нагрузки разрушения обычно задаются в технической документации на ОВ. Статические значения параметра нагрузки разрушения (п_с) — это отрицательная крутизна графика зависимости времени наработки ОВ на отказ через статическую усталость в зависимости от приложенной нагрузки в двойном логарифмическом масштабе.

Динамическое значение параметра нагрузки разрушения (п_д) — это такая величина, которая показывает, что значение 1/(п_д+1) есть крутизна графика динамической усталости в двойном логарифмическом масштабе в зависимости от скорости изменения напряжения в волокне, обусловленного приложенной нагрузкой. Значение параметра динамической усталости п_д определяется методом испытания динамической усталости.

Параметры п_с и п_д обычно указываются в технической документации на ОВ и, как пpaвило, их величина больше 20.

Стойкость к изгибам. Несмотря на то, что волокно может быть согнуто в окружность, оно имеет минимальный радиус изгиба. Достаточно резкий изгиб может разорвать волокна. Изгибы также приводят к двум другим эффектам.

1. Слегка увеличивается затухание. Этот эффект должен быть интуитивно понятен. Изгибы изменяют углы падения и отражения света внутри волокна настолько, что часть его, заключенная в модах высокого порядка, может покидать волокно (подобно случаю с микроизгибами).

2. Уменьшается предел прочности волокна на разрыв. Если растяжение сопровождается изгибом волокна, оно может разорваться при меньшем значении растягивающей нагрузки, чем в случае выпрямленного волокна.

Согласно спецификации на ОВ некоторых фирм минимальный радиус кривизны равен пяти диаметрам кабеля при отсутствии растягивающих напряжений и 10 диаметрам кабеля при их наличии.

Усилие снятия защитного покрытия. Этот параметр характеризует усилие, которое необходимо приложить для удаления покрытия с волокна, не подвергая последнее чрезмерному механическому напряжению, которое может привести к его разрыву. Как правило, усилие снятия защитного покрытия ОВ составляет величину, находящуюся в пределе от 1,3 Н до 9 Н.