При передаче информации по каналам связи в процессе преобразования сигналов в различных устройствах, как правило, используют негармонические колебания, поскольку чисто гармонические колебания не могут являться носителями информации. Для передачи сообщений осуществляют модуляцию гармонического колебания по амплитуде – амплитудная модуляция (AM), частоте – частотная модуляция (ЧМ) или фазе – фазовая модуляция (ФМ), либо используют импульсные сигналы, модулируемые по амплитуде – амплитудно-импульсная модуляция (АИМ), ширине – широтно-импульсная модуляция (ШИМ), временному положению – время-импульсная модуляция (ВИМ). Существуют и другие, более сложные сигналы, формируемые по специальным законам. Отличительной чертой указанных сигналов является сложный негармонический характер. Несинусоидальный вид имеют токи и напряжения, формируемые в различных импульсных и цифровых устройствах, несинусоидальный характер приобретают гармонические сигналы, проходящие через различные нелинейные устройства и т. д. Все это приводит к необходимости разработки специальных методов анализа и синтеза электрических цепей, находящихся под воздействием периодических несинусоидальных и непериодических токов и напряжений. В основе этих методов лежат спектральные представления несинусоидальных воздействий, базирующиеся на разложении в ряд или интеграл Фурье.

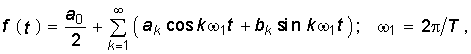Из математического анализа известно, что периодическая негармоническая функция f(t), удовлетворяющая условиям Дирихле, может быть разложена в ряд Фурье: (5.1) где a_k, b_k — коэффициенты разложения, определяемые уравнениями 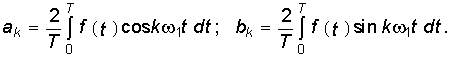(5.2)

Величина 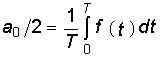представляет среднее за период значение функции f(t) и называется постоянной составляющей.

В теоретических исследованиях обычно вместо формулы (5.1) используют другую, основанную на замене независимой переменной : 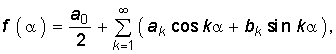(5.3) где 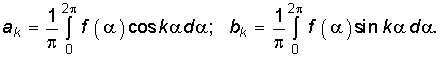(5.4)

Уравнение (5.3) есть тригонометрическая форма ряда Фурье. При анализе цепей часто удобней пользоваться комплексной формой ряда Фурье, которая может быть получена из (5.3) с помощью формул Эйлера: (5.5)

Подставив (5.5) в уравнение (5.3), после несложных преобразований получим комплексную форму ряда Фурье: 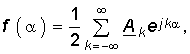(5.6) где A_k — комплексная амплитуда k-й гармоники: (5.7) где – амплитуда; – начальная фаза k-й гармоники.

Подставив значения a_k и b_k из (5.4) в (5.7), получим: 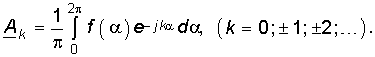(5.8)

Совокупность амплитуд 0,5А_k = 0,5А_–k в разложении (5.6), отложенных против соответствующих положительных и отрицательных частот, образует симметричный относительно оси координат (вследствие четности коэффициентов а_k) линейчатый амплитудный спектр.

Совокупность ординат _k = –_–k из (5.7), входящих в разложение (5.6) и отложенных против соответствующих положительных и отрицательных частот, образует симметричный относительно начала оси координат (вследствие нечетности коэффициентов b_k) линейчатый фазовый спектр.

Разложение (5.3) можно представить и в другой форме. Если учесть, что а_k = А_kcos _k и b_k = А_ksin _k, то после подстановки в (5.3) получим: 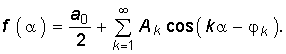(5.9)

Если рассматривать постоянную составляющую a₀/2 как нулевую гармонику с начальной фазой ₀ = 0, то разложение (5.9) примет вид 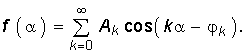(5.10)

В частном случае, когда функция f(a) симметрична относительно оси ординат (рис. 5.1, а), в разложении (5.3) окажутся только четные (косинусоидальные) гармоники: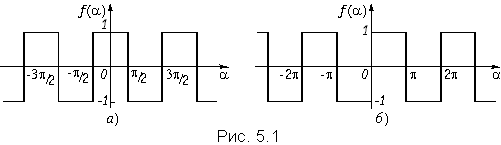

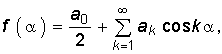(5.11)

а при симметричности f(a) относительно начала координат (рис. 5.1, б) нечетные гармоники 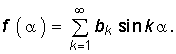(5.12)

При сдвиге начала отсчета функции f(a) ее амплитудный спектр не изменяется, а меняется только фазовый спектр. Действительно, сдвинем функцию f(a ) по оси времени влево на t₀ и обозначим .

Тогда разложение (5.9) примет вид 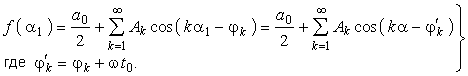(5.13)

Пример. Разложить в ряд Фурье прямоугольные колебания (рис. 5.1, б). Учитывая, что f(a) симметрична относительно начала координат в разложении (5.3) останутся только синусоидальные гармоники (5.12), где b_k определится согласно (5.4): 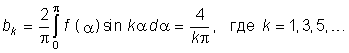Подставив b_k в (5.12), получим разложение в ряд Фурье: (5.14) Далее сдвинем f(a) на p/2 влево (см. рис. 5.1, а). Тогда согласно (5.13) получим 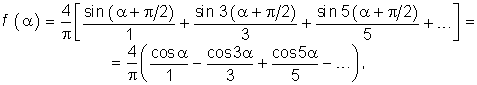(5.15) т. е. получили разложение по косинусоидальным составляющим как и должно быть для симметричного относительно оси ординат сигнала.

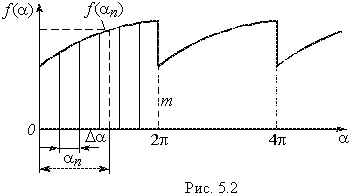
В ряде случаев, когда периодичная функция f(a) задана графически и имеет сложную форму, ее разложение в ряд Фурье можно осуществить графо-аналитическим способом. Его суть заключается в том, что период сигнала Т (рис. 5.2) разбивают на m интервалов, равных , причем точки разрыва f(a) не должны попадать на середину участков разбиения; определяют значение сигнала f(a_n) в середине каждого участка разбиения.

Находят коэффициенты разложения а_k и b_k путем замены интеграла в (5.2) конечной суммой 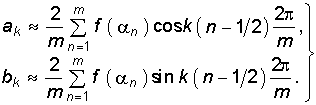(5.16)

Уравнение (5.16) легко программируется и при вычислении а_k и b_k, может использоваться ЭВМ.