Пусть S1(t) = A cos w1t, S2(t) = A cos w2t, 0 £ t £ T (дискретная частотная модуляция - ДЧМ).

Преобразуем выражение (4.4)

x2(t) - 2x(t)S1(t) + S21(t) < х2(t) - 2x(t)S2(t) + S22(t) , то S1.

Здесь S21(t) = S22(t), так как это мощности сигналов S1(t) и S2(t), а эти мощности равны между собой из-за равенства амплитуд этих сигналов. После очевидных сокращений получаем следующее оптимальное правило решения x(t)S1(t) > x(t)S2(t) , то S1 или, более кратко BxS1(0) > BxS2(0), то S1 . (6.1)

Смысл полученного выражения очевиден: если функция взаимной корреляции входного сигнала x(t) и сигнала S1(t) больше, чем функция взаимной корреляции сигналов x(t) и S2(t), то x(t) содержит, кроме помехи, сигнал S1(t).

Cигналы S1(t) и S2(t), используемые для вычисления функций взаимной корреляции, должны генерироваться в схеме приемника и совпадать по частоте и фазе с оптимальными сигналами, которые поступают или могут поступать на вход приемника.

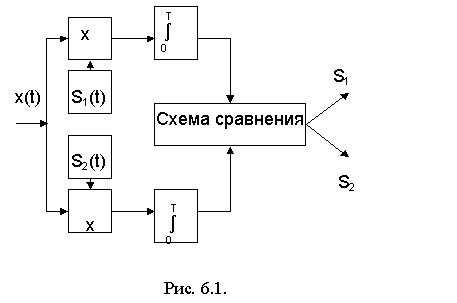
Схема, реализующая правило решения (6.1), также называется корреляционным приемником и приведена на рис. 6.1.

Схема содержит два коррелятора по числу передаваемых сигналов При приеме сигналов ДЧМ местные генераторы генерируют сигналы A cos w1t и A cos w2t. Эта же схема пригодна для приема дискретной фазовой мо-дуляции (ДФМ), если в качестве опорных сигналов использовать сигналы S1(t) = A cos w0t и S2(t) = - A cos w0t.

Если вероятности передачи сигналов S1(t) и S2(t) не одинаковы, т.е. P(S1) не равно P(S2), то неравенство (6.1) принимает несколько другой вид

x(t)S1(t) - s2n lnP(S1) > x(t)S2(t) - s2n lnP(S2) , то S1 , (6.2)

а в структурной схеме рис.6.1 перед схемой сравнения добавляются выравнивающие устройства, аналогично показанным на рис.4.2 .

Однако для приема сигналов ДФМ схему рис. 6.1. можно упростить, если использовать один общий коррелятор (рис. 6.2).

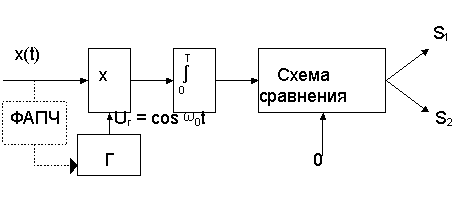
Если x(t) содержит сигнал S1(t) = A cos w0t, на выходе интегратора имеем напряжение, равное BxUг (0) > 0 . Если же x(t) содержит сигнал S2(t) = - A cos w0t, то на выходе интегратора имеем напряжение, равное BxUг (0) < 0. Напряжение на выходе интегратора сравнивается с пороговым напряжением, равным нулю, и в зависимости от результатов сравнения выдает сигналы S1 или S2.

В рассмотренных здесь корреляционных приемниках осуществляется когерентный прием сигналов, поэтому применяемые в приемниках генераторы должны выдавать опорные сигналы S1(t) и S2(t), совпадающие с аналогичными принимаемыми сигналами с точностью до фазы. Поэтому для работы рассмотренных здесь корреляционных приемников требуется синхронизация местных генераторов сигналов. На рис. 6.2, например, пунктиром показана цепь синхронизации опорного генератора Г входным сигналом x(t) с помощью специального устройства фазовой автоподстройки частоты (ФАПЧ).