3.1. Электрические процессы в коаксиальных цепях

3.2. Первичные параметры коаксиальной цепи

3.3. Вторичные параметры передачи коаксиальной цепи

3.1. Электрические процессы в коаксиальных цепях

Способность коаксиальной цепи (пары) пропускать широкий спектр частот конструктивно обеспечивается коаксиальным расположением внутреннего и внешнего проводников. Особенности распространения электромагнитной энергии по коаксиальной паре обусловливают возможность передачи широкого спектра частот и ставят высокочастотные связи в преимущественное положение по сравнению с низкочастотными. Как будет показано ниже, взаимодействие электромагнитных полей внутреннего и внешнего проводников коаксиальной пары таково, что внешнее поле равно нулю. Рассмотрим раздельно электрическое и магнитное поле коаксиальной пары.

Результирующее магнитное поле коаксиальной пары представлено на рисунке 1.1, где показаны также напряженности магнитного поля H_φ^а и H_φ^б каждого проводника (а и б) в отдельности. В металлической толще проводника а магнитное поле Н_φ^а= I/2πr, где r – расстояние от центра проводника. Поле Н_φ^бпроводника б вне его выражается таким же уравнением, как и для сплошного проводника: Н_φ^б=I/2πr, где r – расстояние от центра полого проводника. Поэтому при определении внешних магнитных полей коаксиального кабеля параметр r для проводников а и б принимается одинаковым и исчисляется от центра проводников (нулевой точки).

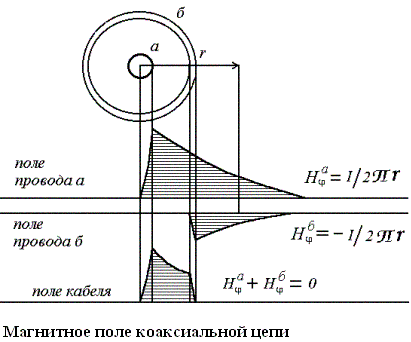
Рис 1.1

Учитывая, что точки в проводниках а и б равны по величине и обратны по знаку, магнитные поля внутреннего и внешнего проводников H_φ^а и H_φ^б в любой точке пространства вне коаксиальной пары также будут равны по величине и направлены в разные стороны. Следовательно, результирующее магнитное поле вне коаксиальной пары равно нулю:

H_φ = H_φ^а + H_φ^б= (I/2πr) + (-I/2πr) = 0.

Таким образом, силовые линии магнитного поля располагаются внутри коаксиальной пары в виде концентрических окружностей; вне коаксиальной пары магнитное поле отсутствует. Электрическое поле внутри коаксиальной пары также замыкается по радиальным направлениям между проводниками а и б ,а за ее пределами равно нулю.

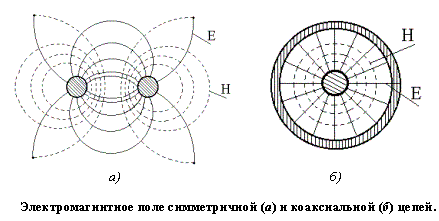
Рис 1.2

На рис.1.2 изображены электромагнитные поля коаксиальной и симметричной цепи. Как видно из рисунка, электромагнитное поле коаксиальной пары полностью замыкается внутри нее, а силовые линии электрического поля симметричной пары действуют на довольно значительном от нее расстоянии. Отсутствие внешнего электромагнитного поля обусловливает основные достоинства коаксиальных кабелей: широкий диапазон частот, большое число каналов, защищенность от помех и возможность организации однокабельной связи. В симметричных цепях из-за наличия внешнего электромагнитного поля возникают вихревые токи в соседних цепях и окружающих металлических массах (свинцовой или алюминиевой оболочке, экране и т.д.) и часть энергии рассеивается в виде потерь на тепло.

3.2. Первичные параметры коаксиальной цепи

В отличие от проводников, где имеются свободные электроны и действует ток проводимости І_пр, в диэлектрике нет свободных электронов, а имеются ионы и связанные диполи. Под действием переменного электромагнитного поля в диэлектрике происходит смещение диполей, их переориентация и поляризация.

Поляризацией называется смещение положительных и отрицательных зарядов в диэлектрике под действием электрического поля. Переменная поляризация обусловливает возникновение и действие токов смещения – емкостных токов І_см и вызывает затраты энергии на переориентацию диполей (потери в диэлектрике). Чем выше частота колебаний, тем сильнее токи смещения и больше потери. При постоянном токе эти явления отсутствуют.

Явления в диэлектрике полностью характеризуются двумя параметрами: емкостью С, определяющей способность поляризации и величину токов смещения, и проводимостью G, определяющей величину потерь в диэлектрике. Емкость кабеля аналогична емкости конденсатора, где роль обкладок выполняют проводники, а диэлектриком служит расположенный между ними изоляционный материал или воздух. При определении емкости коаксиального кабеля учитывают, что он аналогичен цилиндрическому конденсатору и его электрическое поле создается двумя цилиндрическими поверхностями с общей осью. Вследствие осевой симметрии напряженность электрического поля имеет равные потенциалы на определенном расстоянии от центра кабеля.

Проводимость изоляции G может быть определена как составляющая потерь в диэлектрике конденсатора, емкость которого эквивалентна емкости кабеля (рис. 2.1).

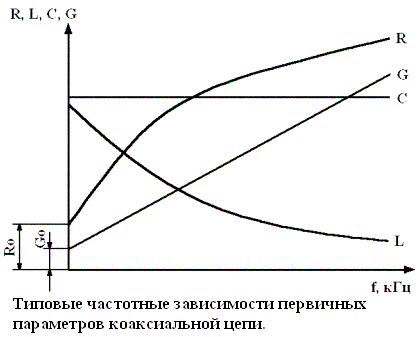
Рис 2.1

Проводимость изоляции и емкость коаксиального кабеля могут быть рассчитаны по формулам. Емкость C=2πε_a/ln(r_b/r_a), Ф/м. Проводимость изоляции G=2πσ/ln(r_b/r_a), См/м.

Обычно принято проводимость изоляции G выражать через тангенс угла диэлектрических потерь в изоляции кабеля

tg δ=G/ωC=σ/ωε_a.

Тогда G = [2π/ln(r_b/r_a)] ωε_a tg δ = ωC tg δ.

Заменяя в выражении емкости ε_а=ε₀ε_r , получим для 1 км кабеля (где ε₀=10^-9/(36π), Ф/м)

C=ε_r10^-6/[18ln(r_b/r_a)].

Соответственно

G=ωC tg δ, Cм/км,

Тип кабеля	Тип изоляции	εэ	Отношение υд/υв	tg δэ 10-4 при частоте, МГц
				1	5	10	60
2,6/9,5	Полиэтиленовая шайба	1,13	8,8	0,5	0,5	0,7	0,8
2,6/9,5	Полиэтиленовая спираль	1,1	6	0,4	0,4	0,5	0,6
1,2/4,6	Баллонно-полиэтиленовая	1,22	9	1,2	1,3	1,5	―
2,1/9,7	Пористо-полиэтиленовая	1,5	50	2	3	3	―
5/18	Кордельно-стирофлексная	1,19	12	0,7	0,8	1,0	1,2

где ε_r и tg δ – δиэлектрическая проницаемость и тангенс угла диэлектрических потерь изоляции. Эффективность значения ε_э и tg δ_э комбинированной изоляции, применяемой в коаксиальных кабелях, приведены в таблице.

В общем виде, кроме проводимости изоляции, обусловленной диэлектрическими потерями G, необходимо учитывать также проводимость, обусловленную утечкой тока в силу несовершенства изоляции: G=1/R_из. По величине эта проводимость изоляции обратно пропорциональна сопротивлению изоляции кабеля. В коаксиальных кабелях R_из нормируется величиной 10 000 МОм·км. Таким образом, проводимость изоляции коаксиального кабеля, G=1/R_из+ωC·tgδ, См/км. По абсолютной величине в используемом диапазоне частот второй член существенно больше первого, поэтому 1/R_из можно не учитывать.

Проанализируем полученные результаты и рассмотрим зависимости первичных параметров коаксиального кабеля. На рис.2.1 приведены частотные зависимости параметров коаксиального кабеля

Из рисунка видно, что с тостом частоты активное сопротивление закономерно возрастает за счет поверхностного эффекта и эффекта близости. Причем наибольшее удельное значение имеет сопротивление внутреннего проводника: величина R_а больше R_б в 3-4 раза. Индуктивность с увеличением частоты уменьшается. Это обусловлено уменьшением внутренней индуктивности проводников L_а и L_б за счет поверхностного эффекта. Внешняя индуктивность L_вш не меняется с изменением частоты. Емкость не зависит от частоты. Проводимость изоляции с ростом частоты линейно возрастает. Величина ее зависит в первую очередь от качества диэлектрика, используемого в кабеле и характеризуемого величиной угла диэлектрических потерь tg δ.

3.3. Вторичные параметры передачи коаксиальной цепи

Коаксиальные кабели практически используются в спектре частот от 60 кГц и выше, где R<<ωL и G<<ωC. Поэтому вторичные параметры передачи их рассчитываются по следующим формулам:

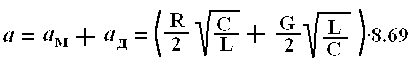
где а_м – коэффициент затухания вследствие потерь в металле; а_д – коэффициент затухания вследствие потерь в диэлектрике.

Однако вторичные параметры передачи коаксиальных кабелей целесообразно выражать непосредственно через габаритные размеры (d и D) и параметры изоляции(ε и tg δ).

Коэффициент затухания а, дБ/км, находится при подстановке в формулу первичных параметров. Для кабеля с медными проводниками получим:

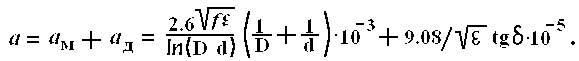
При замене медных проводников на алюминиевые затухание возрастает пропорционально соотношению активных сопротивлений или соответствий обратно пропорционально корню квадратному или проводимостей металлов

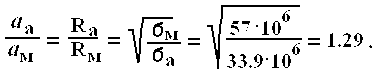
т.е. затухание коаксиального кабеля с алюминиевыми проводниками больше, чем с медными, на 29%.

При замене только внешнего проводника на алюминиевый затухание возрастает в соотношении

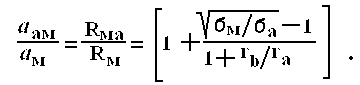
При соотношении радиусов проводников r_b/r_a=3.6 получим

а_ма/а_м=R_ма/R_м=1.06,

т. е. Затухание кабеля возрастает всего на 6%.

Изложенное дает основание сделать вывод о целесообразности применения коаксиальных кабелей с внешним алюминиевым проводником. В этом случае затухание увеличивается всего на 6%, а расход меди на изготовление коаксиального кабеля сокращается на 65%.

Потери в металле а_и изменяются пропорционально , а потери в диэлектрике а_д связаны с частотой линейным законом и с увеличением ƒ

Возрастают значительно быстрее (Рис.3.1).

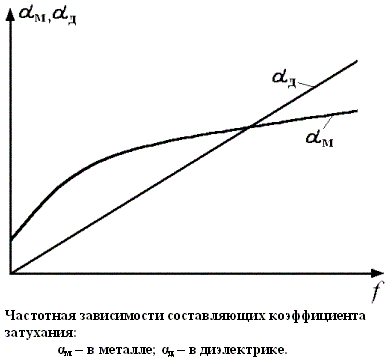
Рис 3.1

При использовании высококачественных диэлектриков (с малым tg δ) можно добиться в определенном частотном диапазоне очень малых диэлектрических потерь и положить а_д=0. при очень высоких частотах они настолько возрастут, что величина а_д играет значительную роль в общем затухании кабеля. В практически используемом спектре частот передачи по коаксиальным кабелям (до 60·10⁶ Гц) при современных кабельных диэлектриках величина а_д незначительна (не превышает 2-3% а_м) и затухание увеличивается примерно пропорционально .

Коэффициент фазы β, рад/км, коаксиальной пары определяется из уравнения . Подставляя сюда значения L и C, получим . Коэффициент фазы можно выразить также через С и , рад/км, где С – скорость света равная 300 000 км/с.

Скорость распространения υ, км/с, электромагнитной энергии по коаксиальным парам

.

Коэффициент сдвига фаз определяет длину волны в кабеле:

Из приведенных формул видно, что коэффициент фазы возрастает с увеличением частоты прямолинейно. Это обусловливает почти полное постоянство скорости передачи энергии по коаксиальному кабелю во всем рассматриваемом спектре частот. Скорость передачи уменьшается с увеличением диэлектрической проницаемости. Так, при сплошной полиэтиленовой изоляции (ε_r=2.3) с=200 000 км/с, а при воздушно комбинированной изоляции коаксиальной пары (ε_r=1.1), с=285 000 км/с.

Скорость передачи энергии по коаксиальным парам выше, чем по симметричным, и почти приближается к скорости распространения электромагнитных волн в воздухе (300 000 км/с).

Волновое сопротивление Ζ_в, Ом, коаксиальной пары для высоких частот определяется выражением

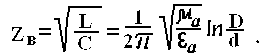
или

где - волновое сопротивление диэлектрика.

Имея в виду, что μ_а=μ₀μ_r и α_a=ε₀ε_r ,где μ₀=4π·10^-7, Гн/м, и ε₀=10^-9/36π, Τ/м, получим

где - волновое сопротивление воздушного пространства. Для среды μ_r=1 получим

В коаксиальных парах со сплошным диэлектриком (ε_r=2.3) Ζ_B=50 Ом, а при комбинированной изоляции (ε_r=1.1) величина волнового сопротивления составляет примерно 75 Ом.

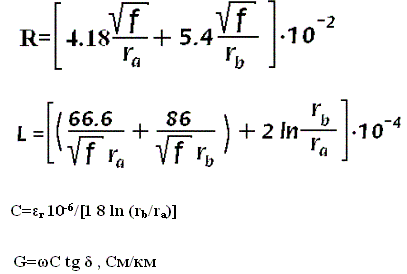
Формулы