При исследовании условий самовозбуждения и стационарного режима работы автогенератора принимались во внимание следующие обстоятельства. При самовозбуждении амплитуда нарастающих колебаний в автогенераторе мала и работа генератора происходит на линейном участке ВАХ транзистора i_к = F(u_к), на котором крутизна транзистора является постоянной величиной, не зависящей от напряжения u_oc, т. е. . В этом случае дифференциальное уравнение автогенератора (15.8) становится линейным.

В стационарном режиме, когда амплитуды гармонического колебания на контуре автогенератора U_m. и гармонического колебания обратной связи U_m.. являются установившимися, средняя крутизна в уравнении (15.8) является также постоянной величиной и дифференциальное уравнение автогенератора снова можно считать линейным:

.

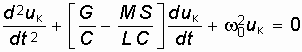Из решения этого уравнения определялись условия самовозбуждения, амплитуда и частота генерируемых колебаний.

При анализе переходного режима автогенератора, когда амплитуды колебаний напряжения на контуре и напряжения обратной связи изменяюется от очень малых величин U_m.(0) и U_m..(0), вызванных флуктуационными процессами в автогенераторе, до установившихся значений, считать крутизну постоянной уже невозможно; дифференциальное уравнение автогенератора (15.8) является нелинейным. Поскольку способов точного аналитического решения нелинейного дифференциального уравнения второго порядка не существует воспользуемся для его решения приближенным методом медленно меняющихся амплитуд (ММА).

Метод ММА применяется для решения нелинейных дифференциальных уравнений с малым параметром. Этот метод введен в радиотехнику впервые Ван-дер-Полем, который рассмотрел ряд задач, связанных с установлением колебаний в ламповых генераторах и других колебательных системах. В дальнейшем этот метод получил обоснование в работах академиков Л.И. Мандельштама, Н.Д. Папалекси, А.А. Андронова и их учеников. Особо следует отметить работы академиков Н.Н. Боголюбова, Н.М. Крылова, а также Ю.А. Митропольского, посвященные развитию и метода ММА (или, как он часто называется, метода укороченных уравнений).

Поскольку в автогенераторах для повышения стабильности частоты генерируемых колебаний и подавления высших гармоник тока коллектора, являющихся продуктом нелинейности ВАХ транзистора, используется высокодобротный контур (Q 1), то амплитуда напряжения на контуре, а также амплитуда напряжения обратной связи, изменяются так медленно, что их приращение за время периода колебаний T много меньше самой амплитуды колебаний . Это условие "малости" изменения амплитуды колебаний и будет использовано для анализа переходных процессов в автогенераторе.

Покажем, что указанное условие "малости" изменения амплитуды колебаний в автогенераторе, , действительно выполняется при больших добротностях контура Q. Напряжение на колебательном контуре автогенератора изменяется по закону

,

где – коэффициент затухания контура; U₀ – начальное значение амплитуды колебаний, вызванное флуктуациями тока в транзисторе; w ₀ – частота свободных колебаний в контуре.

Введем обозначение

и перепишем выражение для u(t):

где U_m(t) – описывает закон изменения амплитуды автоколебаний во времени.

Продифференцировав (15.25), найдем скорость изменения амплитуды

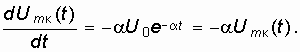
Перепишем (15.26) в приращениях

Пусть отрезок времени D t = T, тогда . Если a T 1, то условие выполняется. Чтобы убедиться в этом, выразим декремент затухания a T параллельного контура через добротность Q:

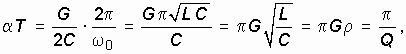
где – добротность контура; r – характеристическое сопротивление контура.

Для контура высокой добротности (Q 1) декремент затухания a T 1, поэтому

,

в чем и требовалось убедиться.

Воспользуется условием (15.29) для перехода от полного дифференциального уравнения автогенератора (15.8) к укороченному.

Перепишем (15.29), разделив правую и левую части неравенства на период колебаний

.

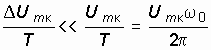Перейдем снова к бесконечно малым приращениям амплитуды колебаний, полагая, что период колебаний достаточно мал по сравнению со временем изменения амплитуды

.

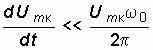Неравенство (15.30) еще более усилится, если правую часть умножим на 2p :

.

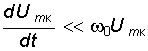Продифференцировав (15.31), получим неравенство для 2-ой производной

.

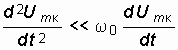Воспользуемся (15.31) и (15.32) для перехода от дифференциального уравнения автогенератора (15.8), составленного относительно напряжения на контуре u_к(t), к дифференциальному уравнению, составленному относительно огибающей амплитуды этого напряжения U_m.(t). Тем самым удастся понизить порядок дифференциального уравнения.

Вычислим первую и вторую производные выражения u_к(t) = и учтем неравенства (15.31) и (15.32):

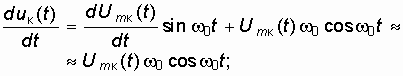
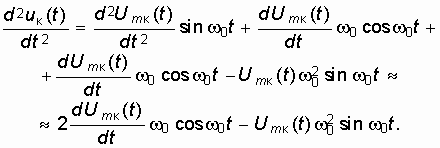
Подставим (15.33) и (15.34) в уравнение автогенератора (15.8):

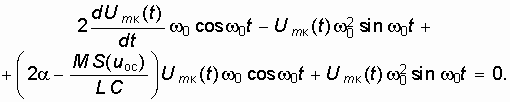
После преобразования этого выражения имеем окончательно:

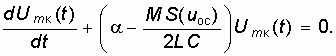
Получили так называемое "укороченное" нелинейное дифференциальное уравнение 1-го порядка для медленно меняющейся амплитуды колебаний, или уравнение Ван-дер-Поля.

Таким образом, использование условий медленности изменения амплитуды позволило перейти от мгновенных значений напряжения на контуре u_к к амплитудным U_m. и понизить порядок уравнения. Заметим, что уравнение (15.35) по-прежнему остается нелинейным, так как в него входят мгновенная крутизна ВАХ, зависящая от мгновенного напряжения u_ос. Однако, от мгновенной крутизны можно перейти к средней крутизне в силу того, что в высокодобротном контуре можно пренебречь высшими гармониками. Тогда уравнения (15.35) можно переписать в виде

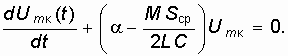
Это уравнение, строго говоря, также является нелинейным (так как средняя крутизна зависит от амплитуды); однако в таком уравнении первого порядка можно разделить переменные и получить его решение.

Для решения уравнения (15.36) прежде всего нужно выбрать выражение для средней крутизны. Если аппроксимировать ВАХ транзистора полиномом

и считать, что , то можно найти амплитуду первой гармоники тока

и среднюю крутизну по первой гармонике

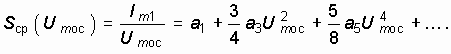
Это общее выражение для средней крутизны пригодно для расчета переходных процессов в автогенераторе как в мягком, так и в жестком режимах, но сложность расчетов при этом резко возрастает. Поэтому для практических расчетов используют не полиномиальную аппроксимацию, а аппроксимацию гиперболическим тангенсом.

Среднюю крутизну транзистора для мягкого режима самовозбуждения с достаточной для практических расчетов степенью точности можно аппроксимировать функцией

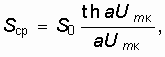
где S₀ – начальное значение крутизны S(0); , S – значение крутизны в рабочей точке, I_н – ток насыщения транзистора.

Подставив выражение для крутизны (15.37) в укороченное уравнение для огибающей амплитуды колебаний автогенератора (15.36) и вынося коэффициент затухания a за скобки, получим:

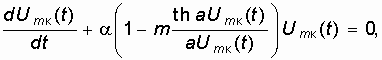
где ; .

Получим решение уравнения (15.38) для двух отрезков времени:

– режим малых амплитуд, когда аргумент . В это случае и уравнение (15.38) будет линейным однородным дифференциальным уравнением 1-го порядка:

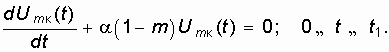
– режим больших амплитуд , тогда и (15.38) будет линейным неоднородным дифференциальным уравнением 1-го порядка

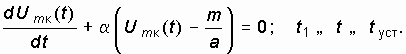
Решение уравнения (15.39) имеет вид:

где U_m.(0) – начальное значение амплитуды колебаний в момент t = 0 (на первом интервале времени ), обусловленное флуктуациями в транзисторе. Из (15.41) видно, что амплитуда колебаний будет увеличиваться, если m > 1, т. е. M > M_кр или .

Для решения (15.40) проведем разделение переменных и проинтегрируем

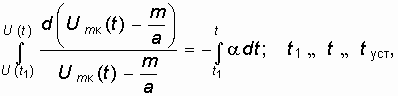
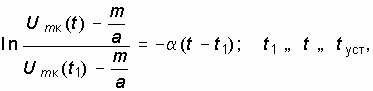
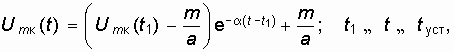
где U_m.(t₁) – начальное значение амплитуды колебаний на втором интервале , равное конечному значению амплитуды на первом интервале .

При получим установившееся решение для амплитуды колебаний

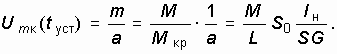
Из (15.43) видно, что установившееся колебание не зависит от начальных условий, а зависит от величины обратной связи , проводимости контура G и характеристик транзистора.

Время установления колебаний в автогенераторе находится из условия, что амплитуда колебаний изменяется от U_m.(0) до 0,95 от установившегося решения, т. е. . Откуда имеем

.

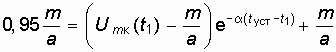Начальное значение амплитуды колебаний U_m.(t₁) найдем из выражения средней крутизны на первом интервале S_ср = S и на втором интервале . Отсюда:

.

Из (15.45) находим

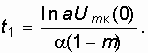
Подставив (15.46) в (15.44), получим

;

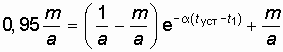Откуда находим

Из (15.47) видно, что длительность установления колебаний t_уст зависит от начальной амплитуды U_m.(0), коэффициента затухания a , величины обратной связи m и параметра транзистора a. С увеличением начальной амплитуды колебаний U_m.(0) время установления уменьшается.

Пример. Рассчитать время установления колебаний в автогенераторе для следующих условий: величина взаимной индукции в два раза больше критической ; начальное значение амплитуды колебаний в 100 раз меньше амплитуды колебаний в середине переходного процесса U_m.(0) = , добротность контура Q = 100.

Выразим в (15.47) коэффициент затухания a контура через добротность Q: , тогда из (15.47) получим

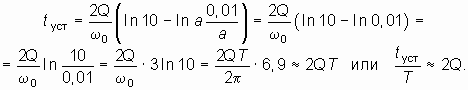
При Q = 100 установление колебаний происходит за 200 периодов.