Рассмотрение методов спектрального анализа радиотехнических сигналов мы начнем с детерминированных периодических сигналов. Как уже подчеркивалось выше детерминированные сигналы характеризуются тем, что в любой наперед заданный момент времени его значения можно точно определить. Периодическим детерминированным сигналом является сигнал известной формы периодически повторяющийся через интервал времени , называемый периодом повторения. Математически периодический сигнал описывается выражением

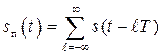, (2.1)

К периодическим сигналам относятся гармоническое колебание, определенное на бесконечном интервале времени, последовательность импульсов с известной амплитудой, длительностью и периодом повторения и другие.

Спектральный анализ предусматривает выбор системы базисных функций. На практике наибольшее распространение получили тригонометрические функции. Это обусловлено тем, что при преобразовании сигналов такой формы, например, линейными радиотехническими цепями их форма сохраняется, а меняются только амплитуда и фазы колебаний. С другой стороны, формирование таких сигналов осуществляется достаточно простыми техническими средствами.

Сигналы, описываемые тригонометрическими функциями, называются гармоническими сигналами, а спектральный анализ в системе базисных тригонометрических функций – гармоническим анализом.

Итак, выберем в качестве базисных функций систему

, (2.2)

где .

Нетрудно убедиться, что функции, образующие систему (2.2) являются ортогональными на интервале времени и удовлетворяют условию периодичности (2.1). Тогда в соответствии с (1.36) можно записать

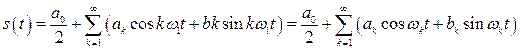, (2.3)

где .

Нормы базисных функций в соответствии с (1.26) равны

; .

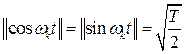Тогда из (1.39) вытекает

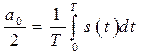, (2.4)

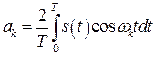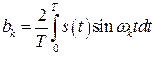, . (2.5)

Выражение (2.3) называется тригонометрическим рядом Фурье и представляет собой разложение сигнала на составляющие в системе тригонометрических функций.

В радиотехнической практике часто оказывается удобнее иное представление ряда (2.3). Выделим из (2.3) k-тую составляющую

и представим ее в виде

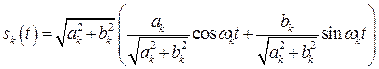, (2.6)

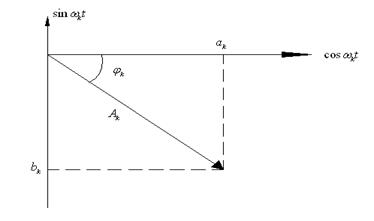
Рис. 2.1

С геометрической точки зрения составляющую можно рассматривать как вектор в системе координат (рис. 2.1). Длина вектора , а -угол, на который повернут вектор относительно оси . Нетрудно убедиться, что

, .

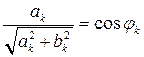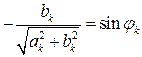Тогда выражение (2.6) принимает вид

, (2.7)

где .

С учетом (2.7), ряд Фурье (2.3) можно переписать следующим образом

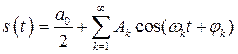. (2.8)

Составляющая

(2.9)

называется k-той гармонической составляющей или просто k-той гармоникой.

В соответствии с определением спектра, данном в предыдущем разделе, совокупность и составляют амплитудный спектр, а совокупность – фазовый спектр сигнала. Таким образом, амплитудный спектр периодического сигнала содержит постоянную составляющую и бесконечное число амплитуд соответствующих гармоник. То же самое относится и к фазовому спектру.

При спектральном анализе спектры удобно представлять в виде спектральных диаграмм.

На рис.2.2, а изображен периодический сигнал в координатах и . Проведем еще одну ось, перпендикулярную осям и и отложим на этой оси значения . Изобразим гармонические составляющие сигнала на этих частотах, а на оси частот отложим значения и в виде отрезков прямой. Если теперь развернуть всю систему координат вокруг оси на 90º в направлении стрелки, мы получим диаграмму амплитудного спектра сигнала (рис. 2.2, б). Таким же образом можно построить спектральную диаграмму фазового спектра, примерный вид которой показан на рис. 2.2, в.

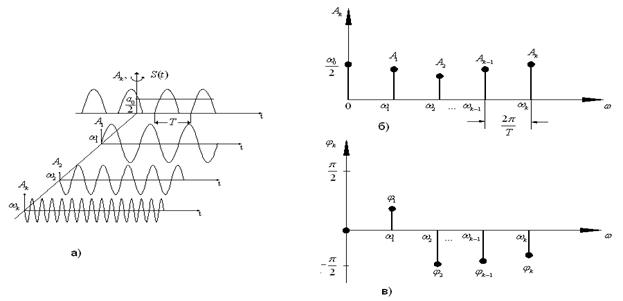
Рис. 2.2