11.1. Нахождение реакции нелинейной резистивной цепи на заданное воздействие
11.2. Режим малых колебаний в нелинейных электрических цепях
11.3. Воздействие гармонического колебания на нелинейный резистивный элемент
11.4. Резонансное усиление и умножение частоты колебаний
11.5. Выпрямление гармонических колебаний
11.6. Ограничение мгновенных значений гармонических колебаний
11.7. Воздействие суммы гармонических колебаний на нелинейный резистивный элемент
11.1. Нахождение реакции нелинейной резистивной цепи на заданное воздействие
Для нахождения реакции нелинейной электрической цепи с нелинейным двухполюсником или четырехполюсником на заданное воздействие можно использовать графические построения. Статические характеристики нелинейного прибора, т. е. зависимость между воздействием и реакцией на его внешних зажимах для режима постоянного тока, считаются известными. Ими могут быть, например, вольт-амперная характеристика нелинейного резистора, или зависимость между постоянными напряжениями на входе и выходе нелинейного четырехполюсника и др. Эти характеристики находятся, как правило, в результате измерений и представляются в виде графических зависимостей, что и оправдывает использование графических методов решения рассматриваемой задачи.
В основе метода лежит предположение о том, что в любой момент времени реакция нелинейного прибора на подведенное к нему воздействие будет такой же, как и его реакция на постоянное воздействие той же величины. Иными словами, предполагается, что модель анализируемой цепи является моделью резистивной электрической цепи. Ниже на примере рассматривается методика графического нахождения реакции нелинейного прибора с однозначной характеристикой нелинейности.
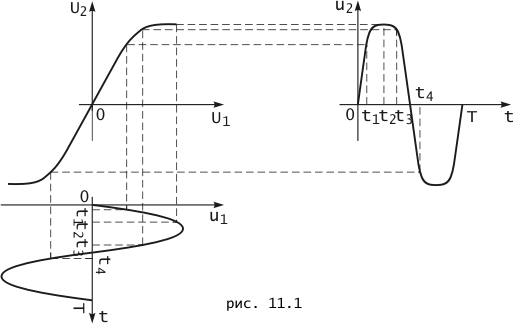
Рассмотрим зависимость постоянного напряжения U 2 на выходе нелинейного четырехполюсника от постоянного напряжения U 1, подведенного к его входу. Ее график U 2 = U 2(U 1) показан па Рис. 11.1 рис. 11.1. На этом же рисунке, приведен график воздействия u 1(t). Он повернут на угол ![]() по часовой стрелке по сравнению с общепринятым графическим изображением функции времени. Воздействие в примере тождественно равно нулю вне интервала 0 < t < T, внутри которого оно описывается функцией u 1(t) = U msin(2 pt /T).
по часовой стрелке по сравнению с общепринятым графическим изображением функции времени. Воздействие в примере тождественно равно нулю вне интервала 0 < t < T, внутри которого оно описывается функцией u 1(t) = U msin(2 pt /T).
В момент времени t = t 1 ко входу нелинейного прибора, как это следует из рис. 11.1., подводится напряжение u 1(t ), т. е. при t = t1 : U1 = u 1 (t 1 ). Напряжение на его выходе, которое находится по графику U 2 (U 1 ), т. е. напряжение U 2 при U1 = u 1 (t 1 ) и будет напряжением реакции u 2 (t 1 ) нелинейного при6oрa в момент времени t 1 . Значение реакции отложено на графике u 2 (t), приведенном на том же рисунке. Отсчетные значения u1 (t1 )и u2 (t1 ) соединены на рис. 11.1. штриховой линией. Аналогичные построения приведены на рисунке и для трех других моментов времени t = t2 , t = t3 , t = t4 . В результате подобных построений и находится график реакции u2 (t).
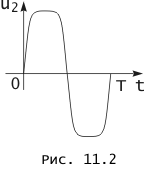
Сопоставление графиков воздействия u 1(t ) и реакции u 2(t ), приведенных на рис. 11.1., показывает, что они отличаются друг от друга формой. Следовательно, в рассматриваемой нелинейной электрической цепи произошло искажение формы реакции по сравнению с формой воздействия, обусловленное нелинейностью характеристики используемого нелинейного прибора. Из тех же графиков следует, что указанные искажения уменьшаются с уменьшением амплитуды воздействия и для любого t при условии | u1 (t)| < u1 (t1 ), зависимость реакции от воздействия будет близка к линейной. Итак, анализируемую цепь в ряде случаев можно рассматривать как линейную электрическую цепь и с тем большим основанием, чем меньше амплитуда воздействия. Наоборот, с увеличением амплитуды воздействия заметнее отличия формы реакции от формы воздействия. В частности, значение реакции u 2(t) по абсолютной величине практически не зависит от воздействия, если | u1 (t)| > u1 (t2 ) (см. рис. 11.1. ), а при | u 1 (t)| = u 1 (t 2 ) реакция принимает вид двух трапецеидальных импульсов различной полярности. Ее график показан на рис. 11.2.
|
|
|
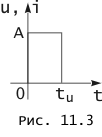
Искажение формы реакции относительно формы воздействия свойственно электрическим цепям и с другими характеристиками нелинейности, отличающимися от рассмотренных в примере, в том числе и многозначными. Вместе с тем в рассматриваемых резистивных нелинейных цепях не искажается форма воздействия в виде импульса прямоугольной формы, график которого приведен на рис. 11.3. Здесь нелинейность проявляется в отсутствии прямой пропорциональности между амплитудами реакции и воздействия, а при больших амплитудах воздействия – в независимости их друг от друга.
Естественно, что если характеристика нелинейности задана аналитически, то реакция нелинейного прибора на заданное воздействие может быть найдена и в результате численного решения нелинейного уравнения, связывающего мгновенные значения реакции и воздействия в выбранной совокупности дискретных моментов времени.
11.2. Режим малых колебаний в нелинейных электрических цепях
Линейные функциональные узлы современной радиоэлектронной аппаратуры, в частности, усилители самого разнообразного назначения, содержат то или иное число, часто весьма значительное, транзисторов, операционных усилителей и других полупроводниковых или электронных приборов. Между тем характеристики перечисленных приборов в широком интервале изменения воздействий относятся к числу нелинейных.
Убедимся в принципиальной возможности построения цепей (двухполюсников, четырехполюсников, многополюсников) с линейными (близкими к линейным) характеристиками, хотя в их составе имеются приборы с нелинейными характеристиками.
Рассматриваемые активные цепи с полупроводниковыми или электронными приборами содержат источники постоянного напряжения, необходимые для "питания" этих приборов. При отсутствии других воздействий в цепи устанавливается режим постоянного тока. В рассматриваемых цепях рабочие точки располагаются на тех участках характеристик, в пределах которых последние могут считаться линейными. На рис. 11.4 это точка с координатами U0, I0. Такие участки всегда можно выделить на характеристиках приборов.
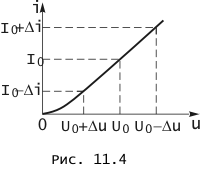
Выбор рабочей точки в каждом из используемых нелинейных приборов определяет и рабочие участки характеристик этих приборов, Здесь под рабочим участком нелинейной характеристики понимается тот ее участок, включающий рабочую точку, в пределах которого характеристика может быть аппроксимирована одной прямой. Обычно рабочая точка располагается в середине рабочего участка характеристики.
Пусть, далее, к цепи подведено воздействие u0(t), изменяющееся по любому закону, такое, при котором напряжения (токи) в нелинейных устройствах цепи не выходят за пределы их рабочих участков. Реакция цепи на рассматриваемое воздействие выражается в изменениях (приращения х) напряжений и токов в устройствах цепи по сравнению с их значениями в режиме постоянного тока.
Приращения напряжений D uk(t) и токов D ik(t) в к- й ветви цепи (k=1, 2, ..., n) связаны между собой линейными соотношениями в силу линейности используемых рабочих участков характеристик нелинейных приборов и, следовательно, по отношению к указанным приращениям цепь может рассматриваться как линейная. Постоянные же напряжения и токи обуславливают необходимый режим работы нелинейных приборов, их рабочие точки. В связи с этим на схемах замещения нелинейных цепей, используемых как линейные, цепи постоянного тока не изображаются, а приращения напряжений и токов относительно их начальных значений, обусловленные приложенным к цепи внешним напряжением (током), называются просто напряжениями и токами и обозначают их соответствующими строчными буквами uk(t), ik(t).
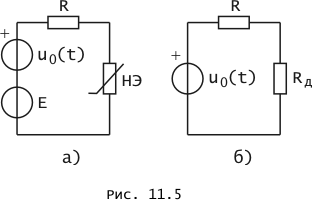
Рассмотрим простейший пример. На рис. 11.5, а приведена схема цепи, содержащей нелинейный резистивный элемент, источник постоянного напряжения Е, линейный резистор с сопротивлением R и источник с задающим напряжением u0(t). Рабочая точка нелинейного резистора находится так, как это изложено в § 10.2. Приращения напряжения D u и тока D i на внешних зажимах нелинейного резистора связаны соотношением D i = GдD u, если вольт-амперная характеристика нелинейного резистора может считаться линейной в окрестности его рабочей точки. Действительно, при этом условии отношение D i/D u не отличается от его предела при D u Ю 0, т. е. от дифференциальной проводимости нелинейного резистора в его рабочей точке. Поэтому последний можно заменить в схеме замещения анализируемой цепи линейным резистором с проводимостью Gд. В соответствии с этим на рис. 11.5, б изображена схема линейной электрической цепи, пригодная для нахождения реакции исходной цепи на воздействие u0(t).
Линейность характеристик цепей с нелинейными полупроводниковыми и электронными приборами может быть существенно повышена за счет применения ряда схемных решений (отрицательная обратная связь, двухтактное включение нелинейных приборов и др.).
Нелинейные электрические цепи, у которых при ограниченных по величине воздействиях реакции являются линейными функциями воздействия, часто называют нелинейными электрическими цепями в режиме малых колебаний. Малыми они называются потому, что по абсолютной величине не могут выходить за пределы линейных участков вольт-амперных характеристик используемых нелинейных приборов. Термин этот условен, поскольку для решения задач техники радиосвязи используются нелинейные цепи в режиме малых колебаний с мощностями сигналов в десятки и сотни киловатт.
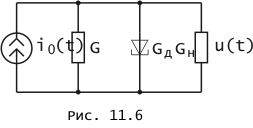
Хорошим примером использования прибора с нелинейной вольт-амперной характеристикой для линейного усиления сигналов в режиме малых колебаний может служить усилитель на туннельном диоде. ВАХ последнего была приведена на рис. 10.1. Идеализированная схема замещения усилителя, рассматриваемого как резистивная электрическая цепь, изображена на рис. 11.6. На ней показаны источник усиливаемого сигнала с задающим током i0(t) и внутренней проводимостью G, проводимость нагрузки Gн и туннельный диод. Рабочая точка диода выбирается на ниспадающем участке его вольт-амперной характеристики (см. рис. 10.1, в), для чего в усилителе имеются цепи питания диода от источника постоянного напряжения, не показанные на схеме.
Пусть напряжение сигнала на зажимах диода не будет выходить за пределы линейного участка его вольт-амперной характеристики в окрестности рабочей точки. Дифференциальная проводимость Gд диода в его рабочей точке отрицательна и при сделанных допущениях может считаться постоянной, т. е. Gд <0 и Gд = const. При этом напряжение сигнала, развиваемое на зажимах нагрузки
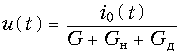
будет, во-первых, линейно связано с задающим током i0(t) источника сигналов, и, во-вторых, при Gд <0 превышать то, которое было бы в отсутствии диода, т. е. при Gд = 0.
Возрастает и мгновенная мощность сигнала в нагрузке ![]() .Оба последних соотношения и свидетельствуют о линейном усилении сигнала в рассматриваемой цепи. Естественно, что эффект усиления обусловлен введением в цепь энергии от источника питания туннельного диода. Последний лишь управляет расходом энергии источника питания в точном соответствии с изменением сигнала во времени. Усилители на туннельных диодах применяются в технике сверхвысоких частот.
.Оба последних соотношения и свидетельствуют о линейном усилении сигнала в рассматриваемой цепи. Естественно, что эффект усиления обусловлен введением в цепь энергии от источника питания туннельного диода. Последний лишь управляет расходом энергии источника питания в точном соответствии с изменением сигнала во времени. Усилители на туннельных диодах применяются в технике сверхвысоких частот.
11.3. Воздействие гармонического колебания на нелинейный резистивный элемент
Постановка задачи анализа
Пусть к нелинейному резистивному элементу подведено гармоническое колебание ![]() и постоянное напряжение смещения U0, т. е. пусть
и постоянное напряжение смещения U0, т. е. пусть ![]() . Ток в элементе может быть найден по вольт-амперной характеристике элемента i = F(u) и является функцией времени i(t).
. Ток в элементе может быть найден по вольт-амперной характеристике элемента i = F(u) и является функцией времени i(t).
График тока i(t) может быть найден с помощью простейших построений, которые иллюстрируются на рис. 11.7. Данные этого рисунка показывают, что реакция i(t) и воздействие u(t) могут существенно отличаться по форме.
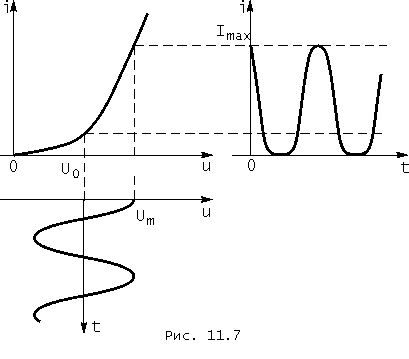
Искажения формы сигнала, обусловленные нелинейностью характеристик электрической цепи, называются нелинейными искажениями.
При воздействии ![]() , подведенном к нелинейному элементу, ток i(t) в элементе будет периодической функцией времени, которая может быть представлена рядом Фурье в форме (5.9) :
, подведенном к нелинейному элементу, ток i(t) в элементе будет периодической функцией времени, которая может быть представлена рядом Фурье в форме (5.9) :
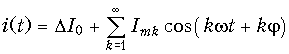 .
.
Следовательно, ток в нелинейном элементе содержит постоянную составляющую D I0, гармоническое колебание с частотой w и начальной фазой j воздействия и гармонические колебания с частотами, кратными частоте воздействия (гармоники колебания). Начальные фазы гармоник кратны начальной фазе воздействия.
Появление гармоник в составе тока в элементе обусловлено нелинейностью его вольт-амперной характеристики, в связи с чем их часто называют продуктами нелинейности.
В соответствии с изложенным спектр амплитуд тока в нелинейном элементе при гармоническом воздействии на элемент является дискретным. Такими же будут спектры напряжений и токов в тех ветвях цепи, которые не подсоединены непосредственно к источнику гармонического воздействия.
В устройствах, используемых в режиме малого сигнала, нелинейные искажения носят паразитный характер и строго нормируются. Для их оценки обычно используется коэффициент нелинейности
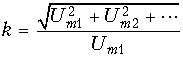 ,
,
где Um1 – амплитуда колебания основной частоты (частоты воздействия), a Um2, Um3, ... – амплитуды гармоник напряжения на выходных зажимах устройства. Так, в высококачественных системах звуковоспроизведения коэффициент нелинейности не превышает долей одного процента.
Ниже рассматриваются аналитические методы вычисления спектров амплитуд колебаний в нелинейных резистивных электрических цепях для различных функций, аппроксимирующих вольт-амперную характеристику нелинейного элемента.
Спектр реакции при полиномиальной характеристике нелинейного элемента
Пусть в окрестности рабочей точки (U0, I0) вольт-амперная характеристика нелинейного элемента описывается полиномом степени n:
![]()
При гармоническом воздействии, когда ![]() ,
,
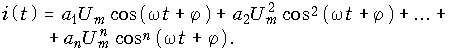
Для нахождения спектра амплитуд реакции тока i(t) в нелинейном элементе удобно вместо общего метода разложения периодической функции i(t) в ряд Фурье воспользоваться выражениями степеней функции coska через функции кратных дуг, согласно которым:
![]()
![]()
![]()
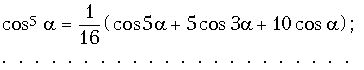
Тогда, полагая ![]() и осуществляя группировку коэффициентов при функциях одинаковых аргументов, преобразуем выражение для i(t) к виду
и осуществляя группировку коэффициентов при функциях одинаковых аргументов, преобразуем выражение для i(t) к виду
![]()
где:
![]()
![]()
![]()
![]()
![]()
![]()
Анализ полученных выражений показывает, что при полиномиальной вольт-амперной характеристике нелинейного элемента и гармоническом воздействии на НЭ:
- Число гармонических составляющих реакции (гармоник) конечно и равно степени полинома, поскольку при n > 2:
![]()
- Амплитуда Im1 первой гармоники колебания при n > 2 в общем случае нелинейно зависит от амплитуды Umприложенного воздействия.
- Амплитуды четных (нечетных) гармоник определяются только коэффициентами при четных (нечетных) степенях слагаемых полинома.
- Изменяется на величину D I0 постоянная составляющая тока.
Спектр реакции при линейно-ломаной характеристике нелинейного элемента
Пусть на одном из участков ВАХ нелинейного элемента монотонно возрастает по закону, близкому к линейному, а на другом, когда элемент "заперт", может считаться равной нулю. Пусть, далее, между ними расположен небольшой по сравнению с первым участок, в котором одна из указанных характеристик переходит в другую. Примером может служить усредненная анодно-сеточная характеристика мощного пентода, приведенная на рис. 11.8, где iА – анодный ток; uСК – напряжение между сеткой и катодом. Пусть, наконец, мгновенные значения напряжения на выходе нелинейного элемента изменяются в пределах всех трех участков его характеристики.
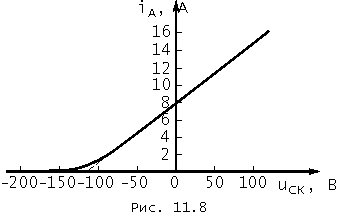
При сформулированных условиях рассматриваемую нелинейную характеристику можно и целесообразно аппроксимировать линейно-ломаной зависимостью, изображенной на рис. 10.32, б. Напряжение "излома" этой зависимости Uотс находится обычно как точка пересечения обоих линейных участков характеристики. Так, на рис. 11.8 Uотс = - 120 В.
Решим задачу спектрального анализа колебаний в нелинейном элементе с рассматриваемой линейно-ломаной вольт-амперной характеристикой, если ко входу элемента подведено напряжение ![]() . Закон изменения тока в элементе может быть, как и ранее, найден с помощью графических построений. Они приведены на рис. 11.9 и показывают, что искомый ток представляет собой периодическую последовательность импульсов, отличающихся от нуля в интервалах
. Закон изменения тока в элементе может быть, как и ранее, найден с помощью графических построений. Они приведены на рис. 11.9 и показывают, что искомый ток представляет собой периодическую последовательность импульсов, отличающихся от нуля в интервалах ![]() (k = 0, ±1; ±2; ...).
(k = 0, ±1; ±2; ...).
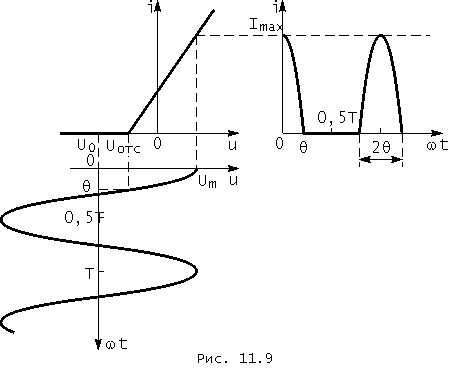
Форма одиночного импульса в интервале ![]() описывается в обозначениях рис. 11.9, как легко убедиться, функцией
описывается в обозначениях рис. 11.9, как легко убедиться, функцией
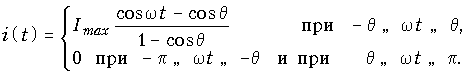
Действительно, при w t = 0 ток i(0) = Imax, при w t = ±q i(t) = = 0, а в интервале ![]() функция i(t) изменяется как ограниченная снизу (отсеченная) косинусоида.
функция i(t) изменяется как ограниченная снизу (отсеченная) косинусоида.
Угол q называется углом отсечки. При гармоническом воздействии ![]() угол отсечки определяет в интервале
угол отсечки определяет в интервале ![]() нижнюю (w t = - q ) и верхнюю (w t = q ) границы временного интервала, в котором ток в элементе отличен от нуля. Поскольку на границах интервала
нижнюю (w t = - q ) и верхнюю (w t = q ) границы временного интервала, в котором ток в элементе отличен от нуля. Поскольку на границах интервала ![]() (см. рис. 11.9), то
(см. рис. 11.9), то
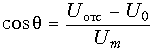 .
.
Пределы изменения угла отсечки заключены между q = 0, когда нелинейный элемент заперт, и q = p (q = 180° ), когда ограничение снизу отсутствует, т. е. когда элемент используется в линейном режиме.
Для нахождения спектра амплитуд рассматриваемой периодической последовательности разложим ее в ряд Фурье. Тогда, опуская промежуточные выкладки, находим следующие выражения:
для постоянной составляющей тока
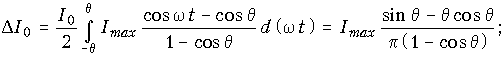 (11.5, а)
(11.5, а)
для амплитуды первой (основной) гармоники
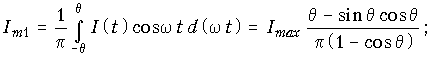
(11.5, б)
для второй гармоники
 (11.5, в)
(11.5, в)
Эти выражения можно было бы получить как частные случаи существующей общей формулы для амплитуды k-й гармоники
![]()
На рис. 11.10 приведены графики тока и спектра амплитуд тока, соответствующие углу отсечки q = p /3.
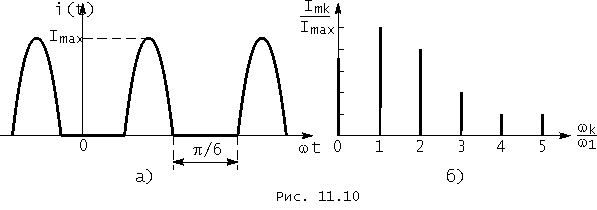
Постоянная составляющая и амплитуды гармоник тока в элементе являются функциями угла отсечки. Обычно они выражаются в относительных единицах
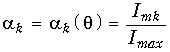
и называются коэффициентами А.И. Берга. Их графики приведены на рис. 11.11 для k Ф 3.
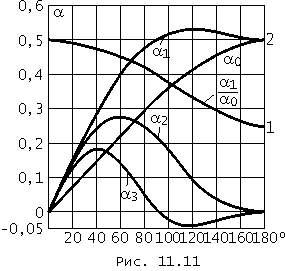
Анализ установленных соотношений показывает, что при линейно-ломаной характеристике нелинейного элемента и гармоническом воздействии на него:
- Число гармонических составляющих реакции бесконечно велико, хотя амплитуды некоторых из них при определенных значениях угла отсечки могут быть равны нулю.
- В общем случае амплитуды гармоник нелинейно зависят от амплитуды гармонического воздействия в силу нелинейного характера зависимости угла отсечки от Um.
- В частном случае, когда рабочая точка U0 совмещена с точкой излома характеристики Uотс, т. е. когда угол отсечки равен p /2, амплитуды гармоник оказываются прямо пропорциональными амплитуде Um гармонического воздействия, поскольку при этом условии величина Imax прямо пропорциональна Um, а угол отсечки согласно (11.4) не изменяется с изменением Um.
Выражение (11.6) является достаточно громоздким для выполнения вычислений. Из (11.7) следует, что
![]()
Выражая величину Imax через амплитуду Um напряжения на НЭ, крутизну S вольт-амперной характеристики и угол отсечки q
![]()
получим более компактную формулу для расчета амплитуд гармоник тока:
![]()
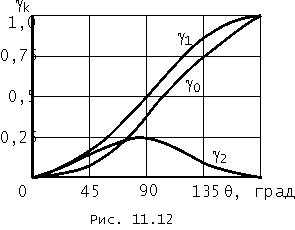
где ![]() – функции Берга.
– функции Берга.
Графики нескольких таких функций представлены на рис. 11.12.
Пример. Считая, что диод обладает идеализированной характеристикой, определить U0, при котором в спектре напряжения UR(t) отсутствует 3-я гармоника, если ![]() (рис. 11.13, а).
(рис. 11.13, а).
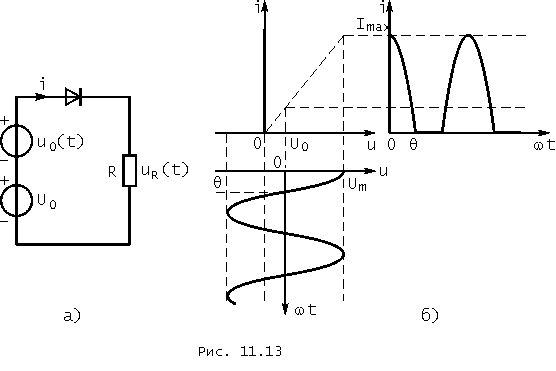
Напряжение на сопротивлении R создают гармоники тока. Выражение для амплитуды k-той гармоники тока при кусочно-линейной аппроксимации НЭ имеет вид (11.6):
![]()
Приравнивая в этом выражении амплитуду 3-й гармоники нулю Im3 = 0, получим
![]()
Учитывая, что
![]()
![]()
перепишем (11.9) в виде
![]()
![]()
Учитывая, что ![]() , получим
, получим
![]() ;
;
![]() ;
; ![]() ;
; ![]() ,
,
что выполняется при ![]() (рис. 11.13, б).
(рис. 11.13, б).
11.4. Резонансное усиление и умножение частоты колебаний
Резонансное усиление в режиме малого сигнала
В радиопередающих и радиоприемных устройствах широко используются для усиления узкополосных сигналов* так называемые резонансные усилители, ламповые и транзисторные. У таких усилителей в качестве нагрузки анода (коллектора, стока) используется параллельный колебательный контур.
Упрощенная схема лампового резонансного усилителя приведена на рис. 11.14, а, а его схема замещения для режима малого сигнала – на рис. 11.14, б. На этих рисунках Eс и Eа – постоянные напряжения сеточного и анодного источников питания.
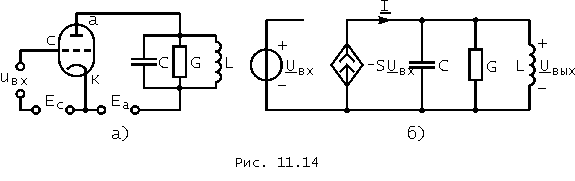
Частотная зависимость комплексного коэффициента усиления усилителя ![]() прямо пропорциональна характеристике контура Z(jw), поскольку в обозначениях рис. 11.14
прямо пропорциональна характеристике контура Z(jw), поскольку в обозначениях рис. 11.14 ![]() ,
, ![]() и, следовательно,
и, следовательно,
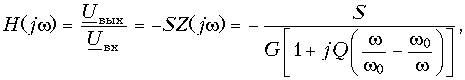
где ![]() – резонансная частота контура и
– резонансная частота контура и ![]() его добротность.
его добротность.
График типовой амплитудно-частотной характеристики усилителя приведен на рис. 11.15.
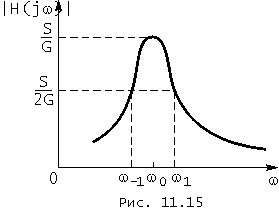
Резонансная частота колебательного контура принимается равной средней частоте усиливаемого узкополосного сигнала, чем достигается его избирательное усиление и подавление помех, если их спектры по частоте достаточно удалены от резонансной частоты контура. Ширина же полосы пропускания контура ![]() выбирается в результате компромисса между требованиями к селективности амплитудно-частотной характеристики контура и допустимыми искажениями спектра усиливаемого сигнала.
выбирается в результате компромисса между требованиями к селективности амплитудно-частотной характеристики контура и допустимыми искажениями спектра усиливаемого сигнала.
Резонансные усилители в режиме малого сигнала находят широкое применение в радиоприемных устройствах, где мощности усиливаемых узкополосных сигналов невелики, поэтому малы, как мощности, потребляемые усилителем от источников питания, так и их роль в формировании общей мощности, расходуемой радиоприемным устройством.
Резонансное усиление в режиме большого сигнала
Для увеличения амплитуды и мощности усиленного сигнала в качестве рабочего используется также и нелинейный участок характеристики усилительного прибора резонансного усилителя, что достигается увеличением амплитуды входного воздействия и выбором соответствующей рабочей точки. Иными словами, усилитель используется в режиме большого сигнала.
В силу нелинейности рабочего участка вольт-амперной характеристики используемого электронного прибора в составе его тока появляются помимо колебания с частотой воздействия, т. е. первой (основной) гармоники, высшие гармоники колебания: вторая и последующие. Если частота воздействия совпадает с резонансной частотой колебательного контура (близка к ней), то амплитуды напряжений, создаваемых на зажимах контура высшими гармониками колебания, могут считаться пренебрежимо малыми по сравнению с амплитудой напряжения первой гармоники, поскольку модуль сопротивления контура на частоте k-й гармоники меньше резонансного сопротивления контура ![]() в число раз, равное
в число раз, равное
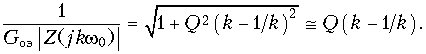
Так, при Q = 100 и k = 2: |Z(j2w 0)| @ |Z(jw 0)|/150. К тому же амплитуды высших гармоник тока обычно меньше амплитуды его первой гармоники.
Итак, можно считать, что в установившемся режиме гармоническому напряжению на входе резонансного усилителя, работающего в режиме большого сигнала, соответствует гармоническое же выходное напряжение. Естественно, что это заключение справедливо для гармонических воздействий, частоты которых находятся в пределах рабочей полосы частот усилителя, т. е. близки к резонансной частоте контура.
При анализе процессов в резонансном усилителе, например, ламповом, пренебрежем влиянием анодного напряжения на анодный ток лампы и будем считать, что анодно-сеточная характеристика лампы является линейно-ломаной (см. рис. 11.8).
Крутизну этой характеристики в ее линейно-возрастающей части обозначим через S. При гармоническом воздействии максимумы импульсов анодного тока лампы Imax связаны с амплитудой воздействия Umвх соотношением
![]() (11.11)
(11.11)
поскольку ![]() , а согласно (11.4) U1 –
, а согласно (11.4) U1 –![]() .
.
Используя соотношения (11.11) и (11.5, б), находим следующие выражения для амплитуды Im1 первой гармоники тока в анодной цепи лампы и амплитуды Umвых с частотой воздействия на зажимах колебательного контура усилителя
![]() ,
,
![]() .
.
Для того чтобы амплитуды гармонической реакции Umвых и гармонического воздействия Umвх линейно зависели одна от другой, в последнем выражении угол отсечки q не должен изменяться с изменением амплитуды воздействия, что согласно (11.4) возможно при U0 = Uотс, когда q = p /2. Итак, при q = p /2
![]()
и, следовательно, резонансный усилитель, работающий в режиме большого сигнала, т. е. в существенно нелинейном режиме, по отношению к его двум парам внешних зажимов может рассматриваться как линейный активный четырехполюсник – усилитель с коэффициентом усиления H(jw ) = 0,5S|Z(jw )|.
В технике радиопередающих устройств резонансные усилители, работающие в режиме большого сигнала, используются как для усиления узкополосных сигналов, так и для усиления гармонических колебаний большей мощности. Оценим коэффициент полезного действия усилителя (КПД) – отношение средней мощности P1 = = 0,5UтвыхЧ Im1, развиваемой усилителем в его колебательном контуре при w = w 0, к мощности ![]() потребляемой усилителем от источника анодного питания
потребляемой усилителем от источника анодного питания
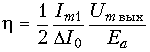 .
.
В этом выражении отношение ![]() может быть доведено до значения, близкого к единице, а отношение
может быть доведено до значения, близкого к единице, а отношение ![]() является функцией угла отсечки. Обращаясь к формулам (11.5), имеем при Umвых = Ea
является функцией угла отсечки. Обращаясь к формулам (11.5), имеем при Umвых = Ea
![]()
Если усилитель используется для усиления узкополосных сигналов, угол отсечки, как было показано, должен быть равен p / 2, чему, согласно (11.12), соответствует ![]() , а практически
, а практически ![]() . Следует учитывать также, что при
. Следует учитывать также, что при ![]() усилитель не расходует энергии в паузах сигнала.
усилитель не расходует энергии в паузах сигнала.
Заметим, что при работе усилителя в режиме малого сигнала, т. е. когда мгновенные значения воздействия не выходят за пределы возрастающего участка линейно-ломаной характеристики лампы (транзистора), коэффициент полезного действия h < 0,5.
При использовании резонансного усилителя в режиме большого сигнала для усиления гармонического колебания неизменной амплитуды, когда важно лишь сохранение формы воздействия, угол отсечки может отличаться от p / 2. Исследование функции (11.12) показывает, что ее значения монотонно возрастают от значения h = 0,5 при q = p до единицы при q ® 0. Практически малые значения угла отсечки и значения КПД усилителя, близкие к единице, не могут быть достигнуты по ряду причин. Обычно в резонансных усилителях указанного назначения h = 0,85...0,9.
Резонансное умножение частоты колебаний
Резонансный усилитель в режиме большого сигнала используется и для генерации гармонического колебания, частота которого кратна частоте гармонического воздействия. Резонансная частота колебательного контура w 0 подобного резонансного умножителя частоты совпадает с частотой выделяемой гармоники анодного (коллекторного, стокового) тока. Она создает на зажимах контура с резонансным сопротивлением ![]() гармоническое напряжение с частотой w 0 = kw и амплитудой
гармоническое напряжение с частотой w 0 = kw и амплитудой ![]() . По сравнению с ней амплитуды напряжения остальных гармоник, включая и первую, должны быть пренебрежительно малы. Для этого используются контуры высокой добротности и выбирается такой угол отсечки, при котором амплитуда выделяемой гармоники тока принимает максимальное значение. Так, амплитуда второй гармоники тока максимальна (см. рис. 11.10) при q = 60° , третьей – при q = 40° и т. д. Максимальные значения амплитуд гармоник тока убывают с ростом порядкового номера гармоники, что ограничивает возможные области практического применения резонансных умножителей частоты. Обычно кратность умножения не выше трех.
. По сравнению с ней амплитуды напряжения остальных гармоник, включая и первую, должны быть пренебрежительно малы. Для этого используются контуры высокой добротности и выбирается такой угол отсечки, при котором амплитуда выделяемой гармоники тока принимает максимальное значение. Так, амплитуда второй гармоники тока максимальна (см. рис. 11.10) при q = 60° , третьей – при q = 40° и т. д. Максимальные значения амплитуд гармоник тока убывают с ростом порядкового номера гармоники, что ограничивает возможные области практического применения резонансных умножителей частоты. Обычно кратность умножения не выше трех.
11.5. Выпрямление гармонических колебаний
Для питания полупроводниковых и электронных приборов активных электрических цепей необходимо постоянное питающее напряжение. С этой целью используются преобразователи химической энергии в энергию электрическую (гальванические элементы, аккумуляторы), термоэлектрические преобразователи (термоэлементы, солнечные батареи), а также выпрямители – устройства, преобразующие гармоническое напряжение в напряжение знакопостоянное с теми или иными допустимыми флюктуациями относительно его среднего значения.
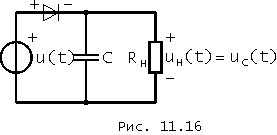
Схема простейшего выпрямителя приведена на рис. 11.16. Если к этой нелинейной цепи подвести гармоническое воздействие, то спустя определенное время в ней установятся периодические колебания, которые, естественно, не будут гармоническими. Постоянная составляющая напряжения на зажимах резистивной нагрузки выпрямителя этих периодических колебаний и представляет собой выпрямленное постоянное напряжение. Гармоники же колебания оказывают мешающее действие на работу питаемых устройств. Для снижения их уровня в рассматриваемый простейший выпрямитель введен конденсатор. Емкость конденсатора выбирается такой, чтобы его сопротивление на частотах гармоник, начиная с первой, было бы значительно меньше сопротивления нагрузки выпрямителя, т. е. чтобы (1/w С) < Rн или w CRн <1. Ясно, что чем сильнее неравенство, т. е. чем больше постоянная времени t = RнC превышает период Т = 2p /w гармонического воздействия, тем меньше амплитуды гармоник напряжения на зажимах нагрузки, обусловленных гармониками тока.
При выбранных на рис.11.16 положительных направлениях напряжений в силу однонаправленного характера проводимости диода напряжение uc(t) на зажимах нагрузки будет создаваться лишь положительными полуволнами выпрямляемого напряжения. Следовательно, и напряжение на конденсаторе всегда будет положительным.
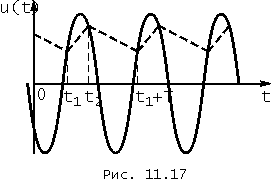
Пусть в установившемся режиме колебаний в момент времени t1 (см. рис. 11.17) периодически изменяющееся воздействие u(t)![]() достигает, возрастая, напряжения заряженного конденсатора uc(t1), т. е. пусть u(t1) = uc(t1). С этого момента времени uд > 0, диод открывается и начинается заряд (подзаряд) конденсатора. Он длится до тех пор, пока напряжение на зажимах конденсатора не сравняется в момент времени t2 (см. рис. 11.17) с убывающим после максимума напряжением воздействия. После этого, пока t2 < t < t1 + Т, диод оказывается закрытым (uд < 0) и конденсатор разряжается на сопротивление R. Следовательно, в указанном интервале времени напряжение на зажимах конденсатора (нагрузки) убывает по закону
достигает, возрастая, напряжения заряженного конденсатора uc(t1), т. е. пусть u(t1) = uc(t1). С этого момента времени uд > 0, диод открывается и начинается заряд (подзаряд) конденсатора. Он длится до тех пор, пока напряжение на зажимах конденсатора не сравняется в момент времени t2 (см. рис. 11.17) с убывающим после максимума напряжением воздействия. После этого, пока t2 < t < t1 + Т, диод оказывается закрытым (uд < 0) и конденсатор разряжается на сопротивление R. Следовательно, в указанном интервале времени напряжение на зажимах конденсатора (нагрузки) убывает по закону
![]()
Затем процесс периодически повторяется с периодом воздействия T. График uc(t) приведен на рис. 11.18. Среднее значение выпрямленного напряжения U0 равно среднему значению функции uc(t), т. е.
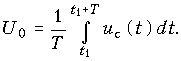
Разность же uc(t)—U0 определяет закон изменения во времени суммы гармоник напряжения на зажимах нагрузки выпрямителя – "пульсацию" выпрямленного напряжения. О ней можно судить по отношению наибольшего и наименьшего значений напряжения, равного
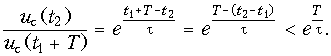
Так, при t = 10T и t2—t1 = 0,25T это отношение не превышает 1,08, а значит наибольшие и наименьшие значения напряжения на выходе выпрямителя отличаются не более, чем на 8 %.
Величина выпрямленного напряжения существенно зависит от соотношения между параметрами генератора, диода и нагрузки. Для приближенной оценки постоянной составляющей выпрямленного напряжения положим, что вольт-амперная характеристика диода имеет вид, показанный на рис. 11.19.
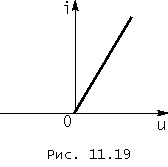
Сопротивление диода при uд > 0 с учетом резистивного внутреннего сопротивления генератора, обозначим через Rд. Положим, далее, что флюктуации напряжения относительно его постоянной составляющей U0 пренебрежимо малы, т.е. будем считать, что uс(t) @ U0 = const. O допустимости этого предположения, которое потребуется выполнять на практике, можно судить по приведенному выше примеру.
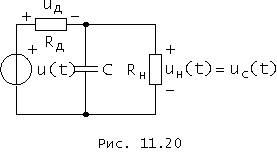
При указанных допущениях ток через диод в цепи, схема которой для uc(t) = U0 приведена на рис. 11.20, представляет собой периодическую последовательность импульсов, подобную показанной на рис. 11.10, а.

Графические построения, иллюстрирующие процессы в анализируемой цепи, показаны на рис. 11.21. Из них следует, что
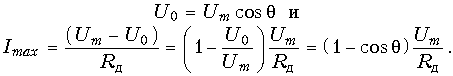
Этому значению максимума тока соответствует согласно (11.10, а) постоянная составляющая тока
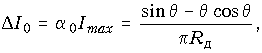
протекающего через диод и нагрузку.
Заменяя в этом выражении D I0 на U0/Rн и учитывая, что ![]() , находим зависимость между углом отсечки и сопротивлением диода и нагрузки:
, находим зависимость между углом отсечки и сопротивлением диода и нагрузки:
![]()
Решив это трансцендентное уравнение, определяем неизвестный пока угол отсечки q , как функцию отношения сопротивлений Rд/Rн, а затем и величину выпрямленного постоянного напряжения ![]() .
.
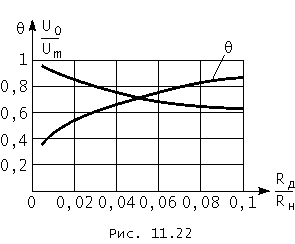
На рис. 11.22 приведен в относительных единицах график зависимости выпрямленного постоянного напряжения U0/Um от сопротивления диода Rд/Rн. Данные рисунки показывают, что при (Rд/Rн) ![]() 1 величина постоянного напряжения близка к амплитуде выпрямляемого гармонического напряжения и убывает при прочих равных условиях с увеличением сопротивления диода. Чаще всего (Rд/Rн) < 0,1, когда U0 < 0,65Um, иначе КПД выпрямителя становится недопустимо малым. На том же рисунке показан график зависимости угла отсечки в радианах от того же отношения Rд/Rн. При (Rд/Rн) < 0,1 угол отсечки не превышает 0,87 рад, т. е. 50° , и убывает с уменьшением отношения (Rд/Rн).
1 величина постоянного напряжения близка к амплитуде выпрямляемого гармонического напряжения и убывает при прочих равных условиях с увеличением сопротивления диода. Чаще всего (Rд/Rн) < 0,1, когда U0 < 0,65Um, иначе КПД выпрямителя становится недопустимо малым. На том же рисунке показан график зависимости угла отсечки в радианах от того же отношения Rд/Rн. При (Rд/Rн) < 0,1 угол отсечки не превышает 0,87 рад, т. е. 50° , и убывает с уменьшением отношения (Rд/Rн).
Рассмотренные простейшие выпрямители называются однополупериодными, поскольку у них при формировании выпрямленного напряжения используется энергия только одного из каждой пары полупериодов выпрямляемого гармонического напряжения, а, точнее, его части.
Схема двухполупериодного выпрямителя мостового типа изображена на рис. 11.23. Здесь за счет поочередного открытия диодов, помеченных на рисунке четными и нечетными индексами, достигается постоянство знака тока в нагрузке выпрямителя для обоих полупериодов выпрямляемого напряжения. Именно двухполупериодные выпрямители нашли преимущественное применение для выпрямления однофазного гармонического напряжения. Качественные и количественные оценки процессов в двухполупериодных выпрямителях можно получить прямым обобщением таковых в выпрямителях однополупериодных.
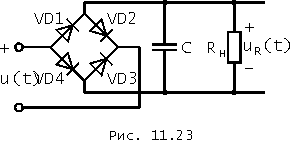
Для более полного подавления гармоник, если в этом возникает необходимость, в выпрямитель вводятся в дополнение к конденсатору один или два реактивных элемента, образующие фильтр нижних частот с необходимым ослаблением на частотах гармоник. Задача фильтрации гармоник двухполупериодного выпрямителя облегчается тем, что у него амплитуда пульсаций выпрямленного напряжения вдвое меньше, а их частота вдвое выше, чем у выпрямителя однополупериодного при прочих разных условиях. В бытовой радиоэлектронной аппаратуре вместо фильтра в дополнение к конденсатору существенное подавление гармоник осуществляет включенный на выходе выпрямителя стабилизатор напряжения – устройство для поддержания постоянства напряжения на его выходе при изменении сопротивления его нагрузки.
11.6. Ограничение мгновенных значений гармонических колебаний
Нелинейный четырехполюсник, предназначенный для ограничения мгновенных напряжений сигнала, называется ограничителем.
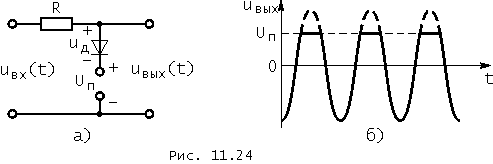
Схема простейшего ограничителя с ограничением сверху приведена на рис. 11.24, а. В ограничитель входят линейный резистор с сопротивлением R, выпрямительный диод и генератор постоянного напряжения с задающим пороговым напряжением Uп. На первом этапе анализа процессов в рассматриваемом ограничителе будем считать, во-первых, что диод идеален, т. е. его сопротивление или бесконечно велико, если uд < 0, или равно нулю, если uд > 0, и во-вторых, что внутреннее сопротивление генератора постоянного напряжения равно нулю.
Если при указанных предположениях напряжение на зажимах диода будет отрицательным, т. е. когда uвх(t) < Uп, диод будет "закрыт" и напряжение на выходе ограничителя будет равно напряжению на его входе, т. е. uвых(t) = uвх(t). Если же uвх(t) > Uп, диод "открывается", его сопротивление становится равным нулю. Тем самым источник постоянного напряжения подключается к выходу ограничителя и напряжение на выходе ограничителя будет равно задающему напряжению источника Uп на протяжении всего времени пока uвх > Uп. Итак:
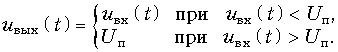
Соответствующая графическая иллюстрация приведена на рис. 10.24, б для воздействия в виде гармонического колебания ![]() . Штриховой линией на рисунке показаны "отсеченные" ограничителем участки входного колебания.
. Штриховой линией на рисунке показаны "отсеченные" ограничителем участки входного колебания.
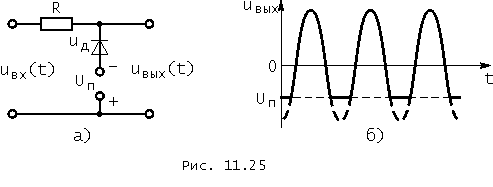
На рис. 11.25, а изображена схема ограничителя с ограничением снизу. Аналогичные рассуждения показывают, что у такого ограничителя при тех же, что и выше, допущениях:
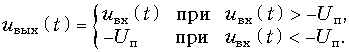
График напряжения на выходе ограничителя с ограничением снизу для того же, гармонического, воздействия изображен на рис. 10.25, б.
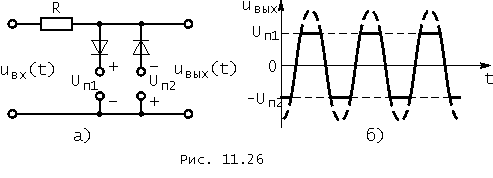
Наконец, на рис. 11.26, а приведена схема ограничителя с двухсторонним ограничением, у которого для принятых допущений
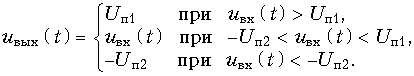
Обычно ограничители с двухсторонним ограничением имеют как симметричные, так и асимметричные пределы ограничений.
Напряжение на выходе ограничителя с симметричными пределами ограничения, если к его входу подается гармоническое напряжение ![]() , по форме близко к периодической последовательности импульсов трапециедальной формы и чередующейся полярности (см. рис. 11.2). Форма импульсов приближается к прямоугольной по мере усиления неравенства Um> Uп1 = Uп2.
, по форме близко к периодической последовательности импульсов трапециедальной формы и чередующейся полярности (см. рис. 11.2). Форма импульсов приближается к прямоугольной по мере усиления неравенства Um> Uп1 = Uп2.
Если рассматриваемую периодическую последовательность импульсов подвести к устройству, моделирующему операцию дифференцирования, то напряжение на его выходе будет представлять собой периодическую последовательность коротких импульсов чередующейся полярности. Форма каждого отдельного импульса близка к прямоугольной; его длительность тем меньше, а высота тем больше, чем больше амплитуда гармонического колебания превышает порог ограничения.
В заключение заметим, что задачу анализа колебаний в ограничителе можно решать с учетом реальных характеристик диодов и конечного внутреннего сопротивления генераторов. При этом качественно картина процессов в ограничителе практически сохранится без изменений по сравнению с рассмотренной выше.
11.7. Воздействие суммы гармонических колебаний на нелинейный резистивный элемент
Спектральный состав тока при бигармоническом воздействии
Пусть к нелинейному резистивному элементу подведено бигармоническое воздействие, т. е. колебание в виде суммы двух гармонических колебаний разных частот и постоянное напряжение смещения U0
![]()
Предположим, что ВАХ нелинейного элемента описывается полиномом
![]()
Тогда ток в цепи НЭ равен:
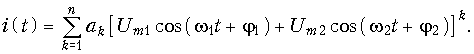
Для анализа спектра тока аппарат рядов Фурье здесь не применим, так как в общем случае функция (11.13) не является периодической. Следует, как и при гармоническом воздействии на НЭ, воспользоваться формулами преобразования тригонометрических функций. При этом
для квадратичного члена суммы (11.13)
![]()
![]()
![]()
![]()
![]()
![]()
для кубичного члена
![]()
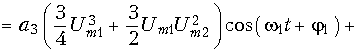
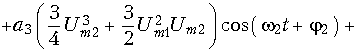
![]()
![]()
![]()
![]()
![]() и т. д.
и т. д.
Допустим, что n = 3, т. е., что вольт-амперная характеристика нелинейного элемента описывается полиномом третьей степени. Тогда полученные выше выражения для i2(t) и i3(t) показывают, что ток в элементе кроме линейной составляющей реакции i1(t) = ![]() содержит также постоянную составляющую, гармонические колебания с частотам воздействия w 1 и w 2 и гармоники колебаний с частотами 2w 1, 2w 2,3w 1 и 3w 2.
содержит также постоянную составляющую, гармонические колебания с частотам воздействия w 1 и w 2 и гармоники колебаний с частотами 2w 1, 2w 2,3w 1 и 3w 2.
Перечисленные составляющие спектра характерны и для воздействия на тот же элемент двух гармонических колебаний с частотами w 1 и w 2 порознь. При совместном же их воздействии в спектре реакции появляются колебания с частотами
|w 1 ± w 2|, |2w 1 ± w 2| и |w 1 ± 2w 2|* .
Соответствующие колебания называются комбинационными, а их частоты - комбинационными частотами. Амплитуды комбинационных колебаний зависят от амплитуд обеих составляющих бигармонического воздействия и в рассматриваемом примере для колебаний с частотами
|w 1 ± w 2|, |2w 1 ± w 2| и |w 1 ± 2w 2|
пропорциональны соответственно произведениям ![]() и
и ![]() .
.
Аналогичные выкладки для остальных членов суммы (11.13) приводят к заключению, что при бигармоническом воздействии на нелинейный элемент с полиномиальной вольт-амперной характеристикой спектр реакции содержит гармонические колебания с частотами
![]()
где l = 0, 1, 2, ..., n; m = 0, 1, 2, ..., n, l + m Ф n.
Сумма l + m определяет порядок комбинационного колебания с частотой (11.14). Так, комбинационные колебания 4-го порядка – это колебание с частотами 4w 1, |3w 1 ± w 2|, |2w 1 ± 2w 2|, |w 1 ± 3w 2| и 4w 2.
Комбинационные частоты при воздействии суммы гармонических колебаний
В общем случае входное воздействие можно представить бесконечной суммой
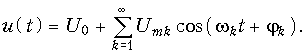
В зависимости от степени n аппроксимирующего полинома в спектре тока, протекающего через нелинейный элемент, появляются комбинационные частоты вида:
![]()
l, m, s, k – целые положительные числа. Например, при воздействии на НЭ с ВАХ в виде полинома второй степени суммы трех гармонических колебаний в спектре тока, помимо постоянной составляющей и первых двух гармоник каждой частоты, присутствуют комбинационные частоты |w 1 ± w 2|; |w 1 ± w 3|; |w 2 ± w 3|. При аппроксимации полиномом третьей степени дополнительно появляются третьи гармоники с частотами 3w 1, 3w 2, 3w 3 и колебания с комбинационными частотами типа |w 1 ± w 2 ± w 3|, |2w 1 ± w 3|, |w 1 ± 2w 3| и т. д.
11.8. Преобразование частоты гармонического колебания
При передаче электрических сигналов на расстояние часто требуется переносить спектр сигнала вверх или вниз по шкале частот. Такой перенос спектра называется преобразованием частоты. Необходимость в преобразовании частот возникает, например, в случаях если спектр сигнала, который нужно передать, расположен на шкале частот значительно ниже полосы пропускания системы передачи.
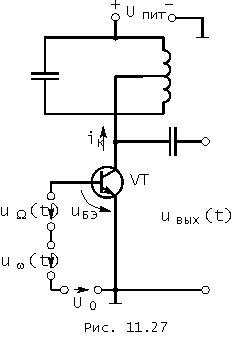
В качестве преобразователя частоты может быть использован усилительный каскад на транзисторе с колебательным контуром (рис. 11.27 ). Предположим, что нужно перенести вверх по шкале частот на значение w гармоническое низкочастотное колебание с частотой W :
![]()
Подадим на вход нелинейного резонансного усилителя, кроме этого колебания, также высокочастотное колебание с частотой w :
![]()
Амплитуды напряжений смещения U 0 , низкочастотного U mW и высокочастотного U mw колебаний выберем так, чтобы работать на участке ВАХ, который достаточно точно аппроксимируется полиномом второй степени
![]()
Напряжение на участке база—эмиттер
![]()
После подстановки этого выражения в зависимость (11.15) в формуле для тока появляются гармонические колебания с частотами W , w , 2W , 2w и с суммарной и разностной комбинационными частотами w + W и w – W .
Колебательный контур резонансного усилителя настроен на частоту w + W и выделяет из спектрального состава тока колебание
![]()
Выделенное колебание тока создает на резонансном сопротивлении контура R 0э падение напряжения
![]()
которое и является выходным сигналом преобразователя частоты.
В реальных системах связи передаваемый низкочастотный сигнал не является гармоническим, а имеет сложный спектр UW (w ) (рис. 11.28 , а), т. е. состоит из суммы гармонических колебаний с частотами W 1 , W 2 , W 3 , ... .
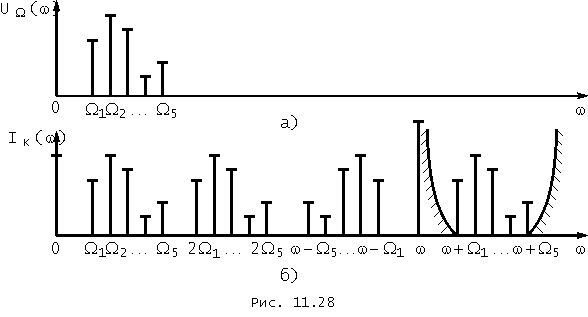
Если этот сигнал вместе с высокочастотным колебанием uw (t) подать на нелинейный элемент, то в спектре тока I К (w ) (рис. 11.28 , б), протекающего через НЭ, будут присутствовать полезные продукты преобразования – комбинационные частоты w + + W 1 , w + W 2 , w + W 3 , ... . Чтобы отфильтровать токи с этими частотами, недостаточно воспользоваться одиночным колебательным контуром, поскольку он не сможет обеспечить хорошую фильтрацию полезных продуктов преобразования. Его можно заменить в схеме рис. 11.27 обычной резистивной нагрузкой, а на выходе схемы включить электрический фильтр с характеристикой ослабления (на рис. 1.28 , б она показана штриховой линией), обеспечивающей необходимую степень подавления несущего колебания с частотой w .
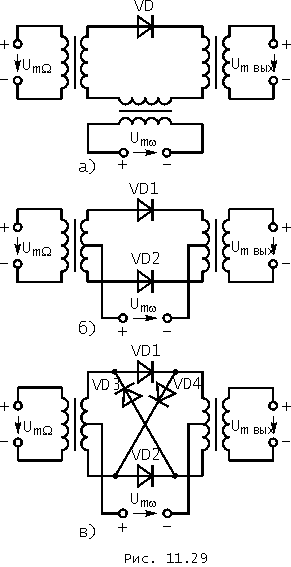
Приведем еще несколько практических схем преобразователей частоты. На рис. 11.29 представлены диодные преобразователи: однотактный (а), двухтактный или балансный (б) и кольцевой (в), работающие в режиме больших амплитуд колебания частоты w, т. е. в режиме аппроксимации ВАХ диодов линейно-ломаными функциями.
В балансных и кольцевых преобразователях гораздо меньше побочных продуктов преобразования; тем самым значительно облегчаются требования к фильтру, выделяющему полезные колебания.
11.9. Вопросы и задания для самопроверки
-
- Каково число гармонических составляющих реакции при полиномиальной аппроксимации ВАХ нелинейного элемента и гармоническом воздействии?
- В чем принципиальное отличие спектров при полиномиальной аппроксимации ВАХ нелинейного элемента при воздействии порознь двух гармонических колебаний с частотами w 1 и w 2 и при совместном их воздействии?
- Что называется углом отсечки и как он зависит от напряжения смещения и амплитуды гармонического воздействия?
- При каком угле отсечки амплитуды гармонических составляющих реакции прямо пропорциональны амплитуде гармонического воздействия и почему?
- Какими коэффициентами при полиномиальной аппроксимации ВАХ определяются амплитуды четных (нечетных) гармоник реакции при гармоническом воздействии? Покажите это на примере.
- При каких условиях в резонансном усилителе, работающем в режиме "большого" сигнала, т. е. в нелинейном режиме, амплитуда реакции и гармонического воздействия имеют линейную зависимость?
- Напишите возможные частоты гармонических составляющих реакции в электрической цепи при аппроксимации ВАХ нелинейного элемента полиномом четвертого порядка при бигармоническом воздействии.
- Как изменяется КПД и выходная мощность резонансного усилителя от угла отсечки?
- На какую частоту настраивают параллельный колебательный контур и каким выбирают угол отсечки в умножителях частоты? Чем ограничена кратность умножения частоты на практике?
- Как изменяется выпрямленное постоянное напряжение U0/Um от отношения сопротивления диода к сопротивлению нагрузки Rд/Rн?
- В чем преимущество двухполупериодного выпрямителя по сравнению с однополупериодным и почему?
- ВАХ нелинейного резистивного элемента аппроксимирована полиномом
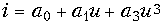 . Найдите частоты всех составляющих тока, если к элементу приложено напряжение: а)
. Найдите частоты всех составляющих тока, если к элементу приложено напряжение: а) 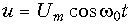 , б)
, б) 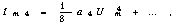 .
.
Ответ: а) 0, w 0, 3w 0; б) 0, w 0, 2w 0, 3w 0.
-
- ВАХ нелинейного резистивного элемента аппроксимирована полиномом
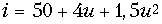 mA. К элементу приложено напряжение
mA. К элементу приложено напряжение 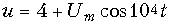 В. Найдите зависимость амплитуды первой гармоники от амплитуды переменной составляющей напряжения Um.
В. Найдите зависимость амплитуды первой гармоники от амплитуды переменной составляющей напряжения Um.
- ВАХ нелинейного резистивного элемента аппроксимирована полиномом
Ответ: ![]() .
.
-
- На нелинейный резистивный элемент с ВАХ
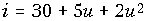 mA действует напряжение
mA действует напряжение 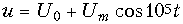 В. Определите зависимость амплитуды первой гармоники тока Im1 от напряжения смещения U0 при фиксированной амплитуде переменной составляющей напряжения Um = 3B.
В. Определите зависимость амплитуды первой гармоники тока Im1 от напряжения смещения U0 при фиксированной амплитуде переменной составляющей напряжения Um = 3B.
- На нелинейный резистивный элемент с ВАХ
Ответ: ![]()
-
- К нелинейному резистивному элементу, ВАХ которого аппроксимирована полиномом
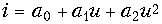 , приложено напряжение
, приложено напряжение 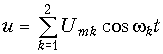 . Найдите амплитуды гармонических составляющих тока.
. Найдите амплитуды гармонических составляющих тока.
- К нелинейному резистивному элементу, ВАХ которого аппроксимирована полиномом
Ответ: ![]() ;
; ![]()
![]()
![]()
![]() .
.
-
- Найдите аналитическое выражение для ВАХ нелинейного элемента, который обеспечивает преобразование синусоидального воздействия x(t) в бесконечную последовательность треугольных импульсов.
Ответ: ![]() - 1 Ф x Ф 1.
- 1 Ф x Ф 1.
-
- К нелинейному резистивному элементу, ВАХ которого описывается полиномом
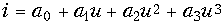 , приложено напряжение
, приложено напряжение 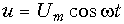 . При каком условии постоянная составляющая тока через элемент не зависит от амплитуды приложенного к нему напряжения?
. При каком условии постоянная составляющая тока через элемент не зависит от амплитуды приложенного к нему напряжения?
- К нелинейному резистивному элементу, ВАХ которого описывается полиномом
Ответ: a2 = 0.