6.8.1. Коды Хэмминга
Коды Хэмминга (Hamming codes) — это простой класс блочных кодов, которые имеют следующую структуру:
![]() , (6.71)
, (6.71)
где т = 2,3,... . Минимальное расстояние этих кодов равно 3, поэтому, согласно уравнениям (6.44) и (6.47), они способны исправлять все однобитовые ошибки или определять все ошибочные комбинации из двух или менее ошибок в блоке. Декодирование с помощью синдромов особенно хорошо подходит к кодам Хэмминга. Фактически синдром можно превратить в двоичный указатель местоположения ошибки [5]. Хотя коды Хэмминга не являются слишком мощными, они принадлежат к очень ограниченному классу блочных кодов, называемых совершенными; их особенности описывались в разделе 6.5.4.
Если предположить, что используется жесткое декодирование, вероятность появления битовой ошибки можно записать с помощью уравнения (6.46).
Здесь р — вероятность ошибочного приема канального символа (вероятность перехода в двоичном симметричном канале). Вместо уравнения (6.72) мы можем использовать другое эквивалентное уравнение (это уравнение (Г. 16), которое выводится в приложении Г).
![]() (6.73)
(6.73)
На рис. 6.21 приведен график зависимости вероятности ошибки в декодированном бите от вероятности ошибки в канальном символе, на котором сравниваются разные блочные коды. Для кодов Хэмминга на графике взяты значения т = 3, 4 и 5 или (n, k) = (7,4), (15,11), (31,26). Для описания гауссового канала с использованием когерентной демодуляции сигналов BPSK, вероятность ошибки в канальном символе можно выразить через ![]() как это было сделано в уравнении (4.79).
как это было сделано в уравнении (4.79).
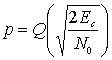 (6.74)
(6.74)
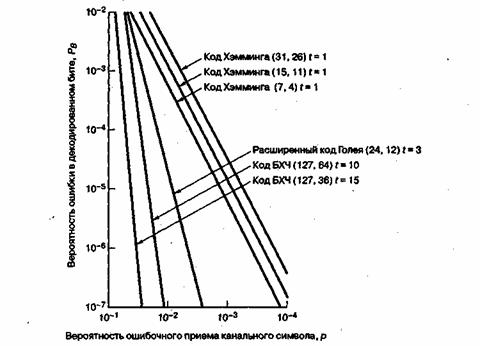
Рис. 6.21. Зависимость вероятности битовой ошибки от вероятности ошибки в канальном символе для нескольких блочных кодов
Здесь ![]() - отношение энергии кодового символа к спектральной плотности мощности шума, a Q(X) определено в уравнении (3.43). Чтобы связать
- отношение энергии кодового символа к спектральной плотности мощности шума, a Q(X) определено в уравнении (3.43). Чтобы связать ![]() с энергией бита информации на единицу плотности спектрального шума (
с энергией бита информации на единицу плотности спектрального шума (![]() ), используем следующее выражение.
), используем следующее выражение.
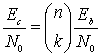 (6.75)
(6.75)
Для кодов Хэмминга уравнение (6.75) принимает следующий вид.
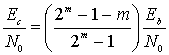 (6.76)
(6.76)
Объединяя уравнения (6.73), (6.74) и (6.76), ![]() при когерентной демодуляции сигналов BPSK в гауссовом канале можно выразить как функцию
при когерентной демодуляции сигналов BPSK в гауссовом канале можно выразить как функцию ![]() . Результаты для различных типов блочных кодов отображены на рис. 6.22. Для кодов Хэмминга взяты следующие значения (n, k) = (7,4), (15,11), (31,26).
. Результаты для различных типов блочных кодов отображены на рис. 6.22. Для кодов Хэмминга взяты следующие значения (n, k) = (7,4), (15,11), (31,26).
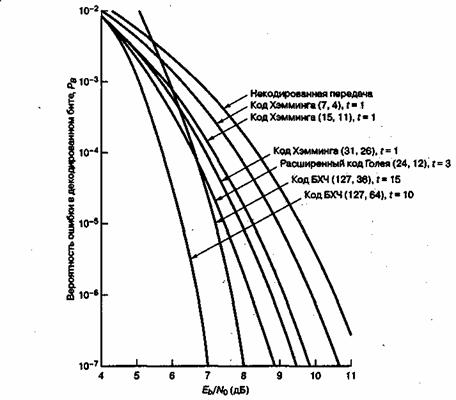
Рис. 6.22. Зависимость ![]() от
от ![]() при когерентной демодуляции сигналов BPSK в гауссовом канале для нескольких блочных кодов
при когерентной демодуляции сигналов BPSK в гауссовом канале для нескольких блочных кодов
Пример 6.11. Вероятность ошибки для модулированных и кодированных сигналов.
Кодированный сигнал с модуляцией BFSK передается по гауссовому каналу. Сигнал некогерентно обнаруживается и жестко декодируется. Найдите вероятность ошибки в декодированном бите, если кодирование осуществляется блочным кодом Хэмминга (7,4), а принятое: значение равно 20.
Решение
Сначала, используя уравнение (6.75), находим ![]() .
.
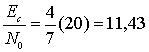
Затем для кодированного некогерентного сигнала BFSK мы можем связать вероятность ошибки в канальном символе с ![]() , подобно тому, как это было сделано в уравнении (4.96).
, подобно тому, как это было сделано в уравнении (4.96).
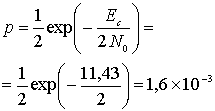
Подставляя этот результат в уравнение (6.73), получаем следующее значение вероятности ошибки в декодированном бите.
![]() ≈
≈![]()
6.8.2. Расширенный код Голея
Одним из наиболее практичных блочных кодов является двоичный расширенный код Голея (extended Golay code) (24, 12), который образован путем прибавления битов четности к совершенному коду (23, 12), известному как код Голея (Golay code). Эти дополнительные биты повышают минимальное расстояние ![]() с 7 до 8, что дает степень кодирования 1/2, реализовать которую проще (с точки зрения системного тактового генератора), чем степень кодирования кода Голея, равную 12/23. Расширенный код Голея значительно мощнее рассмотренного в предыдущем разделе кода Хэмминга. Цена, которую приходится платить за повышение эффективности, заключается в более сложном декодере и, соответственно, более широкой полосе пропускания.
с 7 до 8, что дает степень кодирования 1/2, реализовать которую проще (с точки зрения системного тактового генератора), чем степень кодирования кода Голея, равную 12/23. Расширенный код Голея значительно мощнее рассмотренного в предыдущем разделе кода Хэмминга. Цена, которую приходится платить за повышение эффективности, заключается в более сложном декодере и, соответственно, более широкой полосе пропускания.
Для расширенного кода Голея ![]() , поэтому, исходя из уравнения (6.44), можно сказать, что код гарантирует исправление всех трехбитовых ошибок. Кроме того, декодер можно сконструировать так, чтобы он исправлял некоторые комбинации с четырьмя ошибками. Поскольку исправить можно только 16,7% комбинаций с четырьмя ошибками, декодер, для упрощения, обычно реализуется для исправления только трехбитовых ошибочных комбинаций [5]. Если предположить жесткое декодирование, то вероятность битовой ошибки для расширенного кода Голея можно представить как функцию вероятности p ошибки в канальном символе (см. уравнение (6.46)).
, поэтому, исходя из уравнения (6.44), можно сказать, что код гарантирует исправление всех трехбитовых ошибок. Кроме того, декодер можно сконструировать так, чтобы он исправлял некоторые комбинации с четырьмя ошибками. Поскольку исправить можно только 16,7% комбинаций с четырьмя ошибками, декодер, для упрощения, обычно реализуется для исправления только трехбитовых ошибочных комбинаций [5]. Если предположить жесткое декодирование, то вероятность битовой ошибки для расширенного кода Голея можно представить как функцию вероятности p ошибки в канальном символе (см. уравнение (6.46)).
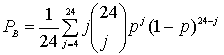 (6.77)
(6.77)
График зависимости (6.77) показан на рис. 6.21; вероятность появления ошибки для расширенного кода Голея значительно меньше, чем у кодов Хэмминга. Исходя из уравнений (6.77), (6,74) и (6.75), можно связать ![]() с
с ![]() для сигнала BPSK в гауссовом канале с кодированием расширенным кодом Голея. Результаты показаны на рис. 6.22.
для сигнала BPSK в гауссовом канале с кодированием расширенным кодом Голея. Результаты показаны на рис. 6.22.
6.8.3. Коды БХЧ
Коды Боуза-Чоудхури-Хоквенгема (Bose-Chadhuri-Hocquenghem — ВСН, БХЧ) являются результатом обобщения кодов Хэмминга, которое позволяет исправлять множественные ошибки. Они составляют мощный класс циклических кодов, который обеспечивает достаточную свободу выбора длины блока, степени кодирования, размеров алфавита и возможностей коррекции ошибок. В табл. 6.4 приводятся наиболее часто употребляемые при создании кодов БХЧ генераторы ![]() [8] с разными значениями n, k и t для блоков длиной до 255. Коэффициенты
[8] с разными значениями n, k и t для блоков длиной до 255. Коэффициенты ![]() представлены восьмеричными числами, оформленными так, что при преобразовании их в двоичные символы крайние правые разряды отвечают коэффициенту нулевой степени в
представлены восьмеричными числами, оформленными так, что при преобразовании их в двоичные символы крайние правые разряды отвечают коэффициенту нулевой степени в ![]() . С помощью табл. 6.4 можно легко проверить свойство циклического кода — полиномиальный генератор имеет порядок
. С помощью табл. 6.4 можно легко проверить свойство циклического кода — полиномиальный генератор имеет порядок ![]() . Коды БХЧ очень важны, поскольку при блоках, длина которых равна порядка несколько сотен, коды БХЧ превосходят своими качествами все другие блочные коды с той же длиной блока и степенью кодирования. В наиболее часто применяемых кодах БХЧ используется двоичный алфавит и блок кодового слова длиной
. Коды БХЧ очень важны, поскольку при блоках, длина которых равна порядка несколько сотен, коды БХЧ превосходят своими качествами все другие блочные коды с той же длиной блока и степенью кодирования. В наиболее часто применяемых кодах БХЧ используется двоичный алфавит и блок кодового слова длиной ![]() , где
, где ![]() .
.
Из названия табл. 6.4 ясно, что показаны генераторы только для примитивных кодов БХЧ. Термин "примитивные" (primitive) — это теоретико-числовое понятие, требующее алгебраического рассмотрения [7, 10-11], которое представлено в разделе 8.1.4. На рис. 6.21 и 6.22 изображены графики вероятности ошибки для двух кодов БХЧ: (127, 64) и (127, 36). На рис. 6.21 показана зависимость ![]() от вероятности ошибки в канальном символе при жестком декодировании. На рис. 6.22 показана зависимость
от вероятности ошибки в канальном символе при жестком декодировании. На рис. 6.22 показана зависимость ![]() от
от ![]() для когерентно демодулированного сигнала BPSK в гауссовом канале. Кривые на рис. 6.22 выглядят совсем не так, как можно было бы ожидать. Все они имеют одну и ту же длину блока, но большая избыточность кода (12, 36) не дает той эффективности кодирования, какая имеется у менее избыточного кода (127, 64). Известно, что относительно широкий максимум эффективности кодирования, в зависимости от степени кодирования при фиксированном n, для кодов БХЧ находится примерно между степенью 1/3 и 3/4 [12]. Стоит также отметить, что передача по гауссову каналу сильно ухудшается при переходе от очень высоких до очень низких скоростей [11].
для когерентно демодулированного сигнала BPSK в гауссовом канале. Кривые на рис. 6.22 выглядят совсем не так, как можно было бы ожидать. Все они имеют одну и ту же длину блока, но большая избыточность кода (12, 36) не дает той эффективности кодирования, какая имеется у менее избыточного кода (127, 64). Известно, что относительно широкий максимум эффективности кодирования, в зависимости от степени кодирования при фиксированном n, для кодов БХЧ находится примерно между степенью 1/3 и 3/4 [12]. Стоит также отметить, что передача по гауссову каналу сильно ухудшается при переходе от очень высоких до очень низких скоростей [11].
| k | t | g(x) n | k | t | g(x) | |
| 85 |
6 |
130704476322273 | 55 | 31 | 7315425200350110013301527530 6032054325414326755010557044 426035473617 | |
| 78 |
7 |
26230002166130115 | ||||
| 71 |
9 |
625501010703253127753 | 47 | 42 | 2533542017062646563033041377 4062330751233341454460450050 66024552543173 | |
| 64 |
10 |
1206534025570773100045 | ||||
| 57 |
11 |
335265252505705053517721 | 45 | 43 | 1520205605523416113110134637 6423701563670024470762373033 202157025051541 | |
| 50 |
13 |
54446512523314012421501421 | ||||
| 43 |
14 |
17721772213651227521220574343 | 37 | 45 | 5136330255067007414177447245 4375304207357061743234323476 4354737403044003 | |
| 36 |
15 |
3146074666522075044764574721735 | ||||
| 29 |
21 |
403114461367670603667530141176155 | 29 | 47 | 30257155366730714655270640123 61377115342242324201174114060 254757410403565037 | |
| 22 |
23 |
123376070404722522435445626637647043 | ||||
| 15 |
27 |
22057042445604554770523013762217604353 | ||||
| 8 |
31 |
7047264052751030651476224271567733130217 | 21 | 55 | 12562152570603326560017731536 07612103227341405630745425211 53121614466513473725 | |
| 255 | 247 |
1 |
435 | |||
| 239 |
2 |
267543 | ||||
| 231 |
3 |
156720665 | 13 | 59 | 4641732005052564544426573714 2500660043306774454765614031 7467721357026134460500547 | |
| 223 |
4 |
75625541375 | ||||
| 215 |
5 |
23157564726421 | ||||
| 207 |
6 |
16176560567636227 | 9 | 63 | 1572602521747246320110310432 5535513461416236721204407454 5112766115547705561677516057 | |
| 199 |
7 |
7633031270420722341 | ||||
| 191 |
8 |
2663470176115333714567 | ||||
| 187 |
9 |
52755313540001322236351 | ||||
| 179 |
10 |
22624710717340432416300455 | ||||
| 4 |
1 |
13 | 55 | 31 | 7315425200350110013301527530 6032054325414326755010557044 426035473617 | |
| 11 |
1 |
23 | ||||
| 7 |
2 |
721 | 47 | 42 | 2533542017062646563033041377 4062330751233341454460450050 66024552543173 | |
| 5 |
3 |
2467 | ||||
| 26 |
1 |
45 | 45 | 43 | 1520205605523416113110134637 6423701563670024470762373033 202157025051541 | |
| 21 |
2 |
3551 | ||||
| 16 |
3 |
107657 | 37 | 45 | 5136330255067007414177447245 4375304207357061743234323476 4354737403044003 | |
| 11 |
5 |
5423325 | ||||
| 6 |
7 |
313365047 | 29 | 47 | 30257155366730714655270640123 61377115342242324201174114060 254757410403565037 | |
| 57 |
1 |
103 | ||||
| 51 |
2 |
12471 | ||||
| 45 |
3 |
1701317 | 21 | 55 | 12562152570603326560017731536 07612103227341405630745425211 453121614466513473725 | |
| 255 | 39 |
4 |
166623567 | |||
| 36 |
5 |
1033500423 | ||||
| 30 |
6 |
157464165547 | 13 | 59 | 4641732005052564544426573714 2500660043306774454765614031 7467721357026134460500547 | |
| 24 |
7 |
17323260404441 | ||||
| 18 |
10 |
1363026512351725 | ||||
| 16 |
11 |
6331141367235453 | 9 | 63 | 1572602521747246320110310432 5535513461416236721204407454 5112766115547705561677516057 | |
| 10 |
13 |
472622305527250155 | ||||
| 7 |
8 |
5231045543503271737 | ||||
| 120 |
1 |
211 | ||||
| 113 |
2 |
41567 | ||||
| 106 |
3 |
11554743 | ||||
| 99 |
4 |
3447023271 | ||||
| 92 |
5 |
624730022327 |
На рис. 6.23 показаны расчетные характеристики кодов БХЧ для когерентно демодулированного сигнала BPSK с жестким и мягким декодированием. Мягкое декодирование для блочных кодов не применяется из-за своей сложности, хотя оно и дает увеличение эффективности кодирования порядка 2 дБ по сравнению с жестким декодированием. При данной степени кодирования вероятность ошибки при декодировании уменьшается с ростом длины блока п [4]. Таким образом, при данной степени кодирования интересно рассмотреть необходимую длину блока для сравнения характеристик жесткого и мягкого декодирования. На рис. 6.23 все коды показаны со степенью кодирования, равной приблизительно 1/2. Из рисунка [13] видно, что при фиксированной степени кодирования и жестком декодировании кода БХЧ длиной 8n или более наблюдаются лучшие характеристики, чем при мягком декодировании кода БХЧ длиной n. Существует специальный подкласс кодов БХЧ (которые были разработаны раньше кодов БХЧ), который является недвоичным набором; это коды Рида-Соломона (Reed-Solomon code). Подробнее об этих кодах будет рассказано в разделе 8.1.
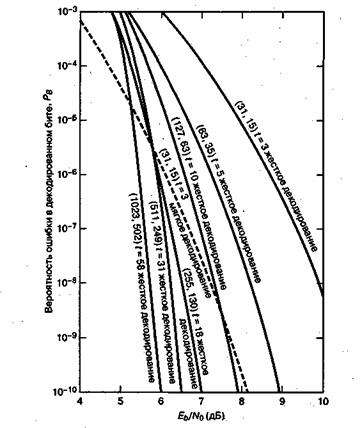
Рис. 6.23. Зависимость ![]() от
от ![]() для когерентно демодулируемого сигнала BPSK в гауссовом канале с использованием кодов БХЧ.
для когерентно демодулируемого сигнала BPSK в гауссовом канале с использованием кодов БХЧ.

