Реальные процессы описываются действительными функциями времени. Однако при рассмотрении многих задач удобно выражать сигнал в виде суммы элементарных сигналов, каждый из которых является комплексной функцией времени, либо рассматривать сам сигнал как комплексную функцию

(2.98)

где U(t) и ψ(t) — огибающая и фаза сигнала. Действительный сигнал s(t) в этом случае определяется следующим выражением:

(2.99)

Такое представление особенно удобно для узкополосных сигналов.

Сигнал называется «аналитическим», если s(t) и составляют пару преобразований Гильберта:

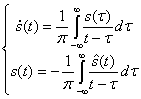(2.100)

Интегралы в этих соотношениях понимаются в виде главного значения Коши. Функция называется сопряженной с функцией по Гильберту. При таком выборе s(t) и огибающая и фаза сигнала определяются однозначно:

(2.101)

(2.102)

Если эффективная ширина спектра сигнала s(t) мала по сравнению с его средней частотой , то U(t) и ψ(t) изменяются медленно по сравнению с функцией s(t). Легко показать, что функции s(t)=cosωt соответствует сопряженная функция = sinωt, а функции s(t) =sinωt соответствует =сosωt. Если исходный сигнал представлен рядом Фурье s(t) =

то сопряженная ему функция будет

Таким образом, простейшему сигналу в виде гармонического колебания s(t)=Acosωt соответствует аналитический сигнал s(t)=Аcosωе+iФsinωе=Ae^iωt Если сигнал s(t) может быть представлен в виде интеграла Фурье s(t)=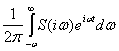, то частотный спектр сигнала будет

Спектры функций s(t) и связаны между собой следующим образом:

(2.103)

где sgn(ω)=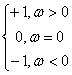

Таким образом, преобразование Гильберта сигнала s(t) можно рассматривать как результат прохождения s(t) через цепь, сдвигающую фазу всех частотных компонент спектра на угол — 90°. Частотная и переходная характеристики этой цепи таковы:

K(iω)=-isgn(ω),

h(t)=1/πt.

Подстановка выражения (2.103) в преобразование Фурье функции (2.98) показывает, что спектр S(iω) сигнала s(t) является «односторонним»:

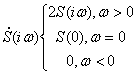(2.104)

Это очень полезное свойство аналитического сигнала.

Для периодических функций s(t) сопряженная по Гильберту

функция также является периодической с тем же периодом. Эти функции на отрезке, равном их периоду Т, взаимно ортогональны, т. е.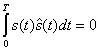

Сигналы s(f) и, для которых условие ортогональности сохраняется при замене одного из них на сопряженный по Гильберту, т. е. когда выполняются условия

(s,)= 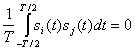(2.105)

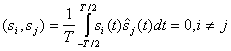
называются ортогональными в усиленном смысле. Можно показать, что такие сигналы также удовлетворяют и условию

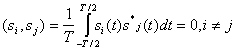(2.106)

где «звездочка» обозначает комплексно-сопряженную величину.

Введение понятия «аналитический сигнал» позволяет представить любую функцию времени (гари несущественных ограничениях) в комплексном виде и однозначно определить огибающую и фазу сигнала. В аналитической форме (2.98) могут быть представлены как детерминированные, так и случайные сигналы. Полезность такого представления состоит в возможности отдельного рассмотрения огибающей и фазы процесса (сигнала или помехи) . Так, при исследовании случайного процесса можно вместо изучения мгновенных значений ограничиться изучением огибающей и фазы процесса, а во многих случаях — либо огибающей, либо фазы.

В общем случае спектры и корреляционные функции процессов

x(t) и одинаковы: , Вх(ω) = .

Взаимный энергетический спектр равен =, а взаимная корреляционная функция, определяется выражением

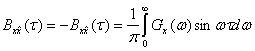. Между законом распределения случайного процесса x(t) с одной стороны и законами распределения огибающей U и фазы ψ с другой существует жесткая связь: зная закон распределения р(х), можно найти законы распределения p(U) и p(ψ). Сравнительно легко эта связь устанавливается в случае гауссовых процессов (см. § 2.3).