Условие баланса фаз в автогенераторе, как было показано выше, определяется выражением:

j_э + j_s + j_к =0 (2mπ) (2.4)

Поскольку фазовые углы j_s и j_к малы и при малых изменениях частоты меняются очень мало, то для простоты рассуждений при рассмотрении устойчивости фазы можно принять их равными нулю. Тогда условие баланса фаз примет вид:

j_э =0 . ( 2.4’)

При этом частота автоколебаний в стационарном режиме равна резонансной частоте контура.

Фаза (частота) автоколебаний будет устойчива в том случае, когда при малом случайном изменении частоты w фазовый угол j_э будет изменяться так, чтобы частота автоколебаний возвратилась к своему значению при состоянии равновесия фаз.

Можно показать, что устойчивость фазы (частоты) автогенератора обеспечивается его колебательным контуром. Математически условие устойчивости фазы (частоты) автогенератора выражается формулой:

<0 (2.10)

Это можно пояснить следующим образом. При изменении частоты, например, при w < w_раб,первая гармоника анодного тока будет отставать от напряжения на контуре (рис.2.5). Однако, из рис.2.5 видно, что напряжение обратной связи , синфазное с напряжением на контуре , опережает напряжение, поэтому фазовый сдвиг между и будет уменьшаться.

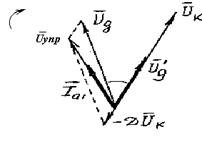
Рис 2.5.

Итак, устойчивость амплитуды колебаний в автогенераторе определяется лампой (нелинейным характером её внутреннего сопротивления и зависимостью его величины от электронного режима лампы), а устойчивость их частоты (фазы) - колебательным контуром.