Полученная в результате аппроксимации функция цепи F(x) подлежит в дальнейшем реализации в виде конкретной схемы. Существует большое число методов реализации цепи по функции квадрата АЧХ |H(j)|², ФЧХ () или характеристике ГВП t_гр(), по переходной g(t) и импульсной h(t) характеристикам.

Существуют общие методы синтеза операторных передаточных функций. Остановимся лишь на методах, имеющих в настоящее время практическое значение: 1) синтез скрещенных (мостовых) схем с постоянным входным сопротивлением; 2) синтез симметричных Т-перекрытых схем с постоянным характеристическим сопротивлением; 3) синтез реактивных лестничных четырехполюсников, нагруженных резистивным сопротивлением; 4) синтез ARС-цепей.

Нахождение операторной передаточной функции по квадрату модуля комплексной передаточной функции. Предположим, что в результате решения задачи аппроксимации найден квадрат модуля комплексной передаточной функции (квадрат АЧХ). Далее необходимо знать операторную передаточную функцию. Определение квадрата модуля комплексной передаточной функции по соответствующей операторной функции осуществляется при помощи замены переменной р на j, и решается однозначно, т. е. операторной передаточной функции соответствует только один квадрат модуля комплексной передаточной функции.

Обратная задача решается несколько сложнее и неоднозначно. Вначале сформулируем теорему о квадрате модуля передаточной функции.

Теорема. Квадрат модуля комплексной передаточной функции не изменится, если изменить знак у всех или у некоторой части нулей и полюсов соответствующей операторной передаточной функции, а также если у комплексных нулей и полюсов знак изменяется одновременно у каждой комплексно сопряженной пары.

Докажем утверждение, что если в формуле для квадрата модуля выполнить обратную подстановку = —jp, то полученная функция обладает следующими свойствами: 1) функция |H(р)|² содержит в 2 раза больше нулей и полюсов, чем функция Н(р); 2) если функция Н(р) имеет нуль, равный р_0i, то |H(р)|², кроме р_0i, имеет нуль – р_0i. Это означает, что при наличии нуля Н(р) в левой полуплоскости, в |H(р)|² появляется дополнительный нуль в правой полуплоскости и наоборот. Сказанное полностью относится к полюсам. Действительно, квадрат модуля передаточной функции представим в виде (16.20)

Выполним замену j = p или = —jp. Из формулы (16.7) видно, что

Пусть функция Н(р) имеет n нулей и m полюсов, тогда ее можно представить в виде (7.42): 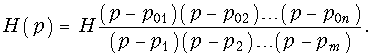т. е. Н(—р) содержит все нули и полюсы, что и Н(р), но с противоположными знаками. Это и требовалось доказать.

Проведенный анализ позволяет сформулировать порядок определения операторной передаточной функции по квадрату ее модуля: 1. В выражении для |H(j)|² выполняем замену = —jр. 2. Находим все нули и полюсы функции |H(p)|², половина из которых принадлежит функции Н(р). Полюсы, лежащие в левой полуплоскости относим к Н(р). Они составляют как раз половину всех полюсов. Остальные полюсы относятся к Н(—р). Такое распределение полюсов вызвано необходимостью получения устойчивых цепей. Таким образом, выбор полюсов передаточной функции осуществляется однозначно. 3. Распределение нулей функции |H(p)|² между Н(р) и Н(–р) не может быть выполнено однозначно. Согласно теореме о квадрате модуля передаточной функции здесь имеется определенная свобода в выборе числителя передаточной функции. Если на ФЧХ никаких ограничений не накладывается, то обычно и нули выбирают в левой полуплоскости. 4. Постоянный множитель функции Н(р) равен квадратному корню из постоянного множителя функции |H(p)|² .

Пример. Определить операторную передаточную функцию, если квадрат ее модуля имеет вид

1. Записываем |H(p)|² путем замены = —jp в выражении для |H(j)|²

2. Находим нули и полюсы |H(p)|²:

Функция H(p): будет иметь полюсы р₆ и р₈, так как они находятся в левой полуплоскости.

3. Что касается нулей, то возможны следующие сочетания:

4. Постоянный множитель H = 5/2.

Запишем передаточную функцию для второго возможного сочетания нулей

Рассмотрим перечисленные выше методы синтеза передаточных функций.

Синтез скрещенных (мостовых) схем с постоянным входным сопротивлением. Этот метод является общим, т. е. любую операторную функцию, удовлетворяющую УФР, можно с точностью до постоянного множителя реализовать мостовой схемой с постоянным входным сопротивлением. Метод имеет важное теоретическое значение, так как доказывает достаточность УФР. В практическом плане этот метод применяется при синтезе фазовых корректоров и линий задержки. Мостовая схема четырехполюсника, нагруженная с обеих сторон на сопротивление R₀ показана на рис. 16.12.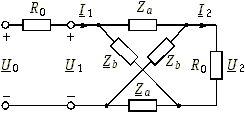

Если двухполюсники Z_a и Z_b являются обратными, т. е. Z_a Z_b = R₀², то передаточная функция имеет вид 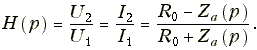(16.21a)

Пусть задана передаточная функция H(p), удовлетворяющая УФР. Тогда для ее реализации мостовой схемой необходимо синтезировать двухполюсники с входными функциями: 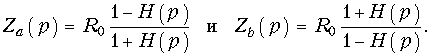(16.21 б, в)

Синтез таких двухполюсников возможен, если доказать, что функции (16.21 б, в) являются ПВФ (на самом деле достаточно доказать, что ПВФ является Z_a, тогда функция сопротивления обратного двухполюсника также является ПВФ). Чтобы это доказать, вспомним, что ПВФ – это дробно-рациональная функция, вещественная часть которой неотрицательная в правой полуплоскости. То что Z_a является дробно-рациональной, вытекает из того, что Н(р) – дробно-рациональная функция. Для определения условий, при которых , представим операторную передаточную функцию в виде суммы вещественной и мнимой частей:

Тогда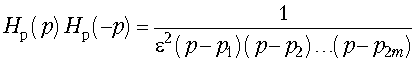

Вещественная часть Z_a будет неотрицательной, если x² + y² = |H(p)|² 1. Данное неравенство и является условием того, что Z_a(p) – ПВФ, а значит и условием физической реализуемости операторных передаточных функций в виде мостовой схемы с постоянным входным сопротивлением. Так как Н(р) удовлетворяет УФР, то она аналитическая (отсутствуют полюсы) в правой полуплоскости комплексной переменной р, а значит и ограничена по модулю |H(p)| М. Выбрав постоянный множитель Н = 1/M, получим функцию, реализуемую с точностью до постоянного множителя в виде мостовой схемы. Таким образом, реализация передаточной функции сводится к синтезу двухполюсников Z_a и Z_b. Отметим, что на практике заданную передаточную функцию реализуют не в виде одной сложной мостовой схемы, а в виде каскадного соединения более простых мостовых схем. Для этого заданную функцию представляют в виде произведения более простых функций:

Каждая функция реализуется в виде мостовой схемы. Если сопротивление выбрано для всех схем одинаковым, то получается каскадное соединение согласованных четырехполюсников, и переданная функция каскадного соединения как раз и является произведением передаточных функций четырехполюсников, составляющих это каскадное соединение.

Синтез симметричных Т-перекрытых схем с постоянным характеристическим сопротивлением. Для симметричного Т-перекрытого четырехполюсника, показанного на рис. 16.13, а, характеристические сопротивления

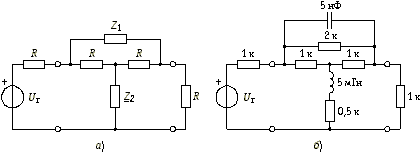
Рис. 16.13

при взаимно-обратных двухполюсниках Z₁Z₂ = R² равны R, т. е. четырехполюсник включен согласованно. Следовательно, его собственная постоянная передачи непосредственно связана с рабочей передаточной функцией или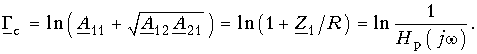

Отсюда

Из последнего равенства и условия Z₁(р)Z₂(р) = R² находим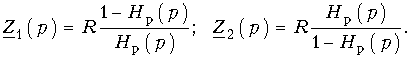

Двухполюсники Z₁(p) и Z₂(p) в плечах схемы рис. 16.13, а могут быть реализованы известными способами.

Пример. В результате аппроксимации получена функция |H_р(j )|² = ( ² + 10¹⁰)/(² + 9×10¹⁰). Осуществим ее реализацию в виде симметричного Т-перекрытого четырехполюсника (см. рис. 16.13, а) при нагрузке на сопротивление R = 1 кОм.

Заменим оператор j на р: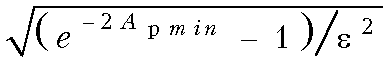

Очевидно, что H_р(p) = (p + 10⁵)/(p + 3×10⁵). Сопротивление Z₁(p) в схеме на рис. 16.13, а определяется по формуле: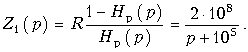

Разложение Z₁(p) в цепную дробь: приводит к схеме параллельного RС-контура с элементами С = 5 нФ и R₁ = 2 кОм.

Двухполюсник Z₂(p) является обратным, т. е. последовательным RL-контуром с элементами L = 5 мГн и R₂ = 0,5 кОм.

Схема реализованного четырехполюсника приведена на рис. 16.13, б.

Синтез реактивных лестничных четырехполюсников, нагруженных резистивными сопротивлениями (рис. 16.14) основан на том очевидном факте, что активная мощность, отдаваемая генератором , равна мощности, потребляемой нагрузкой , т. е.

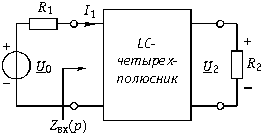
Рис. 16.14

Ток I₁ выразим через задающее напряжение генератора U₀ и подставим в предыдущее равенство. После алгебраических преобразований, получим: 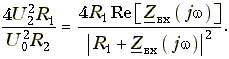(16.22)

Левая часть данного уравнения представляет собой квадрат модуля рабочей передаточной функции (12.44), а числитель правой части можно представить следующим образом: (16.23)

Убедиться в справедливости уравнения (16.23) можно путем элементарных преобразований его правой части. С учетом сказанного уравнения (16,23) преобразуется к виду: 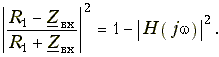(16.24)

Из последней формулы можно найти операторное входное сопротивление Z_вx(p). Реализуя Z_вx(p) в виде лестничной структуры, получаем цепь с заданной передаточной функцией Н(р). При этом, конечно, нужно следить, чтобы реализовывались нули передаточной функции.

Обозначая 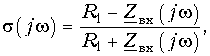(16.25) где – коэффициент отражения мощности на входе четырехполюсника, получим из (16.24) связь между квадратом частотной характеристики коэффициента отражения и квадратом АЧХ четырехполюсника: (16.26)

Практические аспекты применения данного метода будут рассмотрены при синтезе фильтров.

Синтез ARС-цепей. Активные RС-цепи возникли как альтернатива RLC-цепям. Дело в том, что катушки индуктивности, а значит и в целом RLC-цепи плохо поддаются микроминиатюризации и обладают значительной массой и габаритами. Активные RС-цепи в принципе допускают микроминиатюризацию, что является их явным достоинством. Существенным же недостатком ARС-цепей является их относительно низкая стабильность, относительно высокий уровень собственных шумов и нелинейных искажений. Поэтому ARС-цепи применяются в основном в области низких частот приблизительно до 100 кГц. На более высоких частотах применяются ARС-цепи невысоких порядков. Ниже кратко описаны методы синтеза ARС-цепей, которые нашли применение на практике.

Имитация в RLC-цепях индуктивностей их электронными эквивалентами. Существуют активные многополюсники, называемые обобщенными преобразователями сопротивлений, которые, будучи нагруженными на емкости или резисторы, реализуют на своих входных зажимах некоторую цепь, состоящую из индуктивностей. В простейшем случае индуктивность можно реализовать нагруженным на емкость гиратором. Данный метод синтеза ARС-цепи сводится к синтезу пассивной RLC-цепи с последующей заменой всех индуктивностей их электронными эквивалентами.

Синтез ARC-цепей по моделям. Этот метод заключается в том, что рассматривается ARС-схема, состоящая из одного или нескольких активных элементов и некоторого RС-многополюсника. Методами анализа электрических цепей находится операторная передаточная функция, выраженная через параметры RС-многополюсника и активного элемента. Сравнивая заданную передаточную функцию с полученной, определяют параметры синтезируемой схемы (метод выравнивания коэффициентов). Чаще всего в качестве активного элемента выбирают ОУ с бесконечным коэффициентом усиления и задаются структурой многополюсника.

Анализ цепей с ОУ основывается на замене ОУ зависимым источником. Согласно этому методу сформулируем алгоритм нахождения операторных передаточных функций цепей с ОУ. Он состоит из следующих шагов: 1. Ко входу цепи подключить какой-либо источник. 2. Заменить все ОУ их схемами замещения (зависимыми источниками) с конечным коэффициентом усиления Н_у. 3. Любым методом анализа цепей определить изображение по Лапласу входных (U₁(p) или I₁(p)) и выходных (U₂(p) или I₂(p)) напряжений и токов. 4. Взять отношение найденных изображений и в этом отношении сделать предельный переход при Н_у .

Пример. Зададимся моделью, показанной на рис. 16.15.

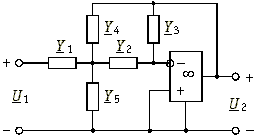
Рис. 16.15

При коэффициенте усиления ОУ, стремящемся к бесконечности, операторная передаточная функция примет вид:

Пусть Y₁ = G₁, Y₂ = G₂, Y₄ = G₄, Y₅ = pC₅, Y₃ = pC₃, тогда (16.27)

Таким образом, данной схемой можно реализовать передаточную функцию вида (16.28)

Из сравнения выражений (16.27) и (16.28) следует, что

Полученная система из трех уравнений содержит шесть неизвестных. Она имеет множество решений. Наложим дополнительные ограничения на неизвестные. Пусть G₁ = G₂ = G₃ = G₄ = G, тогда система уравнений преобразуется к виду

Отсюда следует, что C₅ = 3G/a, C₃ = a/3, Н = . Задавшись конкретным значением G, найдем C₃ и C₅.

Если проводимостям исходной схемы приписать другие значения, то можно реализовать множество различных функций.

Каскадная реализация заключается в представлении заданной передаточной функции в виде произведения множителей обычно второго, а иногда первого порядков. Такие функции в силу их простоты несложно реализовать в виде активной схемы, которую называют звеном. Затем полученные четырехполюсники включают каскадно, причем так, чтобы взаимное влияние звеньев было пренебрежимо мало. Это достигается двумя способами: либо включением между звеньями специальных буферных (развязывающих) активных четырехполюсников (например, повторителей напряжений), или таким выбором звеньев, при котором отношение выходного и входного сопротивлений звеньев в месте соединения стремилось либо к нулю, либо к бесконечности. Другими словами, данные сопротивления должны резко отличаться друг от друга. Например, если выходное сопротивление предыдущего звена стремится к нулю, то входное сопротивление последующего звена должно стремиться к бесконечности и наоборот.