4.1. Общие положения

4.2. Энергетические соотношения для электромагнитного поля

4.3. Режимы передачи по направляющим системам

4.4. Классы и типы волн в НСС

4.5. Электромагнитные процессы в проводниках и диэлектриках

4.6. Уравнение однородной линии

4.1. Общие положения

Строгое решение задачи распространения электромагнитной энергии по направляющим системам, образующим разнообразные кабели связи требует применения средств электродинамики и решения уравнений Максвелла. Методы электродинамики позволяют решить все задачи передачи, излучения, поглощения в любой направляющей системе и в любом частотном диапазоне. НС имеет достаточно сложную структуру, поэтому их при анализе вводится ряд допущений и процесс распространения энергии разбивается на независимые процессы:

• передачу;
• излучение;
• поглощение.

Каждый из этих процессов определяет те или иные свойства НС. При анализе НС параметры среды усредняются по объему, среда обладает следующими свойствами:

• изотропностью, т.е
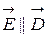
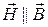
• линейностью, т.е. ;
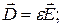
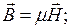
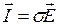• однородностью, т.е. параметры среды не зависят от координаты.

При анализе НС анализируются гармонические колебания, т.к. сигнал любой формы может быть представлен суперпозицией гармонических составляющих в виде ряда Фурье.

Уравнения Максвелла (первое и второе) обобщают основные законы электродинамики: закон полного тока и электромагнитной индукции. Уравнения записываются в интегральной (4.1) и дифференциальной форме (4.2).

; (4.1) 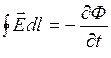; ; 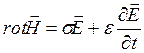(4.2) 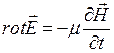. Для гармонических колебаний справедливо 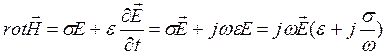(4.3)

Обозначим 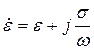, где - комплексная диэлектрическая проницаемость, соотношение мнимой и действительной частей которой определяет свойства среды:

- проводник;

- диэлектрик.

Кроме уравнений (4.1) и (4.2) используются уравнения (4.3) и (4.4).

; (4.4)

Уравнения (4.4) означают, что электрическое поле имеет заряды, а магнитные заряды не существуют. Силовые линии электрического поля начинаются и заканчиваются на зарядах, от зарядов они расходятся (или сходятся) в окружающее пространство. Силовые линии магнитного поля всегда направлены по нормали к металлическим поверхностям, линии магнитного поля параллельны к проводящим поверхностям. В соответствии с (4.2) изменяющееся во времени магнитное поле порождает переменное электрическое поле и наоборот. Процесс распространения электромагнитного поля поясняется на рисунке 4.1.

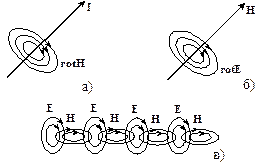
Рисунок 4.1. Распространение электромагнитного поля

4.2. Энергетические соотношения для электромагнитного поля

Рассмотрим баланс энергии электромагнитного поля. Запас энергии в объеме определяется суммой электрической и магнитной энергии:

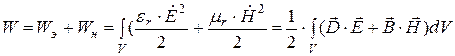(4.5)

где первое слагаемое – энергия электрического поля, а второе – магнитного. Это выражение аналогично известной формуле для колебательного контура:

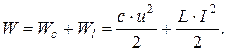
Используя выражение Максвелла можно получить выражение:

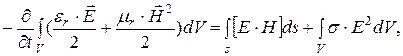(4.6)

где ds – элемент поверхности, ограничивающий объем V.

Это выражение известно как теорема Умова-Пойтинга. Левая часть выражения характеризует расход электромагнитной энергии в единицу времени. Первое слагаемое правой части представляет поток энергии в единицу времени через замкнутую поверхность S объема V в окружающее пространство. Энергия, распространяющаяся в единицу времени через поверхность, перпендикулярную направлению потока энергии, определяется величиной называется вектором Пойнтинга. Второе слогаемое определяет энергию внутри объема, которая преобразовалась в тепло.

Изменение запаса энергии, находящейся в некотором объеме V, происходит за счет расхода энергии внутри объема и распространения ее за пределы этого объема. Теорема Умова-Пойнтинга устанавливает связь между напряженностями полей Е и Н на поверхности какого-либо объема с потоком энергии, входящей в объем или выходящей из него. Зная величины Е и Н на поверхности НС можно определить поглощаемую и распространяющуюся электромагнитную энергию.

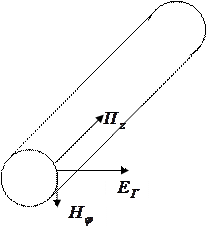
Рассмотрим одиночный проводник в полярной системе координат. Составляющие электромагнитного поля на его поверхности формируют вектор Пойнтинга, который можно разложить на составляющие, определяющие распространение энергии вдоль линии и в направлении перпендикулярном к проводнику (излучение, тепловые потери).

а) б) в)

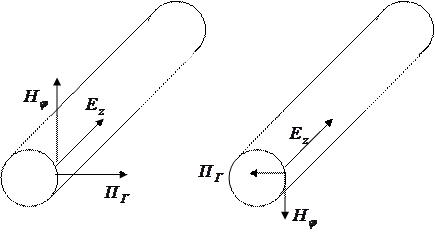
Рис. 4.2 – Составляющие вектора Пойнтинга: а) распространение, б) излучение, в) поглощение.

Продольная составляющая П_r определяет распространение энергии вдоль линии. Радиальная составляющая определяет излучение энергии в свободное пространство, в СК и КК она обуславливает взаимные влияния. Эта же составляющая, направленная внутрь проводника определяет тепловые потери.

Приведенный анализ позволяет сделать важный вывод: в НС энергия распространяется в пространстве ограниченном проводниками, проводники только направляют энергию в нужном направлении. Если к проводникам линии подключить генератор, то между проводниками возникнет переменное электромагнитное поле. Это поле, окружая проводники, движется вдоль них со скоростью, близкой к скорости света. Одновременно по линии протекает ток. Напряженность электрического поля Е соответствует напряжению U, а напряженность магнитного поля – току І.

Рис. 4.3 – Токи протекающие (I_пр) и токи смещения (I_см): а) в кабеле; б) в конденцаторе; в) в атмосфере; г) в волноводе.

Непрерывность тока, протекающего по линии обеспечиваются протеканием тока проводимости в проводниках и тока смещения в диэлектрике (как это происходит в конденсаторе). В различных НС и в различных частных диапазонах преобладают или токи смещение или токи проводимости.

Вопросы и задания для самоконтроля

1. Какие процессы возникают при распространении электромагнитной энергии?

2. Какие допущения принимаются при анализе НС?

3. Объясните смысл первого и второго уравнений Максвелла.

4. Объясните смысл третьего и четвертого уравнений Максвелла.

5. Что такое ток смещения? Приведите примеры возникновения тока смещения.

6. Объясните процесс распространения электромагнитной энергии.

7. Объясните смысл уравнения 4.4.

8. Объясните смысл уравнения 4.5.

9. Дайте определение вектора Пойтинга, объясните физический смысл его составляющих.

10. Какое назначение проводников в направляющей системе?

Письменные задания

1. Определить, при какой частоте грунт с удельным сопротивлением r=100 Ом×м/мм² приобретет свойства проводника, e_r=2,5.

2. Определить, при какой частоте медный проводник с удельным сопротивлением r=0,0175 Ом•мм²/м приобретет свойства диэлектрика.

3. Получить выражения для радиальной и продольной составляющих вектора Пойнтинга.

4. Доказать, что тангенциальной составляющей вектора Пойнтинга не существует.

5. Цепь содержит источник и последовательную RC -цепь. Обозначьте на схеме такой цепи токи проводимости и токи смещения.

6. Изобразите процесс распространения электромагнитного поля в свободном пространстве, укажите место тока смещения.

7. Укажите путь токов проводимости и смещения в волноводе.

8. Какие составляющие вектора Пойнтинга преобладают в кабеле, в антенне?

9. Объясните, какой ток (проводимости или смещения) преобладает в проводной НС, в волноводе.

10. Какой ток (проводимости или смещения) существует в ВС?

4.3. Режимы передачи по направляющим системам

В зависимости от используемых длин волн и среды распространения электромагнитной энергии выделяется пять различных режимов передачи.

Статический режим относится к процессам электростатики и магнитостатики, характеризуется отсутствием временной зависимости поля. Уравнения Максвелла имеют вид:

На основе уравнений электростатики определяется емкость проводников по формуле :

С=Q/U.

Стационарный режим относится к случаю передачи по проводникам постоянного тока І=s×Е, который создает магнитное поле, электрическое поле при этом не индукцируется и уравнения Максвелла имеют вид:

Магнитное поле имеет вихревой характер, а электрическое – безвихревой (потенциальный). В этом режиме определяется индуктивность цепи L=Ф/І, где Ф - магнитный поток, пронизывающий цепь. Для анализа процессов применяются законы Ома, Кирхгофа.

Квазистационарный режим охватывает диапазон до 10¹⁰ Гц, в этом режиме индуцируется вихревое электрическое поле, вызванное изменением электрического поля. Уравнения Максвелла имеют вид:

В этом режиме l>>D, где D – обобщенный поперечный размер НС, l - длина волны, токи смещения еще незначительны. Для анализа процесов используются законы Ома, Кирхгофа, телеграфное уравнение, волновое уравнение.

Электродинамический режим относится к области высоких частот и коротких волн (l £ D, F » 10¹⁰¸10¹² Гц). При анализе решают волновые уравнения. Уравнения Максвелла имеют вид:

Т.е. в этом режиме токами смещения пренебрегать нельзя.

Волновой и квазиоптический режимы характерны для процессов в диэлектрике, когда доминирующими являются токи смещения, а токи проводимости незначительны. В этом случае , , и Гц. При анализе процессов используются законы оптики (Гюйгенса, Френеля) и решаются волновые уравнения.

Приведенная классификация режимов характеризует универсальность уравнений Максвелла, единство законов электродинамики.

4.4. Классы и типы волн в НСС

Характер распространения электромагнитных волн в НС определяется структурой поля в ней. Эта структура определяет возможность того или иного спектра частот, что и обуславливает свойства направляющей системы. Распространяющиеся в НС волны делятся на классы и типы. Класс волны определяет наличие продольных составляющих поля ( и ). В общем случае структура поля имеет по три составляющих электрического и магнитного полей. В конкретных системах некоторые из этих составляющих обращаются в нуль. Существуют следующие классы волн:

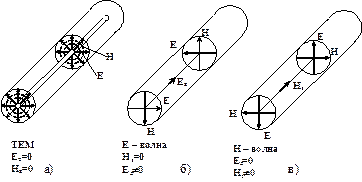
Т – поперечно-электромагнитная ТЕМ-волна ( );

Е – электрическая или поперечно-магнитная ТМ-волна ( );

Н – магнитная или поперечно-электрическая ТЕ-волна ( );

ЕН и НЕ – смешанные гибридные волны ( ).

Рис. 4.4 – Типы волн в направляющих системах

ТЕМ-волны содержат толко поперечные составляющие поля, т.е. силовые линии поля целиком лежат в поперечных плоскостях и в точности повторяют картину силовых линий статического и стационарного режимов. Эта волна существует лишь в линиях, содержащих два изолированных проводника, находящихся под разными потенциалами. Эта волна является основной в проводных НС, характеризуется токами проводимости и практически нулевыми токами смещения.

Волны Е и Н кроме поперечных составляющих содержат по одной продольной составляющей поля. Силовые линии этих волн располагаются как в поперечном, так и в продольном сечениях НС. Эти волны возбуждаются в однопроводных линиях (волноводах). По поперечному сечению НС должно уложиться целое число полуволн (не менее одной).

Гибридные волны содержат шесть компонент поля, в том числе и продольные составляющие и . Такие волны возбуждаются в световодах и диэлектрических волноводах.

Классы волн делятся также по типам. Модам тип волны или мода определяется сложностью структуры поля в поперечном сечении НС, т.е. числом максимумов и минимумов поля в этом сечении.

Мода – это самосогласованное распределение поля, которое сохраняется при распространении волны вдоль НС, не содержащей неоднородностей. Число распространяющихся мод в НС бесконечно, эти волны отличаются наличием тех или иных составляющих поля, а, следовательно, и его структурой. Различают основной тип волны и волны высших типов. Основная мода имеет простейшую структуру. В двухпроводных НС основной является ТЕМ-волна. Типы волн обозначаются двумя числовыми индексами n и m, которые означают число полных изменений (вариаций) поля по поперечным координатам.

Вопросы и задания для самоконтроля

1. Назовите режимы передачи по НС.

2. Охарактеризуйте каждый режим передачи.

3. В каком режиме передачи используются симметричный кабель, коаксиальный кабель, световод?

4. Чем определяется наличие тока смещения в НС?

5. Дайте определение класса волны.

6. Охарактеризуйте классы электромагнитных волн.

7. Дайте определение типа волны (моды).

8. Дайте определение основного типа волны.

9. Чем определяется длина волны основной моды в волноводе?

10. Какие классы волн распространяются в волноводах и световодах?

Письменные задания

1. Заполните приведенную ниже таблицу

Режим передачи	Левая часть уравнения Максвелла	Правая часть			Частота, Гц; соот-ношение D и l	Тип волны	НС для режима
		Металл	Диэлектрик
Статичес-кий
Стационар-ный
Квазиста-ционарный
Электроди-намический
Волновой и квази-оптический

2. Изобразите структуру ТЕМ-волны в:

X

Y

а) свободное пространство; б) проводящие плоскости.

3. Изобразите преобразование 2-х проводящих плоскостей и линии поля для следующих структур:

а) преобразование в б) преобразование в

коаксиальную цепь; симметричную цепь.

4. Прямоугольный волновод имеет размеры 2´4 см. Могут ли в нем распространяться гармонические колебания с частотой 10 МГц?

5. Определить типы НС, если:

a)

б)

в)

г)

6. Волновод имеет поперечные размеры 1´3 см. По волноводу распространяются моды с l=1,5 см; l=3 см; l=1 см; l=0,5 см. Какие из этих мод являются модами высшего порядка?

4.5. Электромагнитные процессы в проводниках и диэлектриках

Физические среды отличаются своими электромагнитными свойствами. Металлы и диэлектрики существенно отличаются проводимостью. Для упрощения анализа НСС часто используется понятие идеального проводника ( ) и идеального диэлектрика ( ). В идеальном проводнике существует только ток проводимости , а в идеальном диэлектрике – только ток смещения .

Металлы практически во всех диапазоне частот являются проводниками, в диэлектриках (полиэтилен, полистирол и др.) на всех частотах преобладают токи смещения. Естественные среды (почва, вода, лёд) обнаруживают свойства проводников в области низких частот, а в области высоких частот действуют как диэлектрики. Потери электромагнитной энергии в при распространении в диэлектриках незначительные. Скорость распространения электромагнитной энергии в диэлектрике определяется , где км/с – скорость света в свободном пространстве. При распространении плоской волны в диэлектрике и взаимно перпендикулярны, а отношение Е к Н определяет сопротивление среды распространяющейся волне, т.е. волновое сопротивление . Волновое сопротивление свободного пространства Ом, а волновое сопротивление диэлектриков определяется

Если по проводнику протекает переменный ток, то в нем возникает поверхностный эффект (скин-эффект), сущность которого ясна из рисунка 4.5.

Рис. 4.5 – Явление поверхностного эффекта: а) линия тока, магнитного поля и вихревых токов; б) деление токов; в) вытеснение тока на край проводника

Вследствие поверхностного эффекта ток с ростом частоты вытесняется на края проводника, т.е. протекает только по поверхности проводника, что приводит к увеличению его сопротивления при увеличении частоты. Переменный ток распространяется по сечению проводника неравномерно и затухает пропорционально , - коэффициент затухания в металле. Поверхностный эффект характеризуется эквивалентной глубиной проникновения. Эквивалентная глубина проникновения Q - это такая глубина проникновения поля в проводник, при которой напряженность поля (или плотность тока) уменьшается в =2,718 раз.

,

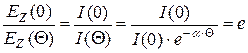тогда 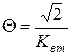, - коэффициент вихревых токов.

При увеличении частоты глубина проникновения уменьшается, т.е. поверхностный эффект с ростом частоты возрастает. Поверхностный эффект в большей степени проявляется в проводниках с большим удельным сопротивлением.

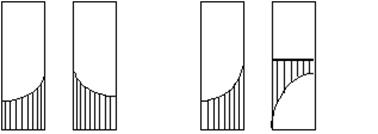
С поверхностным эффектом связаны эффект близости и эффект действия окружающих масс. Эффект близости проявляется в симметричной паре (рис. 4.6). В этом случае происходит перераспределение плотности токов в проводниках.

Рис. - 4.6 – Эффект близости в симметричной паре.

В кабеле всегда располагается несколько симметричных пар, есть другие металлические элементы. В этом случае возникает перераспределение электромагнитных полей, приводящее к изменению распределения плотности токов, что также увеличивает сопротивление цепи.

Контрольные вопросы

1. Объясните сущность поверхностного эффекта.

2. Объясните зависимость сопротивления проводника от частоты.

3. Что такое глубина проникновения?

Письменные задания

1. Запишите выражение для сопротивления проводников воздушной линии связи и витой пары.

2. Как отличается глубина проникновения в стальном проводнике по сравнению с медным ?

4.6. Уравнение однородной линии

Качество передачи по линейным цепям и их электрические свойства полностью определяются параметрами этих цепей - параметрами передачи, которые делятся на две группы - первичные и вторичные. По физической природе параметры цепей, образованных НС аналогичны параметрам колебательных контуров, составленных из элементов . В контурах эти параметры являются сосредоточенными, а в цепях связи они равномерно распределены по всей длине линии. Эти параметры являются погонными, т. е. определяются на длину линии в 1 км. Сопротивление R и индуктивность L являются продольными параметрами, они включены последовательно. Ёмкость C и проводимость изоляции G – поперечные параметры, они включены параллельно. Следует отметить, что индуктивность цепи определяется двумя составляющими – внешней и внутренней, т.е. . Внешняя индуктивность определяется только геометрией направляющей системы и не зависит от частоты, а внутренняя – поверхностным эффектом и с ростом частоты уменьшается.

Вторичные параметры передачи: затухание цепи , постоянная распространения , волновое сопротивление , постоянная фазы , скорость распространения энергии . Эти параметры полностью определяются первичными параметрами.

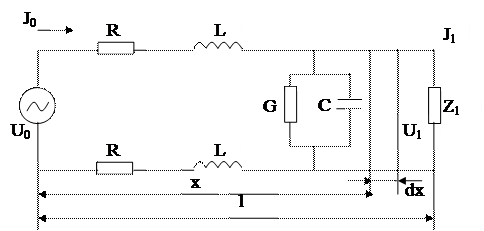
Рис. 4.6 – Схема двухпроводной цепи

На приведена эквивалентная схема двухпроводной однородной линии с первичными параметрами . В начале цепи включён генератор с выходным сопротивлением , а в конце линии нагрузка . Обозначим ток и напряжение в начале линии , в конце - .

Выделим на расстоянии х от начала линии бесконечно малый участок dx, через элемент dx протекает ток I, напряжение между проводниками на участке dx и обозначим U.

Падение напряжения на участке dx равно

. (4.7)

Утечка тока на этом участке

. (4.8)

Для решения этих уравнений исключим неизвестную величину I, продифференцировав (4.7) и, используя (4.8) :

;

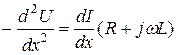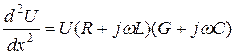, (4.9)

обозначив , получим уравнение :

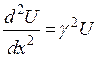. (4.10)

Решение этого уравнения имеет вид: . (4.11)

Дифференцируя (4.11) получим выражение для тока :

. (4.12)

Подставим (4.12) в (4.7), получим выражение:

. (4.13)

Введём обозначение получим систему уравнений с двумя неизвестными:

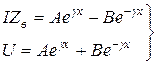. (4.14)

Для определения постоянных А и B воспользуемся значениями тока и напряжения в начале цепи (при x=0), тогда система (4.14) примет вид:

.

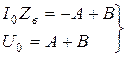Определим постоянные интегрирования

.

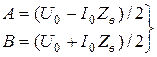Подставляя A и B в (4.14) получим

;

.

Произведя соответствующие преобразования получим значения напряжения и тока в любой точке цепи x:

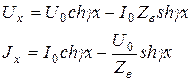(4.15)

Выражения (4.15) позволяют определить напряжение и ток в начале цепи (x=0) и в конце цепи (x=l), они устанавливают взаимную связь токов и напряжений с параметрами и . Эти уравнения справедливы при любых нагрузках и на концах цепи.

Линия называется однородной, если её первичные параметры не изменяются вдоль длины, и согласованной, если на концах она нагружена на сопротивление, равное волновому. При согласованных нагрузках и уравненя (4.15) имеют вид:

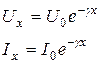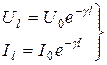; ; (4.16)

на практике, учитывая, что мощность (4.16) удобно использовать в виде:

; .

Распространение энергии по линии, ток и напряжение в любой точке цепи определяются её волновым сопротивлением и постоянной распространения.

Волновое сопротивление – это сопротивление, которое встречает электромагнитная волна при распространении вдоль однородной линии без отражения, согласованной на концах ( ). Волновое сопротивление зависит от первичных параметров цепи и частоты.

Волновое сопротивление характеризует количественное соотношение между волной напряжения U (напряженностью электрического тока E) и волной тока (напряжённостью магнитного поля H), т.е. или 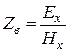. При определении волнового сопротивления рассматривается только падающая волна, т. е. отражённая волна отсутствует. Появление в линии каких-либо неоднородностей приводит к изменению структуры поля в этом сечении, изменению векторов и , а, следовательно, к изменению в этом сечении, появлению отражённых волн.

Волновое сопротивление цепи в общем случае рассчитывается по формуле

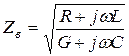. (4.17)

В однородной линии величина постоянна в любой точке цепи, и в диапазоне используемых в конкретной НС частот практически не зависит от частоты.

В общем случае является комплексной величиной и носит емкостной характер.

Коэффициент распространения является комплексной величиной и представляется в виде :

. (4.18)

Теперь 4.16 имеют вид:

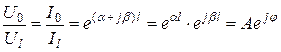. (4.19)

Модуль (4.19) определяет уменьшение абсолютного значения тока или напряжения вдоль линии. Угол характеризует изменение фазы тока или напряжения вдоль линии.

Коэффициент затухания. Электромагнитная волна, распространяясь вдоль линии уменьшается по амплитуде от генератора к нагрузке, что объясняется потерями энергии в цепи. Как следует из (4.16) мощность, амплитуда тока и напряжения уменьшаются вдоль линии по экспоненциальному закону (рис. 4.7).

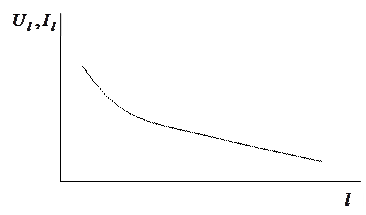
Рис. 4.6. Характер изменения мощности тока и напряжения вдоль линии

Различают два вида потерь - в проводнике и в диэлектрике. В проводнике возникают тепловые потери, в диэлектрике энергия расходуется на его поляризацию диэлектрика. Оба вида потерь возрастают с ростом частоты.

Потери в линии характеризуются коэффициентом затухания , выражение для которого можно получить из (4.18):

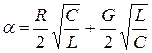. (4.20)

Действительная часть коэффициента распространения показывает уменьшение электромагнитной энергии в конце линии по сравнению с её началом

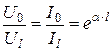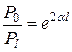; . (4.21)

Логарифмируя обе части выражений (3.15) получаем:

; .

Затухание цепи обычно представляется в децибелах (дБ) (при использовании десятичных логарифмов) или в неперах (при использовании натуральных логарифмов).

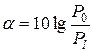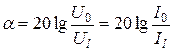; (дБ);

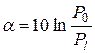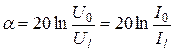; (Нп).

Между децибелами и неперами выполняется соотношение

1 Нп=8.686 дБ; 1 дБ=0.115 Нп.

Затухание является погонным параметром, измеряется на длину линии

1 км (дБ/км), с ростом частоты затухание возрастает.

Коэффициент фазы характеризует изменение фазы волны или напряжения при распространении электромагнитной волны вдоль линии, является погонным параметром, измеряется в радианах (рад/км) или градусах (град/км), определяется из (4.18):

. (4.22)

Скорость распространения энергии по цепям связи. Электромагнитная энергия распространяется по цепям связи с определенной скоростью и зависит от первичных параметров линии, определяется выражением .

Таким образом, затухание цепи определяет качество и дальность связи, а коэффициент фазы – скорость движения энергии вдоль линии.

Кроме скорости распространения энергии при анализе используются понятия фазовой и групповой скоростей. Фазовая скорость определяет скорость движения поверхности равных фаз в НС (или скорость движения волнового фронта); групповая скорость при передаче сигналов определяет скорость распространения максимума огибающей группы составляющих сложного сигнала, т.е. она характеризует скорость распространения группы волн.

Скорость распространения энергии с ростом частоты увеличивается, в области высоких частот она практически не зависит от частоты, , где С – скорость света в свободном пространстве, эта скорость всегда меньше скорости света. Для ТЕМ - волн фазовая скорость не зависит от частоты, определяется

. (4.23)

Для волн Е(ТМ) и Н(ТМ) фазовая скорость зависит от частоты и определяется

,

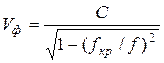где - критическая частота, при которой прекращается распространение энергии по НС.

Зависимость фазовой скорости от частоты указывает на наличие дисперсии в НС. Это обозначает, что различные типы волн в НС распространяются с различными скоростями. В двухпроводных линиях дисперсия отсутствует, дисперсия проявляется в волноводах и световодах.

Вопросы для самоконтроля

1. Объясните сущность поверхностного эффекта.

2. Объясните, какие физические процессы происходят в диэлектриках.

3. Объясните сущность эффекта близости и эффекта действия окружающих масс.

4. Что такое глубина проникновения?

5. В каких проводных НС можно пренебречь эффектом близости?

6. В каких НС нет эффекта действия окружающих масс?

7. Назовите первичные параметры передачи, объясните их смысл.

8. Назовите вторичные параметры передачи.

9. Поясните эквивалентную схему двухпроводной цепи.

10. Поясните смысл выражения 4.12.

11. Поясните смысл уравнений 4.16.

12. Дайте определение волнового сопротивления, объясните его смысл.

13. Какая линия называется однородной и согласованной?

14. Дайте определение коэффициента распространения. Поясните смысл действительной и мнимой его частей.

15. Объясните необходимость перехода к логарифмическим единицам при определении затухания.

16. Какие скорости существуют в НС, объясните их смысл.

Письменные задания

1. Приведите графики зависимостей глубины проникновения для медных и стальных проводников от частоты.

2. Как изменится глубина проникновения поля в металле при увеличении частоты в М раз?

3. Проводники имеют одинаковую проводимость и ; ; . Сравните глубину проникновения в каждом из этих проводников на частоте f.

4. Запишите выражение для полного активного сопротивления витой пары, ленточного кабеля, воздушной линии связи.

5. Приведите зависимость волнового сопротивления от частоты.

6. Из 4.18 получите аналитические выражения для затухания и коэффициента фазы.

7. Приведите характер изменения тока вдоль линии.

8. Приведите частотную зависимость скорости распространения электромагнитной энергии.

9. Приведите частотную зависимость фазовой скорости от частоты для Т- волны и для Е, Н – волны.

10. Определите километрическое затухание линии длиной 10 км., если мощность сигнала в начале линии Вт, а в конце линии мВт.

11. Определите километрическое затухание линии длиной 5 км, если дБ, а мВт.

12. При измерении волновых сопротивлений симметричной цепи на частоте 0.5 кГц, 20 кГц, 200 кГц получили следующие значения Ом, Ом, Ом. Какой частоте соответствуют измеренные волновые сопротивления?