6.1. Общая задача прохождения случайного процесса через линейные радиотехнические цепи

6.2. Определение широкополосного случайного процесса. Шумовая полоса цепи

6.3. Прохождение широкополосного случайного процесса через апериодические цепи

6.4. Прохождение широкополосного случайного процесса через частотно – избирательные цепи

6.5. Преобразование случайных сигналов нелинейными радиотехническими цепями

6.1. Общая задача прохождения случайного процесса через линейные радиотехнические цепи

В общем виде задача изучения прохождения случайных сигналов через линейные цепи состоит в определении закона распределения (функции распределения или плотности вероятности) процесса на выходе цепи при известных законе распределения входного случайного процесса и характеристик цепи. Как правило, решение задачи в общем виде наталкивается на существенные трудности. Поэтому, обычно указанную задачу сводят к определению вероятностных характеристик (математического ожидания, дисперсии, автокорреляционной функции) выходного случайного процесса. Объясняется это тем, что для практики построения и анализа радиотехнических устройств вполне достаточно знания этих характеристик.

Наиболее эффективным методом решения задачи прохождения случайного процесса через линейные цепи является спектральный метод. Напомним, что спектральный метод основывается на представлении сигнала в частотной области и знании комплексного коэффициента передачи цепи. Но если спектральный состав детерминированного сигнала определяется совокупностью комплексных амплитуд, то спектральный состав случайного сигнала определяется совокупностью значений мощности составляющих спектра, распределенных в диапазоне частот. В этом состоит особенность использования спектрального метода при анализе преобразования случайного сигнала линейной цепью.

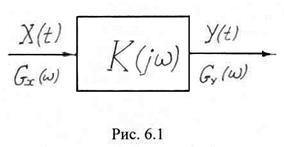Общая задача анализа прохождения случайного процесса через линейную цепь формулируется следующим образом. На вход линейной цепи (рис. 6.1) с комплексным коэффициентом передачи поступает случайный процесс , энергетический спектр которого (спектральная плотность мощности) равен . Необходимо найти характеристики случайного процесса на выходе линейной цепи.

Введем следующие предположения:

– входной случайный процесс является стационарным в широком смысле;

– среднее значение входного СП равно нулю, т.е. ;

– известен энергетический спектр входного процесса.

В соответствии с общим определением спектральной плотности мощности эта характеристика для выходного СП будет равна

. (6.1)

Величину можно представить следующим образом

, (6.2)

где – спектр реализации случайного процесса достаточно большой (теоретически бесконечной) длительности . С другой стороны, в предположении того, что реализация известна можно записать

, (6.3)

.

Подстановка (6.3) в (6.2) дает

. (6.4)

В свою очередь, подставляя (6.4) в (6.1), получим

. (6.5)

Таким образом, энергетический спектр случайного процесса на выходе линейной цепи равен произведению энергетического спектра входного случайного процесса и квадрата амплитудно–частотной характеристики цепи.

Выражение (6.5) определяет закон преобразования СП линейной цепью. Отметим, что фазо–частотная характеристика цепи не оказывает никакого влияния на этот закон.

Автокорреляционная функция выходного СП определяется в соответствии с теоремой Винера–Хинчина

. (6.6)

Так как дисперсия (средняя мощность) численно равна значению АКФ при , то для выходного СП можно записать

. (6.7)

Если входной СП имеет математическое ожидание, отличное от нуля, то математическое ожидание выходного СП определяется следующим выражением

. (6.8)

Поскольку для рассматриваемой задачи (см. предположения), то математическое ожидание .

Как было отмечено выше, в технических расчетах вместо используют энергетический спектр , как функцию циклической частоты. В этом случае энергетический спектр СП на выходе линейной цепи определяется выражением

, (6.9)

а автокорреляционная функция

. (6.10)

Соответственно, дисперсия

. (6.11)

В дальнейшем полученные результаты будут использованы для решения конкретных задач.

6.2. Определение широкополосного случайного процесса. Шумовая полоса цепи

В большинстве практических задач преобразования случайных процессов линейными цепями эффективная ширина энергетического спектра СП существенно превышает полосу пропускания цепи. Такой случайный процесс принято называть широкополосным. При этом, в пределах полосы пропускания цепи энергетический спектр приблизительно равномерен, что позволяет представить его моделью «белого шума». Вместе с тем, при определении характера входного СП (широкополосный он или нет) требуется учтение понятия ширины полосы пропускания линейной цепи.

При рассмотрении линейных инерционных цепей в качестве полосы пропускания широко используется диапазон частот, в пределах которого модуль амплитудно–частотной характеристики спадает до уровня от ее максимума. Такую полосу, как известно, принято обозначать или . Для решения задач преобразования широкополосного СП линейной цепью вводят понятие шумовой полосы цепи.

На рис. 6.2 показаны спектр входного широкополосного СП, амплитудно–частотная характеристика цепи и спектр выходного случайного процесса. Будем полагать, что входной СП – широкополосный, эффективная ширина спектра которого составляет , причем

.

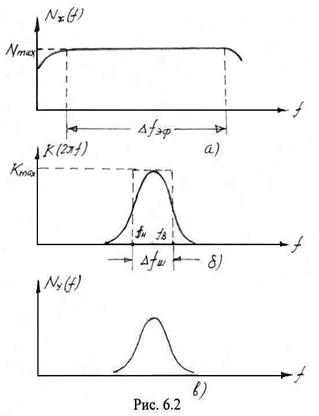Рассмотрим идеальный фильтр (для приведенного рисунка - полосовой), амплитудно – частотная характеристика которого имеет вид

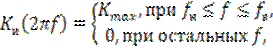6.12)где – максимальное значение АЧХ реальной цепи (рис. 6.2б).

Как следует из рисунка в пределах входной процесс можно заменить моделью «белого шума» со спектральной плотностью . При воздействии на идеальный фильтр случайного процесса со спектральной плотностью случайный процесс на выходе цепи будет иметь энергетический спектр:

.

Мощность процесса на выходе идеального фильтра

. (6.13)

С другой стороны мощность СП на выходе реальной цепи

. (6.14)

Если предъявить требование равенства мощностей на выходе идеальной и реальной цепей

, (6.15)

то полоса пропускания идеальной цепи и будет характеризовать шумовую полосу реальной цепи

. (6.16)

Тогда широкополосным случайным процессом является процесс, эффективная ширина спектра которого гораздо больше шумовой полосы цепи.

Отметим отличие от . Как следует из (6.16) зависит от всей площади под кривой и, следовательно, позволяет рассчитать полную мощность процесса на выходе цепи при равномерном спектре процесса на входе. Величина же определяется по условному критерию и не зависит от поведения АЧХ за пределами полосы пропускания.

6.3. Прохождение широкополосного случайного процесса через апериодические цепи

Рассмотрим задачу преобразования широкополосного случайного процесса вида «белого шума» со спектральной плотностью интегрирующей – цепью (рис. 6.3). Как известно, амплитудно – частотная характеристика цепи описывается выражением

,

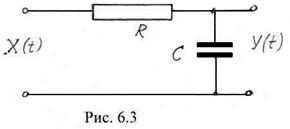
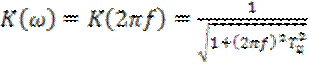где – постоянная времени цепи.

В первую очередь найдем шумовую полосу цепи. Воспользовавшись (6.16) при , получим

. (6.17)

Таким образом, шумовая полоса интегрирующей цепи конечна. Это вполне объяснимо, так как интегрирующая цепь является фильтром нижних частот.

Найдем характеристики процесса на выходе цепи, если на его вход поступает процесс с энергетическим спектром . Тогда, в соответствии с (6.9) энергетический спектр процесса на выходе цепи будет равен

. (6.18)

Автокорреляционная функция выходного процесса вычисляется в соответствии с (6.10)

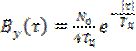. (6.19)

На рис. 6.4 изображены автокорреляционные функции и энергетические спектры входного и выходного случайных процессов. Из этих рисунков следует, что интегрирующая цепь вносит

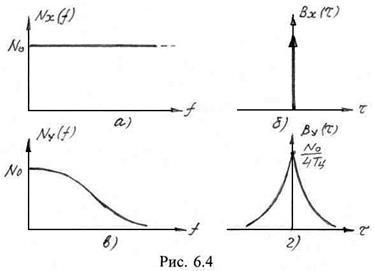корреляцию значений случайного процесса. Очевидно, дисперсия (средняя мощность) случайного процесса на выходе цепи

. (6.20)

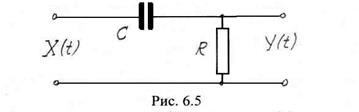Обратимся теперь к дифференцирующей – цепи (рис. 6.5).

Амплитудно – частотная характеристика цепи описывается выражением

.

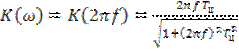При значение . Таким образом, дифференцирующая цепь является фильтром высоких частот и поэтому шумовая полоса цепи неограниченна. Действительно:

.

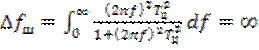Энергетический спектр СП на выходе дифференцирующей цепи:

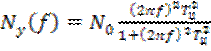. (6.21)

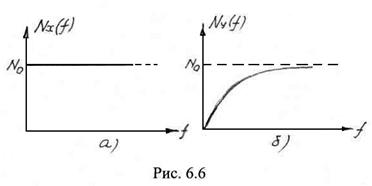На рис. 6.6 изображены энергетические спектры входного и выходного случайных процессов. Очевидно, дисперсия

.

Полученные результаты вполне объяснимы, т.к. дифференцирующая цепь по определению не относится к узкополосным цепям, т.к. для этой цепи .

6.4. Прохождение широкополосного случайного процесса через частотно – избирательные цепи

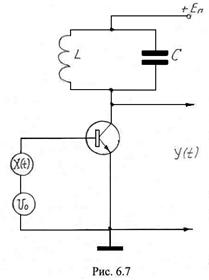Задачу преобразования широкополосного СП через частотно – избирательную цепь рассмотрим на примере одноконтурного резонансного усилителя (рис. 6.7) в режиме малого сигнала. В этом режиме, как известно, усилитель можно считать линейной частотно – избирательной цепью.

Амплитудно – частотная характеристика усилителя в режиме малого сигнала описывается выражением

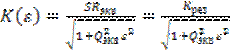, (6.22)

где , .

Переходя от относительной к абсолютной расстройке, запишем

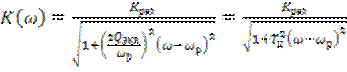, (6.23)

где – постоянная времени цепи.

Найдем шумовую полосу резонансного усилителя

,

или в циклических частотах

. (6.24)

Перейдем к рассмотрению статистических характеристик процесса на выходе резонансного усилителя, если на его вход поступает широкополосный СП вида «белого шума» с энергетическим спектром . В соответствии с (6.9) и с учетом того, что

,

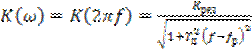получим выражение для энергетического спектра процесса на выходе усилителя

, (6.25)

Автокорреляционная функция находится в соответствии с теоремой Винера–Хинчина

. (6.26)

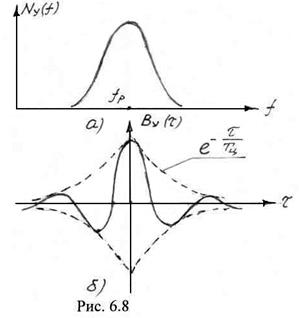
На рис. 6.8 изображены энергетический спектр и автокорреляционная функция процесса на выходе усилителя. Из рисунка следует, что АКФ выходного процесса имеет колебательный характер, уменьшаясь по закону . При этом, чем больше добротность контура, т.е. чем больше , тем медленнее спадает АКФ. Теоретически при АКФ выходного процесса преобразуется в АКФ детерминированного радиосигнала с частотой . Объясняется это тем, что при любая реализация СП на выходе представляет собой квазигармоническое колебание, частота которого в среднем равна резонансной частоте контура. И наконец, дисперсия (средняя мощность) выходного процесса

. (6.27)

6.5. Преобразование случайных сигналов нелинейными радиотехническими цепями

Решение задачи преобразования случайных сигналов линейными радиотехническими цепями осуществлялось спектральным методом. При этом, определялись характеристики , , при известных и комплексном коэффициенте передачи цепи . Что касается функции распределения или плотности вероятности значений выходного процесса, то задача их определения является достаточно сложной и поддается решению лишь в отдельных частных случаях.

При решении задачи преобразования случайного процесса нелинейными цепями, наоборот, плотность вероятности определяется сравнительно просто, а определение и сопряжено со значительными трудностями. Поэтому, постановка задачи преобразования СП нелинейными цепями отличается от постановки задачи преобразования СП линейными инерционными цепями.

Напомним, что основной характеристикой нелинейного безынерционного элемента является вольт – амперная характеристика

, (6.28)

где – входной сигнал,

– выходной сигнал нелинейного элемента.

Отметим, что входной и выходной сигналы связаны детерминированной функциональной зависимостью .

Так как в рассмотренном случае входной и выходной сигналы являются случайными процессами, т.е.

, ,

то выражение (6.28) можно записать так

. (6.29)

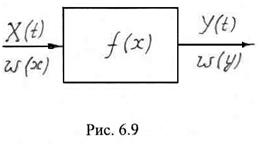
Сформулируем теперь задачу. На вход безынерционного нелинейного элемента, описываемого характеристикой (6.29) поступает стационарный случайный процесс с известной плотностью вероятности (рис. 6.9). Необходимо определить плотность распределения вероятности выходного процесса . Задачу будем решать при следующих предположениях:

– входной процесс является стационарным эргодическим процессом;

– существует и известна функция

, (6.30)

обратная функции .

Изобразим на рис. 6.10 а) зависимость и реализации входного и выходного случайных процессов.

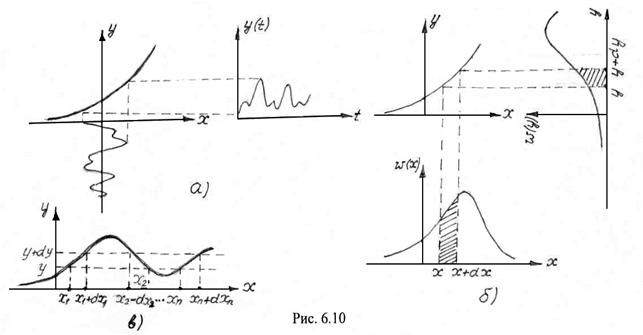
Поскольку процесс подвергается неслучайному функциональному преобразованию этому же преобразованию подвергается и плотность вероятности . На рис. 6.10б показана характеристика и кривые плотности вероятности и входного и выходного случайных процессов.

Установим соответствие между и . Выберем некоторое значение входного процесса. Этому значению однозначно соответствует значение выходного процесса. Придадим значению элементарное приращение . Этому приращению будет соответствовать элементарное приращение выходного процесса. Так как зависимость однозначна, то вероятность того, что значение случайной величину будет находиться в пределах , должна быть равна вероятности того, что случайная величина будет находится в пределах , т.е.

. (6.31)

Но, с другой стороны

,

.

Тогда (6.31) можно представить следующим образом

, (6.32)

откуда следует

. (6.33)

Производная в (6.33) вычисляется по абсолютной величине (по модулю) в силу того, что функция может быть отрицательной, а плотность вероятности всегда положительна.

Так как по условию задачи известна функция обратная , т.е. , то (6.33) можно записать так

. (6.34)

Выражение (6.34) является основным результатом решения задачи нелинейного преобразования.

Если функция неоднозначна (имеет несколько ветвей (рис. 6.10 в)), то (6.34) принимает вид

. (6.35)

Перейдем к определению вероятностных характеристик выходного процесса. Математическое ожидание при известном определяется следующим образом

.

Но с другой стороны, учитывая (6.32), а также , получим

. (6.36)

Аналогично, для дисперсии

. (6.37)

Расчеты по этой формуле достаточно просты, если допускает степенную аппроксимацию.

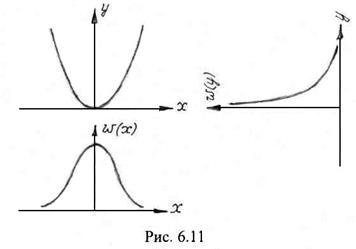
Выражение (6.34) позволяет найти при конкретном виде зависимости . Так, пусть на вход нелинейного элемента с характеристикой , поступает случайный сигнал с нормальной одномерной плотностью вероятности (рис. 6.11)

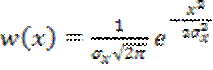. (6.38)

Найдем функцию, обратную функции

.

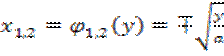Модуль первой производной

.

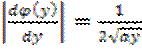Далее отметим, что функция двузначна (имеет две ветви) и сигнал при любом принимает неотрицательные значения.

С учетом отмеченных обстоятельств, воспользовавшись (6.35) запишем:

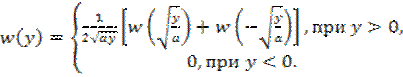
Но для нормального закона (6.38)

,

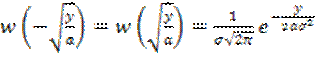Тогда окончательно получим

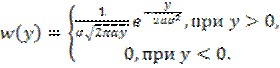
На рис. 6.11 изображена кривая плотности вероятности .