До сих пор мы рассматривали системы передачи информации, в которых параметры канала неизменны. Вероятность ошибки в таких системах обусловлена лишь наличием аддитивных помех. Оптимальный приемник использует все параметры сигнала и обеспечивает максимально возможную помехоустойчивость. В реальных условиях параметры канала и соответственно параметры сигнала могут случайно изменяться. Эффективное использование параметров сигнала на приеме в этих условиях затрудняется и помехоустойчивость неизбежно ухудшается.

В реальных каналах сигналы на вход приемника могут приходить по разным путям с различными затуханиями μк и различными запаздываниями τк. Принимаемый сигнал x(t) в этом случае можно представить в виде суммы

(5.74)

где μк и τк. — случайные процессы, вообще говоря, зависящие от времени, w(t) — аддитивная помеха. Каналы, описываемые выражением (5.74), называются многолучевыми.

Во многих случаях имеет место только один путь распространения

(5.75)

Такие каналы называются однолучевыми. Если величины μ и τ фиксированы во времени, то имеем канал с постоянными параметрами. К таким каналам можно отнести каналы проводной связи и укв каналы при передаче в пределах прямой видимости.

Почти все виды радиоканалов относятся к каналам со случайно изменяющимися параметрами. К этому классу каналов принадлежат коротковолновые линии связи, в которых благодаря изменению состояния ионосферы происходят непрерывные колебания амплитуды сигнала в точке приема. Случайные изменения условий распространения радиоволн имеют место на ультракоротких волнах, а также на средних и даже длинных волнах.

Любые изменения коэффициента передачи и времени распространения сигналов вызывают флуктуации сигналов на выходе каналов и могут рассматриваться как действие помех. Изменения коэффициента μ проявляются в виде флуктуации амплитуды сигнала и называются мультипликативной помехой. Случайные задержки лучей вызывают фазовые и временные флуктуации сигналов.

Воздействие мультипликативной помехи на передаваемый сигнал s можно рассматривать как модуляцию этого сигнала случайным процессом μ . Такую помеху можно свести к аддитивной:

где — эквивалентная аддитивная помеха, равная Эквивалентная помеха представляется произведением случайного процесса на детерминированную функцию времени s. Это значит, что — нестационарный процесс и что все его распределения и их моменты зависят от времени. Практически это означает, что при анализе нужно после усреднения по множеству прибегать к усреднению по времени. Заметим также, что μ есть случайный процесс с ненулевым средним и что . Процесс имеет уже нулевое среднее и соответственно смещенное распределение. Величины μ и ξ безразмерны, тогда как имеет размерность сигнала.

Эквивалентная мощность мультипликативной помехи, очевидно, будет равна ее дисперсии:

Отношение сигнала к эквивалентной помехе при этом будет равно:

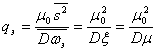(5.76)

т. е. оно определяется только средним значением и дисперсией процесса μ(t), характеризующего мультипликативную помеху.

Распространенным явлением, приводящим к случайным колебаниям параметров сигнала в точке приема, является многолучевое распространение радиоволн. Многолучевость — основная причина замирания сигнала. Вследствие разностей хода лучей, приходящих от передатчика к приемнику, сигнал в приемной антенне представляет собой сумму отдельных колебаний с различными фазами и амплитудами. Интерференция этих колебаний в условиях, когда разности хода лучей не остаются постоянными, и является основной причиной флуктуации как амплитуд, так и фаз составляющих сигнала. В зависимости от ширины спектра сигнала F и свойств канала различают общие (или гладкие) и селективные замирания, которые, в свою очередь, могут быть быстрыми и медленными.

Общие замирания имеют место, когда время запаздывания лучей . При этом коэффициент передачи канала μ (или амплитуда сигнала) и фаза сигнала ф для всех частотных составляющих изменяются одинаково. (При большом числе лучей можно считать, что случайная величина ф имеет равномерную плотность вероятности на интервале от 0 до 2π, а μ- распределение Рэлея

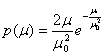(5.77)

где — среднеквадратичное значение коэффициента передачи μ .

В ряде случаев сигнал в точке приема состоит из двух составляющих: регулярной с медленно изменяющимися параметрами и рассеянной быстро флуктуирующей составляющей. В этих случаях коэффициент передачи μ описывается обобщенным распределением Рэлея

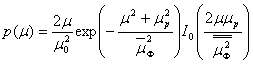(5.78)

где — регулярная составляющая коэффициента передачи, среднее значение квадрата флуктуирующей составляющей, среднее квадратичное значение μ. Фаза сигнала φ в этом случае распределена неравномерно.

В случае сильных замираний, когда , распределение (5.78) приближается к рэлеевскому (5.77). Такие замирания иногда называют рэлеевскими. Замирания, подчиняющиеся обобщенному закону Рэлея, называют квазирэлеевскими.

Для слабых замираний, когда , на основании (5.78) получаем распределение, близкое к нормальному:

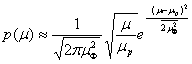
Слабые замирания поэтому называют гауссовыми замираниями.

Согласно экспериментальным данным в диапазонах средних и коротких волн рэлеевские и квазирэлеевские замирания встречаются примерно одинаково часто. В укв диапазоне при дальнем ионосферном или тропосферном распространении преобладают рэлеевские замирания, при ближнем распространении — квазирэлеевские.

Селективные замирания наблюдаются тогда, когда время запаздывания лучей соизмеримо с величиной 1/F. В этом случае амплитуды и фазы частотных составляющих сигнала изменяются независимо друг от друга. При быстрых замираниях амплитуды и фазы смежных элементов сигнала некоррелированы между собой, а при медленных замираниях они изменяются одинаково.

В случае медленных замираний, которые мы и рассмотрим, коэффициент передачи канала μ и фазы сигнала φ практически не изменяются за время длительности нескольких элементов сигнала. Анализ ранее принятых элементов сигнала позволяет с достаточной степенью точности предсказать ожидаемые параметры следующего элемента. В этих условиях прием может быть осуществлен так же, как если бы замирания отсутствовали, и оптимальными будут схемы, рассмотренные в предыдущих параграфах, с той лишь разницей, что в схемах должны производиться непрерывные регулировки μ (регулировка усиления) и φ (регулировка фазы) в соответствии с ожидаемыми значениями μ и φ. В связи с трудностями подстройки фазы более широкое применение находят некогерентные методы приема, в которых сведения о фазе сигнала не используются. В каналах, где случайно изменяется только фаза сигнала, некогерентный прием является оптимальным (см. § 5.6).

Формулы, определяющие вероятность ошибки элемента сигнала при медленных замираниях для данного значения q, остаются теми же, что и в канале без замираний. Но в процессе замираний величина q изменяется пропорционально μ². Поэтому для определения полной вероятности ошибки необходимо усреднить вероятность P( q) в соответствии с распределением р(μ), т. е.

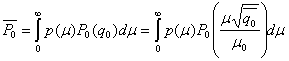(5.79)

где учтено, что .

Найдем в качестве примера вероятность ошибки при когерентном приеме бинарных сигналов в условиях медленных рэлеевских замираний. Подставив в (5.79) выражение для вероятности ошибки (5.53) и плотность вероятности р(μ ) из (5.77), получим

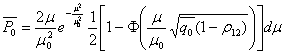
Интегрирование по частям дает следующий результат:

(5.80)

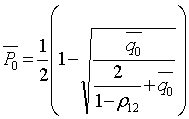(5.80)

При q>>1 имеем приближенную формулу

При некогерентном приеме для систем с активной паузой вероятность ошибки при медленных рэлеевских замираниях определяется путем усреднения (5.71) по μ в соответствии с (5.77)

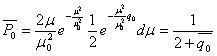(5.81)

График зависимости (5.81) приведен на рис. 5.10. Из сравнения кривых видно, что наличие замираний сигнала значительно снижает помехоустойчивость системы связи.

В случае квазирэлеевских замираний плотность вероятности определяется обобщенным распределением Рэлея (5.78). Для этого случая полная вероятность ошибки при некогерентном приеме бинарных сигналов в соответствии с (5.78), (5.71) и (5.79) будет

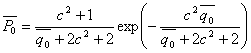(5.82)

где

При с=0 это выражение переходит в ф-лу (5.81) для рэлеевских замирании.

Канал с квазирэлеевскими замираниями является промежуточным случаем между каналом без замираний и каналом с рэлеевскими замираниями. Графики вероятности ошибки для этого случая на рис. 5.10 будут размещаться между кривыми б и в. При малых значениях с графики будут ближе к кривой в, а при больших — к кривой б.

Естественным методом устранения мультипликативной помехи, в том числе и замираний, является применение автоматическойрегулировки усиления (АРУ). При отсутствии аддитивной помехи идеальная система АРУ позволяет полностью устранять мультипликативную помеху. Действие такой системы должно сводиться к умножению сигнала х на , т. е. . При наличии аддитивной помехи Здесь хотя и получается сигнал постоянной интенсивности, но с флуктуирующей по интенсивности аддитивной помехой.

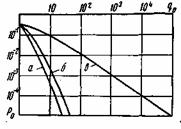
Рис. 5.10. Зависимость вероятности ошибки в бинарной системе с активной паузой от отношения сигнала к помехе: когерентный прием (а), некогерентный прием (б), некогерентный прием в канале с рэлеев-скими замираниями (в)

Эффективной мерой борьбы с замираниями является разнесенный прием сигналов. Суть его состоит в том, что на приеме переданное сообщение воспроизводится не по одному принятому сигналу, а по двум или нескольким сигналам, несущим одно и то же сообщение. Этими сигналами могут быть сигналы нескольких передатчиков, работающих на различных частотах (разнесение по частоте), или сигналы одного и того же передатчика, принятые на различные антенны, разнесенные по пространству или по поляризации. Возможно также и разнесение по времени (например, повторения передачи).

Обработка нескольких сигналов на приеме в общем случае сводится к суммированию с весом. В частных случаях это может быть простое сложение принятых сигналов или выбор наибольшего из них.