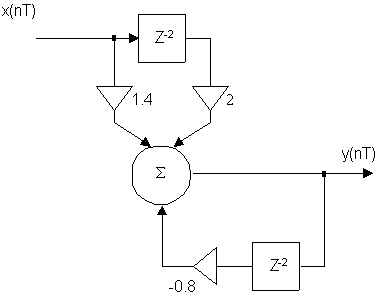
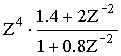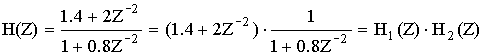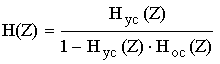Для дискретной цепи общего вида передаточная функция является рациональной функцией и записывается так:

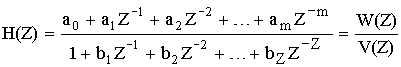
Согласно этому выражению можно сделать заключение общего характера: любая рациональная функция от Z может быть реализована в виде дискретной цепи. Передаточная функция, которая совпадает с заданной рациональной функцией с точностью до постоянного множества Z^Q при условии, что заданная рациональная функция удовлетворяет следующим требованиям:

1. коэффициенты а_i и b_i–вещественные числа.

2. Корни уравнения V(Z)=0 расположены в пределах единичного круга на плоскости Z.

Второе замечание касается устойчивости цепи (цепь устойчива если полюсы H(p) расположены в левой полуплоскости комплексной переменной p, но, при переходе к плоскости Z, левая полуплоскость p отображается на единичный круг плоскости Z.

Пример: Задана рациональная функция (дробная):

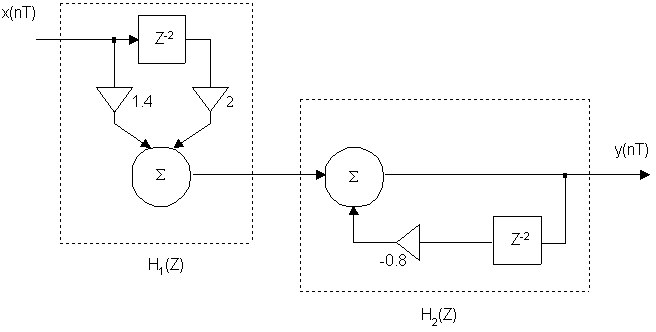
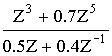Преобразим эту функцию по форме передаточной функции общего вида.

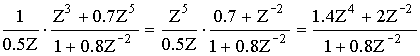
Z⁴= Z^Q

1 + 0.8Z^-2 = 0

Z² + 0.8 = 0

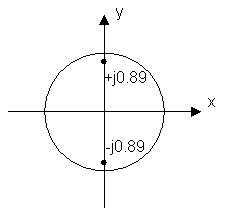
Цепь устойчивая.