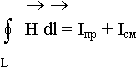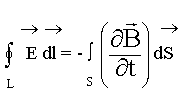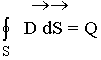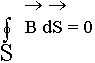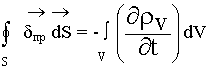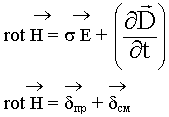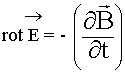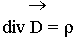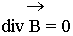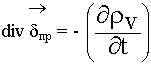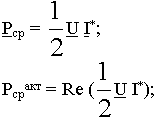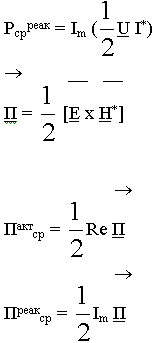1. Основы теории электромагнитного поля
1.1. Информативность различных диапазонов волн
1.2. Диапазон сверхвысоких частот (СВЧ)
1.3. Поля или цепи? Условие квазистационарности
1.4. Векторные характеристики электромагнитного поля
2. Интегральные уравнения электромагнитного поля
2.1. Теорема Гаусса для электрического и магнитного полей
2.2. Закон полного тока. Ток смещения
3. Уравнения Максвелла. Дифференциальные уравнения электромагнитного поля
3.1. Первое уравнение Максвелла
3.2. Второе уравнение Максвелла
3.3. Третье уравнение Максвелла
3.4. Четвертое уравнение Максвелла
4. Энергия электромагнитного поля
5.4. Относительность свойств реальных сред
6. Излучение электромагнитных волн
6.1. Электродинамические потенциалы
6.2. Элементарный электрический излучатель
6.3. Мощность излучения элементарного излучателя. Сопротивление излучения
6.4. Элементарный магнитный излучатель. Принцип перестановочной двойственности
7. Плоские электромагнитные волны
7.1. Понятие волнового процесса
7.2. Плоские волны в идеальной среде
7.3. Плоские волны в реальных средах
8. Плоские ЭМВ на границе раздела двух сред. Волны в неоднородных средах
8.1. Необходимость рассмотрения граничных условий
8.2. Граничные условия для векторов ЭМП
8.3. Отражение электромагнитных волн при нормальном падении на плоскую границу раздела
8.4. Наклонное падение ЭМВ. Формулы Френеля
9. Направляемые электромагнитные волны. Направляющие системы
9.1. Недостатки обычных линий передачи и преимущества волноводов
9.2. Особенности направляемых волн
9.3. Волновые уравнения полей в волноводе произвольного сечения
9.5.1. Основная волна в прямоугольном волноводе. Преимущества волны Н10
9.5.2. Токи в стенках волновода
9.5.3. Передача энергии по волноводу
9.6.1. Волны "Е" - типа в круглом волноводе
9.6.2. Волны "H" - типа в круглом волноводе
9.6.3. Волна Н01 в круглом волноводе. Применения ее в дальней cвязи
10. Линии передачи оптического диапазона
10.2. Основные типы световодов
10.3. Особенности поперечных структур поля в световодах
11. Линии передачи с волной "Т"
11.1. Коаксиальная линия передачи
12.1. Понятие объемного резонатора
12.2. Условие резонанса о объемных резонаторах
12.3. Основные типы объемных резонаторов
12.4. Собственная добротность объемных резонаторов
12.4.1. Нагруженная и внешняя добротности объемных резонаторов
1. Основы теории электромагнитного поля
1.1. Информативность различных диапазонов волн
В последнее время все большее количество людей переходят из сферы материального производства в сферу обработки, хранения и передачи информации. Информацию можно излучать, либо передавать по кабельным линиям, волноводам, световодам и т.д. Количество информации непрерывно растет. Ограничением является количество каналов. Любой канал может передать только определенную информацию.
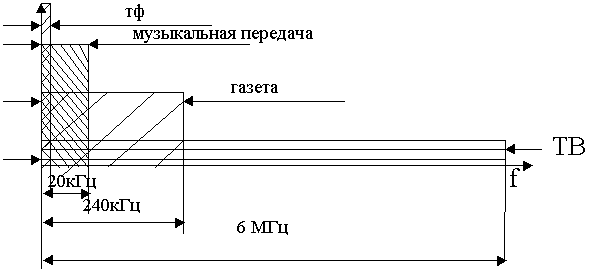
Рассмотрим диапазоны метровых волн (КВ).
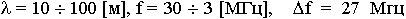
Если в этом диапазоне вести телевидение, то можно организовать четыре канала или 6000 телефонных каналов.
Диапазон УКВ.
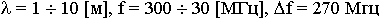
число телевизионных каналов - 40
число телефонных каналов - 6*104
Сантиметровый диапазон:
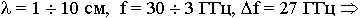
nтелев. = 4000, nтелеф. = 6*106
Миллиметровый диапазон
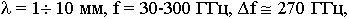
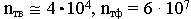
Если посмотреть на оптический диапазон,
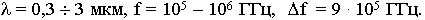
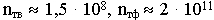
то можно удовлетворить все потребности технического прогресса. С ростом частоты увеличивается информативность. Наращивание каналов связи - это освоение более высокочастотных диапазонов.
1.2. Диапазон сверхвысоких частот (СВЧ)
Диапазон СВЧ : 1 ГГц - 100 Ггц 1 ГГц = 109 Гц
1.2.1. Особенности СВЧ диапазона
- Остронаправленность излучения при сравнительно небольших размерах излучателей.
- Большая информативность.
- Квазиоптический характер распространения волн.
1.3. Поля или цепи? Условие квазистационарности
Аппарат теории цепей есть, он могучий. Зачем нужна теория электромагнитного поля? Противопоставлять теорию цепей и теорию поля нельзя. В одних условиях лучше одна теория, в других другая. Рассмотрим простейшую схему.
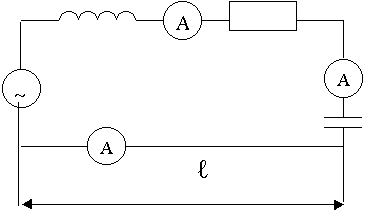
Вопрос: Какие показания будут давать амперметры ? Одинаковые или нет в любой фиксированный момент времени?
Ответ: Да, если Т >> tзап. Запаздыванием процесса колебании от одной точки к другой можно пренебречь. Т - период колебаний источника;
tзап - время запаздывания при распространении сигнала в цепи.
Предположим l - линейные размеры цепи, С - скорость света, тогда tзап = ![]() .
.
Если Т >> ![]()
 Т С >> 1, т.к. Т С =
Т С >> 1, т.к. Т С =  , следовательно:
, следовательно:
 >> 1 - условие квазистационарности. (1.3.1.)
>> 1 - условие квазистационарности. (1.3.1.)
Если условие квазистационарности выполняется, то можно пользоваться теорией цепей. Когда условие квазистационарности не выполняется, нужен другой анализ. В сантиметровом и оптическом диапазонах используется теория поля.
1.4. Векторные характеристики электромагнитных полей
Для полного описания свойств электромагнитных полей нужно знать положение, величину и направление в пространстве четырех векторов.
 - вектор напряженности электрического поля.
- вектор напряженности электрического поля.
 (х, у,z,t)
(х, у,z,t)  [В/м]
[В/м]
 - вектор электрического смещения
- вектор электрического смещения
 (x,y,z,t)
(x,y,z,t)  [кл/м2]
[кл/м2]
 - вектор напряженности магнитного поля.
- вектор напряженности магнитного поля.
 (х,у,z,t)
(х,у,z,t) 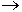 [А/М]
[А/М]
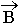 - вектор магнитной индукции
- вектор магнитной индукции
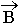 (x,y,z,t)
(x,y,z,t) 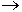 [Вб/м2]
[Вб/м2]
 ,
, 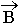 - характеризуют силовые характеристики полей.
- характеризуют силовые характеристики полей.
 ,
,  - характеризуют источники ЭМП
- характеризуют источники ЭМП
1.5. Материальные уравнения среды
Материальные уравнения устанавливают связь между векторными характеристиками электромагнитных полей одинаковой природы. Рассмотрим связь между векторами D и Е, В и Н.
Электромагнитные процессы могут протекать в самых разных условиях. Электромагнитные волны пронизывают ионосферу (от спутника до земной антенны). От свойств среды, зависят условия распространения. Физики подробно дают ответ на такие вопросы (физика твердого тела, физика плазмы и т.д.). В простом представлении (грубая модель) среды
разделяют на диэлектрические и магнитные. Диэлектрические среды состоят из зарядов одинаковой величины и противоположных по знаку (диполей).
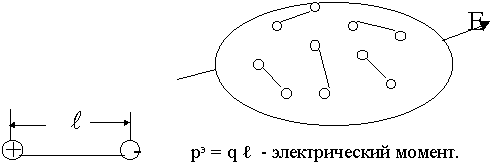
Многочисленные эксперименты и строгие теоретические выводы подтверждают связь:
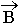 =
=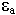

где 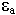 - абсолютная диэлектрическая проницаемость среды.
- абсолютная диэлектрическая проницаемость среды.
Для вакуума 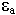 =
= 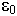 = 8,85 * 10-12 [Ф/м].
= 8,85 * 10-12 [Ф/м].
Вводят понятие относительной диэлектрической проницаемости: 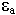 =
= 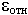
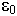
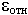 =
= ![]()
В справочной литературе указаны значения 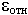 . Для магнитных веществ ситуация аналогичная:
. Для магнитных веществ ситуация аналогичная:
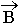 =
= 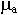

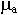 - абсолютная магнитная проницаемость.
- абсолютная магнитная проницаемость.
Для вакуума:
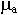 =
= 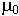 = 4
= 4  * 10-7
* 10-7 ![]()
Для удобства расчетов вводят понятие относительной магнитной проницаемости :
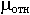 =
= ![]()
Выражения (1.5.1.) называют материальными уравнениями среды.
 =
= 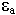

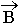 =
= 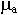

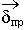 =
= 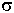

(1.5.1.)
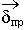 - плотность тока проводимости [
- плотность тока проводимости [![]() ]
]
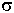 - удельная проводимость среды [
- удельная проводимость среды [![]() ].
].
1.6. Методы описания физических явлений и расчета устройств СВЧ диапазона
- Электродинамика, как основа описания физических явлений в СВЧ диапазоне.
- Уравнения Максвелла, как обобщение экспериментальных законов электричества и магнетизма.
2. Интегральные уравнения электромагнитного поля
2.1. Теорема Гаусса для электрического поля
Интегральные уравнения электромагнитного поля являются обобщением экспериментальных законов и являются постулатами.
Теорема Гаусса устанавливает связь между потоком вектора электромагнитной индукции ![]() , проходящим через замкнутую поверхность S и зарядами находящимися внутри поверхности. Теорема Гаусса является обобщением закона Кулона.
, проходящим через замкнутую поверхность S и зарядами находящимися внутри поверхности. Теорема Гаусса является обобщением закона Кулона.
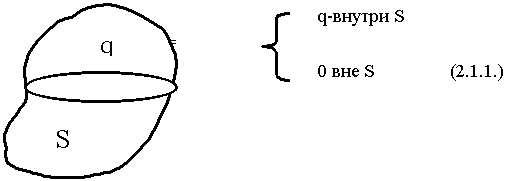
Если заряд вне поверхности, то П = 0, т.к. сколько зарядов вошло, столько и вышло.
Внутри заряженной поверхности могут быть самые разные распределения зарядов.
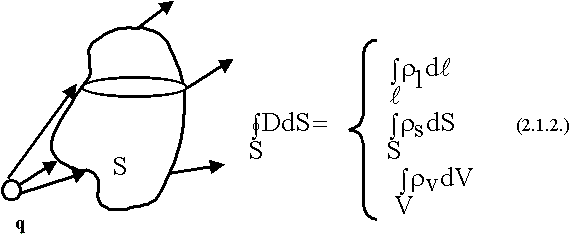
Физическое понимание этих соотношений роль и сила теоремы Гаусса. Она позволяет судить о процессах происходящих внутри не проникая туда. К примеру, поток 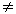 0, значит, внутри S есть что-то, что создает поток. Если П=0, то там ничего нет, нет источников полей.
0, значит, внутри S есть что-то, что создает поток. Если П=0, то там ничего нет, нет источников полей.
Практическое использование теоремы Гаусса, рекомендации. Форма поверхности произвольная. Любая. Как распорядиться свободой ? Цилиндр, сфера, куб и т.д. Разные поверхности, разные сложности. Универсальная рекомендация. Если поверхность выбрана таким образом, что вектор ![]() будет постоянен, то можно использовать теорему Гаусса.
будет постоянен, то можно использовать теорему Гаусса.
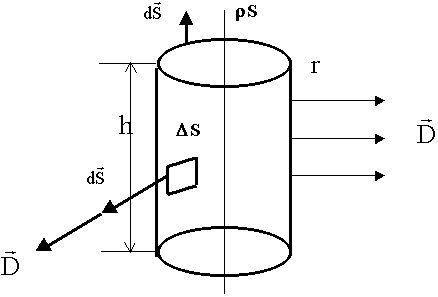
Пример: Рассчитать вектор ![]() , создаваемый бесконечно длинной заряженной нитью с линейной плотностью
, создаваемый бесконечно длинной заряженной нитью с линейной плотностью 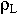 .
.
По теореме Гаусса (2.1.2.) имеем:
![]()
 d
d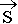 = q
= q
Этап 1. Выбор замкнутой поверхности. Цилиндр высотой h и радиусом r.
Этап 2. Вычисление потока вектора  :
:
![]()
 d
d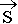 = 2
= 2 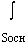
 d
d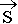 +
+ 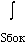
 d
d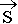 =
=  2
2  r h
r h
Этап 3. Вычисление заряда:
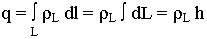
Этап 4. Применение теоремы Гаусса:
 2
2  r h =
r h = 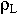 h ;
h ;
 = (
= (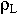 / 2
/ 2  r) r0
r) r0
2.1.1. Теорема Гаусса для магнитных полей
Устанавливает связь между потоком вектора  и источниками магнитного поля. Магнитных зарядов в природе нет.
и источниками магнитного поля. Магнитных зарядов в природе нет.
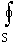
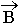 d
d 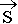 = 0 (2.1.1.1.)
= 0 (2.1.1.1.)
Cто лет назад этими двумя интегральными уравнениями ограничивались познания человечества о природе.
2.2. Закон полного тока. Ток смещения
К середине 18 столетия большинство ученых пришли к выводу, что между магнитными и электрическими явлениями нет ничего общего, это разные явления. К началу 19 века накопились факты, утверждающие, что существует связь между электрическими и магнитными явлениями. Датский ученый Эрстед сделал открытие, описав явление, но объяснение этого явления тогда было неправильно. Факт - если пропустить по проводнику электрический ток, то в окружающем пространстве возникает вихревое магнитное поле ![]() , направленное по касательной. Стрелка компаса отклоняется.
, направленное по касательной. Стрелка компаса отклоняется.
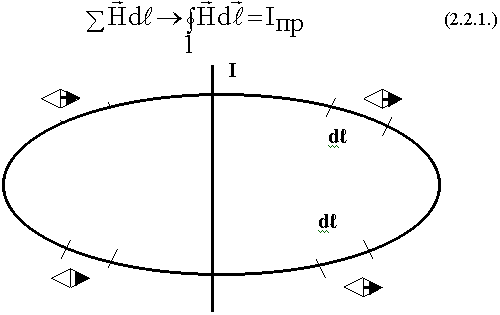
Физический смысл: Источниками магнитных полей являются движущееся заряды, т.е. ток.
Введем понятие плотности электрического тока 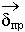 - количество зарядов, проходящих в единицу времени, через единичную площадку
- количество зарядов, проходящих в единицу времени, через единичную площадку 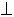 к ней направленную.
к ней направленную.
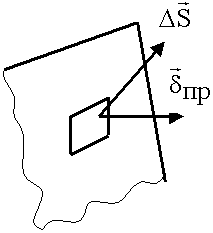
На площадке S выделим элемент площадью 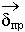 S, покажем направление площади и плотность тока проводимости:
S, покажем направление площади и плотность тока проводимости: 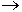
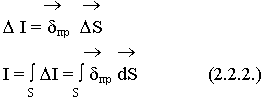
В некоторой ситуации имеет место сложное распределение тока.
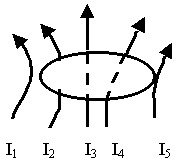
Выделим в системе некоторый контур L, охватывающий часть токов. Вклад в циркуляцию вектора  дают только токи, охватывающие выделенный контур:
дают только токи, охватывающие выделенный контур:
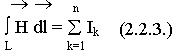
Для среды с непрерывным распределением тока:
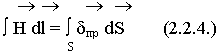
Магнитное поле могут создавать не только движущиеся заряды, но и переменное электрическое поле.
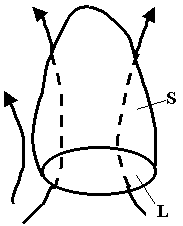
2.2.1. Ток смещения
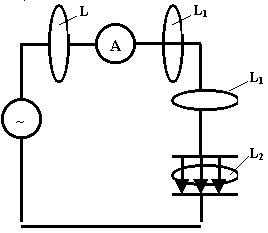
Попытаемся на различных участках этой цепи вычислить циркуляцию вектора  .
.
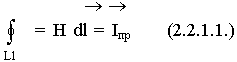
Передвинем постепенно контур L1 к обкладкам конденсатора. Описанное равенство пока выполняется.
Неверно 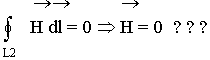
Магнитное поле ведь было до обкладок, почему же оно исчезло?
Максвелл показал, что магнитное поле есть, его порождает переменное электрическое поле что между обкладками есть ток смещения.
По Максвеллу:
правильно 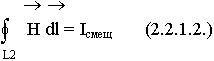
В общем случае могут протекать как токи проводимости, так и токи смещения.
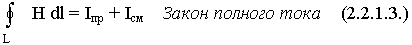
Если ввести понятие плотности тока смещения, то:
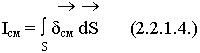
Рассчитаем плотность тока смещения в цепи:
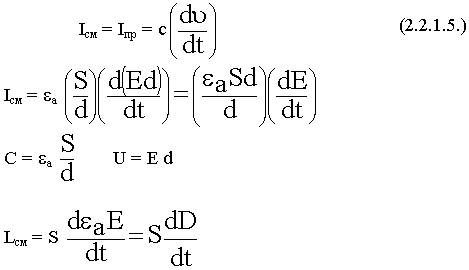
2.3. Закон электромагнитной индукции
Устанавливает в интегральной форме зависимость ЭДС, наведенной в контуре от магнитного потока. Сформулировал закон электромагнитной индукции Фарадей.

Площадка S опирается на контур L
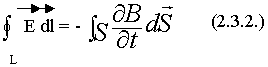
Знак (-) говорит о том, что возникшая в контуре ЭДС будет создавать переменное магнитное поле, которое препятствует направлению основного поля, которое вызвало ЭДС.
2.4. Закон сохранения заряда
В замкнутой системе при любых процессах полный заряд остается неизменным. Если заряд остается неизменным, значит ничего не вышло за пределы. Если заряд меняется, значит возникает ток:
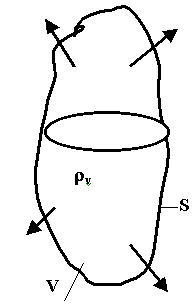
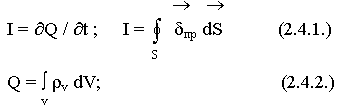
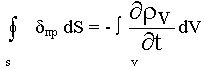 - уравнение непрерывности полного тока.
- уравнение непрерывности полного тока.
3. Уравнения Максвелла. Дифференциальные уравнения электромагнитного поля
Интегральные уравнения не позволяют получать информацию об электромагнитных процессах в каждой точке пространства. Они дают усредненные решения полей в пространстве.
Хорошо развитый аппарат математических решений позволят переходить от интегральной формы к дифференциальным решениям.
Впервые переход от интегральных уравнений к дифференциальным сделал Максвелл.
3.1. Первое уравнение Максвелла
Первое уравнение Максвелла является дифференциальной формулировкой закона полного тока:
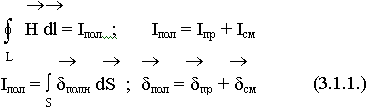
S - опирается на контур L.
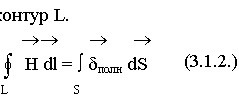
Используем теорему Стокса:
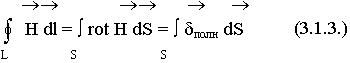
Равенство сохраняет силу по любой поверхности, опирающейся на контур L, отсюда следует, что подинтегральные функции равны.
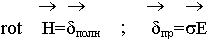 - дифференциальная форма закона Ома.
- дифференциальная форма закона Ома.
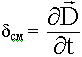
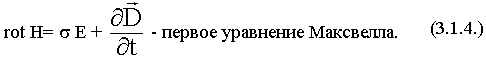
Физический смысл 1-го уравнения Максвелла.
Источниками вихревых магнитных полей являются токи проводимости и токи смещения.
3.2. Второе уравнение Максвелла
Второе уравнение Максвелла является дифференциальной формулировкой закона электромагнитной индукции:
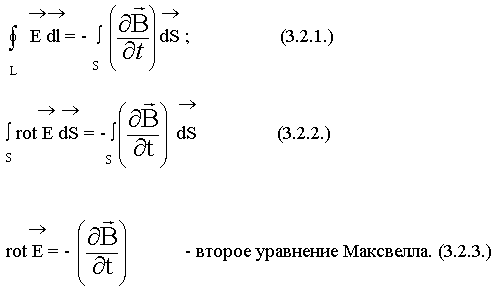
Физический смысл. Вихревое электрическое поле создается переменным магнитным полем.
3.3. Третье уравнение Максвелла
Третье уравнение Максвелла является дифференциальной формулировкой теоремы Гаусса для электрических полей.
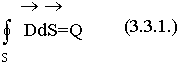
Воспользуемся теоремой Остроградского-Гаусса, которая позволяет осуществить переход от
поверхностного интеграла П ( ) к объемному интегралу от (div D):
) к объемному интегралу от (div D):
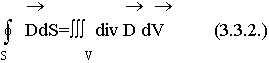
Запишем правую часть уравнения (3.3.1.) для объемного заряда. Объединим два выражения:
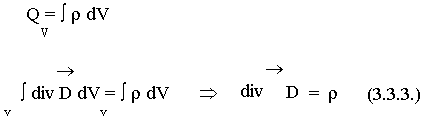
- третье уравнение Максвелла. (3.3.3.)
Физический смысл. Источниками электрического поля (векторов Е и D) являются заряды с плотностью r .
3.4. Четвертое уравнение Максвелла
Четвертое уравнение Максвелла является дифференциальной формулировкой теоремы Гаусса для магнитных полей:

Физический смысл. Дивергенция вектора 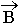 любой точке пространства равняется нулю, т.е. - источников нет (магнитные заряды в природе отсутствуют). Нет ни стоков, ни источников.
любой точке пространства равняется нулю, т.е. - источников нет (магнитные заряды в природе отсутствуют). Нет ни стоков, ни источников.
3.5. Закон сохранения заряда в дифференциальной форме
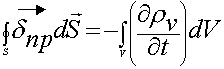
Используем теорему Остроградского-Гаусса:
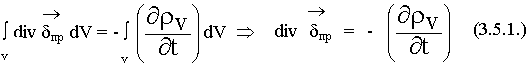
- это уравнение является следствием из предыдущих уравнений
3.6. Таблица интегральных и дифференциальных уравнений электромагнитного поля
Материальные уравнения среды.
 =
= 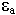

Все эти уравнения являются обобщением в математической форме опытов всего человечества об электромагнитных явлениях. Они не доказываются и не выводятся - это результат опытов.
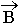 =
= 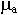

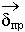 =
= 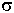

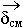 =
= 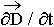
|
Интегральные уравнения электромагнитного поля |
Дифференциальные уравнения электромагнитного поля. Уравнения Максвелла |
|
1. Закон полного тока:
2. Закон электромагнитной индукции:
3. Теорема Гаусса для электрических полей:
4. Теорема Гаусса для магнитных полей:
5. Закон сохранения заряда
|
|
4. Энергия электромагнитного поля
4.1. Уравнение баланса энергии
Баланс энергии ЭМП является следствием закона сохранения энергии для ЭМП. Выберем произвольный объем, ограниченный поверхностью S, внутри находятся источники ЭМП.
Считаем, что мощность источников нам известна, обозначим ее Рст (сторонняя).
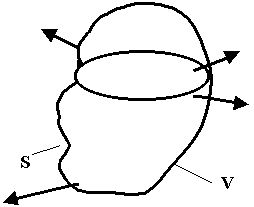
Природа сторонних источников не рассматривается. Выясним, на какие процессы расходуется Рст :
1) Часть Рст преобразуется в другие виды энергии (тепло и т.д.). Это мощность Рпот.
2) Внутри V могут находиться элементы, которые запасают энергию. Для характеристики этих процессов вводится понятие плотности энергии ЭМП WЭМ, удельная мощность 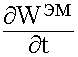 По всему объему:
По всему объему:
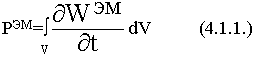
РЭМ - мощность расходуемая на изменение накопленной внутри объема энергии ЭМП.
3) С ЭМП связаны процессы переноса энергии.
Эта часть Р называют излучаемой Ризл. Для характеристики таких процессов введем понятие плотности энергии переносимой ЭМП через единичную поверхность за единицу времени в перпендикулярном поверхности направлении. Эта величина получила название вектора Пойнтинга 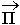 и характеризует количество энергии переносимой через единичную площадку за единицу времени ^ поверхности:
и характеризует количество энергии переносимой через единичную площадку за единицу времени ^ поверхности:
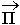 [Вт/м2]
[Вт/м2]
Мощность излучения:
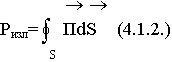
В силу закона сохранения энергии имеем:
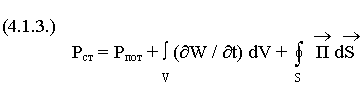 - уравнение баланса энергии.
- уравнение баланса энергии.
Пример:
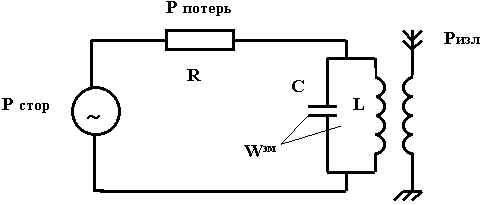
4.2. Теорема Пойнтинга
Теорема Пойнтинга устанавливает количественную связь между векторными характеристиками полей и отдельными составляющими баланса энергии ЭМП.
Для установления этой связи воспользуемся уравнениями Максвелла:
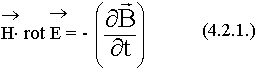
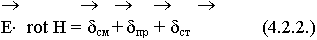
Вычтем (4.2.2.) из (4.2.1.):
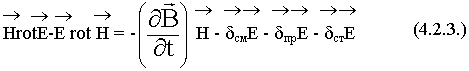
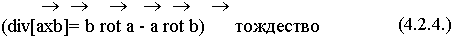
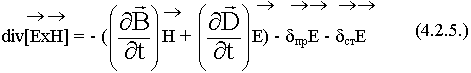
Закон сохранения энергии это интегральное соотношение. Поэтому выполним интегрирование последнего уравнения по объему V:
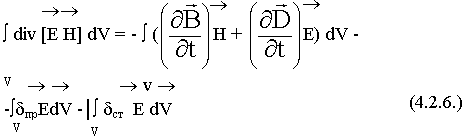
по теореме Остроградского-Гаусса:
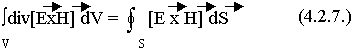
Упростим выражение под знаком объемного интеграла:
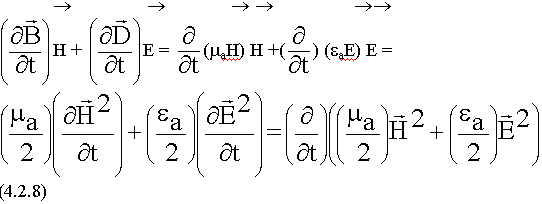
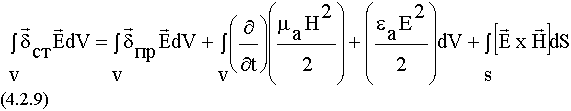
Сравним последнее уравнение с составляющими баланса энергии ЭМП (4.1.2.):
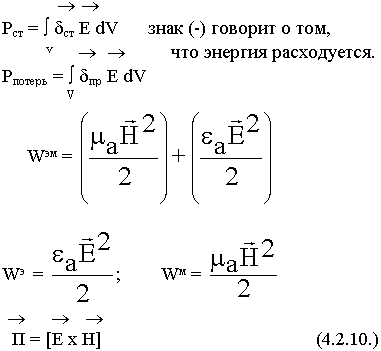
4.3. Некоторые примеры
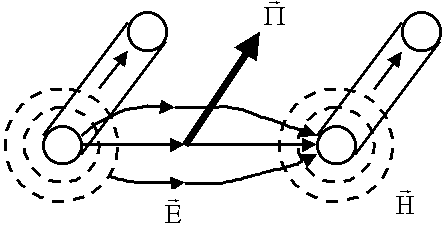
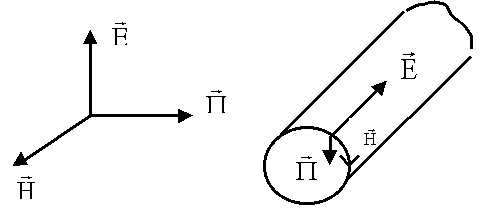
Для определения направления переноса энергии необходимо определить направления 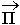 . В соответствии с правилами векторного произведения направление вектора
. В соответствии с правилами векторного произведения направление вектора 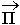 , перпендикулярно плоскости векторов
, перпендикулярно плоскости векторов  и
и  . Основная энергия, переносимая вдоль линии, распределена вне проводов. Можно показать, что энергия, поступающая внутрь провода в точности равна джоулевым потерям.
. Основная энергия, переносимая вдоль линии, распределена вне проводов. Можно показать, что энергия, поступающая внутрь провода в точности равна джоулевым потерям.
Любое реальное сообщение связано с передачей электромагнитной энергии. Чувствительность приемных устройств оценивается по той минимальной энергии, которой необходимо для того, чтобы эти устройства срабатывали.
Установим правило по которому можно рассчитывать энергию электромагнитного поля, если известны  и
и  ,
,  и
и 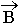 (векторные характеристики).
(векторные характеристики).
Уравнения Максвелла дают в целом полное описание уравнений. Любой акт проверки неизбежно связан с извлечением энергии ЭМП. Для сравнения экспериментальных и теоретических результатов необходимо связать энергию с напряженностью полей (векторные характеристики ЭМП).
5. Классификация ЭМП
В основе классификации ЭМП лежат 2 критерия:
- Зависимость полей от времени.
- Соотношение между токами проводимости и смещения.
5.1. Статические поля
Статические поля не зависят от времени :
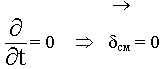
Заряды неподвижные 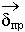 = 0.
= 0.
Уравнения Максвелла:
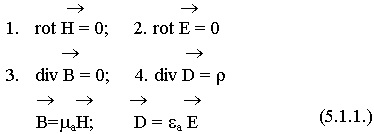
В статических полях электрические и магнитные явления проявляют себя независимо. Уравнения Максвелла распадаются на 2 системы:
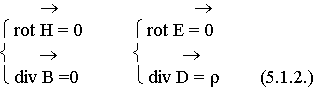
5.2. Стационарные поля
Стационарные поля не зависят от времени ![]() =0
=0 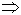
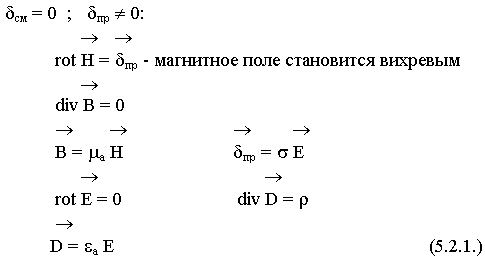
Поля зависят друг от друга. Электрическое поле не вихревое, магнитное вихревое.
5.3. Квазистационарные поля
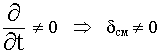 Процессы медленно изменяются во времени.
Процессы медленно изменяются во времени.
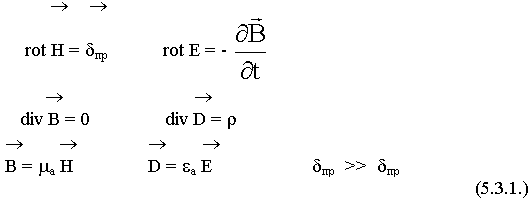
Эти поля детально изучаются в ТЭЦ.
5.4. Относительность свойств реальных сред
В реальных средах существуют токи проводимости и токи смещения. Рассмотрим поведение реальных сред в переменных полях.
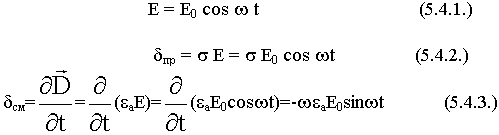
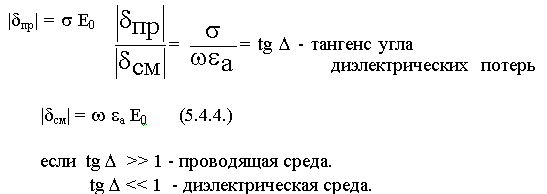
С ростом частоты все среды тяготеют к диэлектрикам.
5.5. Быстропеременные поля
5.5.1. Гармонические процессы и метод комплексных амплитуд
Из-за того, что процесс очень быстро изменяется по времени, то :
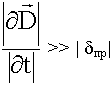 (производные по времени большие)
(производные по времени большие)
Уравнения Максвелла принимают вид:
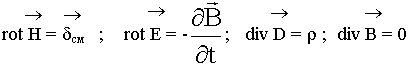 (5.5.1.1.)
(5.5.1.1.)
В дальнейшем в курсе мы будем иметь дело с таким классом полей, т.е. быстропеременным. Из всего многообразия временных зависимостей полей в нашем курсе мы рассмотрим группу, где поля изменяются по гармоническому закону:
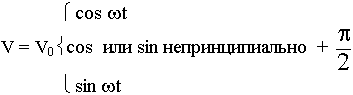
Метод комплексных амплитуд имеет те же предположения, что и в курсе ТЭЦ, мы несколько распространим его на векторные величины.
V = V0 cos w t - в общем виде записана производная векторная величина, изменяющаяся по гармоническому закону.
Как выражается такая величина в методе комплексных амплитуд ?
V = V0 cos w t 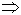 V = V0 e j w t - временная зависимость.
V = V0 e j w t - временная зависимость.
Как вернуться к исходному вектору без точки? Какая теорема используется ? Теорема Эйлера.
V = Re V = V0 cos w t
V = V0 cos (w t + j ) 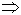 V = V0 e j( w t + j) = V0 e jw t
V = V0 e j( w t + j) = V0 e jw t
V0 = V0 e j j В этом методе на амплитуду ничего не действует.
Вывод:
- В окончательных выражениях зависимость от времени исчезает, хотя она всегда известна, ее можно восстановить.
- Значительно упрощается дифференцирование и интегрирование по времени, дифференцируем
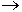 умножаем на jw , интегрируем
умножаем на jw , интегрируем 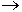 делим на jw
делим на jw
![]() = V0 jw e jw t = V jw
= V0 jw e jw t = V jw
Средняя мощность:
5.5.2. Комплексные уравнения Максвелла
Комплексные уравнения Максвелла являются дифференциальной формой законов электромагнетизма для гармонических процессов:
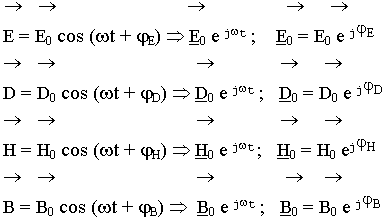 (5.5.2.1.)
(5.5.2.1.)
Применим метод комплексных амплитуд к этому процессу:
 =
= 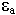

Формально можно записать, хотя деление векторов не встречается.
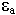 =
=![]() ;
;
где 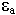 - комплексная диэлектрическая проницаемость
- комплексная диэлектрическая проницаемость
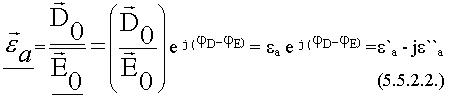
В общем случае фаза, с которой изменяется вектор  и вектор
и вектор  могут неравны
могут неравны 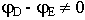 , т.е. возможно опережение или отставание.
, т.е. возможно опережение или отставание.
В гармонических полях абсолютная диэлектрическая и магнитная проницаемости величины комплексные:
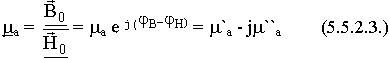
Площадь петли равна энергии на перемагничевание. В любых магнитных материалах имеется запаздывание вектора 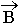 относительно
относительно  .
.
Уравнения Максвелла
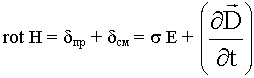 - в обычной дифференциальной форме.
- в обычной дифференциальной форме.
Покажем, что уравнения Максвелла относительно временных процессов являются линейными.
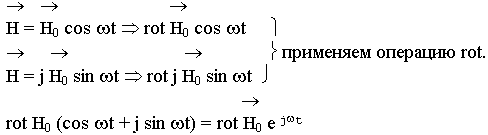
Применим первое уравнение Максвелла к векторным характеристикам полей, записанных в комплексной форме:
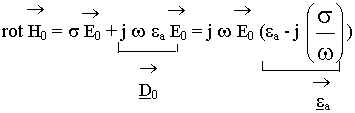 (5.5.2.4.)
(5.5.2.4.)
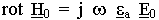 в комплексной форме отсутствует зависимость от времени.
в комплексной форме отсутствует зависимость от времени.
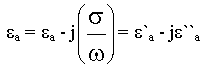
где: 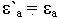 - характеризует процессы поляризации.
- характеризует процессы поляризации.
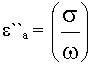 - характеризует джоулевые потери.
- характеризует джоулевые потери.
По аналогии второе уравнение Максвелла:
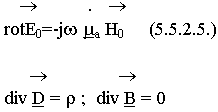
Третье и четвертое уравнения не реагируют на время, не зависят от того, какой процесс гармонический или нет.
Для гармонических процессов третье и четвертое уравнения теряют смысл, они входят в первое и второе.
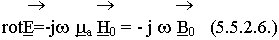
Применим к правой и левой части уравнения (5.5.2.6.) операцию div:
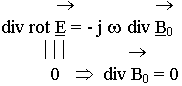
Метод комплексных амплитуд позволил существенно упростить описание полей, т.к. требуется только два уравнения:
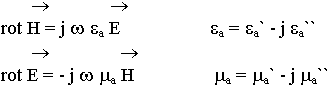
В дальнейшем черточку опускаем, но всегда имеем в виду, что комплексная форма, т.к. присутствует символ j.
6. Излучение электромагнитных волн
6.1. Электродинамические потенциалы
Рассмотрим четвертое уравнение Максвелла ![]() . Формально в соответствии с правилами векторного анализа:
. Формально в соответствии с правилами векторного анализа:
![]()
(6.1.1)
на основании этого тождества вектор ![]() можно представить как rot другого любого вектора
можно представить как rot другого любого вектора ![]() :
:
![]()
(6.1.2)
Возьмем второе уравнение Максвелла:
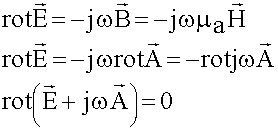 (6.1.3)
(6.1.3)
Появился новый вектор, rot которого равен нулю.
![]() - тождество известное. (6.1.4)
- тождество известное. (6.1.4)
Мы можем утверждать, что выражение в скобках есть градиент.
![]() (6.1.5)
(6.1.5)
![]() (6.1.6)
(6.1.6)
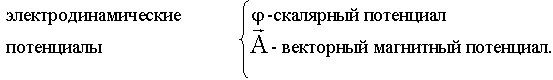
Можно найти уравнения, из которых определяются ![]() и
и  .
.
На f для постоянного тока при w = 0 вклад в электрическое поле от вектора ![]() не происходит:
не происходит:
![]()
(6.1.7)
Для статистических и стационарных процессов электрическое поле представляется как градиент некоторой скалярной функции  .
.
В случае переменных полей:
![]()
(6.1.8)
Получим уравнение для определения величин  и
и ![]() . Воспользуемся первым уравнением Максвелла, через
. Воспользуемся первым уравнением Максвелла, через ![]() обозначим сторонние
обозначим сторонние
источники: ![]()
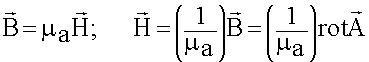
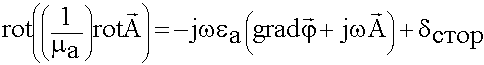 (6.1.9)
(6.1.9)
![]() (6.1.10)
(6.1.10)
Используем тождество:
![]() (6.1.11)
(6.1.11)
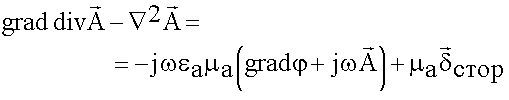
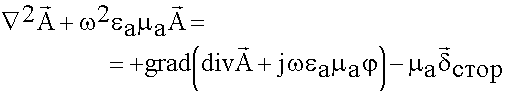 (6.1.12)
(6.1.12)
Для упрощения уравнений используем свойство электродинамических потенциалов – их неоднозначность:
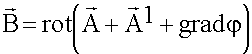 (6.1.13)
(6.1.13)
В силу неоднозначности мы можем ввести требование. Налагаем дополнительное требование:
![]() калибровочное соотношение (6.1.14)
калибровочное соотношение (6.1.14)
для электродинамических потенциалов. Это соотношение имеет четкий физический смысл. Строго можно доказать, что соотношение является другой записью закона сохранения заряда. Все другие допустимые соотношения будут противоречить закону сохранения заряда (требуется дополнительное время для доказательства).
![]() - неоднородное волновое уравнение
- неоднородное волновое уравнение
Гельмгольц ![]() для
для ![]() (6.1.15)
(6.1.15)
Получим по такой же схеме второе соотношение из второго уравнения Максвелла:
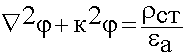 - неоднородное волновое уравнение Гельмгольца для
- неоднородное волновое уравнение Гельмгольца для  . (6.1.16)
. (6.1.16)
При отсутствии источников ЭМП, правая часть обращается в 0, уравнения будут однородными, их называют уравнениями Гельмгольца. Не решая уравнений, мы будем записывать решение исходя их физического смысла.
Источниками ЭМП являются заряды, 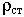 распределенные в некоторой области V. Найдем потенциал в точке М. Выделим элементарный объем заряженного тела. Найдем потенциал, который создает этот объем.
распределенные в некоторой области V. Найдем потенциал в точке М. Выделим элементарный объем заряженного тела. Найдем потенциал, который создает этот объем.
Объем настолько мал, что заряд можно считать точечным.
Полный потенциал  найдем как
найдем как 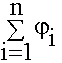
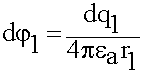 ;
;
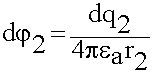 ;
;
![]()
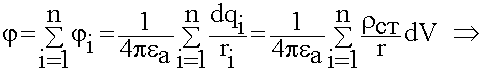
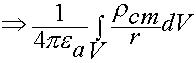
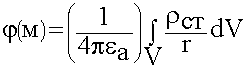 (6.1.17)
(6.1.17)
Распределение потенциала не зависит от времени.
Некоторое тело содержит заряды 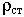 , имеющие зависимость от времени. При расчете изменяющихся от времени процессов необходимо учитывать конечную скорость распространения. Момент времени регистрации будет другим:
, имеющие зависимость от времени. При расчете изменяющихся от времени процессов необходимо учитывать конечную скорость распространения. Момент времени регистрации будет другим:
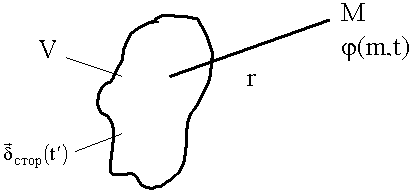
![]()
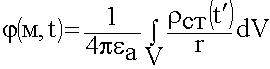
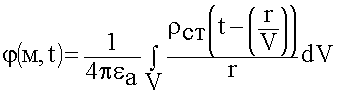
(6.1.18)
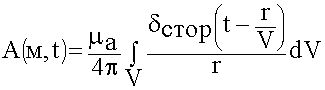
Решение волновых уравнений, их называют запаздывающими электродинамическими потенциалами.
6.2. Элементарный электрический излучатель
Рассмотрим простейший источник, короткая проволока с переменным током.
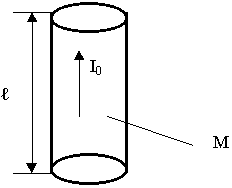
Под элементарным электрическим излучателем будем понимать проводник достаточно малых размеров по сравнению с 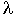 с равномерным по амплитуде распределения тока. Будем считать, что излучатель находится в безграничном пространстве, в идеальной среде без потерь (вакуум). При расчете полей введем ограничения:
с равномерным по амплитуде распределения тока. Будем считать, что излучатель находится в безграничном пространстве, в идеальной среде без потерь (вакуум). При расчете полей введем ограничения:
- безограниченная среда (вакуум)
- 1 < <
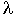 , такое условие позволяет пренебречь запаздыванием внутри излучателя, т.е. амплитуда тока постоянна, хотя ток переменный. На концах диполя будут скапливаться заряды.
, такое условие позволяет пренебречь запаздыванием внутри излучателя, т.е. амплитуда тока постоянна, хотя ток переменный. На концах диполя будут скапливаться заряды. - r > > 1 размеры излучателя много меньше расстояний, на которых определяются потенциалы.
- переменный ток в излучателе изменяется по гармоническому закону.
Если разобраться с полями, которые создает элементарный излучатель, то можно рассчитать поля самой сложной антенны. Расчет полей элементарных излучателей будем проводить в сферической системе координат.
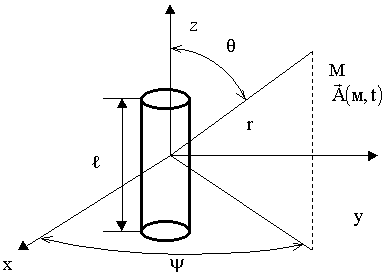
Этапы решения:
-
- Определение векторного электродинамического потенциала, создаваемого излучателем
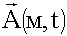 .
. - Определение вектора Н.
- Определение векторного электродинамического потенциала, создаваемого излучателем
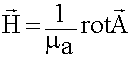
- Определение электрического поля из второго уравнения:

Расчет полей элементарного излучателя
Первый этап:
Расчет вектора 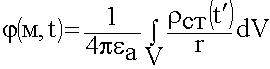
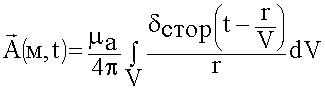
Как использовать данный результат к элементарному проводу?
Используем сферическую систему координат.
r > > 1, т.к. r очень большое, и примерно везде одинаково, выносим за знак интеграла:
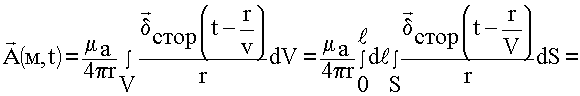
![]()
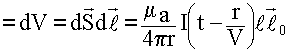

![]() - умножение необходимо на единичный вектор, т.к. ток имеет направление.
- умножение необходимо на единичный вектор, т.к. ток имеет направление.
Поскольку процессы гармонические, необходимо ввести зависимость от времени:
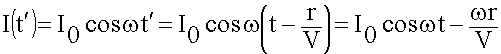
![]() (обозначим). Это строго можно показать!
(обозначим). Это строго можно показать!
В теме “Плоские волны” будет сделано.
![]()
С учетом всех обозначений переходим к комплексным выражениям:
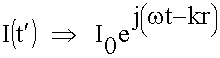
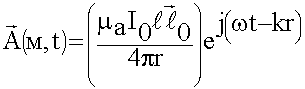
Из общих выражений, которые дает теория, мы получили конечный результат.
Второй этап. Определение магнитных полей.
![]() - определяем вектор
- определяем вектор ![]() , т.е. магнитное поле.
, т.е. магнитное поле.
![]() ;
; 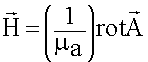 ;
; 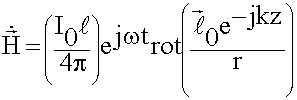
окончательный результат. Из 3-х составляющих, который определяют rot, отличный от 0 будет только азимутальная составляющая Нy . Не решая:
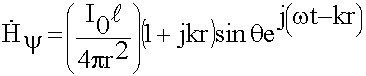
Нr = Hq = 0 (6.2.1)
Третий этап: Нахождение электрических полей.
rot![]() (первое уравнение Максвелла)
(первое уравнение Максвелла)
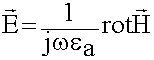
Запишем составляющие электрического поля, их две:
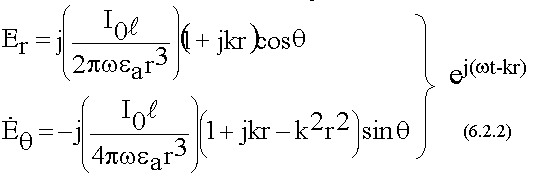
Формулы запоминать не надо, они нужны для дальнейшего анализа.
Для элементарного излучателя характерно наличие 3-х составляющих полей
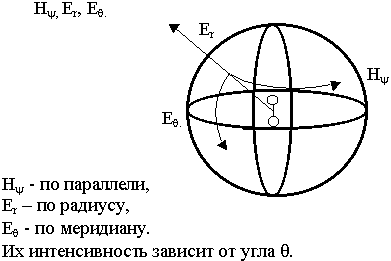
Элементарный излучатель создает в окружающем пространстве сферическую волну, поверхностью равных фаз является сфера.
6.2.1. Ближняя и дальняя зона электрического излучателя
Критерием для ближней и дальней зоны является величина kr. Если kr < < 1, то ближняя зона, если kr > > 1 – дальняя зона.
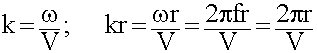 ; kr << 1
; kr << 1 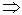 r < <
r < < 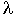
В ближней зоне расстояние r < < 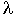 .
.
В дальней зоне расстояние r > > 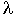 . (6.2.1.1)
. (6.2.1.1)
Поля в ближней зоне
- kr < < 1 анализируем общие выражения.
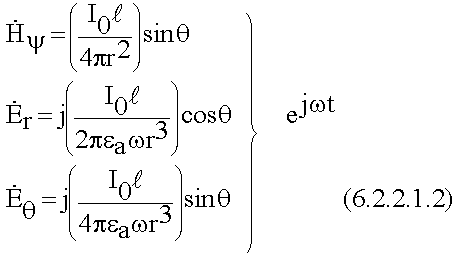
Анализ:
- Поля очень быстро уменьшаются с удалением от излучателя.
- Электрические и магнитные поля отличаются на множитель j, если в такой то момент магнитное поле max, то электрическое поле минимально, т.е. электрическое и магнитное поле по фазе сдвинуто на 900.
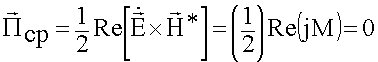
В ближней зоне процесс протекает, но ничего не изменяется, не излучается, колебательный процесс, пол периода поля как бы отрываются от излучателя, полпериода вновь возвращается.
Поля в дальней зоне.
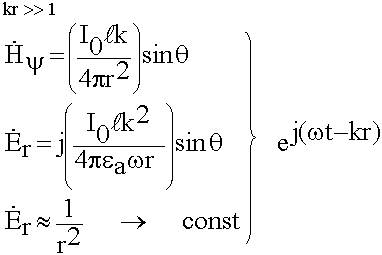
Анализ. Радиальная составляющая изменяется обратно пропорционально квадрату расстояния ![]() , поэтому в дальней зоне она очень мала
, поэтому в дальней зоне она очень мала 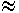 0.
0.
![]()
Составляющие 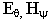 убывают более медленно с расстоянием
убывают более медленно с расстоянием ![]() .
.
С ростом частоты напряженности поля увеличиваются при прочих равных условиях. В дальней зоне отношение
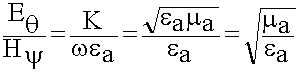
определяется только параметрами среды и называется характеристическим волновым сопротивлением. По размерности это ОМ.
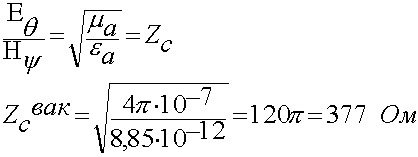
Пример:
Если замерили напряженность магнитного поля в дальней зоне Н = 1 А/м, Е = 377 В/м.
По мере удаления от излучателя сферическая волна переходит в плоскую. В дальней зоне будет плоская электромагнитная волна.
Направленность излучения. Интенсивность излучения зависит от угловых координат.
Графическое изображение распределения в пространстве электрического (магнитного) полей в полярных координатах называется диаграммой направленности.
6.3. Мощность излучения элементарного излучателя
Вопросы по мощности излучения автоматически решаются, если определены составляющие полей. Расчет имеет смысл только в дальней зоне:
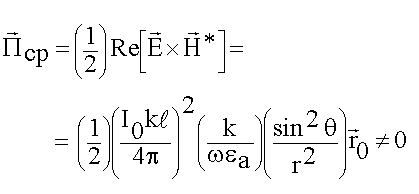 (6.3.1)
(6.3.1)
В дальней зоне излучатель излучает. Не странно ли? В ближней зоне Пср = 0, а в дальней зоне Пср  0. Фаза в ближней зоне 900, а в дальней зоне они совпадают. Излучение вызвано тем, что электрические и магнитные поля изменяются в фазе. Во всех излучателях ДН по мощности всегда уже чем ДН по напряженности.
0. Фаза в ближней зоне 900, а в дальней зоне они совпадают. Излучение вызвано тем, что электрические и магнитные поля изменяются в фазе. Во всех излучателях ДН по мощности всегда уже чем ДН по напряженности.
Выясним, каково значение ![]() и куда направлена мощность излучения?
и куда направлена мощность излучения?
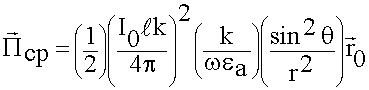
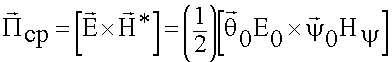 (6.3.2)
(6.3.2)
Энергия от элементарного излучателя направлена по радиусу:
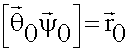
Рассчитаем мощность, отдаваемую в окружающее пространство.
Средняя мощность это поток вектора ![]() через замкнутую поверхность за период:
через замкнутую поверхность за период:
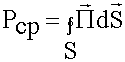 (6.3.3)
(6.3.3)
Удобнее всего выбрать в качестве поверхности сферу
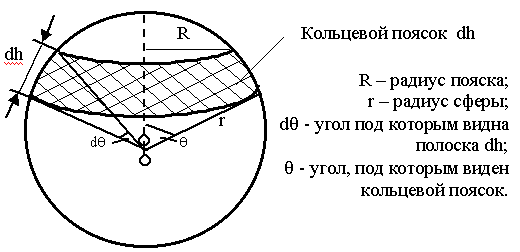
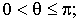 ;
; ![]()
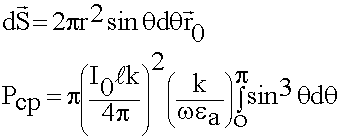
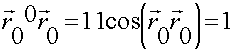
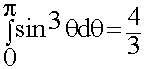 - табличный интеграл
- табличный интеграл
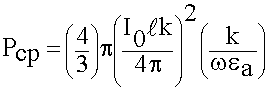 (6.3.4)
(6.3.4)
В дальнейшем будем считать, что излучатель находится в вакууме:
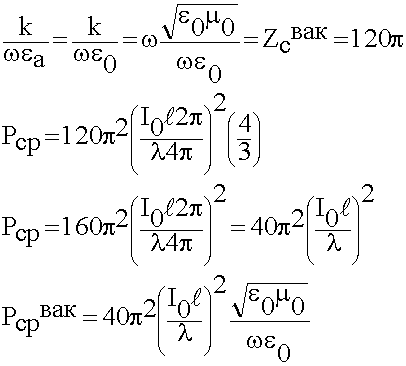 (6.3.5)
(6.3.5)
Для характеристики излучателя удобнее ввести параметр, не зависящий от тока, но характеризующий излучающие способности излучателя. В качестве такого параметра выбирают сопротивление излучения:
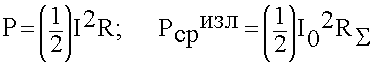
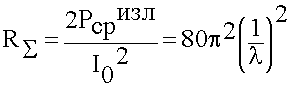 (6.3.6)
(6.3.6)
Если антенна имеет 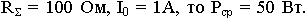 . Сопротивление излучения зависит только от размеров и для повышения излучающей способности антенны надо увеличивать ее размеры, либо повышать частоту, т.е. укорачивать
. Сопротивление излучения зависит только от размеров и для повышения излучающей способности антенны надо увеличивать ее размеры, либо повышать частоту, т.е. укорачивать  .
.
6.4. Элементарный магнитный излучатель. Принцип перестановочной двойственности
Под элементарным магнитным излучателем будем понимать замкнутый проводник с током, настолько малым, что амплитуда переменного тока во всех сечениях проводника считается неизменной.
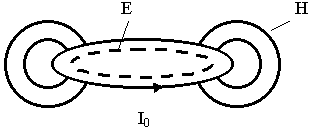
Все условия сохраняются, как и при анализе элементарного электрического излучателя.
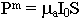
Будем использовать накопленный материал. Что общего между элементарным электрическим излучателем и магнитным? Качественно попытаемся изобразить картину поля, которую создает элементарный магнитный излучатель. Небольшая фантазия. Предположим, что имеются элементарные носители магнитных зарядов. Поскольку их на самом деле нет, то их называют фиктивными.
-
- Поле, создаваемое фиктивным зарядом
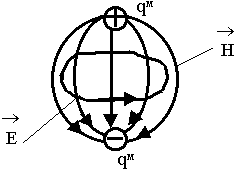
-
- Поле, создаваемое электрическим зарядом qэ
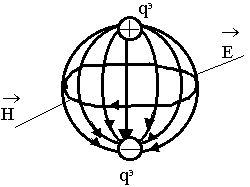
Из качественного рассмотрения картины поля видно, что структура полей, создаваемых электрическими и магнитными зарядами отличается заменой линий ![]()

Установим правила перехода от полей, создаваемыми электрическими зарядами к полям, создаваемыми магнитными зарядами. Это правило в теории поля называют принципом перестановочной двойственности.
|
Электрические источники
|
Магнитные источники
|
Из анализа уравнений
![]() (6.4.2)
(6.4.2)
Принцип перестановочной двойственности
Определим поля элементарного магнитного излучателя с помощью принципа перестановочной двойственности. Для электрического излучателя (дальняя зона):
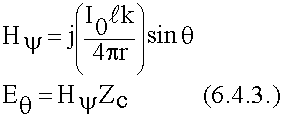
По определению:
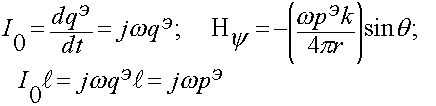
Для магнитного излучателя:
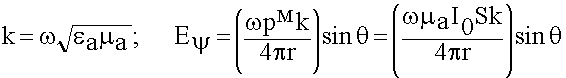
Сопротивление излучения у элементарных магнитных излучателей значительно меньше, чем у элементарных электрических излучателей. Почему?
Излучение – это токи смещения. Если система открытая, то токам легче открываться. Iпр
На практике используется комбинация штыря и витка, т.к. ориентация на “0” очень четкая (охота на лис).
Диаграмма направленности кардиоида

Максвелл в своих трудах утверждал, что окружающая среда и вакуум необходимы для существования токов смещения, так же как и проводники для токов проводимости. В конце 70-х годов прошлого столетия Гельмгольц поручает ученику Герцу провести опыты, опровергающие теорию Максвелла. Никаких приборов не было. Герц считал, что если ЭВМ отсутствуют, то эксперимент должен провалиться (а он этого хотел).
Две проволоки на некотором расстоянии друг от друга. Через некоторое время после разряда на одном из проводов Герц обнаружил искры у другой проволоки. Герц поставил экран, затем призму, пересчитал все, и оказалось то, о чем давно говорил Максвелл. Сам Герц написал о том, что надо запретить использовать его открытия для связи. Антенны для низкочастотных колебаний получались огромных размеров (испытания проводились на низких частотах). Попытаемся сделать расчеты. Изучение раздела “Излучение” начнем с понятия электродинамических потенциалов.
7. Плоские электромагнитные волны
7.1. Понятие волнового процесса
Мир, в котором мы живем, - мир волн. Чем характеризуется мир волн, волновых процессов?
Волновой процесс имеет следующие характерные признаки:
- Волновой процесс всегда переносит энергию и импульсы. Нас интересуют волновые процессы ЭМВ.
- Конечная скорость всех волновых процессов. В случае ЭМВ - это скорость света.
- Независимость волновых процессов друг от друга. В этой комнате существуют поля самых разных частот, поля р/станций, света и т.д.
- Волновые процессы, различные по физической природе, описываются одним и тем же математическим аппаратом.
Под волновым процессом понимают возмущение некоторой величины в пространстве, перемещающееся с конечной скоростью, переносящее мощность без переноса вещества.
7.2. Плоская ЭМВ в идеальной среде
Под плоской ЭМ волной понимают волновой процесс, у которого составляющие электрического и магнитного полей изменяются в одинаковой фазе в плоскости перпендикулярной направлению распространения.
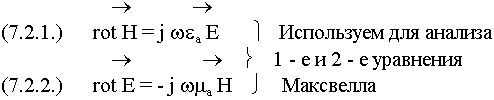
Источники, создающие плоские волны не входят в эти уравнения. Мы рассматриваем волновые процессы в дальней зоне, т.е. в пространстве за пределами зарядов и токов. Решим уравнения относительно Е и Н.
Из уравнения (7.2.1.) выразим Е и подставим в (7.2.2.):
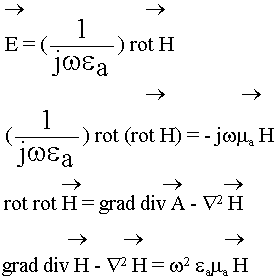
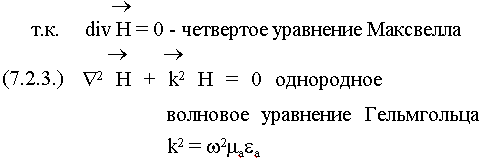
Точно так же из второго уравнения получаем уравнения для вектора Е:
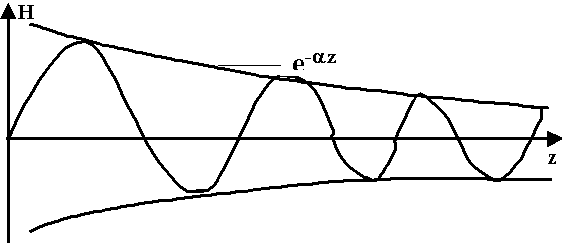
В развернутом виде запишем уравнения:
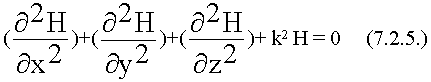
Решать такое уравнение трудно. Предположим, что источник ЭМ колебаний находится очень далеко от той области, где рассматриваем волны.
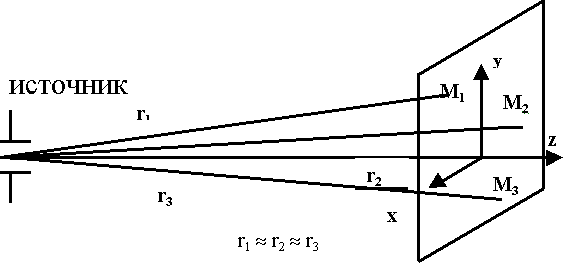
т.к. источник очень далеко, то расстояния до точек можно считать одинаковым. Из физического смысла задачи, можно утверждать, что изменения полей по координате y, х нет, т.е.:
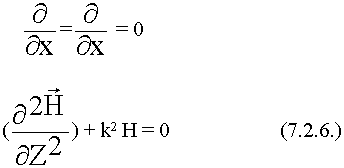
Для плоской ЭМВ волновое уравнение упрощается. Решение уравнения:
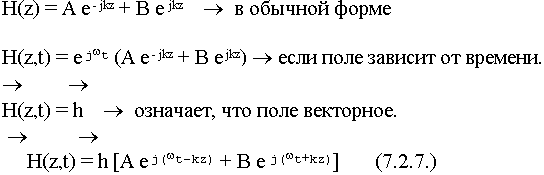
Выделим составляющую поля c амплитудой А:

Выделим из комплексного выражения действительную часть:
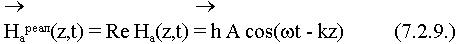
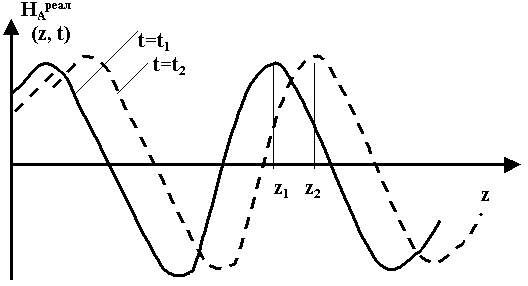
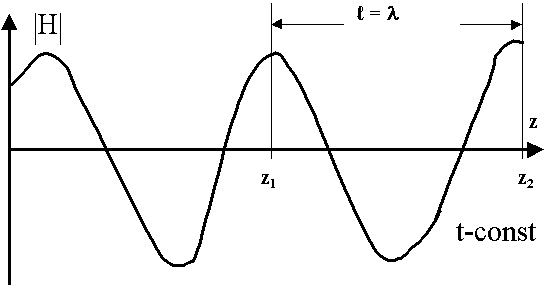
Фотография процесса в момент времени t = t1, t = t2. С какой скоростью перемещается фронт с одинаковой фазой? Выясним это:
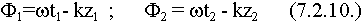
Прибор регистрирует одинаковую напряженность, надо потребовать, чтобы Ф1 = Ф2
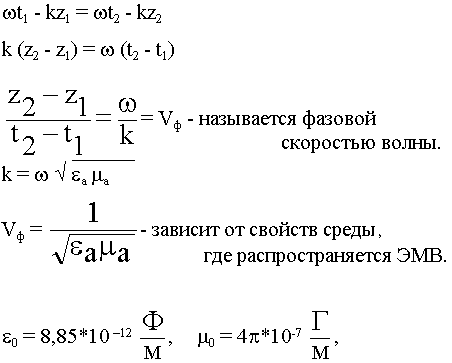
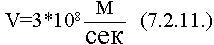
 - называют пространственную периодичность волнового процесса.
- называют пространственную периодичность волнового процесса.
 - это длина пути, которую проходит фронт с одинаковой фазой за период, или - это есть расстояние, которое проходит фазовый фронт за 1 период.
- это длина пути, которую проходит фронт с одинаковой фазой за период, или - это есть расстояние, которое проходит фазовый фронт за 1 период.
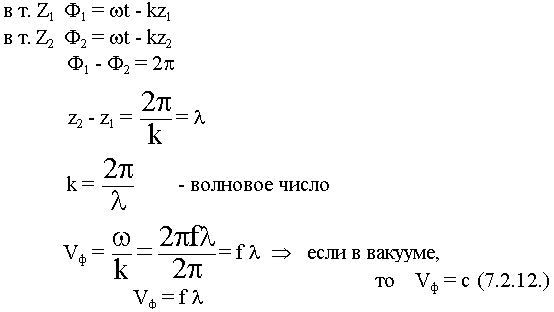
Выясним связь напряженностей Е и Н в ЭМВ:
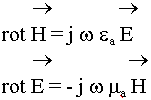
Спроектируем уравнение на оси координат:
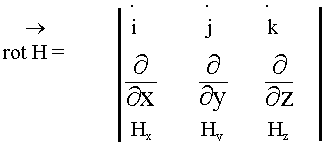
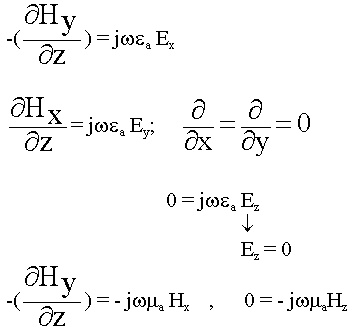
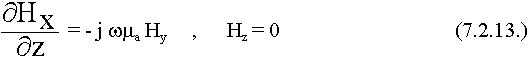
В ЭМВ отличны от нуля только две составляющие в плоскости 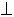 плоскости распространения:
плоскости распространения:
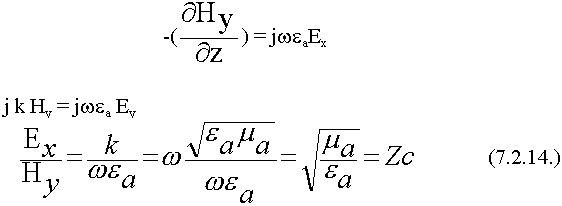
Это лишний раз подчеркивает, что сферические волны излучателя в дальней зоне превращаются в плоские ЭМВ.
Ориентация векторов  и
и  .
.
Для плоской ЭМВ  всегда
всегда 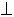
 .
.
Покажем, что величина 
 = 0:
= 0:

Поскольку в рассматриваемой задаче рассматривается только один источник, то учитываем только волну с амплитудой А. В пространстве имеются 2 взаимно перпендикулярных поля (  и
и  ). Как определить направление переноса энергии?
). Как определить направление переноса энергии?
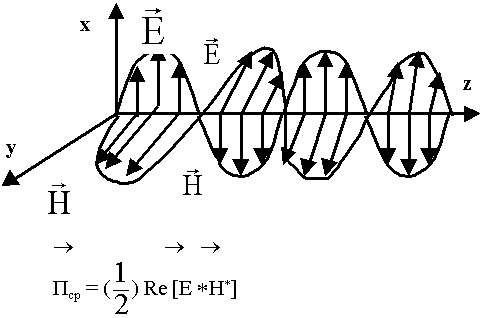
Итоги:
- Составляющие
 и
и  лежат в плоскости перпендикулярной направлению распространения и изменяются в фазе (там где max Е там max Н, и наоборот)
лежат в плоскости перпендикулярной направлению распространения и изменяются в фазе (там где max Е там max Н, и наоборот)
- Отношение
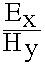 = Zc определенная величина в случае вакуума Zc = 120
= Zc определенная величина в случае вакуума Zc = 120  . Плоская ЭМВ однородная.
. Плоская ЭМВ однородная. - Амплитуды Е и Н не зависят от поперечных координат.
- У плоской ЭМВ Ez = 0 , Hz = 0.
7.3. Плоские волны в реальных средах
Предыдущий анализ относился к идеальным средам. В реальных средах часть энергии будет теряться в среде, значит амплитуда волны будет убывать. Любая реальная среда - набор связанных зарядов (диполей), могут быть и свободные заряды.
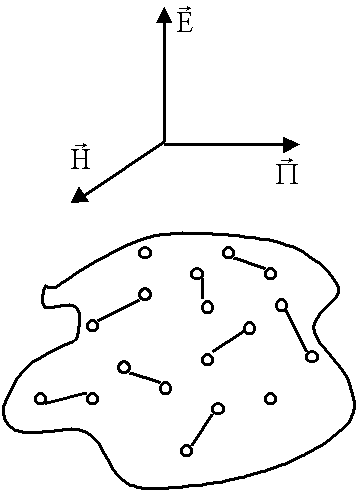
Часть энергии переходит в тепло. Количественно опишем процесс.
В реальных средах, при гармонических воздействиях проницаемости величины комплексные:
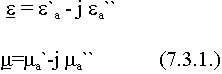
Все рассуждения и результаты сохраняют силы, но параметры 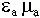 - комплексные.
- комплексные.
Амплитудные соотношения.
С этой целью рассмотрим, что представляет собой волновое число в реальной среде:
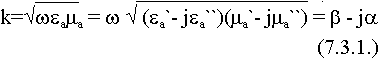
поскольку величины 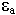 и
и 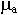 - комплексные, то k - тоже величина комплексная. К каким последствиям это может привести? Рассмотрим волновой процесс:
- комплексные, то k - тоже величина комплексная. К каким последствиям это может привести? Рассмотрим волновой процесс:
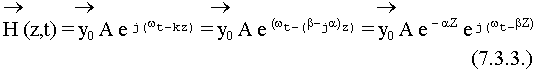

Параметр  получил название коэффициента затухания.
получил название коэффициента затухания. 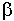 - фазовая постоянная - вещественная часть волнового числа.
- фазовая постоянная - вещественная часть волнового числа.
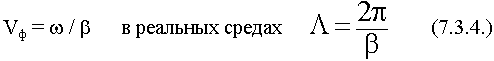
Понятие 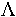 было введено для идеального диэлектрика. Если затухание мало, то можно выбрать точки, где поля отличаются по фазе на 2
было введено для идеального диэлектрика. Если затухание мало, то можно выбрать точки, где поля отличаются по фазе на 2 и считать, что это
и считать, что это 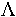 . Если затухание очень велико, периодичность процесса теряет смысл (соленая вода), понятием
. Если затухание очень велико, периодичность процесса теряет смысл (соленая вода), понятием  можно пользоваться условно.
можно пользоваться условно.
Количественная оценка.
Рассмотрим поведение амплитуды в точках:
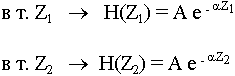
Изменение
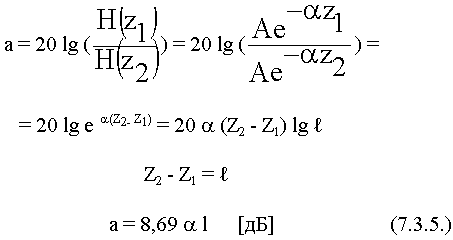
во столько раз, пересчитанных в дБ уменьшилась амплитуда поля .
Под глубиной проникновения поля понимают расстояние, на котором амплитуда поля убывает в е раз
(вектор  и
и  ).
).
Изменение поля 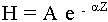 . На расстоянии равном глубине проникновения в точке Z = 0, Н1 = А
. На расстоянии равном глубине проникновения в точке Z = 0, Н1 = А
в т. 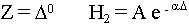
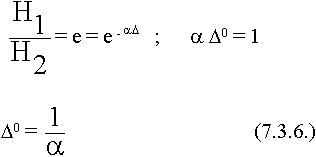
Фазовые соотношения
Воспользуемся понятием “характеристическое сопротивление cреды”
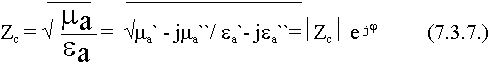
в реальных средах Zc величина комплексная. Поведение  и
и  в реальной среде:
в реальной среде:
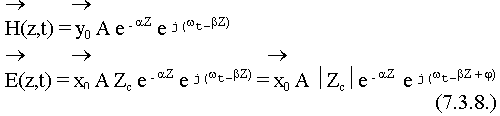
Модуль характеристического сопротивления означает отношение амплитуд между электрическим и магнитным полями, а фаза характеристического сопротивления показывает величину сдвига фаз между  и
и  . В реальных средах всегда
. В реальных средах всегда  и
и  сдвинуты на некоторую величину.
сдвинуты на некоторую величину.
Волновой процесс в реальных средах
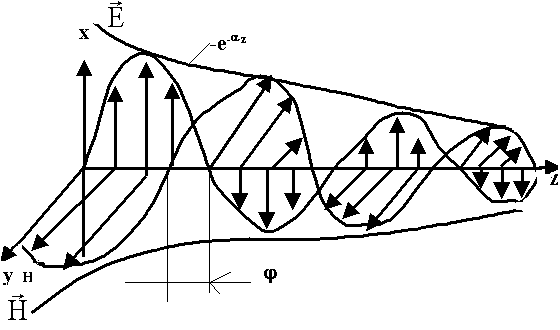
Расчет коэффициента затухания и фазовой постоянной в реальной среде
Проведем расчет для частного случая, широко используемого на практике.
Реальная cреда немагнитный диэлектрик.
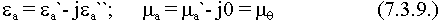
(почва, вода)
Порядок расчета:
1) Из общих выражений для k:
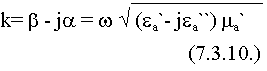
Выделим вещественную и мнимую часть. Для этого левую и правую часть возведем в квадрат, т.к. надо избавиться от радикалов:
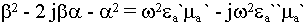
Два комплексных числа тогда равны, когда равны и вещественные и мнимые части.
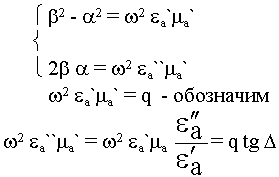
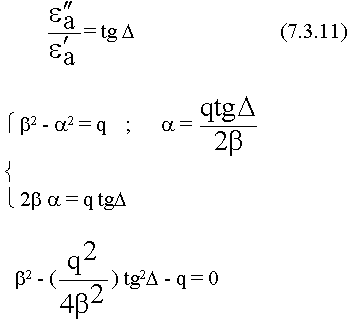
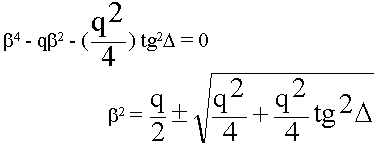
Какой знак взять + или - ?
Исходя из физического смысла оставляем только +, т.к. 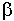 - будет отрицательная.
- будет отрицательная.
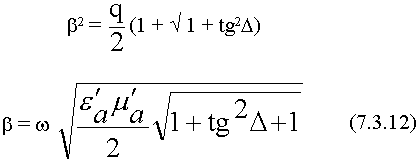
для  решение аналогичное:
решение аналогичное:
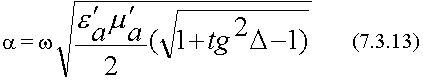
Выводы:
1. По определению 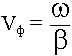
Vф = 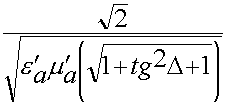
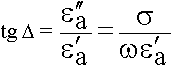
Vф зависит от частоты. Встретились с явлением дисперсии. Зависимость Vф от f называется дисперсией. Идеальная среда не обладает дисперсией.
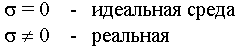
Рассмотрим поведение ЭМВ в двух случаях:
1) Среда с малыми потерями, малым затуханием:
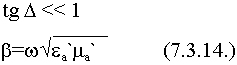
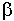 совпадает с волновым числом для идеального диэлектрика с параметрами
совпадает с волновым числом для идеального диэлектрика с параметрами 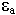 ,
, 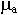 .
.
Для  :
:
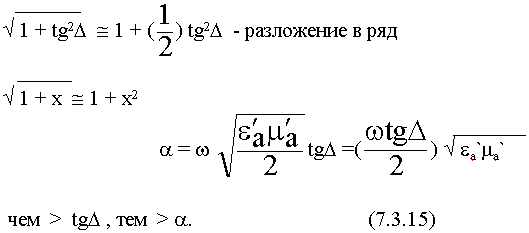
2) Среда с большими потерями.
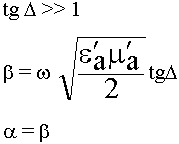
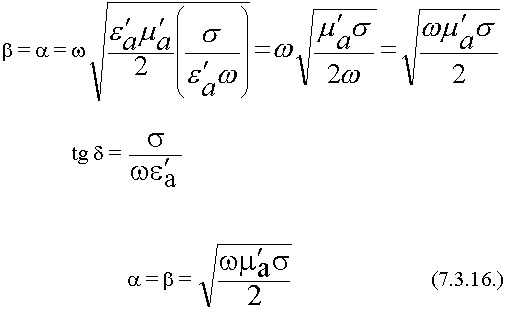
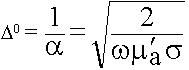
Пример:
Определить во сколько раз уменьшается амплитуда волны на расстоянии равном длине волны (в среде с большими потерями).
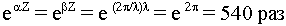
7.4. Групповая скорость плоских волн
Все реальные сообщения занимают определенный спектр частот и возникает вопрос, какой реальный сигнал передается?
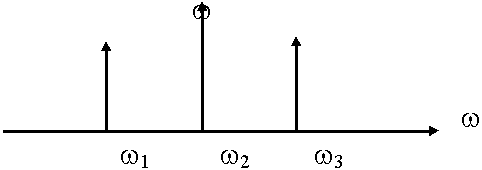
В реальных средах, каждая гармоническая составляющая передается со своей скоростью w 1 w 2 w 3. С какой скоростью передается сигнал?
Рассмотрим простой случай, когда сообщение состоит из двух гармонических сигналов:
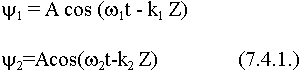
Рассмотрим сложение двух сигналов:
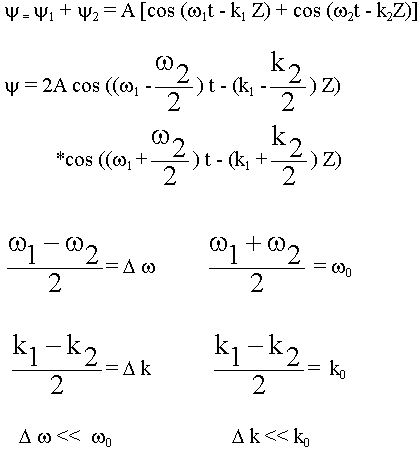

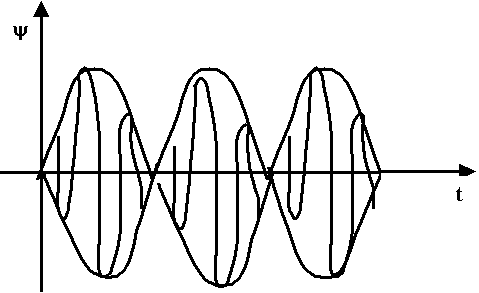
При оценке скорости реальных сигналов, специалисты рассматривают скорость переноса max энергии. Рассмотрим с какой скоростью изменяется в пространстве фронт max амплитуд.
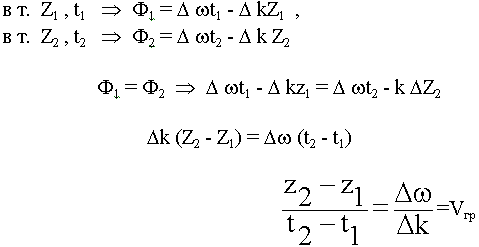
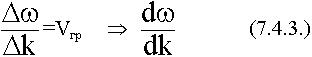
Vгр по физическому смыслу характеризует скорость перемещения огибающей сигнала. С движением огибающей связано перемещение энергии, поэтому с групповой скоростью связано перемещение энергии:

Vф связана с изменением состояния, а не с переносом энергии.
Vф - скорость изменения состояния фазового фронта.
Пример: Лампочки последовательно загораются, изменение скорости состояния загорания может сколько угодно большой.
7.5. Поляризация плоских электромагнитных волн
Под поляризацией будем понимать заданную в пространстве ориентацию вектора  или
или  . Различают 3 вида поляризации: линейную (вектор Е и Н ориентирован всегда вдоль одной линии прямой), круговую поляризация (вектор
. Различают 3 вида поляризации: линейную (вектор Е и Н ориентирован всегда вдоль одной линии прямой), круговую поляризация (вектор  или
или  вращается по кругу), эллиптическую поляризация (вектор Е или Н вращается по эллипсу).
вращается по кругу), эллиптическую поляризация (вектор Е или Н вращается по эллипсу).
Возьмем два ортогональных колебания:
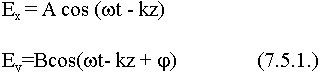
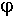 - показывает сдвиг во времени, они не совпадают по фазе.
- показывает сдвиг во времени, они не совпадают по фазе.
Что получится в результате сложения двух ортогональных колебаний?
1) А 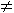 В амплитуды разные, а сдвиг фаз равен 0.
В амплитуды разные, а сдвиг фаз равен 0.
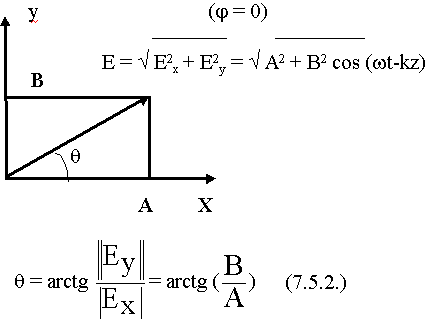
Сложение двух ортогональных линейно- поляризованных колебаний, изменяющихся в одной фазе, но с разной амплитудой дает линейно- поляризованное колебание ориентированное под некоторым углом.
2) 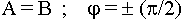
Два ортогональных колебания по определению:
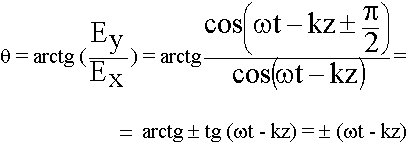
Сложение двух ортогональных линейно - поляризованных колебаний изменяющихся с одинаковой амплитудой и фазой со сдвигом  дает вращающее колебание (колебание с круговой поляризацией).
дает вращающее колебание (колебание с круговой поляризацией).
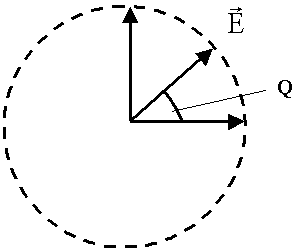
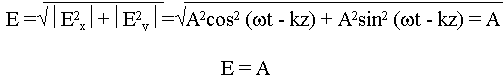
Направление вращения определяется опережением или отставанием по фазе.
3) В общем случае, когда А 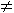 В, и фазы разные, вектор
В, и фазы разные, вектор  или
или  вращается по эллипсу.
вращается по эллипсу.
Любую волну с линейной поляризацией можно представить в виде двух волн с круговой поляризацией, имеющих разное направление.
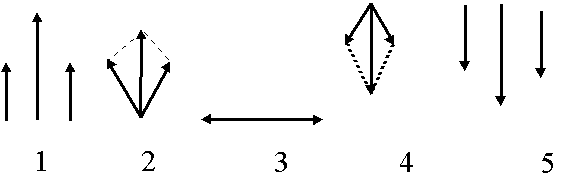
Явление поляризации широко используется на практике. Все приемные устройства: служебная связь - вертикальная поляризация, в России прием ТВ на горизонтальную поляризацию, вертикальная поляризация - режим передачи, горизонтальная - режим приема. Круговая поляризация широко используется в радиолокации.
8. Плоские ЭМВ на границе раздела двух сред. Волны в неоднородных средах
8.1. Необходимость рассмотрения граничных условий
В реальной жизни неизбежно появляются препятствия на пути распространения ЭМВ. Что же происходит при этом ?
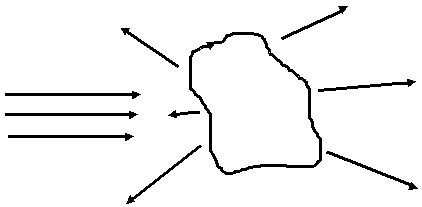
В этом случае задача чрезвычайно сложная. В частном случае еще можно. Для ЭМВ также как и для оптических имеет место рассеяннее, дифракция. В качестве препятствия рассмотрим случай простейший (бесконечно большое препятствие).
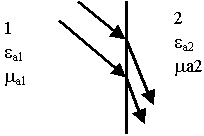
Уравнения Максвелла дают информацию о поведении полей с непрерывным изменением проницаемости:
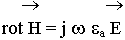
1) Уравнения Максвелла из-за разрыва проницаемостей нельзя применять к точкам, лежащим на границе раздела. Информацию о поведении полей на границе мы будем получать из дополнительных условий, их называют граничными условиями.
2) Решение уравнений Максвелла всегда записывается с точностью до const, чтобы const эту получить надо знать дополнительные условия. В качестве таких условий используют граничные условия. При формировании граничных условий удобно любой вектор разлагать на составляющие.
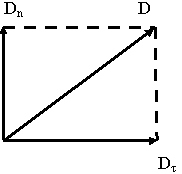
В дальнейшим для поля произвольно ориентированного к границе раздела будем выделять нормальную и касательную составляющие. Граничные условия отдельно записываются для нормальных и касательных составляющих.
8.2. Граничные условия для нормальных составляющих векторов электрического поля
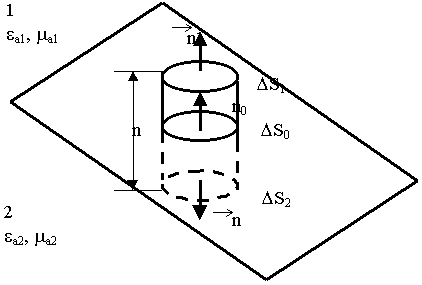
Для выяснения граничных условий используем интегральное соотношение. Выделим площадку небольших размеров. Формируем замкнутую поверхность (цилиндрическую). Применим к этой поверхности т. Гаусса:
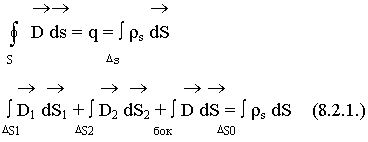
Предположим, что размеры площадок равны и достаточно малы, что в пределах этих площадок вектор D не меняется:
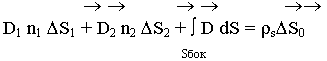
Осуществляем предельный переход, когда:
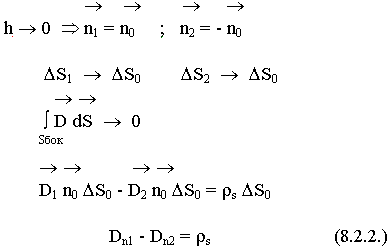
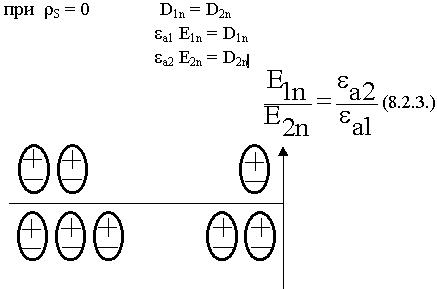
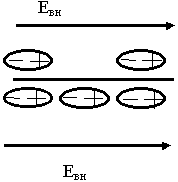
На границе раздела нормальные составляющие терпят разрыв (изменяются скачком) на величину 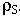 . Почему происходит скачок, с физической точки зрения ? Предположим на каждую из сред действуют силы Евн. Каждая среда имеет диполи. Эти диполи под воздействием поля будут ориентироваться. На границе раздела появились нескомпенсированные положительные заряды, которые создают поле свое.
. Почему происходит скачок, с физической точки зрения ? Предположим на каждую из сред действуют силы Евн. Каждая среда имеет диполи. Эти диполи под воздействием поля будут ориентироваться. На границе раздела появились нескомпенсированные положительные заряды, которые создают поле свое.
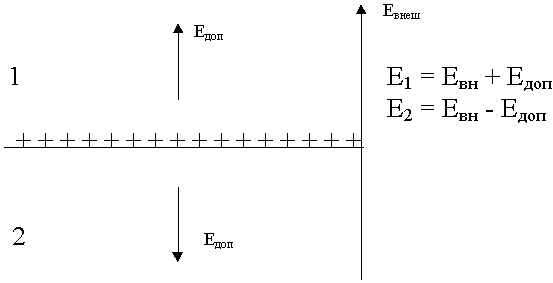
Граничные условия для касательных составляющих векторов электрического поля
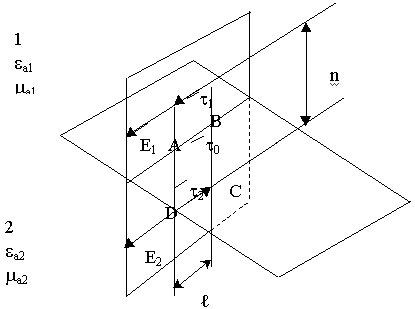
В плоскости Р построим контур, часть которого находится в нижней среде, часть в верхней. К контуру АBCD применим закон электромагнитной индукции:
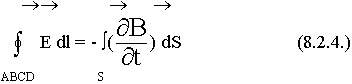
Условие: 1) направление обхода контура.
2) ориентация касательных векторов.
1. Левую часть при вычислении интеграла разобьем на части:
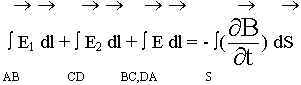
размеры контура малы, значение поля в пределах контура не меняются:
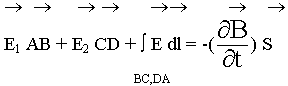
2. Стягиваем контур, устремим высоту контура к 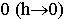
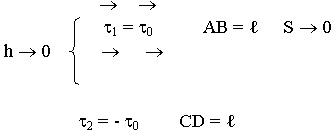
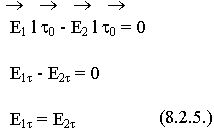
Касательные составляющие вектора Е непрерывны при переходе через границу раздела.
1. Результирующий заряд на границе равен 0 (граница не заряжена).
Рассмотрим границу раздела, состоящую из двух сред. Пусть поле (во второй среде) приложено параллельно границе в первой среде тоже параллельно.
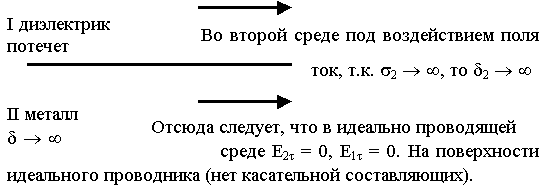
На поверхности идеального проводника есть только нормальные составляющие:
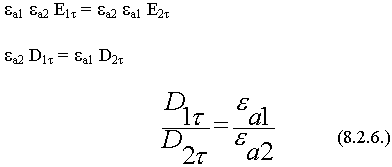
Касательные составляющие вектора D изменяются скачком.
Граничные условия для нормальных составляющих векторов магнитного поля.
Картинка такая же, как для нормальных составляющих электрического поля.
Применяем к поверхности теорему Гаусса для магнитного поля.

Нормальные составляющие вектора В непрерывны на границе раздела.
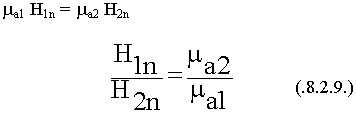
Нормальные составляющие вектора Н изменяются скачком
при переходе через границу на величину 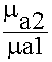
Граничные условия для касательных составляющих магнитного поля.
Построение рис. совпадает со случаем для касательных составляющих вектора Е. Применяя к контуру ABCD закон полного тока (при Iпол = 0) имеем:
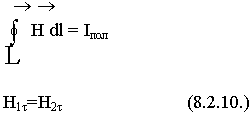
Касательные составляющие вектора Н непрерывны:
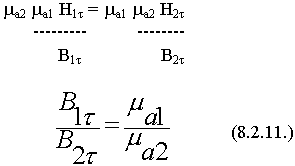
Касательные составляющие вектора В при переходе через границу изменяется скачком на величину 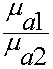 . Физическое объяснение вытекает из свойств сред.
. Физическое объяснение вытекает из свойств сред.
8.3. Нормальное падение плоской волны на плоскую границу раздела
Предположим, что имеется граница раздела (бесконечно плоская граница). На эту границу падает волна.
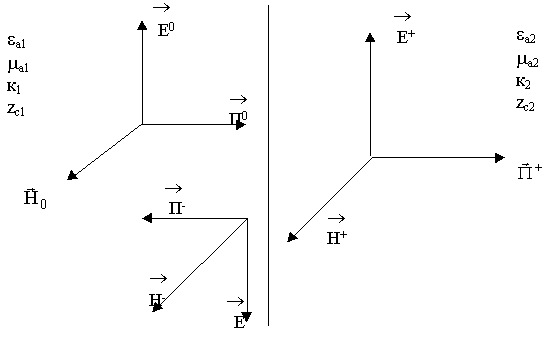
Часть волны будет отражаться, часть пройдет во вторую среду. Для отраженной волны один из векторов, либо вектор Е либо Н, должен изменить направление. Какой ? Пока еще не можем сказать какой. Ответ будет чуть позже. Анализ:
1. Запишем исходные составляющие полей в каждой среде в общем виде:

во второй среде
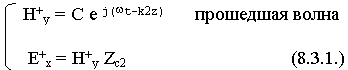
Как определить амплитуды А, В, С ? Считаем, что на границу падает волна с известной амплитудой А. Чтобы определить неизвестные амплитуды, воспользуемся граничными условиями. Для данной задачи используем граничные условия для касательных составляющих магнитных полей 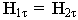 , для электрических полей
, для электрических полей 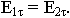
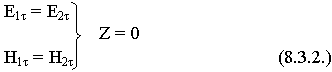
В первой среде суммарные электрическое и магнитное поля (падающие и отраженные волны).
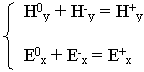
При переходе через границу раздела координатная составляющая е jkz исчезает, т.к.
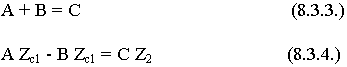
Коэффициент отражения R определяют как отношение амплитуды отраженной волны электрического поля к амплитуде падающей волны электрического поля. Можно и для магнитного поля, это непринципиально, изменится только знак:
R = 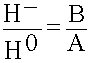
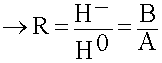
Коэффициент прохождения Т определяют как отношение амплитуды прошедшей волны к амплитуде падающей волны:
Т = 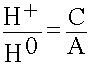 разделим (8.3.3) на А. (8.3.5.)
разделим (8.3.3) на А. (8.3.5.)
(8.3.4.) разделим на ZcА:
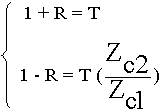
Сложим:
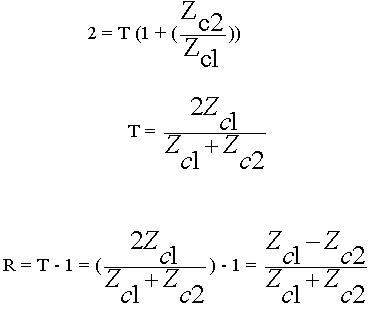
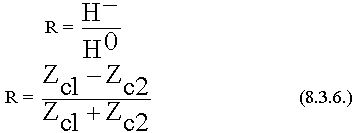
Анализ полных выражений
Мы установили, что коэффициент отражения зависит только от свойств cреды:
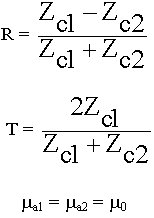
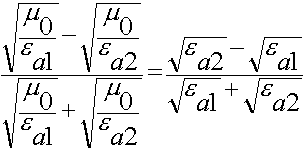
Выводы:
- Отражение волн происходит от оптически более плотной среды
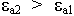 . У отраженной волны ориентация вектора Е изменяется на 1800.
. У отраженной волны ориентация вектора Е изменяется на 1800. - Отражение от оптически менее плотной среды вода/воздух
 . Вектор Е сохраняет свою ориентацию в отраженной волне, у отраженной волны будет изменяться вектор Н на 1800.
. Вектор Е сохраняет свою ориентацию в отраженной волне, у отраженной волны будет изменяться вектор Н на 1800. - Режим согласования сред. Всегда режиму согласованных сред соответствует требование, что отраженной волны нет.
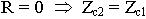
- Режим полного отражения.
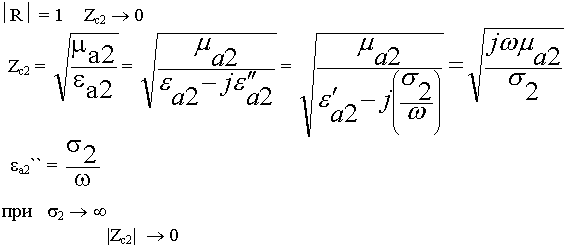
Полное отражение можно получить от границы раздела с большой проводимостью. Выясним особенности распределения ЭМП в первой среде. Результирующее поле является суммой двух волн:
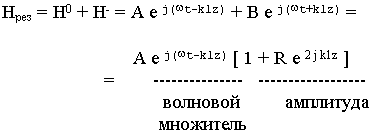
Амплитуда в результирующем поле зависит от координаты Z.
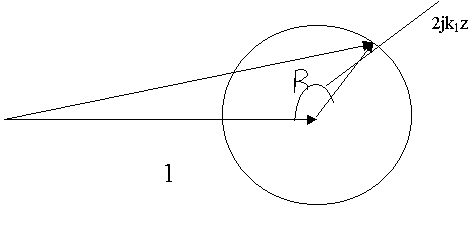
Воспользуемся методом векторного сложения:
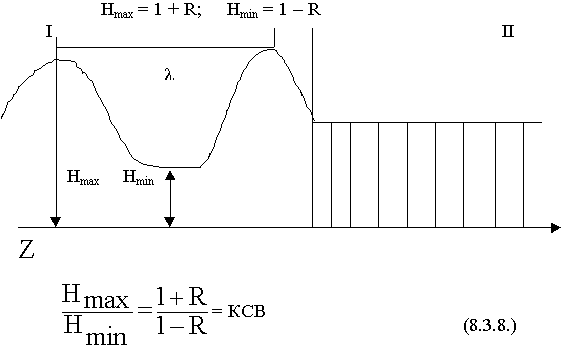
В линиях передачи протекают точно такие же физические процессы по таким же закономерностям. Выясним чему равно расстояние между соседними пучностями поля.
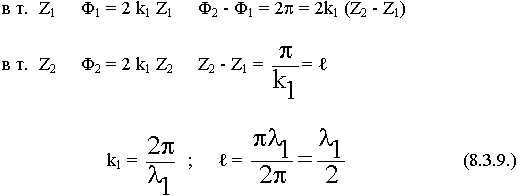
Вывод: измеряя расстояние между двумя узлами и удвоив его, получим длину волны.
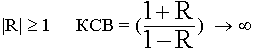
8.4. Наклонное падение волны на плоскую границу раздела двух сред
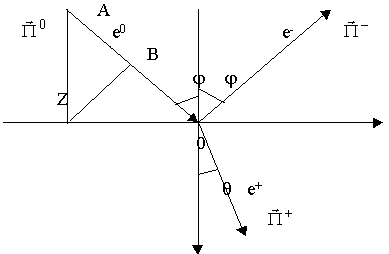
Выясним угловые соотношения при наклонном падении:
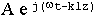 - направление распространения волны совпадает с осью Z.
- направление распространения волны совпадает с осью Z.
Отсчет пути проходимого волной проводится в направлении движения волны:
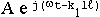 - для падающей волны.
- для падающей волны.
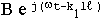 - для отраженной волны.
- для отраженной волны.
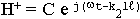 - прошедшая волна.
- прошедшая волна.
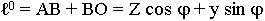
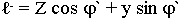
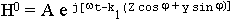
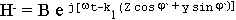

Воспользуемся граничными условиями задачи для касательных составляющих полей:
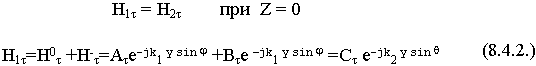
А, В, С - произвольные амплитуды.
Это условие должно выполняться при любом значении у, т.е. показатели всех экспонент должны быть равны. Из этого автоматически следует:

Для идеальной среды проницаемости являются const и тогда второй закон Снеллиуса не зависит от частоты.
Выводы:
- Законы Снеллиуса не зависят от поляризации падающей волны.
- Первый закон Снеллиуса справедлив для любых частот.
Второй закон:
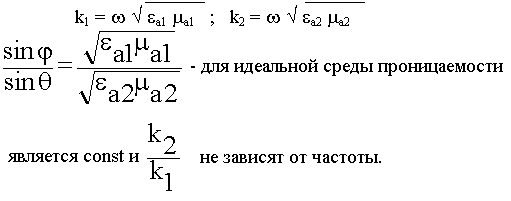
Если среда реальная:
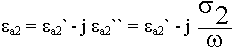
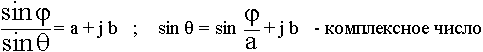
Для сред с потерями геометрическое толкование второго закона Снеллиуса теряет смысл.
Амплитудные соотношения при наклонном падении. Формулы Френеля.
Амплитуды отраженных и прошедших волн зависят от поляризации падающих волн. Будем различать 2 вида поляризации:
- Горизонтальная поляризация падающей волны.
Вектор  параллелен границе раздела двух сред.
параллелен границе раздела двух сред.
- Вертикальная поляризация падающей волны. Вектор
 параллелен границе раздела двух сред.
параллелен границе раздела двух сред.
Горизонтальная поляризация падающей волны.
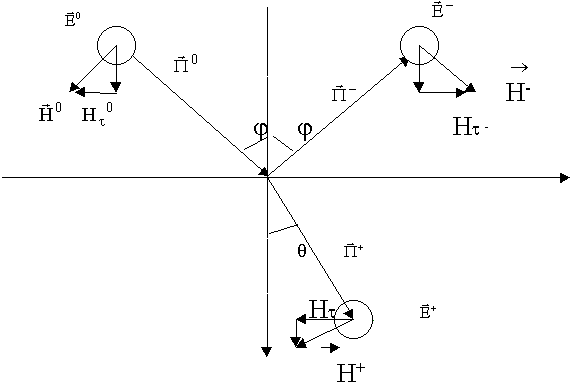
Чтобы определить амплитуды, потребуем выполнения граничных условий. Поскольку Е параллелен границе раздела, потребуем выполнения граничных условий по касательным составляющим:
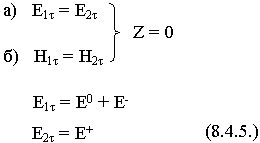
Выделим в магнитном поле касательные составляющие:
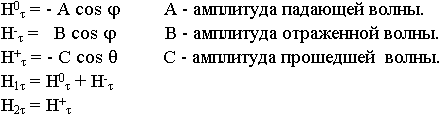
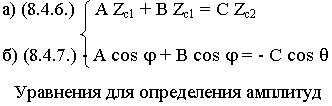
Введем понятие коэффициента отражения в случае горизонтальной поляризации, лучше через электрические поля, т.к. вектор  не меняет ориентации.
не меняет ориентации.
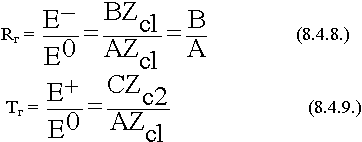
Тг - коэффициент прохождения.
Разделим на A Zc1 уравнение (8.4.6.), а на A cos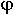 ; уравнение (8.4.7.):
; уравнение (8.4.7.):
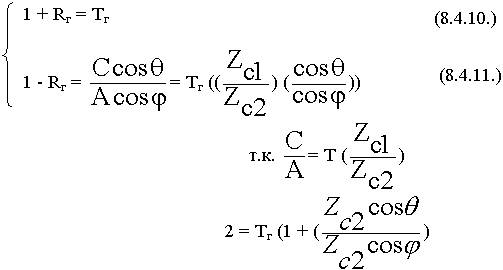
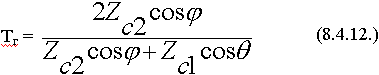
Из уравнения (8.4.10.) определяем:
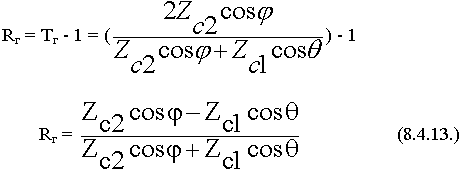
Формулы Френеля для горизонтальной поляризации.
Вертикальная поляризация.
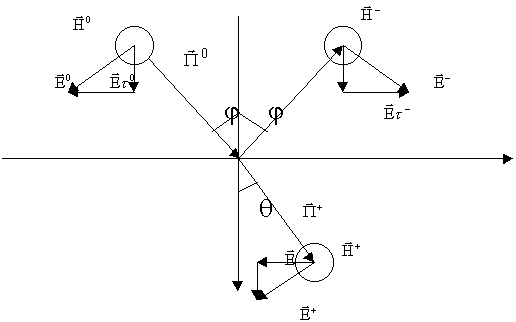
Воспользуемся принципом перестановочной двойственности (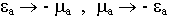 ):
):
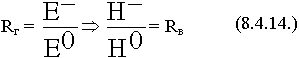
Вектор  не меняет ориентацию, удобно через Н.
не меняет ориентацию, удобно через Н.
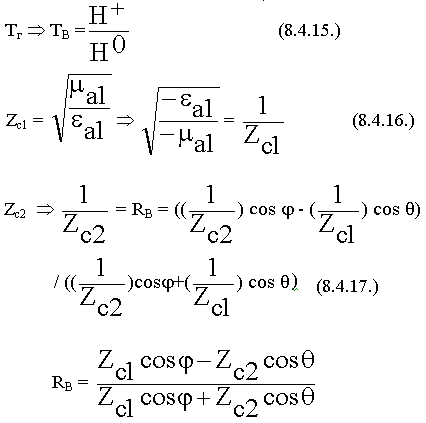
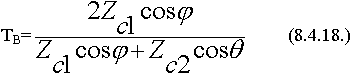
Может ли в случае наклонного падения вся волна проходить во вторую среду без отражения?
8.5. Согласование при наклонном падении. Угол Брюстера
Условие согласования при наклонном падении соответствует требованию, чтобы 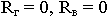
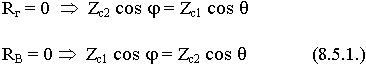
Видно, что условие согласования зависит от угловых соотношений и от свойств среды.
Качественно:
1) При распространении волны в немагнитном диэлектрике.
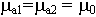 для волны с горизонтальной поляризацией режим согласования никогда не подобрать, т.е. нет такого угла
для волны с горизонтальной поляризацией режим согласования никогда не подобрать, т.е. нет такого угла 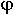 , при котором условие бы это выполнялось.
, при котором условие бы это выполнялось.
Качественно. Под воздействием приложенного поля диполи будут ориентироваться по полю. Такие диполи излучают перпендикулярно своей оси, часть энергии вверх, часть вниз (прошедшая волна).
2) для волны с вертикальной поляризацией можно подобрать такой угол, при котором вся волна перейдет во вторую среду, т.к. параллельно своей оси диполь не излучает.
1)
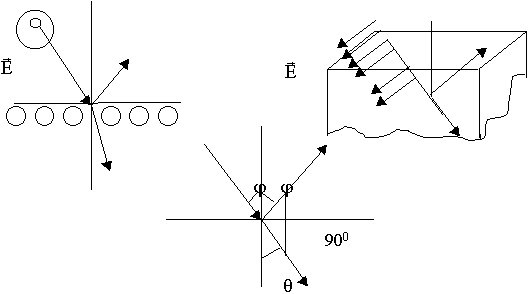
Из анализа - направление диполя параллельно отраженной волне. 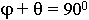
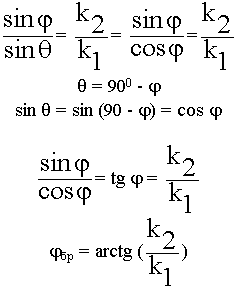
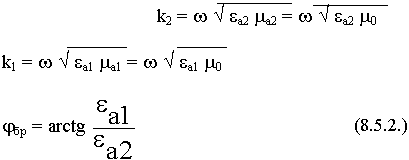
В случае немагнитных диэлектриков режим согласования при наклонном падении выполняется в случае вертикальной поляризации.
8.6. Полное внутреннее отражение
Выясним, при каких условиях имеет место полное отражение волны от границы раздела при наклонном падении.
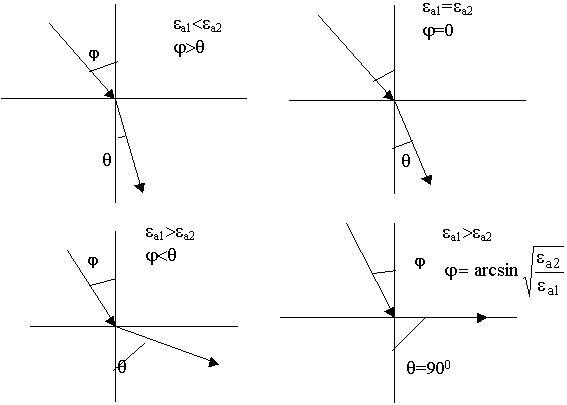
Угол 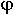 , при котором прошедшая волна идет вдоль границы раздела получил название - угол полного внутреннего отражения, а явление распространения называется полным внутренним отражением. Явление полного внутреннего отражения реализуется, когда волна распространяется из более плотной cреды в менее плотную.
, при котором прошедшая волна идет вдоль границы раздела получил название - угол полного внутреннего отражения, а явление распространения называется полным внутренним отражением. Явление полного внутреннего отражения реализуется, когда волна распространяется из более плотной cреды в менее плотную.
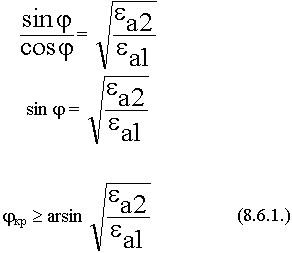
Отражение происходит от границы раздела двух диэлектриков, металл не требуется, подобраны углы и параметры сред.
Для явления полного внутреннего отражения характерно:
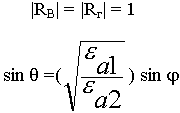
можно сделать 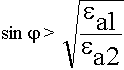 тогда sin
тогда sin 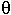 > 1 ? Неясно, что такое
> 1 ? Неясно, что такое 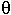 , когда sin
, когда sin 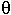 > 1.
> 1.
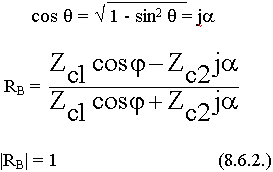
Условию полного внутреннего отражения соответствует полное отражение волны от границы раздела аналогично | Rг| = 1.
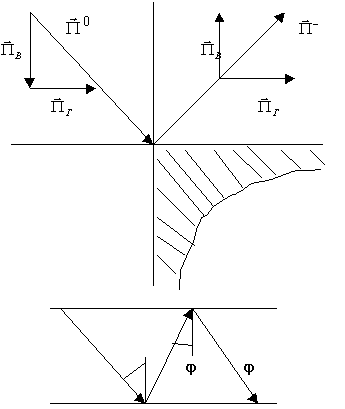
При выполнении режима полного внутреннего отражения энергия волны распространяется вдоль границы (поверхности) раздела, а во второй среде экспоненциально убывает. Волну называют поверхностной. Подошли к таким линиям как световод, к этому вернемся позже.
8.7. Поверхностный эффект при наклонном падении
Поверхностный эффект проявляется в резком изменении амплитуды поля вблизи границы раздела сред, при этом одна из сред обладает большой
проводимостью (на поверхность металла, влажную почву, морскую воду). Предположим, что плоская ЭМВ с произвольной поляризацией падает на хорошо проводящую поверхность.

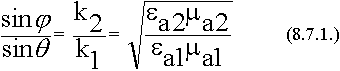
При достаточно большом значении 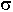 среды, прошедшая во вторую среду волна будет распространяться по нормали (
среды, прошедшая во вторую среду волна будет распространяться по нормали ( очень мал).
очень мал).
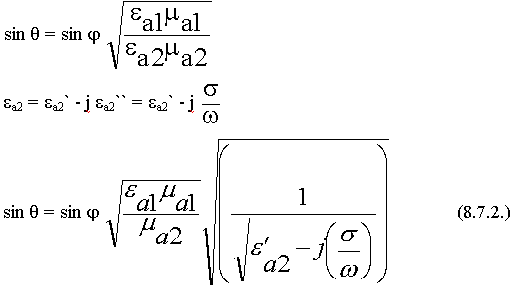
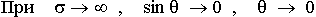
Амплитуда поля уменьшается очень быстро, т.к. 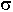 велика,
велика, 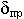 - тоже очень сильно убывает.
- тоже очень сильно убывает. 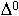 – глубина проникновения. Это расстояние, на котором амплитуда поля убывает в е раз.
– глубина проникновения. Это расстояние, на котором амплитуда поля убывает в е раз.
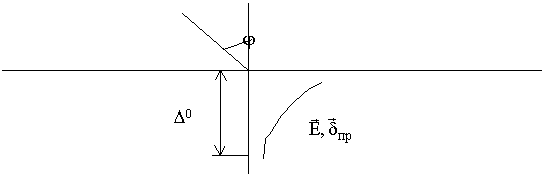
Можно обобщить это и на металлический проводник. Поверхностный эффект проявляется в проводнике. Центральную часть можно убрать, т.к. ток протекает в тонком слое (при постоянном токе, он распределяется по сечению). Поверхностный эффект приводит к увеличению сопротивления провода и уменьшению индуктивности.
Неприятности. В тонком поверхностном слое сильная плотность тока, сильный разогрев.
9. Направляемые электромагнитные волны. Направляющие системы
Под направляющей системой понимают устройство, ограниченное в двух измерениях и осуществляющее передачу ЭМ энергии в третьем измерении. Волны, которые распространяются в таких направляющих системах получили название - направляемые электромагнитные волны. Такие направляющие системы называются волноводами.
9.1. Недостатки обычных линий передачи преимущества волноводов
Широкое развитие получили двухпроводные и коаксиальные линии еще в прошлом веке.

Недостатки: В 2-х проводных и коаксиальных линиях резко возрастает затухание энергии с ростом частоты. Факторы:
- Поверхностный эффект в проводниках приводит к росту потерь с ростом частоты
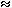 f 1/2.
f 1/2. - Диэлектрические потери. С ростом f диэлектрические потери увеличиваются пропорционально f
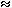 f.
f. - Излучение. В 2-х проводной линии эффект излучения очень значителен мощность излучения пропорционально квадрату f ~ f2.
В двухпроводных линиях при 
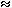 1 м и короче потери такие больше, что ее нецелесообразно применять; на
1 м и короче потери такие больше, что ее нецелесообразно применять; на  ген = 3 м, затухание в коаксиальном кабеле в среднем 0,2 дБ/м
ген = 3 м, затухание в коаксиальном кабеле в среднем 0,2 дБ/м  ген = 10 см затухание
ген = 10 см затухание 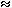 2 дБ/м, т.е. ничего не дойдет от передатчика к антенне.
2 дБ/м, т.е. ничего не дойдет от передатчика к антенне.
Из двухпроводной линии можно сделать волновод, но так не делают на практике, только на бумаге, как в детском конструкторе. Входное сопротивление отрезка длиной ![]() имеет бесконечно большое значение:
имеет бесконечно большое значение:
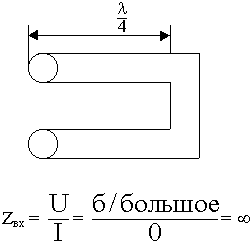
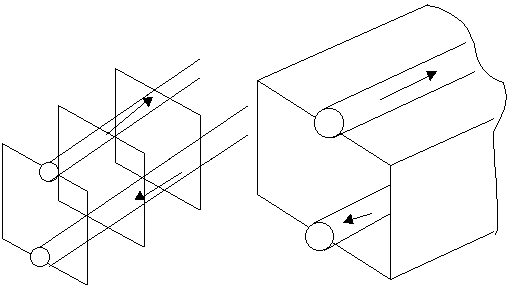
Если подключить отрезок ![]() к линии, то он никак не повлияет, т.к.
к линии, то он никак не повлияет, т.к. 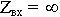 . И так сколько угодно можно подключить таких отрезков. Получили волновод.
. И так сколько угодно можно подключить таких отрезков. Получили волновод.
Достоинства:
- Трубка жесткая. Простая конструкция.
- Фактор диэлектрических потерь исключается.
- Фактор излучения - исключается.
- Плотность токов значительно меньше, т.к. они распределены по всем стенкам.
- Можно передать большие мощности.
Академик Капица подсчитал, что в трубе (круглой) диаметром 1 м. можно передать всю мощность Красноярской ГЭС.
9.1.1. Типы волноводов
Различают 2 типа:
- односвязные волноводы,
- двухсвязные волноводы.
Порядок связности определяется тем, что поле распределено в какой-то области и не с чем не связано.
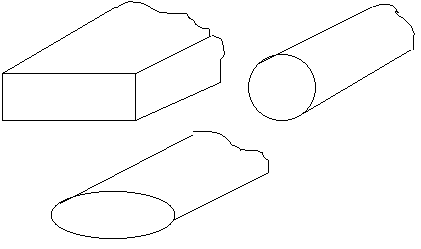
Используются и сложные формы сечения.
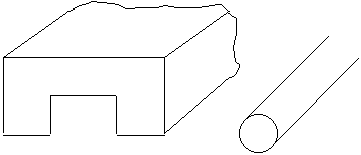
Все это односвязные волноводы. 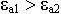
Волны могут распространятся вдоль диэлектрических стержней. Их называют диэлектрическими волноводами, а в оптике - световодами. Металла вообще нет.
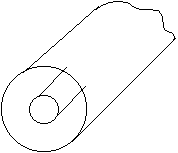
К 2-х связным системам относится коаксиальный волновод. Поле определяется уже двумя проводниками.
9.2. Особенности направляемых ЭМВ
Рассмотрим идеально проводящую плоскость, на которую под некоторым углом падает плоская ЭМВ.
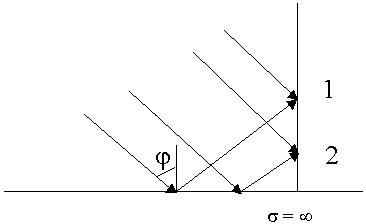
Выясним, как распределено ЭМП над плоскостью, если на нее падает ЭМВ. В т.1 поступает отраженная волна и додающая. В каждой точке над металлической плоскостью ЭМП определяется суперпозицией полей падающих и отраженных. Результат суперпозиции зависит от того, в каких фазах эти поля складываются. Там где фазы одинаковы, будет max, где в противофазе будет min. Из граничных условий. Касательная составляющая вектора Е должна обращаться в 0, поэтому вторую плоскость располагаем в нулях. Физическая основа передачи энергии по волноводам связана с многократным отражением ЭМВ от идеально проводящих стенок. В волноводах могут распространяться ЭМВ с различной структурой поля. Угол j зависит от частоты. С уменьшением частоты угол j уменьшается.
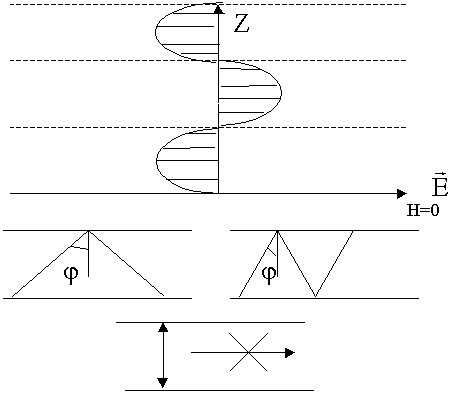
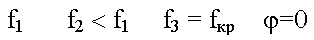
Выводы:
Из качественного рассмотрения. В волноводе существует минимальная частота (критическая fкр). Ниже этой критической частоты энергию по волноводу передавать нельзя f = fкр (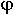 = 0) .
= 0) .
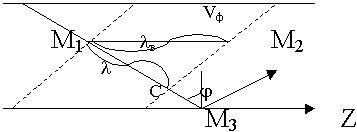
Пример: Если по трубе подать световые волны в критическом режиме, то в конце трубы будет темно. При f 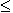 fкр энергия не передается.
fкр энергия не передается.
Покажем, что Vф всегда > С.
Перемещение фронта одинаковых фаз не совпадает с осью волновода. Почему так происходит ? Волна идет под углом многократно отражаясь.
Направление распространения волны из т. М1 в т. М2 показано. Волна распространяется со скоростью света. В т. М1 был 0, через длину волны в т. М2 тоже 0 (расстояние равное  ). За это же самое время вдоль оси расстояние будет пройдено другое (фазовый фронт тот же). Чтобы в т. М3 прийти с той же фазой волне надо двигаться с большей скоростью.
). За это же самое время вдоль оси расстояние будет пройдено другое (фазовый фронт тот же). Чтобы в т. М3 прийти с той же фазой волне надо двигаться с большей скоростью.
Вывод:  в всегда >
в всегда >  , Vф всегда > С.
, Vф всегда > С.
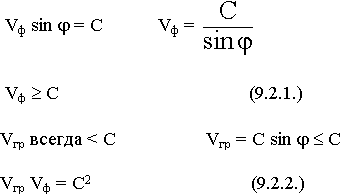
При распространении ЭМВ всегда появляется продольная составляющая либо Е либо Н.
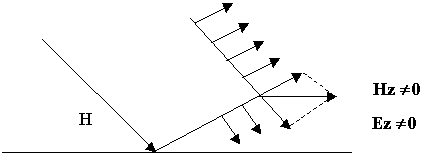
9.3. Волновые уравнения полей в волноводе произвольного сечения
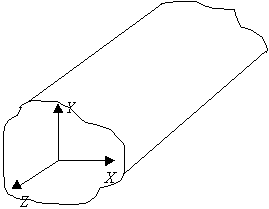
Стенки трубы идеально проводящие. Среда с параметрами 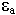 ,
, 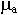 неизменна. Генератор, источник сторонних полей далеко вынесен. Тогда в любой точке этого волновода справедливы уравнения Максвелла:
неизменна. Генератор, источник сторонних полей далеко вынесен. Тогда в любой точке этого волновода справедливы уравнения Максвелла:
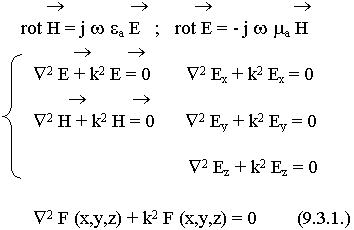
Под F понимаем любую проекцию (Ех Ея и т.д.).
Как можно решить такое уравнение ? Много методов. Один из наиболее удобных - метод разделения переменных по Фурье. Идея метода Фурье заключается в том, что решение ищется в виде произведения функций, каждая из которых зависит от одной из координат. Энергия в волноводе распространяется вдоль оси Z, это обстоятельство мы учтем, выделив функциональную зависимость от Z.
F (x,y,z) = f (x,y) Ф (z) (9.3.2.)
Поскольку решение записано в такой форме, оно должно удовлетворять уравнению.
Проверка:
Ф (z)(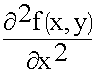 )+ Ф (z)(
)+ Ф (z)( 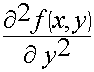 ) + f (x,y) (
) + f (x,y) (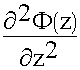 )+ k2 f (x,y) Ф (z) = 0
)+ k2 f (x,y) Ф (z) = 0
(9.3.3.)
Разделим все члены уравнения на коэффициент при k2
(f (x,y) Ф (z))
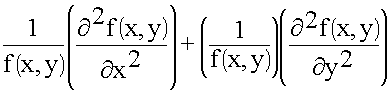 +
+ 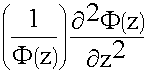 = - k2
= - k2
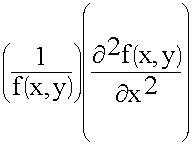 +
+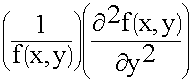 =-k2s (9.3.4.)
=-k2s (9.3.4.)
Индекс “S” означает, что поля изменяются только в поперечных координатах. Это поперечное волновое число.
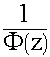 .
.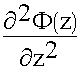 =
= 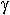 2 - продольное волновое число
2 - продольное волновое число
k2 = k2s + 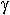 2 (9.3.5.)
2 (9.3.5.)
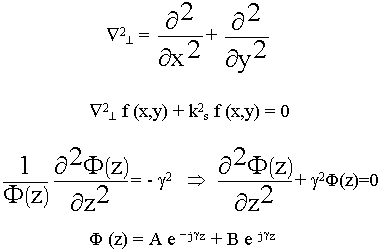
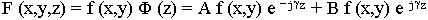
для общего случая
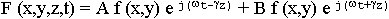
(9.3.6.)
Общее решение представляет собой два волновых процесса с амплитудами А и В и одинаковым распределением поля в поперечном сечении (f (x,y)) и распространяющихся в противоположных направлениях. Поскольку волновод бесконечно длинный, отраженной волны нет, В = 0. Нет физических условий для возникновения отраженной волны. Общая запись полей для произвольного сечения волновода:
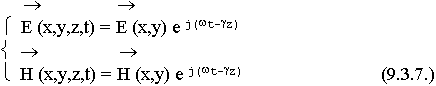
Для конкретизации задаются 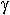 , Е (х,у) Н (х,у)
, Е (х,у) Н (х,у)
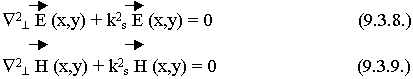
В общем виде уравнения не решаются.
Установим связь между  в свободном пространстве,
в свободном пространстве,  в и
в и  кр.
кр.
В свободном пространстве волновое число:
k = ![]() (9.3.10.)
(9.3.10.)
Продольное волновое число 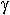 =
= ![]() (9.3.11.)
(9.3.11.)
Поперечное волновое число ks = 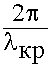 (9.3.12.)
(9.3.12.)
k2 = ks2 + 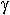 2 (
2 (![]() )2 = (
)2 = (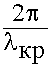 )2 + (
)2 + (![]() )2 (9.3.13.)
)2 (9.3.13.)
 в =
в = 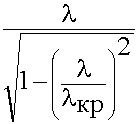 (9.3.14.)
(9.3.14.)
если умножить на f правую и левую часть уравнения (9.3.14) получим:
Vф =  в f =
в f = 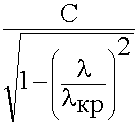 (9.3.15.)
(9.3.15.)
9.4. Классификация ЭМВ
В основе классификации лежит критерий - наличие или отсутствие одной из продольных составляющих. Классификация волн позволяет упростить анализ волн в волноводе и записать все составляющие полей через одну составляющую. Установим связь между поперечными составляющими полей и продольными. Для этой цели спроектируем уравнения Максвелла на оси координат:
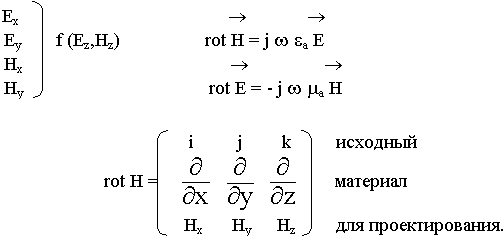
Проекции на оси х, у, z:
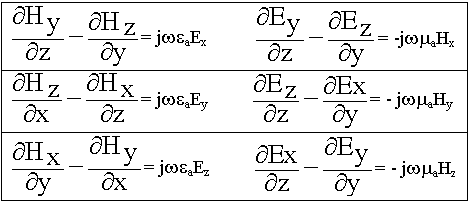
(9.4.1.)
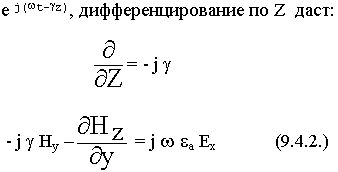

Начнем с уравнения (9.4.2.). Из поперечных составляющих имеем Ех и Ну. Эти же составляющие имеем в (9.4.6.). Из (9.4.2.) находим Ну и подставляем в уравнение (9.4.6.). В результате подстановки составляющие Ех, Еу, Нх, Ну будут выражены следующим образом:
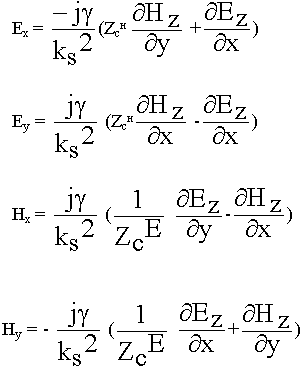
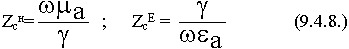
Эти соотношения показывают, что отличные от 0 поперечные составляющие полей в волноводе имеют место, когда одна из продольных составляющих обращается в 0. Различают 4 класса полей.
Первый класс - Электрические волны.
Для этого класса Еz  0 , Hz = 0 (Е - волны)
0 , Hz = 0 (Е - волны)
Второй класс - Магнитные волны.
Для этого класса Hz  0 , Ez = 0 (Н - волны)
0 , Ez = 0 (Н - волны)
Третий класс - Поперечные волны, Т - волны.
Hz = 0 , Ez = 0 (пример плоская ЭМВ)
Четвертый класс - Гибридные волны.
Ez  0 , Hz
0 , Hz  0 (такие волны характерны для световода).
0 (такие волны характерны для световода).
Конкретизируем связь поперечных и продольных составляющих для каждого класса.
9.4.1. Е - волны
Еz  0 , Hz = 0
0 , Hz = 0
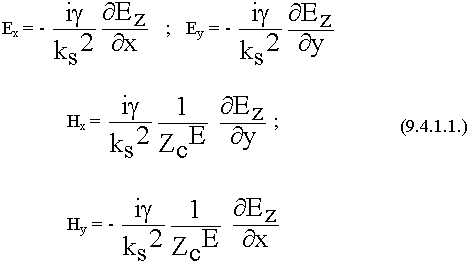
Смысл классификации:
Для расчета полей достаточно найти продольную составляющую.
9.4.2. Н - волны
Ez = 0 , Hz  0
0
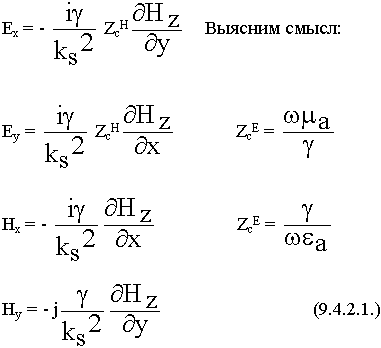
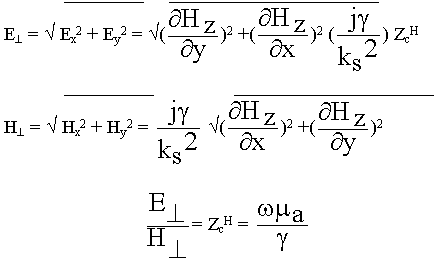
![]() = ZcH- называют характеристическим сопротивлением Н - волны.
= ZcH- называют характеристическим сопротивлением Н - волны.
Аналогично для волны типа Е:
![]() = ZcE =
= ZcE = 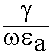 - характеристическое сопротивление волны типа Е. (9.4.2.2.)
- характеристическое сопротивление волны типа Е. (9.4.2.2.)
Что произойдет, если Еz = 0, Hz = 0 ? “Т - волна”. Отличные от 0 поперечные составляющие могут существовать только в одном случае, когда ks = 0, тогда неопределенность (0/0) может дать при раскрытии конечное число.
ks = 0  кр =
кр = ![]() =
= 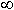
Волна “Т” существует в таких линиях передачи, в которых может поддерживаться устойчивое распределение электрических и магнитных полей в поперечном сечении волновода.
Пример: “Т” волна в коаксиальной линии
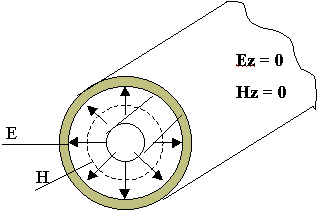
Коаксиальная линия обладает таким свойством. Существует “Т” волна. По такой линии можно передать и постоянный и переменный ток.
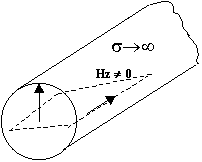
Если будет заряд, он создает поле, которое растекается по поверхности.
Убираем внутренний проводник. Пустая труба. Переменное электрическое поле будет порождать переменное магнитное поле. В поперечном сечении устойчивое распределение полей создать нельзя. В полых трубах волны “Т” распространяться не могут, а только Е, либо Н. В двух связных системах “Т” волны.
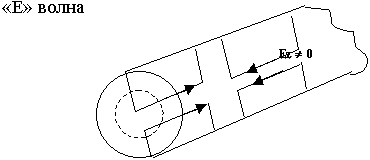
9.5. Прямоугольный волновод
Это металлическая труба прямоугольного сечения.
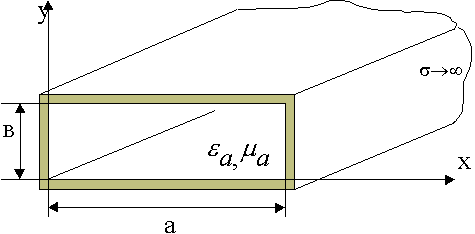
Задача:
2) найти
 кр
крЗнаем, что все поля в волноводе можно рассчитать через продольную составляющую.
“Н” - волны в прямоугольном волноводе.
Требуется найти Hz:
1) Hz = ? 2) Ex , Ey , Hx , Hy - находим через Hz все остальные. 3) конкретизация полей по выполнению граничных условий.
Составляющая Нz удовлетворяет волновому уравнению.
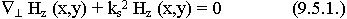
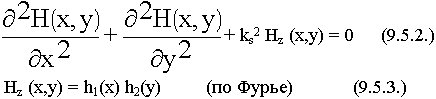
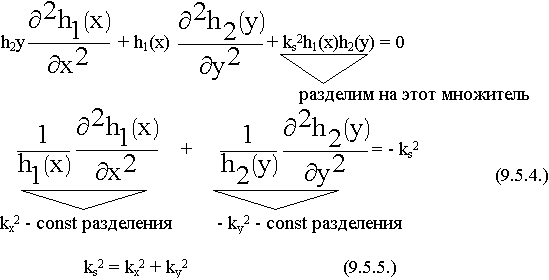
const разделения будем называть поперечными волновыми числами.
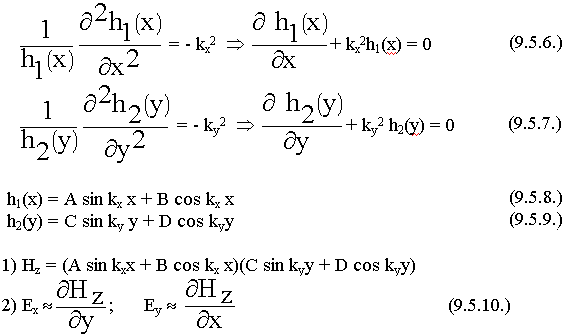
3) Запишем граничные условия для данной задачи.
а) Ex = 0 при у = 0 ; y = b
б) Еу = 0 при х = 0 ; x = a
Ex 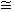 (A sin kxx + B cos kxx) ky (C cos kyy - D sin kyy) (9.5.11.)
(A sin kxx + B cos kxx) ky (C cos kyy - D sin kyy) (9.5.11.)
Накладываем граничные условия:
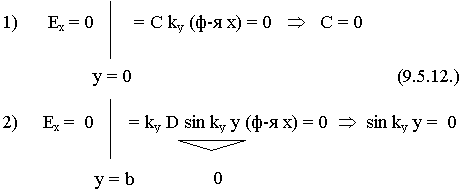
const D нельзя приравнивать к 0, т.к. исчезнет поле Hz, значит sin kyy = 0
kyb = n  ; ky =
; ky = ![]()
n = 0, 1, 2 . . . (9.5.13.)
3) Ey 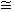
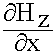
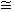 таким же образом можно показать, что const А = 0 из условия
таким же образом можно показать, что const А = 0 из условия
Еу = 0 при х = 0 (9.5.14.)
4) Еу = 0 при х = а
kx = ![]() (9.5.15.)
(9.5.15.)
m = 0, 1, 2 . . .
Hz(x,y) = H0 cos (![]() ) x cos (
) x cos (![]() ) y.еj(w t-g z) ; H0 = B D (9.5.16.)
) y.еj(w t-g z) ; H0 = B D (9.5.16.)
В рамках задачи нельзя определить Н0, т.к. не задана мощность волны на входе. Окончательно другие составляющие полей.
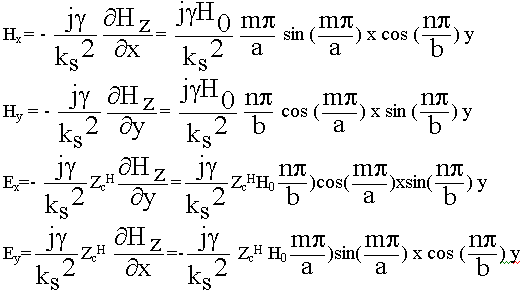
Составляющие Нх, Ну, Ех, Еу умножаем на еj(w t-g z) (9.5.17.)
Соотношения (9.5.5.), (9.5.13.), (9.5.15.) позволяют определить  кр.
кр.
 кр =
кр =![]() ; ks2 = kx2 + ky2 = (
; ks2 = kx2 + ky2 = (![]() )2 + (
)2 + (![]() )2
)2
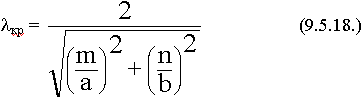
Каждому набору значений индексов m и n соответствует свое распределение поля в волноводе, своя критическая длина волны Нmn. Минимальные значения индексов если m = 0, n = 0, но поля нет. Одновременно индексы не могут быть равны нулю, по частям возможно.
m = 0, 1, 2, 3 . . .
n = 0, 1, 2, 3 . . .
Индексы m и n определяет распределение поля по координатам х, у. С учетом периодичности функции cos, число m имеет смысл - количество полуволн, укладывающихся вдоль а, n - число полуволн, укладывающихся вдоль b. Условием распространения волны в волноводе, является  ген <
ген <  кр. В волноводе бесчисленное множество волн, но не все эти волны могут распространяться. Распространяются только те, которые удовлетворяют условию:
кр. В волноводе бесчисленное множество волн, но не все эти волны могут распространяться. Распространяются только те, которые удовлетворяют условию:  ген <
ген <  кр
кр
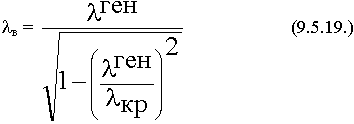
 в – длина волны в волноводе.
в – длина волны в волноводе.
 кр зависит от размеров поперечного сечения а и b, и значения индексов m и n. Максимальная
кр зависит от размеров поперечного сечения а и b, и значения индексов m и n. Максимальная  кр будет для индексов m = 1, n = 0, т.е. волны, у которой значения индексов минимальны.
кр будет для индексов m = 1, n = 0, т.е. волны, у которой значения индексов минимальны.
a > b ; m = 1 , n = 0
Максимальной  кр, обладает волна Н10*
кр, обладает волна Н10*  кр = 2а. У всех других волн критическая длина волны меньше, волну Н10 называют основной волной в волноводе. Она наиболее часто используется.
кр = 2а. У всех других волн критическая длина волны меньше, волну Н10 называют основной волной в волноводе. Она наиболее часто используется.
Выделим ось, где откладываем  .
.
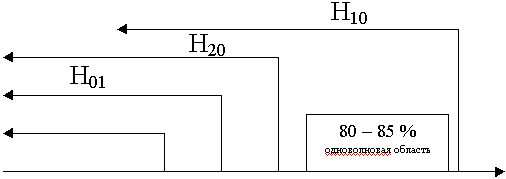

Диаграмма спектра волн в прямоугольном волноводе.
Если  ген > 2a, то волны не распространяются.
ген > 2a, то волны не распространяются.
m = 1, n = 0 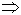 Н10
Н10  кр = 2а
кр = 2а
m = 2 , n = 0 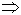 H20 ,
H20 ,  кр = а
кр = а
m = 0 , n = 1 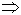 H01 ,
H01 ,  кр = 2b
кр = 2b
Стандартный волновод 2b < a для волны Н10:
a 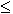
 ген
ген 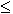 2a - одноволновый режим.
2a - одноволновый режим.
Диапазон использования одноволновой области 80 - 85 %. Не рекомендуется подходить к критическому режиму (справа и слева).
Предположим, имеем прямоугольный волновод, на входе этого волновода имеется генератор СВЧ диапазона и возбудитель волны.
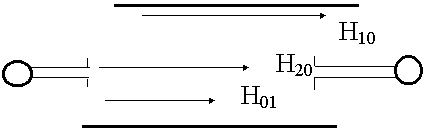
Возбудитель может возбудить любую волну (Н10, Н20 и т.д.). На выходе стоит похожее устройство, принимающее сигнал индикатора. Эксперимент заключается в следующем: генератор перестраивается в широком диапазоне частот.
Если  ген > 2а , индикатор ничего не показывает, энергия не идет по волноводу.
ген > 2а , индикатор ничего не показывает, энергия не идет по волноводу.
 ген
ген 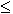 2а
2а 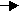 Н10
Н10
 ген < а
ген < а 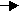 Н20 часть энергии идет на волне Н20
Н20 часть энергии идет на волне Н20
(условно из 10 Вт генер. 8 Вт передается волной Н20)
 ген < 2b
ген < 2b 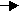 H01
H01
Специалисту нужно, чтобы была одна волна, для этого нужно уменьшать поперечное сечение волновода (частота генератора остается неизменной).
В реальных условиях нереально создать условия, когда волны существуют в волноводе независимо друг от друга. Многоволновое распространение нежелательно, т.к. информация из канала в канал передается. Стараются избежать взаимной связи между волнами и использовать одноволновый режим. Волна - mode - по английски. Говорят одномодовый, многомодовый.
9.5.1. Основная волна в прямоугольном волноводе. Преимущества волны Н10
- Имеет место максимальный диапазон одноволновой передачи.
- При передаче энергии на волне Н10 потери энергии волны минимальны.
- Поперечные размеры волновода наименьшие при передаче волны типа Н10.
Выпишем составляющие волны Н10
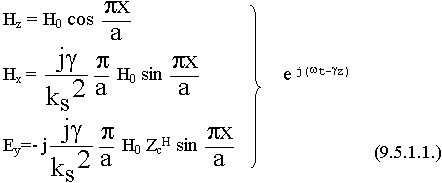
Восстановим из уравнений распределение силовых линий Е и Н поля для основной волны. Рассмотрим поперечное сечение волновода.
Электрическое поле волны Н10 имеет одну составляющую Еу, она max в середине волновода.
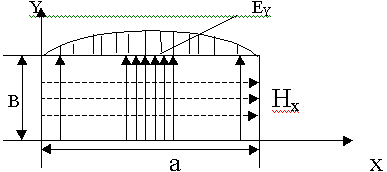
Поле Е направлено от одной стенки к другой. Магнитное поле имеет 2 составляющие Нх и Нz.
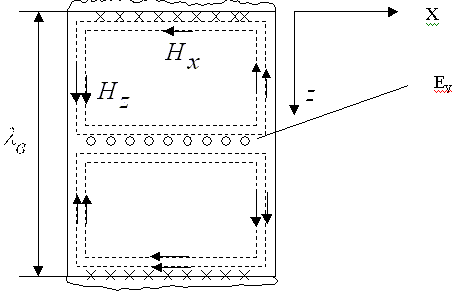
У боковых стенок волновода НZ максимальна. В силу непрерывности линий магнитного поля Нz замыкается через Нх (Нz переходит в Нх). Эта картинка перемещается в волноводе со скоростью:
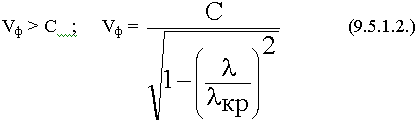
9.5.2. Токи в стенках волновода
В силу закона электромагнитной индукции переменное магнитное поле вблизи проводников возбуждает электрический ток. Переменное магнитное
поле вблизи стенок будет создавать токи проводимости. Посмотрим как протекают токи ? Знание токов позволяет решить 2 задачи:
- Рассчитать потери в волноводе.
- Определить как осуществить разрез стенок, чтобы из волновода извлечь энергию, либо наоборот, не нарушать распределения токов.
Установим связь между плотностью поверхностных токов и напряженностью магнитного поля. Разберем простейший случай.
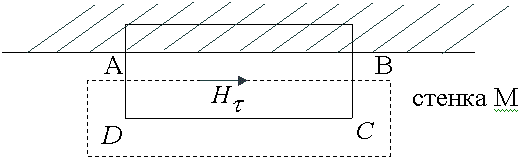
Вблизи стенки волновода магнитное поле всегда имеет только касательную составляющую. Применим закон полного тока к контуру, часть которого находится в металле, часть нет.
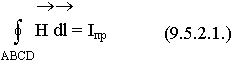
![]() определим по частям:
определим по частям:
ABCD
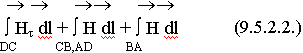
Предположим контур мал, Нt всегда перпендикулярна СВ, АD. Участок АВ находится в глубине металла. В силу поверхностного эффекта токи поверхностные быстро затухают. Значение магнитного поля на участке ВА очень мало. Этот интеграл обращается в 0.
Для малых АВСD 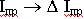
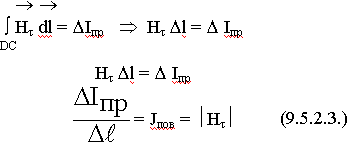
Плотность поверхностного тока числено равна касательной составляющей магнитного поля и они взаимно перпендикулярны.
Чтобы восстановить распределения токов надо воспользоваться разверткой.
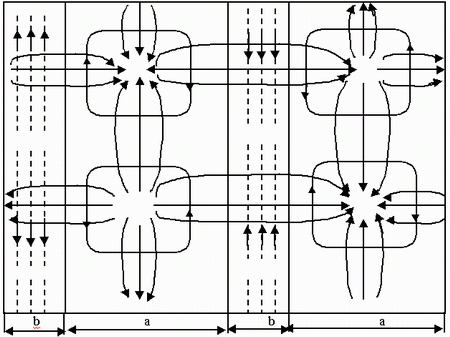
Составляющая Нх порождает ток J z. В широкой стенке 2 тока, продольный Jz, поперечный Jy. В боковой стенке поперечные токи Jy.
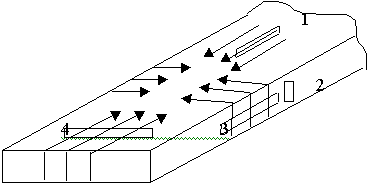
Нх  Jz , Hz
Jz , Hz 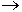 Jx
Jx
Если щель в волноводе пересекает токи, то такая щель будет хорошо излучать, если щель вдоль токов, то она не излучает. Щели 1, 2 - не излучают; 3,4 - излучают.
9.5.3. Передача энергии по волноводу
Рассмотрим процесс передачи энергии на примере основной волны Н10:
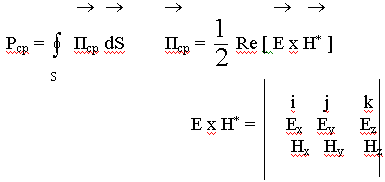
Пz ср = ![]() Ех Ну* - ЕуНх* = - Еу Нх .
Ех Ну* - ЕуНх* = - Еу Нх .![]() Энергия, передаваемая вдоль волновода определяется только поперечными составляющими полей. (9.5.3.1.)
Энергия, передаваемая вдоль волновода определяется только поперечными составляющими полей. (9.5.3.1.)
-EyHx* =(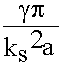 )2 H02 ZcH sin2(
)2 H02 ZcH sin2(![]() ) (9.5.3.)
) (9.5.3.)
Вычислим теперь среднюю мощность:
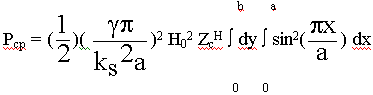
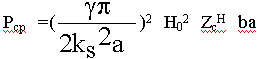 средняя мощность, передаваемая в волноводе. (9.5.3.3.)
средняя мощность, передаваемая в волноводе. (9.5.3.3.)
Передаваемая мощность по волноводу зависит от амплитуды продольной составляющей магнитного поля Рср 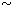 Н02 . Мы можем увеличить передаваемую мощность, увеличивая размеры волновода. Найдем Н0:
Н02 . Мы можем увеличить передаваемую мощность, увеличивая размеры волновода. Найдем Н0:
H0 =  (9.5.3.4.)
(9.5.3.4.)
Эта составляющая числено равна поперечному току в стенках волновода. Она возбуждает в стенках волновода  ей ток.
ей ток.
Н0 = | Jx| = | Jy|
Ey = - (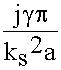 ) ZcH H0 sin
) ZcH H0 sin ![]()
Ey0 = 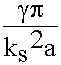 ZcH (
ZcH (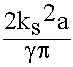 ) .
) . 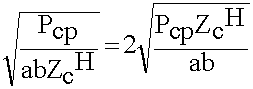 > (9.5.3.5.)
> (9.5.3.5.)
Напряженность электрического поля возрастает с ростом передаваемой по волноводу мощности.
Епробmax 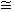 30
30 ![]() для воздуха
для воздуха
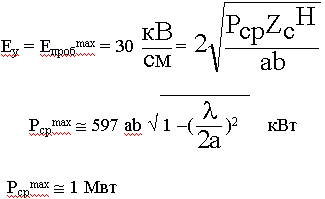
a , b - см.
a x b = 2,3 x 1,0 см Рсрmax 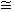 1 Мвт
1 Мвт
При проектировании различных устройств обязательно делают запас прочности:
Рраб = (0,2 ¸ 0,3 ) Рсрmax
Один из путей повышения уровня передаваемой мощности связан с заполнением его средой, имеющей более высокое значение пробивного напряжения, чем у воздуха.
9.5.4. Потери энергии в волноводе
Можно выделить 3 основных фактора, которые несут ответственность за потери энергии:
- Конечная проводимость стенок волновода. За счет этого часть токов в стенках волновода преобразуется в тепло, греет волновод (омические потери).
- Несовершенство среды, которая заполняет волновод (диэлектрические потери).
- Связан с нарушением однородности стенок. Из-за непрерывной эксплуатации или других факторов образуются какие-то щели и через них проходит излучение энергии.
Любая из этих причин приводит к тому, что 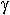 - постоянная распространения величина комплексная, как и в случае плоских волн.
- постоянная распространения величина комплексная, как и в случае плоских волн.
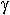 =
= 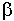 - j
- j ;
;
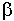 - фазовая постоянная
- фазовая постоянная
 - коэффициент затухания.
- коэффициент затухания.
Предположим, что имеется отрезок волновода.
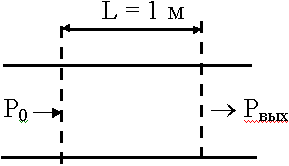
На входе Р0, на выходе Рвых. Сколько теряется энергии ?
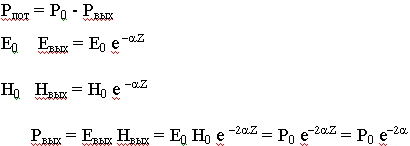
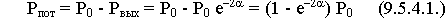
В случае, когда параметр  << 1, тогда:
<< 1, тогда:
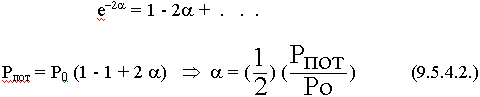
Основным фактором потерь являются омические потери.
Нужно собрать все потери в стенках волновода:
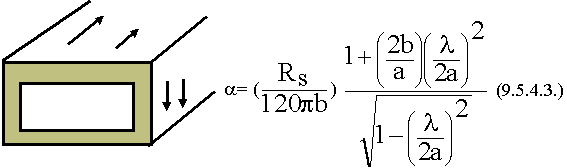
Rs - поверхностное сопротивление.
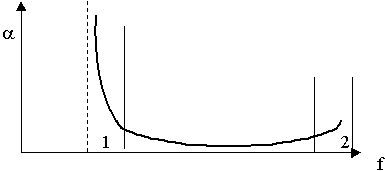
В области (1) потери большие, так как частота близка к критической. А дальше с ростом частоты растет поверхностное сопротивление металла, т.е. работает поверхностный эффект. Расчет по формуле (9.5.4.3.) дает чуть меньше коэффициент затухания, чем на самом деле. Поскольку мы не учитываем качество обработки поверхности. Для уменьшения потерь нужно высокое качество обработки и материал с максимально большой проводимостью. С этой целью используется покрытие стенок серебром. Реально достижимые потери (0,1 ¸ 0,01 ) дБ/м.
Волновод, заполненный диэлектриком 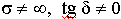
Rs = 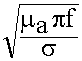
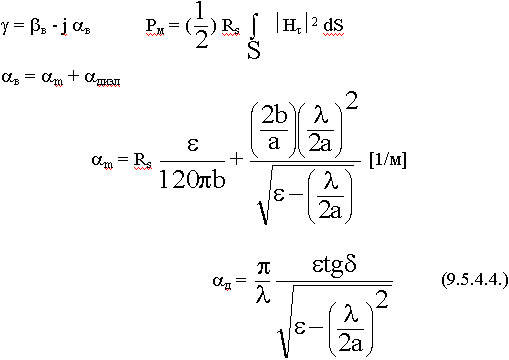
9.5.5. Е - волны в прямоугольном волноводе
Наряду с волнами Н - типа, в прямоугольном волноводе могут распространяться волны Е- типа. Анализ волн проводится по той же схем, что и в случае Н - волн.
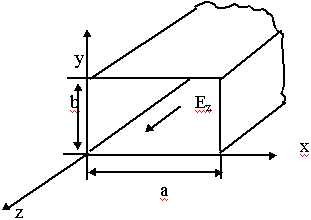
Е - волны Еz  0, Hz = 0
0, Hz = 0
Решается уравнение:

Результатом решения будет:
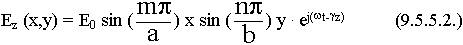
Запись удовлетворяет граничным условиям на стенках волновода.
m = 1, 2, 3 . . . m  0
0
n = 1, 2, 3 . . . n  0
0
Если одно из чисел m или n обращается в 0, то волны не будет.
Еe = 0 при х = 0, х = а, Ех = 0 при у = 0, у = b.
Каждому набору индексов m и n соответствует своя структура поля в поперечном сечении, каждая из волн имеет свою  кр.
кр.
 кр =
кр = 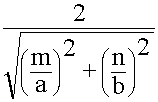 (9.5.5.3.)
(9.5.5.3.)
Выражение (9.5.5.3.) совпадает с выражением (9.5.18) для Н - волн. Волны Н и Е с одинаковыми индексами m и n имеют одно значение  кр и Vф. Пример: Н11, Е11 - одинаковые
кр и Vф. Пример: Н11, Е11 - одинаковые  кр , Vф. Волны, имеющие одинаковые Vф,
кр , Vф. Волны, имеющие одинаковые Vф,  кр, но различные структуры в поперечном сечении называются вырожденными.
кр, но различные структуры в поперечном сечении называются вырожденными.
У волны Е индексы m и n не равны 0. У “Н” один из индексов может быть равен нулю. Из “E” - волн самая простая Е11.
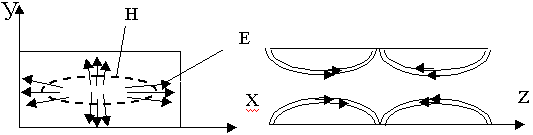
Магнитное поле для волн типа Е всегда в плоскости поперечного сечения волновода, т.к. линии Е всегда перпендикулярны Н.
Для волн “Е” характерно присутствие Еz вдоль оси Z. Волноводы с волной “Е” используются в ускорителях и в электровакуумных приборах (в тех случаях, где необходимо осуществить взаимодействие элементарных частиц с электромагнитным полем).
9.6. Круглые волноводы
Представляют собой металлическую трубу круглого сечения. Для изучения полей в каждой точке надо применить цилиндрическую систему координат.
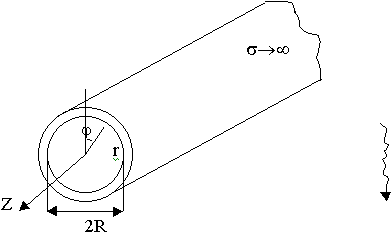
Особенности: своеобразная запись граничных условий. Внутри поверхности, любая касательная составляющая (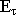 = 0) электрических полей должна обращаться в 0. Требования для граничных условий.
= 0) электрических полей должна обращаться в 0. Требования для граничных условий.
1)  = 0 при r = R.
= 0 при r = R.
2) 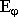 = 0 при r = R.
= 0 при r = R.
9.6.1. Волны “Е” типа в круглом волноводе
Еz  0, Hz = 0
0, Hz = 0
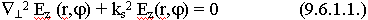
Это уравнение должно решаться в цилиндрических координатах.
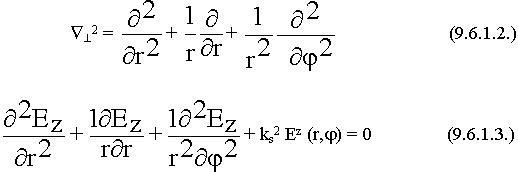
Решаем по м. Фурье с разделением переменных:
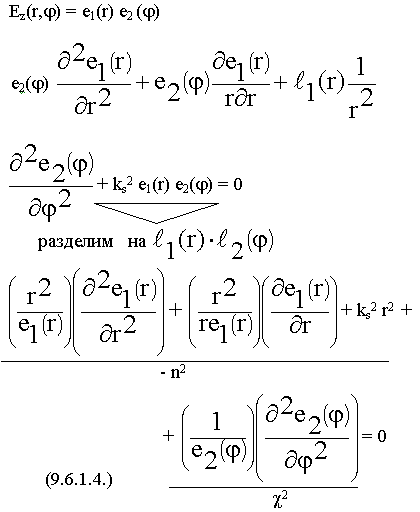
Результат разделения: n2 = 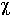 2 – константы разделения
2 – константы разделения
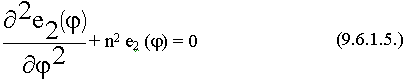
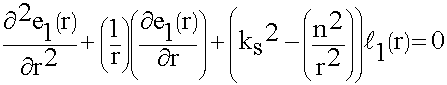 (9.6.1.6.)
(9.6.1.6.)
Поделим на r2.Решением первого уравнения ( 9.6.1.5.) являются тригонометрические функции. Из (9.6.1.5.):
е2( ) = A sin n
) = A sin n  + B cos n
+ B cos n  (9.6.1.7.)
(9.6.1.7.)
Решением уравнения (9.6.1.6.) являются функции Бесселя и Неймана:
Jn - функция Бесселя.
Nn - функция Неймана.
У функций Бесселя есть значения аргументов, при которых функции обращаются в 0. Эти значения называют корнями.
 nm
nm
n - порядок функции Бесселя.
m - порядковый номер корня.
Поскольку в любой точке поля должны быть конечны, то коэффициент D = 0, т.к. функция Неймана может давать бесконечно большое значение функции:
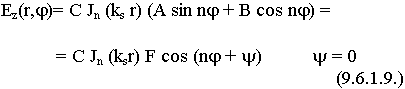
Начало отсчета угла можно начать с любого места:
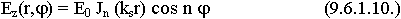
Выясним, какие значения принимает “n” - распределение поля по азимуту. Сделав оборот по углу j на 3600 мы попадаем в ту же точку, значения полей не должны изменяться. Из условий периодичности параметр n всегда целое число (n = 0, 1, 2). Для нахождения  кр используем граничные условия по составляющим Еz. Еz (r,
кр используем граничные условия по составляющим Еz. Еz (r,  ) при r = R должно быть равно нулю.
) при r = R должно быть равно нулю.
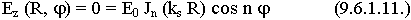
Это возможно в одном случае, когда значение аргумента равно корню функции:
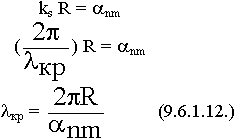
Значения корней функции Бесселя затабулированы. Минимальным значением корня обладает функция Бесселя нулевого порядка  01.
01.
 01 = 2,405 ;
01 = 2,405 ;  кр =
кр = 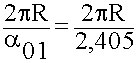 =2,61 R =
=2,61 R =  кр (9.6.1.13.)
кр (9.6.1.13.)
Каждому значению n и m соответствует свое распределение поля. Первый индекс указывает сколько полуволн укладывается по азимуту, а второй по радиусу (диаметру).
Простейшая волна Е01.
Е11  Е01 преобразуется волна Е11 в прямоугольном волноводе в волну Е01 круглого волновода. При деформации стенок волновода, линии вектора Е всегда перпендикулярны проводнику.
Е01 преобразуется волна Е11 в прямоугольном волноводе в волну Е01 круглого волновода. При деформации стенок волновода, линии вектора Е всегда перпендикулярны проводнику.
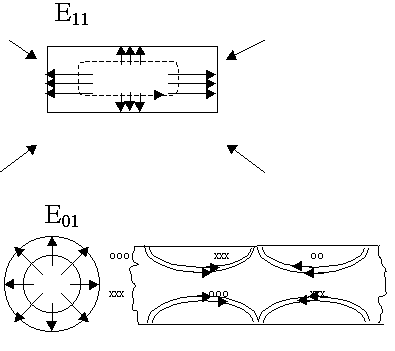
Волна Е01 называется симметричной. Используется во вращающихся сочленениях радиолокационных станций.
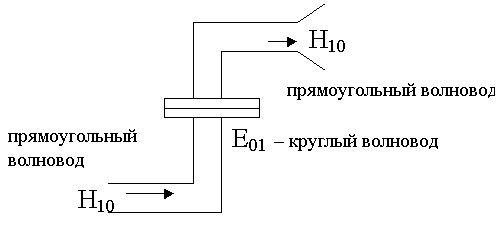
Вращающееся сочленение в радиолокационных станциях.
9.6.2. Волны “Н” типа в круглом волноводе
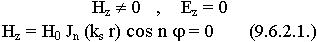
Граничные условия в случае волны типа Н:
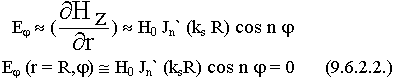
Это требование выполняется, когда значение аргумента ksR равно корню производной функции Бесселя.
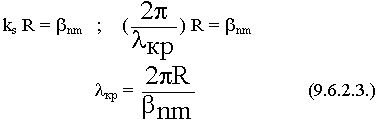
Каждому значению n и m соответствует своя структура, своя  кр.
кр.
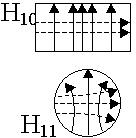
 крmax при n = 1 , m =
крmax при n = 1 , m = 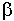 11 = 1, 84
11 = 1, 84  кр = 3,41 R
кр = 3,41 R
Волна Н11 - является основной волной круглого волновода. Волну Н11 можно получить путем деформации волны Н10 в прямоугольном волноводе.
9.6.3. Волна Н01 в круглом волноводе. Возможности применения ее в дальней связи
Н01 - симметричная магнитная волна соответствует значению корня функции Бесселя 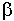 01 = 3,83 ;
01 = 3,83 ;
 кр =
кр = 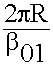 = 1,64 R
= 1,64 R
Критическая длина волны ( кр) у Н01 меньше чем у Н11 и Е01. По отношению к волнам Н11 и Е01 волна Н01 является высшей.
кр) у Н01 меньше чем у Н11 и Е01. По отношению к волнам Н11 и Е01 волна Н01 является высшей.
Структура поля Н01
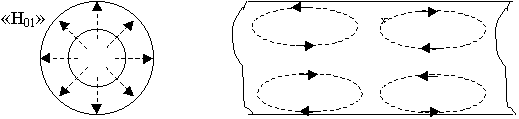
У волны Н01 имеет место аномальные поведение затухание в зависимости от частоты.
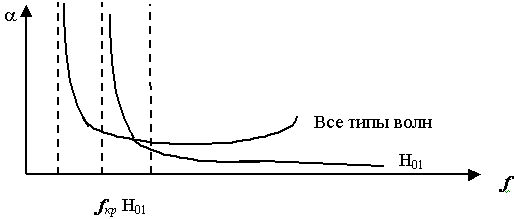
Для специалистов связи, это большое преимущество. С увеличением частоты расширяется возможность увеличения числа каналов. Увеличивается дальность связи за счет уменьшения потерь.
Почему происходит уменьшение затухания от частоты? Затухание связано с токами в стенках волновода.
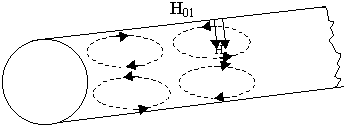
У стенок волновода находится продольная составляющая Нz. Как токи направлены ? Линии тока всегда перпендикулярны Нz, значит есть только кольцевые токи в стенках волновода. Источником этих токов являются продольные составляющие магнитного поля Нz.
Для всех волн характерно, что с увеличением частоты продольные составляющие полей Нz и Ez убывают.

Физическое объяснение. У волн других типов существуют и продольные и поперечные токи, которые возбуждаются продольными и поперечными магнитными полями. Наличие продольных токов приведет к увеличению потерь.
Пример:
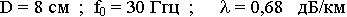
При усилении на 90 дБ длина усилительного участка Lус = 130 км.
f0 = 50 Ггц для тех же данных  = 0, 28 дБ/км.
= 0, 28 дБ/км.
Lус = 320 км
Основная трудность реализации идеи дальней связи заключается в том, что Н01 является высшим типом. При D = 6 см и  0 = 6 мм существует одновременно 300 типов волн.
0 = 6 мм существует одновременно 300 типов волн.
Это неприятный момент. В реальных условиях происходит взаимодействие волн. Часть энергии волны Н01 передается волнами других типов. Высшие типы волн быстро затухают, значит и часть энергии волны Н01 - тоже затухает.
Вопрос: Как бороться с таким явлением ?
- В волноводе можно сделать пленку, которая оказывает сильное влияние на высшие типы и не оказывает на Н01.
- В волноводе кольцевые токи. Можно сделать волновод из колец.
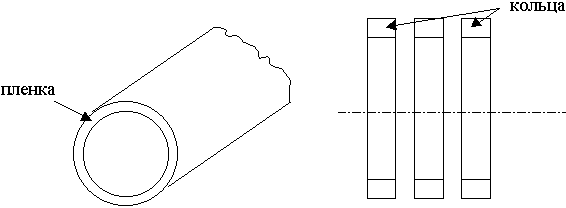
Для кольцевых токов Н01 это не страшно, для других типов волн будет разрыв продольных токов. Наборный волновод сделать сложно, поэтому делают спиральный волновод. Созданы опытные волноводы.
Спектр волн в круглом волноводе.
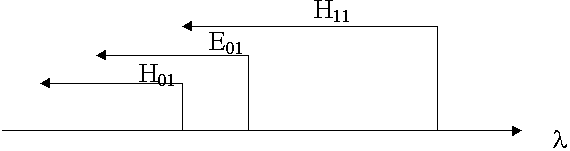
9.7. Волноводы сложного сечения
Наибольшее применения нашли эллиптические волноводы. Идея пришла из биологии (рыба плывет извиваясь, но поперечное сечение не изменяется).
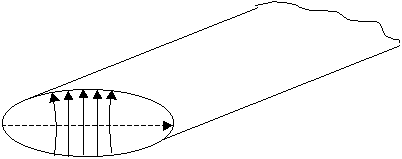
Достоинства эллиптических волноводов:
- Волновод можно наматывать на барабаны.
- Существует устойчивая поляризация передаваемой волны.
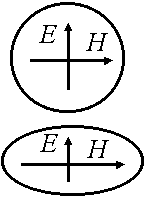
В режиме передачи и режиме приема строго должны быть выполнены условия неизменного поперечного сечения волновода.
В эллиптическом волноводе поляризация вертикальная и горизонтальная развязаны между собой.
“П” - образные волноводы.
Достоинство волноводов:
- Обычно прямоугольный волновод имеет небольшую полосу рабочих частот.
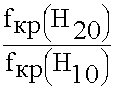 = 2
= 2
Системы многоканальной связи работают в более широком диапазоне.
Введение выступа в широкой стенке не оказывает влияние на волну Н20, на волну Н10 оказывает сильное влияние. За счет концентрации поля можно увеличивать широкополосность.
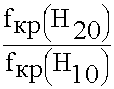 = 5 ¸ 6
= 5 ¸ 6
Недостатки “П” - образных волноводов:
- Сильная концентрация поля, плотность токов растет, потери возрастают.
- Может возникнуть пробой в месте большой концентрации поля. Падает передаваемая мощность.
9.8. Возбуждение волноводов
Возбуждение волноводов осуществляется с помощью элементарных электрических и магнитных излучателей.
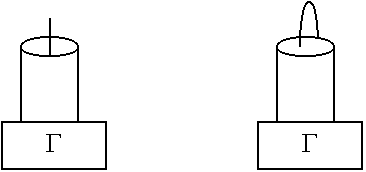
Для возбуждения волны в волноводе используется 3 принципа:
- Линии Е, создаваемые возбудителем, должны совпадать в некотором сечении волновода с линиями Е возбуждаемого типа волны.
- Линии Н, создаваемые возбудителем, совпадают с линиями типа Н возбуждаемого типа волны.
- Токи, создаваемые возбудителем, должны совпадать с токами в стенках волновода требуемого типа.
Если одно из условий удовлетворяется, то можно возбудить волну в волноводе, но это еще не гарантирует, что именно одна волна будет. В качестве возбудителя возьмем элементарный электрический излучатель.
Штырь параллелен вектору Е
1)
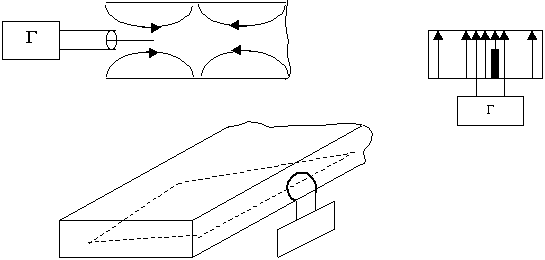
2)
Для того, чтобы от возбудителя волны распространялись в одну сторону, нужно поставить стенку на расстоянии ![]() . В этом случае будет синфазное сложение волн падающих и отраженных.
. В этом случае будет синфазное сложение волн падающих и отраженных.
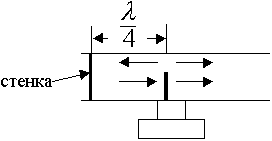
10. Линии передачи оптического диапазона
10.1. Преимущества световодов
- Световоды обладают большой пропускной способностью (многоканальностью).
- Световоды не подвержены воздействию внешних ЭМП (наводки, молнии и т.д.).
- Малогабаритны (вес и масса малы).
- Отсутствие металлических проводников, нет металла дорогостоящего (медь, серебро, золото).
10.2. Основные типы световодов
1. Планарный световод - представляет собой тонкую стеклянную пленку (плоскую).
В увеличенном виде выглядит следующем образом:
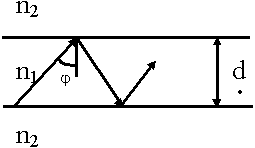
n1 - всегда > n2 - показатель преломления окружающей cреды, n1 - показатель преломления пленки. n1 > n2
Такой слой может направлять ЭМВ вдоль границы. Физической основой передачи энергии оптического диапазона во всех типах световодов является эффект полного внутреннего отражения. Если  >
>  кр, то волна распространяется, если это условие не выполняется, то часть энергии выходит в окружающее пространство и передача энергии не возможна.
кр, то волна распространяется, если это условие не выполняется, то часть энергии выходит в окружающее пространство и передача энергии не возможна.
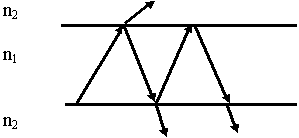
Основное назначение планарных световодов - реализация на их базе различных устройств по обработке информации в оптическом диапазоне (фильтры, различные делители энергии, направленные ответвители и т.д.).
2. Волоконный световод - тонкая стеклянная двухслойная нить в поперечном сечении. Имеет вид:
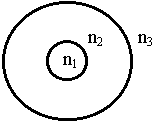
n1 - показатель преломления сердцевины;
n2 - показатель преломления оболочки;
n3 - показатель преломления окружающей cреды.
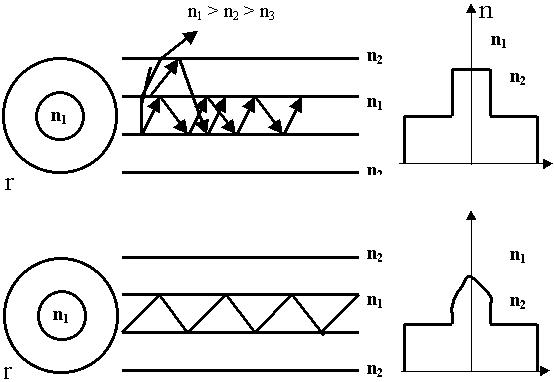
Различают ступенчатые и градиентные световоды. Если дискретно меняется показатель преломления, то такое волокно называется ступенчатым световодом.
Другая разновидность световода - световод с непрерывным распределением показателя преломления, их еще называют градиентными. Они отличаются от ступенчатых световодов тем, что показатель изменяется по определенному закону.
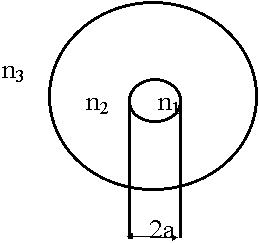
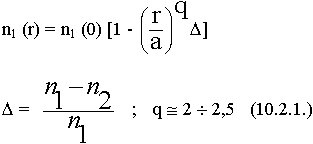
показатель степени
В центре n1 max и убывает по параболе к оболочке. Такой световод может фокусировать.
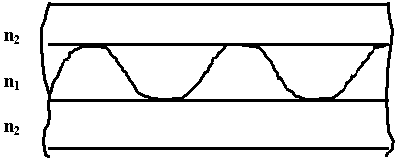
В настоящее время строгие методы расчета базируются на 2-х подходах:
- Используют геометро-оптическое представление процессов в световодах.
В основе лежит первый и второй закон Снеллиусса.
- Используют полевое описание (представление) при распространении волн.
При работе с планарными световодами чаще используют первый подход (методы геометрической оптики). Для анализа волоконных световодов используют второй метод.
10.3. Особенности поперечных структур поля в световодах
Фазовая скорость в световодах. Vф 
![]() =
= 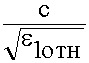 < c
< c
Vф всегда меньше скорости света (с)
m = ![]() - коэффициент замедления.
- коэффициент замедления.
m всегда > 1. Световод замедляет волны.
Vф = 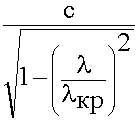 - в волноводе
- в волноводе
m = ![]() =
= 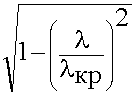 < 1 (10.3.1.)
< 1 (10.3.1.)
Волновод ускоряет волны.
Составляющие полей удовлетворяют условию:
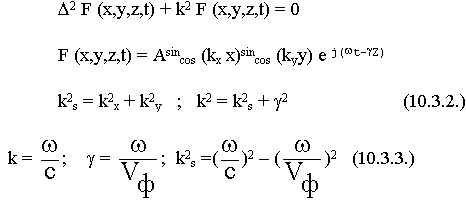
Рассмотрим выражение (10.3.3.) для световодов, когда Vф < c, то :
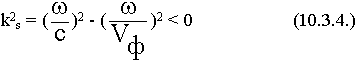
Величина ks - мнимая.
Формально отсюда, что kx и ky чисто мнимые величины.
kx = j  ; ky = j
; ky = j 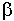 - могут оба сразу.
- могут оба сразу.
или либо kx, либо ky
sin j  x = j sh
x = j sh  x ; cos j
x ; cos j  x = ch
x = ch  x
x
В поперечном сечении поля описываются непериодическими функциями (гиперболическими).
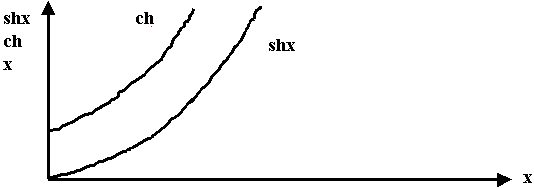
Вопрос: Что означает, что так распределено поле - Е ?
Что надо сделать чтобы было max поле?
Ответ: Сделать стенку из диэлектрика.
В линиях передачи с медленными волнами поле распределено неравномерно, оно прижато к границе раздела.
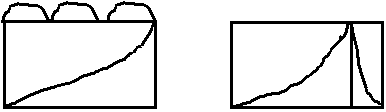
Такая ситуация напоминает поверхностные волны, которые как бы прилипают к поверхности.
10.4. Планарный световод
Задача ставится следующим образом:
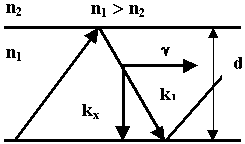
Имеется пластинка, толщиной d. На границе раздела сред выполняется условие полного внутреннего отражения. Цель определить критический размер d и  кр, когда слой может направлять электромагнитные колебания оптического диапазона.
кр, когда слой может направлять электромагнитные колебания оптического диапазона.
Выделим основные параметры внутри слоя. Направление волнового процесса вдоль оси Z - 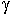 , поперечное волновое число - kx. В поперечном сечении в результате отражения от границ раздела устанавливается стоячая волна.
, поперечное волновое число - kx. В поперечном сечении в результате отражения от границ раздела устанавливается стоячая волна.
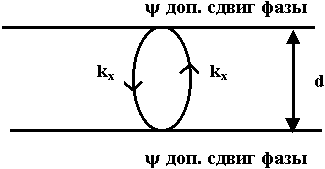
При отражении от границы раздела появляется дополнительный сдвиг фаз 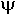 . Сколько же всего ? Вычислим общий набег фазы:
. Сколько же всего ? Вычислим общий набег фазы:
1) kx d + 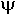 (от верхней до нижней)
(от верхней до нижней)
2) kx d + 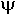 (от нижней до верхней)
(от нижней до верхней)
Синфазное сложение будет тогда, когда целое число
kx d + 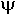 + kx d +
+ kx d + 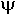 = 2
= 2 (m - 1)
(m - 1)
m = 1 , 2 . . . (10.4.1.)
или kx d = (m - 1)  (10.4.2.)
(10.4.2.)
Выражение (10.4.2.) можно использовать для расчета критической длины волны, передаваемой в пластинке. Представим величину kx через параметры среды и пластинки:
kx = k1 cos  ;
; 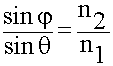 (10.4.3.)
(10.4.3.)
Поскольку явление полного внутреннего отражения, то 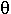 = 900 sin
= 900 sin 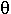 = 1
= 1
sin  =
= ![]()
 0 =
0 =  0кр
0кр
cos  =
= 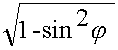 =
=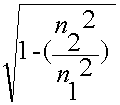 (10.4.4.)
(10.4.4.)
Окончательно:
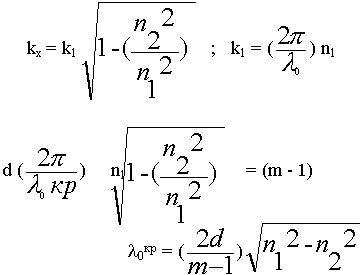
 0кр зависит от размеров (толщины) и разности показателей преломления,
0кр зависит от размеров (толщины) и разности показателей преломления,  0кр при
0кр при
m = 1 становится, б/б. Волновой процесс идет на любой частоте.
Каждому значению m соответствует своя критическая длина волны и своя структура поля, своя мода.
При m = 1 ,  кр =
кр =  . Такая волна называется основной волной планарного световода. Это несколько искаженная самой пластинкой плоская ЭМВ. У плоской ЭМВ нет критического режима, она существует на любых частотах.
. Такая волна называется основной волной планарного световода. Это несколько искаженная самой пластинкой плоская ЭМВ. У плоской ЭМВ нет критического режима, она существует на любых частотах.
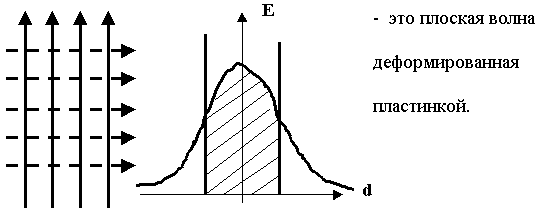
плоская ЭМВ m = 1
Если m = 2
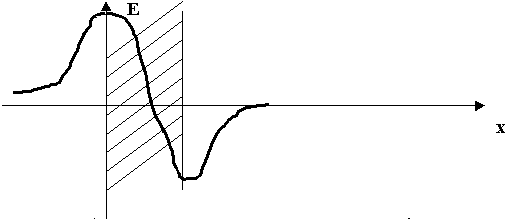
Все остальные типы будут иметь конечные значения  кр и начинают распространяться выше своих критических частот. Будущие системы будут работать в одномодовом режиме, чтобы высшие типы не распространялись. Пластинку надо делать с высоким качеством и очень тонкую (1 - 2 мкМ). Специалисты делают по другому. Они обеспечивают уменьшение
кр и начинают распространяться выше своих критических частот. Будущие системы будут работать в одномодовом режиме, чтобы высшие типы не распространялись. Пластинку надо делать с высоким качеством и очень тонкую (1 - 2 мкМ). Специалисты делают по другому. Они обеспечивают уменьшение  0кр при заданной толщине d , уменьшением разности показателей преломления
0кр при заданной толщине d , уменьшением разности показателей преломления
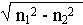
на f1 >> fкр. Идет процесс передачи по световоду (угол велик). условие полного внутреннего отражения выполняется.
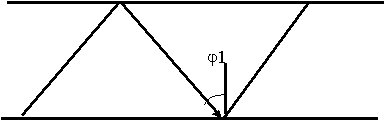
f2 < f1  2 <
2 <  1
1
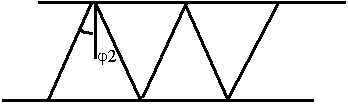
f3 < fкр - условие для выполнения полного внутреннего отражения нет, часть волны уходит в окружающую среду.

10.5. Оптическое волокно
Проследить и выделить результат многократного отражения в цилиндре сложно. Рассмотрим волокно, представляющее собой бесконечную длинную нить.
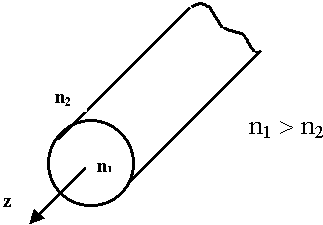
Рассмотрим задачу для Е - волн.
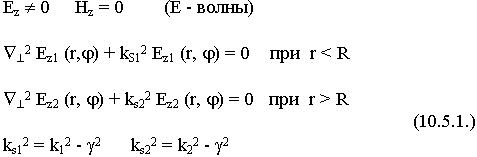
10.5.1. Симметричные волны в оптическом волокне
Рассмотрим частный случай. Симметричные волны в оптическом волокне, симметричные Е - волны, ![]() = 0. Это соответствует случаю, когда азимутальный индекс, который определяет порядок функции Бесселя n = 0. В цилиндрических координатах в первой среде при r < R.
= 0. Это соответствует случаю, когда азимутальный индекс, который определяет порядок функции Бесселя n = 0. В цилиндрических координатах в первой среде при r < R.
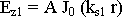 - решение волновых уравнений внутри волокна (10.5.2.)
- решение волновых уравнений внутри волокна (10.5.2.)
Для поля вне волокна должно выполняться условие уменьшения поля с удалением от стержня. В классе функций Бесселя надо искать условие убывания. Единственной функцией среди цилиндрических (Неймана, Ханкеля и др.) является функция Макдональда Кn (x), у которой при больших значениях аргументов функция уменьшается:
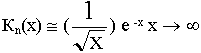 - функция непериодическая. (10.5.3.)
- функция непериодическая. (10.5.3.)
Решение для составляющих Еz2:
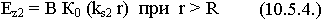
Если известны продольные составляющие, то можно выразить поперечные:
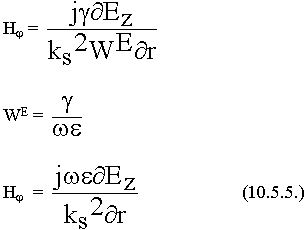
Вычислим две составляющие внутри волокна и вне.
Внутри волокна:
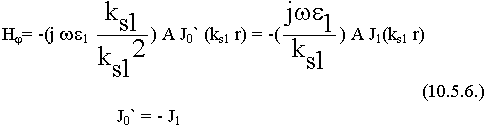
при дифференцировании

Вне волокна:
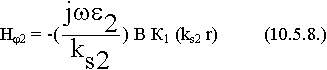
Используем непрерывность касательных составляющих:
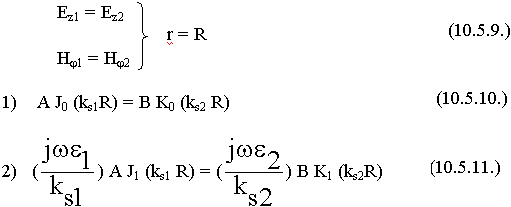
Разделим (10.5.10.) на (10.5.11.):
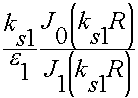 =
=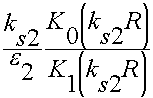 (10.5.12.)
(10.5.12.)
В явном виде такое уравнение решить нельзя. Оно трансцендентное, имеет большое множество решений, каждому из которых соответствует своя волна.
Простейшая волна Е01
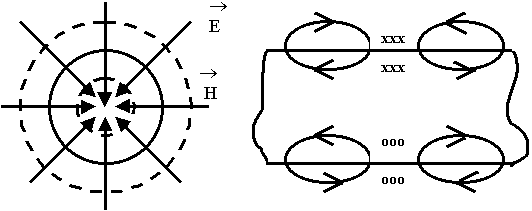
В отличие от волновода часть энергии выходит за пределы.
Возможность полевого электродинамического подхода позволяет рассчитать напряженность электрического и магнитного полей. Законы геометрической оптики позволяют определить углы.
Если ks2 = 0, то 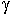 = k2=k0n2 - критический режим. Волна выходит в окружающее пространство.
= k2=k0n2 - критический режим. Волна выходит в окружающее пространство.  - продольное волновое число Vф = с.
- продольное волновое число Vф = с.
10.5.2. Несимметричные волны в оптическом волокне
Наряду с симметричными волнами, в волокне могут существовать и распространяться несимметричные волны.
В случае несимметричных волн, перенос энергии осуществляется гибридными волнами НЕ и ЕН. Для них (Еz  0 , Hz
0 , Hz  0). Гибридные волны являются основными волнами в оптических волокнах.
0). Гибридные волны являются основными волнами в оптических волокнах.
Основная волна НЕ11 - существует на всех частотах. Когда плоская волна распространяется вдоль волокна, она искажается.
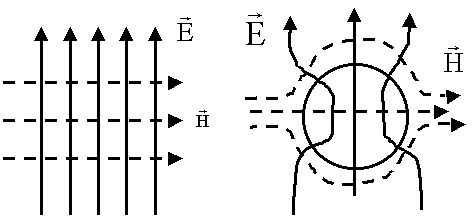
Часть энергии передается внутри стержня, часть вне. В стержне волна распространяется медленнее, чем в окружающем пространстве, за счет разности скоростей поле искажается и становится гибридным.
Все кабельные линии связи используют тип волны “Т”.
“Т” - волна. Еz = 0 Hz = 0. Из общего анализа “Т” волна возможна, когда ks = 0:
 кр =
кр = ![]() ;
;  кр
кр 
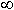
Волна “Т” существует на любых частотах.
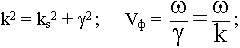 Vф не зависит от частоты.
Vф не зависит от частоты.
Дисперсия отсутствует в линиях передачи с волной типа “Т”.
11. Линии передачи с волной "Т"
11.1. Коаксиальная линии передачи Нz = 0 Ez = 0
В коаксиальной линии могут наряду с волной типа “Т” распространяется волны типа “E” и “H”, но здесь они являются высшими волнами и не рассматриваются.
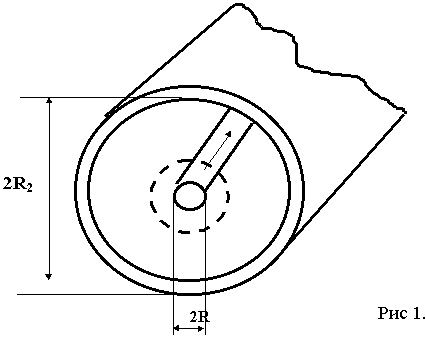
Продольные составляющие полей в волноводе возникают за счет явления многократного отражения от стенок волновода.
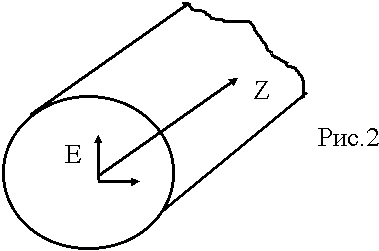
Введем в волновод плоскую электромагнитную волну (рис. 2). Неизбежно в этом случае появляется продольная составляющая поля за счет того, что поле Н замыкается само на себя (div H = 0).
При отсутствии продольных составляющих как электрические, так и магнитные поля расположены в плоскости поперечного сечения. Это можно сделать, если в линию передачи ввести еще один дополнительный проводник.
В волноводе волна типа “Т” не может распространяется.
Для расчета полей такой линии передачи воспользуемся законом полного тока. С этой целью выберем контур, охватывающий ток с радиусом r (см. рис. 1)
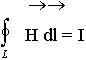
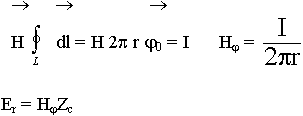
Все как в плоской электромагнитной волне.
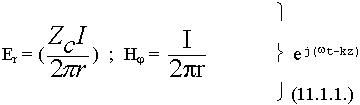
Поле волны Т в коаксиальной линии.

11.2. Оптимизация размеров в коаксиальной линии передачи
Целью оптимизации является создание кабеля, который имеет максимальную передаваемую мощность (например: кабель с минимальным затуханием, самый дешевый кабель и т.д.)
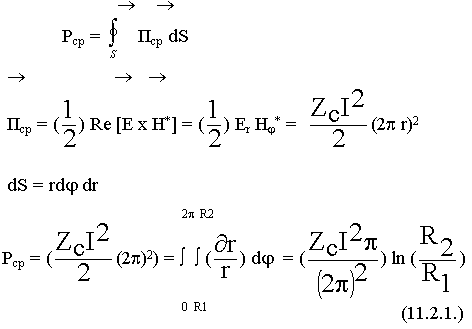
Ограничением уровня передаваемой мощности служит:
- Разогрев линии за счет того, что токи будут расти.
- Предельно-допустимое значение напряженности электрического поля.
Напряженность электрического поля больше всего вблизи центрального проводника:
Ermax = (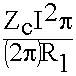 )
) 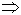 I = (
I = (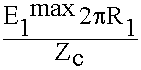 ) (11.2.2.)
) (11.2.2.)
Рассчитаем максимальную среднюю мощность:
Рсрmax = (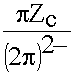 ) (
) (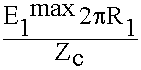 ) ln (
) ln (![]() ) = (
) = (![]() ) Ermax R12 ln (
) Ermax R12 ln (![]() )
)
(11.2.3.)
Для повышения передаваемой мощности, прежде всего, следует подумать как выбрать размеры.
Выделим функциональную зависимость от геометрических размеров:
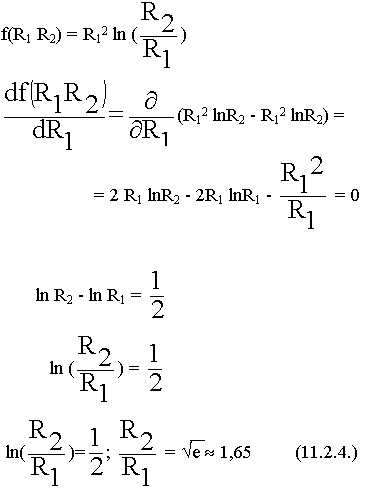
По такому же принципу можно решить и другие задачи оптимизации. Если надо передать сигнал с минимальными потерями, то (![]() )
) 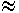 3,6
3,6
11.3. Другие типы линий передачи с волной Т
Двухпроводная линия
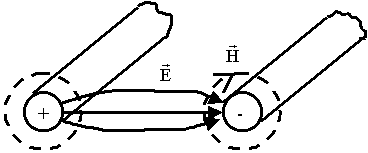
Несимметричные микрополосковые линии передачи широко используются для реализации печатных схем в диапазоне сверхвысоких частот.
12. Объемные резонаторы
12.1. Понятие объемного резонатора
Кратко вспомним, что изучили.
- Плоские волны в безграничном пространстве
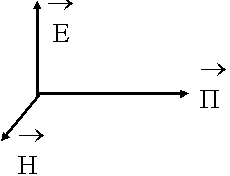
-
Граничные условия
-
Волновод

Что же будет, если волну вообще загнать в замкнутое пространство?
Переходим к изучению волновых процессов, ограниченных замкнутой металлической полостью, называемую объемным резонатором.
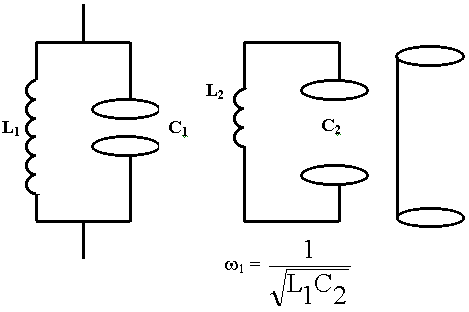
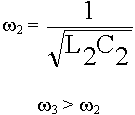
Уменьшаем L и C, в таком контуре добротность крайне низка, контур отдает свою энергию в окружающее пространство.
Что необходимо сделать для повышения добротности этого контура?
Попробуем вот так.
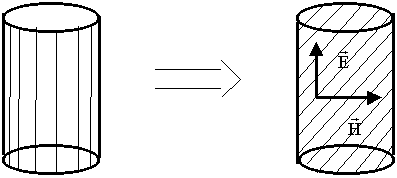
Излучение будет уменьшаться. В конце концов мы перейдем к замкнутой металлической полости. Это есть объемный резонатор.
На резонансной частоте происходит эффективный обмен энергиями электрического и магнитного полей.
А где найти конденсатор и катушку в этой коробке?
В каждой точке резонатора имеются электрические и магнитные поля и обмен между ними происходит в каждой точке.
Добротность собственная объемного резонатора оказалась много больше, чем у колебательного контура.
Q0 конт = 100 ¸ 300
Q0 объем.рез = 10000 ¸ 50000
Объемный резонатор в радиорелейной аппаратуре выполняет функцию колебательного контура - высокодобротного элемента.
12.2. Условие резонанса в объемном резонаторе
Это условие справедливо для случая, когда резонатор выполнен из отрезков
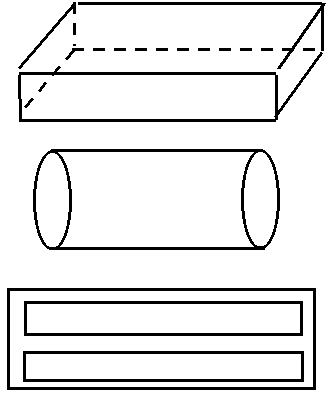
Установим связь между геометрическими размерами и резонансной частотой. Пусть имеется некоторая произвольная линия передачи с вектором магнитной волны.
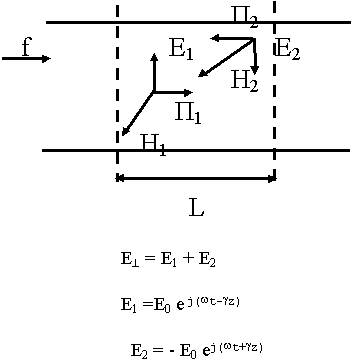
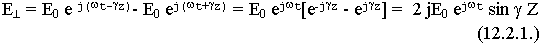
На торцевых поверхностях 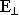 = 0 при Z = 0 ; Z = L
= 0 при Z = 0 ; Z = L
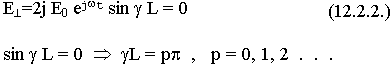
р - количество вариаций поля по длине резонатора.
Для 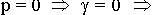 в резонаторе поле отсутствует такая структура для Ez
в резонаторе поле отсутствует такая структура для Ez  0, распространяется волна Е типа.
0, распространяется волна Е типа.

Для того, чтобы выполнялись граничные условия, L должна быть строго определенной.
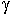 =
= ![]() ;
;  =
= ![]()
 длина волны в волноводе.
длина волны в волноводе.
![]() =
= ![]()
 L = p (
L = p (![]() )
)
Lрез = p (![]() ) (12.2.3.)
) (12.2.3.)
Для любых линий передачи:
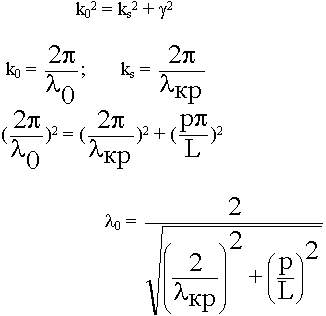
 0 - резонансная длина волны:
0 - резонансная длина волны:
fрез = ![]() (12.2.4.)
(12.2.4.)
12.3. Основные типы объемных резонаторов
12.3.1. Прямоугольный резонатор
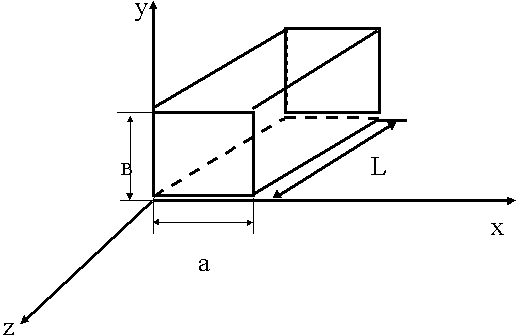
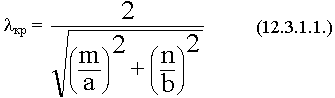
Для волн типа Н индексы m или n могут обращаться в 0. Для Е волн индексы m и n  0.
0.
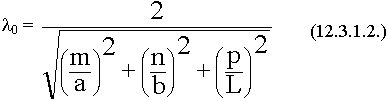
Индексам m и n соответствует своя структура поля. Введем обозначения Нmnp и Еmnp, р - показывает число полуволн укладывающихся вдоль длины резонатора.
m,n - число полуволн, укладывающихся вдоль ширины и высоты резонатора соответственно.
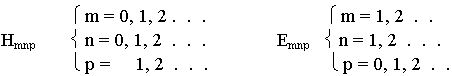
Для каждого типа волны - своя резонансная частота. Для получения минимальной резонансной частоты fрез надо использовать колебания с минимальными значениями m, n, p.
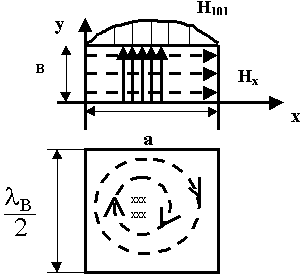
12.3.2. Цилиндрический резонатор
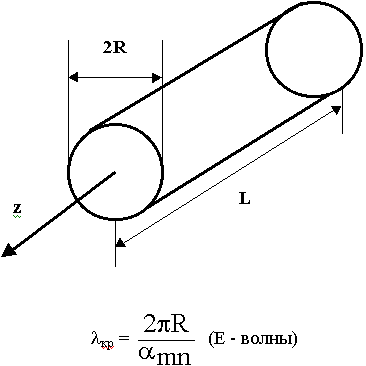
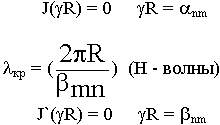
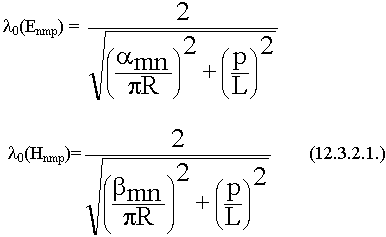
Основные колебания Н111 и Е010
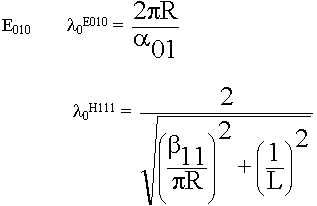
Может оказаться, что колебания имеют одну и туже резонансную частоту, это называется вырождением колебаний.
 0E010 =
0E010 =  0H111
0H111
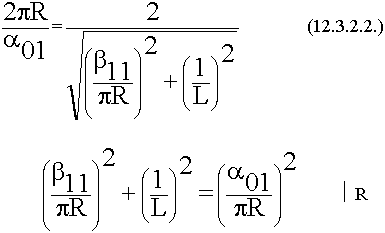
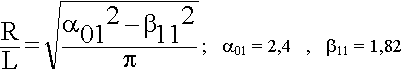
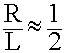
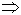 когда D
когда D  L, то наблюдается вырождение, если D > L, то
L, то наблюдается вырождение, если D > L, то  >
> 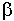
 резЕ010 <
резЕ010 <  резН111. Это означает, что Е010 - основное колебание. Если D < L, то
резН111. Это означает, что Е010 - основное колебание. Если D < L, то  <
< 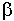 ,
,  резЕ010 >
резЕ010 >  резН111 Н111 - основное колебание.
резН111 Н111 - основное колебание.

n - число вариаций поля по 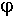 вдоль азимута.
вдоль азимута.
m - число вариаций по радиусу, порядковый номер функции Бесселя.
р - число вариаций поля по длине.
12.4. Собственная добротность ОР
В ОР за счет энергии внешнего источника (генератора) происходит накопление электромагнитной энергии. Наряду с накоплением энергии в ОР происходят процессы расхода энергии.
- На разогрев стенок резонатора - за счет преобразования поверхностных токов в тепловую энергию.
- Часть энергии расходуется из-за неидеальности резонатора (диэлектрические потери).
- Если в стенках резонатора имеются щели, то энергия выходит через них (излучение).
Собственная добротность - это отношение накопленной в резонаторе энергии к энергии рассеиваемой этим резонатором за 1 период:
Q0 = 2
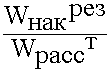 (12.4.1.)
(12.4.1.)
Выясним, от каких факторов зависит собственная добротность резонатора. Вся энергия заключена либо в электрическом, либо в магнитном поле.
Wmax Emax H = 0
Wmax Hmax E = 0
На резонансной частоте:
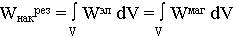
Найдем Wнакр и Wтрасс.рез:
Из теоремы Пойнтинга
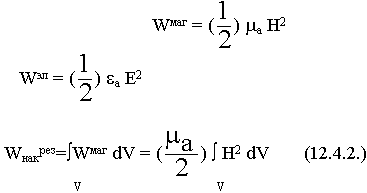
Энергия накопленная пропорциональна объему ( 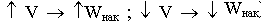 )
)
Потери энергии :
- Потери за счет токов.
- Потери в среде, заполняющей объемный резонатор (диэлектрические потери).
- Потери на излучение, если есть щели, трещины.
Учтем только потери за счет поверхностных токов в стенках резонатора:
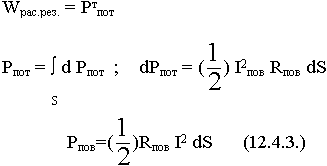
Поверхностные токи определяются магнитным полем:
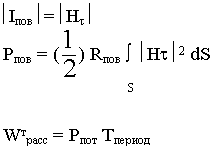
Получаем:
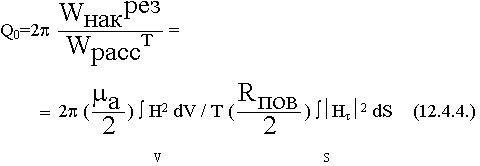
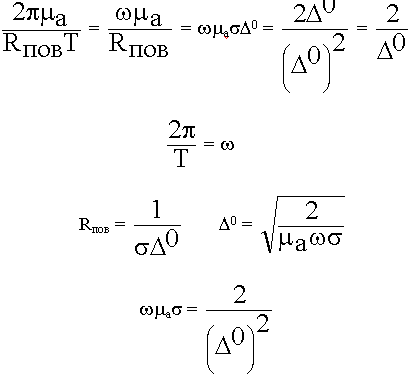
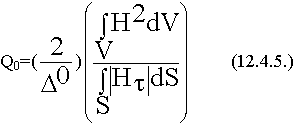
Выводы:
- Cобственная Q0 зависит от свойств материала, т.е. зависит от проводимости, чем больше проводимость, тем больше Q0. Объемные резонаторы покрывают серебром (слой серебра
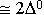 , очень тонкий слой).
, очень тонкий слой). 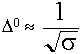 .
. - Величина Q0 зависит от структуры поля в резонаторе, т.е. от типа колебаний в резонаторе. Для разных типов колебаний Q0 различна. Предположим, что магнитные поля в резонаторе всюду одинаковы
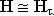 .
.
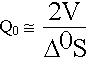
С объемом (V) связано накопление энергии, с поверхностью (S) связано рассеивание энергии. Глубина проникновения 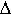 0 связана с материалом. Q0 зависит от геометрических размеров (V и S). Увеличение V приводит к возникновению других типов. Q0 очень зависит от качества обработки внутренней поверхности резонатора (внутреннюю поверхность полируют)
0 связана с материалом. Q0 зависит от геометрических размеров (V и S). Увеличение V приводит к возникновению других типов. Q0 очень зависит от качества обработки внутренней поверхности резонатора (внутреннюю поверхность полируют)
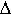 0 в СВЧ: 10-5
0 в СВЧ: 10-5 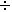 10-6 М (очень мала)
10-6 М (очень мала)
размеры резонаторов пропорциональны длине волны:
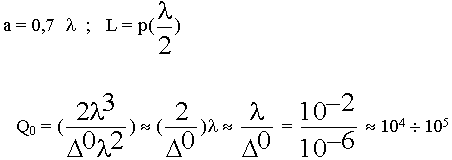
Сравнение Q0 от формы резонатора:
1) Прямоугольный резонатор в = ![]()
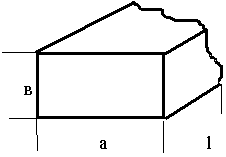
2) Квадратный резонатор
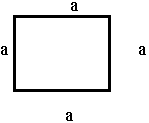
3) Круглый резонатор r = ![]()
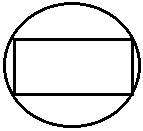
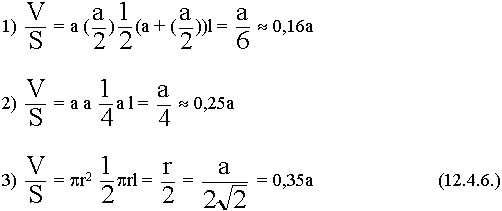
12.4.1. Нагруженная и внешняя добротности
На практике имеем:
Нагруженная добротность - это отношение накопленной в резонаторе энергии к энергии рассеянной в резонаторе и в нагрузке за 1 период.
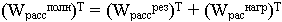
Рассмотрим величину ![]() с целью выяснения связи между Q0 и Qн, Qвн:
с целью выяснения связи между Q0 и Qн, Qвн:
![]() =
= 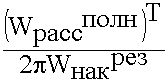 =
= 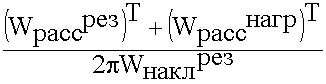
Qвн = 2p 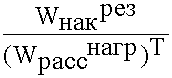 - характеризует связь резонатора с нагрузкой
- характеризует связь резонатора с нагрузкой
![]() =
= ![]() +
+ 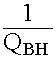 (12.4.7.)
(12.4.7.)
12.5. Режим связи резонатора с нагрузкой
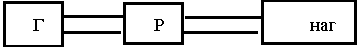
По степени связи резонатора с нагрузкой различают 3 режима работы:
1) Режим критической связи (критический режим).
Q0 = Qвн это означает, что энергия рассеяния в нагрузке равна энергии, потерянной в резонаторе.
(Wрассрез)Т = (Wрасснагр)Т
2) Режим пересвязи (сильная связь)
Q0 > Qвн (Wрассрез)Т < (Wрасснагр)Т
Вся энергия теряется на нагрузке.
3) Режим недосвязи (слабая связь)
Q0 < Qвн Большая часть энергии теряется в резонаторе. (Wрасрез)Т > (Wраснаг)Т
12.6. Измерение добротности
Qн = fрез / 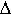 f / на уровне 3 дБ
f / на уровне 3 дБ
 , дБ = 20 lg (
, дБ = 20 lg (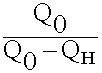 ) (12.6.1.)
) (12.6.1.)
12.7. КПД объемного резонатора
 =
= 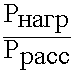
Отношение мощности, поступающей в нагрузку к мощности, рассеиваемой в резонаторе и нагрузке.
Рнагр 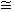
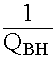 Ррасс =
Ррасс = ![]()
 =
= 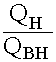 = Qн ((
= Qн ((![]() ) - (
) - (![]() ))
))
 = 1 - (
= 1 - (![]() ) (12.7.1.)
) (12.7.1.)
Пример:
Q0 = 2000
 = 1 - (
= 1 - (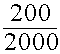 ) = 0,9
) = 0,9
Qн = 200
Список литературы
Основная
1. Вольман В.И., Пименов Ю.В. Техническая электродинамика. – М.: Связь, 1971.
2. Семенов Н.А. Техническая электродинамика. – М.: Связь, 1973.
3. Фальковский О.И. Техническая электродинамика. – М.: Связь, 1978.
4. Андрусевич Л.К., Беленький В.Г. Основы электродинамики. Новосибирск, СибГУТИ, 2000.
Дополнительная
Красюк Н.П., Дымович Н.Д. Электродинамика и распространение радиоволн. – М.: Высшая школа, 1974.
Федоров Н.Н. основы электродинамики. – М.: Высшая школа, 1980.
Никольский В.В., Никольская Т.Н. Электродинамика и РРВ. – М.: Высшая школа, 1973.
Вайнштейн Л.А. Электромагнитные волны, М.: Советское радио, 1957.
Гольдштейн А.Д., Зернов Н.В. Электромагнитные поля и волны. – М.: Советское радио, 1971.
Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся вузов, - М.: Наука, 1976.
Брунов В.Н., Гольдберг Л.Н., Кляцкин Н.Г., Цейтлин Л.А. Теория электромагнитного поля. – М.: Госэнергоиздат, 1962.
Методические указания к лабораторным работам. Новосибирск, СибГУТИ, 1999.