1.1. Обобщённая структурная схема радиотехнической информационной системы
1.3. Динамическое представление сигналов
1.1. Обобщённая структурная схема радиотехнической информационной системы
Научно-технический прогресс в различных областях общественной жизни сопровождается резким увеличением потоков передаваемой и принимаемой информации. Основную роль в решении проблемы повышения эффективности передачи информации играют радиотехнические информационные системы (РТИС), к которым относятся системы радиосвязи, телевидения, радиолокации, радионавигации, радиотелеметрии и многие другие. Несмотря на различия, обусловленные целевым назначением, перечисленные системы характеризуются общими чертами, позволяющими изучать их с общих позиций. В связи с этим рассмотрим обобщённую структурную схему РТИС, представленную на рис. 1.1.
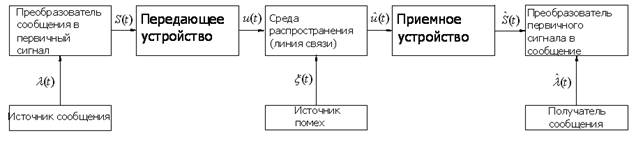
Рис. 1.1
В состав РТИС входят:
¾ источник сообщений;
¾ преобразователь сообщений в первичный сигнал;
¾ передающее устройство;
¾ линия связи;
¾ приёмное устройство;
¾ преобразователь первичного сигнала в сообщение;
¾ получатель сообщения.
Помимо этого в структурной схеме РТИС фигурирует источник помех.
Источник сообщений формирует сообщение λ(t), подлежащее передаче. В качестве сообщений могут выступать речевое сообщение, изображение какого-либо объекта, температура или давление в узлах летательного аппарата и т.д. Поскольку сообщения отображаются в процессах различной физической природы (изменение давления, температуры, интенсивности светового потока и др.), эти процессы при передаче по РТИС необходимо преобразовать в электрические сигналы. Эту задачу решает преобразователь сообщения λ(t) в первичный электрический сигнал s(t). Операцию такого преобразования можно описать символическим выражением
s(t)=Wcnc [λ(t)], (1.1)
где Wcnc – оператор (правило) преобразования сообщения в первичный сигнал.
В подавляющем большинстве случаев энергия первичного сигнала сосредоточена в низкочастотной области. При передаче сообщений по РТИС энергия сигнала должна располагаться в области радиодиапазона. Операцию преобразования первичного сигнала s(t) в радиосигнал u(t) осуществляет передающее устройство в соответствии с выражением
u(t)= Wcnc [s(t)], (1.2)
где Wcnc – оператор преобразования первичного сигнала в радиосигнал.
Перенос первичного сигнала в соответствующий радиодиапазон на практике осуществляется при помощи операции модуляции, т.е. изменения одного из параметров высокочастотного колебания соответствующего радиодиапазона в соответствии с изменением s(t). Поэтому сигнал s(t) называют управляющим (модулирующим), а сигнал u(t) - модулированным сигналами.
Радиосигналы u(t) распространяются по линии связи, в качестве которой могут выступать: свободное пространство, кабельные, оптические, волноводные и другие линии. В линии связи действуют помехи ξ(t), искажающие сигнал û(t). Передачу сигнала по линии связи в операторной форме можно записать следующим образом:
û(t)=Wлс[û(t)∙ξ(t)]. (1.3)
Приёмное устройство осуществляет обратную операцию преобразования радиосигнала û(t) в первичный сигнал ŝ(t), который также будет отличаться от исходного сигнала s(t), т.е.
ŝ(t)=Wпрм[û(t)]. (1.4)
где Wпрм – оператор преобразования сигнала приёмным устройством.
И, наконец, преобразователь первичного сигнала û(t) в сообщениe λ(t):
λ(t)= Wпcc[ŝ(t)] (1.5)
осуществляет преобразование ŝ(t) в форму, удобную для восприятия сообщения получателем. Здесь Wпcc – оператор преобразования первичного сигнала в сообщение.
Таким образом, передача сообщений в РТИС характеризуется цепочкой преобразований различных сигналов различными радиотехническими устройствами.
Принципы и методы формирования и преобразования электрических сигналов и электромагнитных волн радиодиапазона и их использование для передачи информации составляют предмет теоретической радиотехники. Исходя из этого, можно выделить две основные задачи, решаемые радиотехникой.
Первой задачей является изучение различных видов сигналов, их свойств и характеристик с целью их использования в радиотехнических системах. Эту задачу решает теория радиотехнических сигналов.
Процесс передачи сообщений в радиотехнической информационной системе, как подчёркивалось выше, состоит в последовательности преобразований сигналов, которые осуществляются посредством соответствующих физических устройств – радиотехнических цепей. Поэтому, второй задачей радиотехники является изучение и практическое использование принципов и методов преобразования сигналов в различных цепях. Эту задачу решает теория радиотехнических цепей.
1.2. Классификация сигналов
В настоящее время практическая радиотехника использует множество различных сигналов. Прежде, чем приступать к их изучению, необходимо определить понятие «сигнал» и охарактеризовать его общие свойства.
Назовём сигналом изменяющуюся физическую величину, отображающую передаваемое сообщение. В качестве таких величин могут выступать ток, напряжение, электромагнитное поле, световой поток и др. Иными словами, сигнал выступает как материальный носитель информации.
При теоретических исследованиях используют математические модели сигналов. В самом общем виде математическая модель сигнала представляет собой функцию ![]() аргумента времени
аргумента времени ![]() . Следует отметить, что математическая модель не учитывает конкретную физическую природу сигнала. Одной и той же математической моделью может быть описано изменение во времени и напряжения, и интенсивности светового потока, и напряжённости электромагнитного поля.
. Следует отметить, что математическая модель не учитывает конкретную физическую природу сигнала. Одной и той же математической моделью может быть описано изменение во времени и напряжения, и интенсивности светового потока, и напряжённости электромагнитного поля.
Все сигналы как физические процессы являются материальными и описываются вещественными функциями. Вместе с тем, при теоретических исследованиях часто удобно описывать сигналы комплексными функциями.
Вид функции ![]() определяет форму сигнала.
определяет форму сигнала.
Как функция времени сигнал может быть определён как на конечном, так и на бесконечном интервале времени. Реальные сигналы всегда конечны. Если сигнал ![]() определён на интервале
определён на интервале ![]() , то величина
, то величина ![]() называется длительностью сигнала. Такие сигналы получили название финитных сигналов. При теоретическом анализе сигнал может быть определён как на бесконечном
называется длительностью сигнала. Такие сигналы получили название финитных сигналов. При теоретическом анализе сигнал может быть определён как на бесконечном ![]() , так и на полубесконечном
, так и на полубесконечном ![]() интервале времени.
интервале времени.
Т.к. сигнал является материальным носителем информации, он обладает энергетическими характеристиками. К основным энергетическим характеристикам относится энергия сигнала
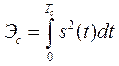 , (1.6)
, (1.6)
и средняя мощность
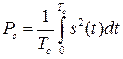 . (1.7)
. (1.7)
Отметим, что если ![]() представляет собой изменение напряжения во времени, энергия сигнала, выделяемая при нагрузке в 1 Ом имеет размерность
представляет собой изменение напряжения во времени, энергия сигнала, выделяемая при нагрузке в 1 Ом имеет размерность ![]() , а средняя мощность в
, а средняя мощность в ![]() .
.
Таким образом, в общем случае сигнал характеризуется формой, длительностью, энергией и средней мощностью.
Изменение сигнала во времени может происходить неслучайным (детерминированным), либо случайным образом. В соответствии с этим сигналы подразделяются на детерминированные и случайные.
К детерминированным сигналам относятся сигналы, значения которых в любой момент времени ![]() полностью известны. Детерминированным сигналом, например, является гармоническое колебание с постоянными на интервале
полностью известны. Детерминированным сигналом, например, является гармоническое колебание с постоянными на интервале ![]() амплитудой, частотой и начальной фазой. Детерминированные сигналы не переносят информации и являются вспомогательными при различных преобразованиях сигналов. С другой стороны, детерминированные сигналы являются удобной моделью при анализе радиотехнических систем.
амплитудой, частотой и начальной фазой. Детерминированные сигналы не переносят информации и являются вспомогательными при различных преобразованиях сигналов. С другой стороны, детерминированные сигналы являются удобной моделью при анализе радиотехнических систем.
Случайные сигналы – это сигналы, значения которых в любой момент времени точно предсказать невозможно. Математическими моделями случайных сигналов являются случайные процессы. Собственно говоря, информация содержится в случайных изменениях физических величин. С другой стороны, моделями случайных процессов описываются и помехи в линии связи. Всё это определяет важность изучения случайных сигналов.
Сигнал ![]() , как уже подчёркивалось выше, представляет собой изменяющуюся во времени величину и с этой точки зрения характеризуется множеством
, как уже подчёркивалось выше, представляет собой изменяющуюся во времени величину и с этой точки зрения характеризуется множеством ![]() значений и множеством моментов времени
значений и множеством моментов времени ![]() , которые она может принимать эти значения. Как множество
, которые она может принимать эти значения. Как множество ![]() , так и множество
, так и множество ![]() может быть непрерывным (континуальным) или дискретным (счётным). Положим эти два признака в основу классификации сигналов.
может быть непрерывным (континуальным) или дискретным (счётным). Положим эти два признака в основу классификации сигналов.
На рис. 1.2 представлены графики изменения величины ![]() в зависимости от моментов времени
в зависимости от моментов времени ![]() в координатах
в координатах ![]()
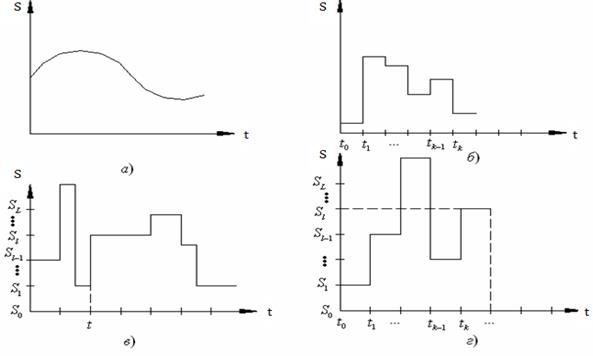
Рис. 1.2
Если множества ![]() и
и ![]() являются непрерывными множествами, т.е. в любой момент времени
являются непрерывными множествами, т.е. в любой момент времени ![]() сигнал может принимать любое значение из множества
сигнал может принимать любое значение из множества ![]() , то такие сигналы называют аналоговыми (непрерывными) сигналами (рис. 1.2, а). Аналоговые сигналы имеют место на выходе микрофона, датчика температуры или давления и т.д.
, то такие сигналы называют аналоговыми (непрерывными) сигналами (рис. 1.2, а). Аналоговые сигналы имеют место на выходе микрофона, датчика температуры или давления и т.д.
Если множество ![]() непрерывно, а множество
непрерывно, а множество ![]() дискретно, т.е. сигнал может принимать любое значение из множества
дискретно, т.е. сигнал может принимать любое значение из множества ![]() но в строго фиксированные моменты времени
но в строго фиксированные моменты времени ![]() , или
, или ![]() , то такие сигналы называются дискретными (рис 1.2, б). Здесь черта обозначает, что
, то такие сигналы называются дискретными (рис 1.2, б). Здесь черта обозначает, что ![]() принимает значения от
принимает значения от ![]() до
до ![]() . Примером дискретного сигнала может служить отражённый от цели сигнал на входе приёмника радиолокационной станции. Действительно, моменты времени
. Примером дискретного сигнала может служить отражённый от цели сигнал на входе приёмника радиолокационной станции. Действительно, моменты времени ![]() определяются временем оборота антенны, а значения
определяются временем оборота антенны, а значения ![]() сигнал может принимать любые, т.к. цель может иметь произвольное положение в пространстве.
сигнал может принимать любые, т.к. цель может иметь произвольное положение в пространстве.
Если множество значений ![]() дискретно, а множество моментов времени
дискретно, а множество моментов времени ![]() непрерывно, т.е. сигнал принимает строго фиксированные значения
непрерывно, т.е. сигнал принимает строго фиксированные значения ![]() в любой произвольный момент времени
в любой произвольный момент времени ![]() , или
, или ![]() , то такие сигналы называются квантованными (рис. 1.2, в). К квантованным сигналам можно отнести сигнал на выходе контролёра-автомата метрополитена. Число пассажиров, которые проходят через контролёр - автомат всегда принимает целые значения, а значения моментов времени произвольные.
, то такие сигналы называются квантованными (рис. 1.2, в). К квантованным сигналам можно отнести сигнал на выходе контролёра-автомата метрополитена. Число пассажиров, которые проходят через контролёр - автомат всегда принимает целые значения, а значения моментов времени произвольные.
И, наконец, если множества ![]() и
и ![]() дискретны, то такие сигналы
дискретны, то такие сигналы ![]() называются цифровыми (рис. 1.2, г). Своё название такие сигналы получили ввиду того, что значения
называются цифровыми (рис. 1.2, г). Своё название такие сигналы получили ввиду того, что значения ![]() сигнала и моменты
сигнала и моменты ![]() времени изменений значений могут быть представлены числами натурального ряда. Примерами цифровых сигналов могут служить сигналы, которыми обмениваются устройства ЭВМ, сигналы телексной связи и другие.
времени изменений значений могут быть представлены числами натурального ряда. Примерами цифровых сигналов могут служить сигналы, которыми обмениваются устройства ЭВМ, сигналы телексной связи и другие.
Отметим, что в дискретном и цифровом сигналах значения ![]() сохраняются в течение интервала времени
сохраняются в течение интервала времени ![]() неизменным. Если значения сигнала фиксировать в моменты времени
неизменным. Если значения сигнала фиксировать в моменты времени ![]() короткими импульсами
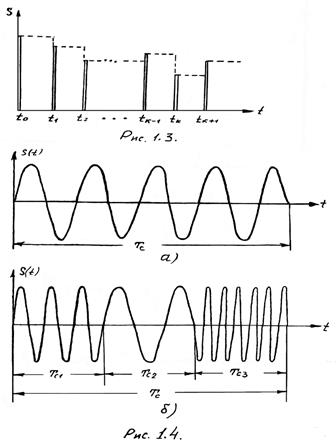
короткими импульсами ![]() , то такие сигналы называются импульсными (рис. 1.3).
, то такие сигналы называются импульсными (рис. 1.3).
Для сравнений на рисунке пунктирными линиями показан дискретный сигнал, соответствующий импульсному сигналу. В ряде случаев значения импульсного сигнала называют отсчётами.
Продолжим классификацию сигналов. Если на интервале времени ![]() сигнал описывается одной элементарной функцией времени, то такой сигнал называется простым (элементарным) сигналом (рис. 1.4,а).
сигнал описывается одной элементарной функцией времени, то такой сигнал называется простым (элементарным) сигналом (рис. 1.4,а).
Если же на этом интервале времени сигнал описывается совокупностью простых сигналов, например,
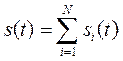 ,
,
где ![]() имеет длительность
имеет длительность ![]() , то такие сигналы называют составными (или сложными).
, то такие сигналы называют составными (или сложными).
На рис. 1.4, б изображён составной сигнал, образованный совокупностью трёх простых сигналов описываемых гармоническими функциями.
И, наконец, в связи с широким использованием цифровых сигналов в современных РТИС, остановимся на понятии ансамбля сигналов. Ввиду того, что в цифровых РТИС число значений первичных сигналов ![]() ограничено, для их передачи можно использовать конечное число сигналов
ограничено, для их передачи можно использовать конечное число сигналов ![]() . Совокупность таких сигналов образуют ансамбль сигналов. Важнейшей характеристикой ансамбля сигналов является его объем
. Совокупность таких сигналов образуют ансамбль сигналов. Важнейшей характеристикой ансамбля сигналов является его объем ![]() , т.е. число сигналов, входящих в ансамбль. От этого показателя зависит информативность каждого сигнала в отдельности и ансамбля в целом, способность противостоять помехам, время доведения сообщений до получателя т.е. все то, что определяет эффективность радиотехнической информационной системы.
, т.е. число сигналов, входящих в ансамбль. От этого показателя зависит информативность каждого сигнала в отдельности и ансамбля в целом, способность противостоять помехам, время доведения сообщений до получателя т.е. все то, что определяет эффективность радиотехнической информационной системы.
И в заключение отметим, что понятие ансамбля сигналов может быть распространенно и на совокупность ансамбля сигналов.
1.3. Динамическое представление сигналов
При построении РТИС возникают задачи анализа и синтеза радиотехнических сигналов. Сущность анализа состоит в том, что изучаемый объект разбивается на составные части, после чего проводится их исследование. Применительно к радиотехническим сигналам при анализе исследуемый сигнал описывается совокупностью других более простых сигналов с хорошо изученными свойствами. Такое представление позволяет, с одной стороны, сложную задачу преобразования исследуемого сигнала радиотехническими устройствами свести к задачам преобразования известных сигналов, а с другой стороны, - достаточно эффективно решать задачи синтеза сигналов с заданными свойствами.
Как уже подчеркивалось выше, в общем случае сигнал ![]() описывается функцией времени, позволяющей рассматривать сигнал как процесс, развивающейся во времени. Поэтому представление сигнала
описывается функцией времени, позволяющей рассматривать сигнал как процесс, развивающейся во времени. Поэтому представление сигнала ![]() сложной формы совокупностью простых сигналов, также описываемых функциями времени, получило название динамического или временного представления.
сложной формы совокупностью простых сигналов, также описываемых функциями времени, получило название динамического или временного представления.
В теории радиотехнических сигналов для динамического представления используются следующие элементарные функции: функция знака ![]() (сигнум-функция), единичная функция
(сигнум-функция), единичная функция ![]() (функция включения, функция Хевисайда), дельта-функция
(функция включения, функция Хевисайда), дельта-функция ![]() (функция Дирака) и прямоугольный импульс с единичной высотой
(функция Дирака) и прямоугольный импульс с единичной высотой ![]() (рис. 1.5, а, б, в, г). Рассмотрим вид этих функций и способы представления радиотехнических сигналов этими функциями.
(рис. 1.5, а, б, в, г). Рассмотрим вид этих функций и способы представления радиотехнических сигналов этими функциями.
Функция знака ![]() имеет постоянную величину, равную единице, знак которой изменяется скачком при переходе переменной
имеет постоянную величину, равную единице, знак которой изменяется скачком при переходе переменной ![]() через ноль (рис. 1.5, а). Математически функция знака описывается выражением
через ноль (рис. 1.5, а). Математически функция знака описывается выражением
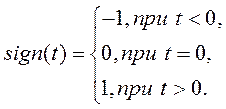 (1.8)
(1.8)
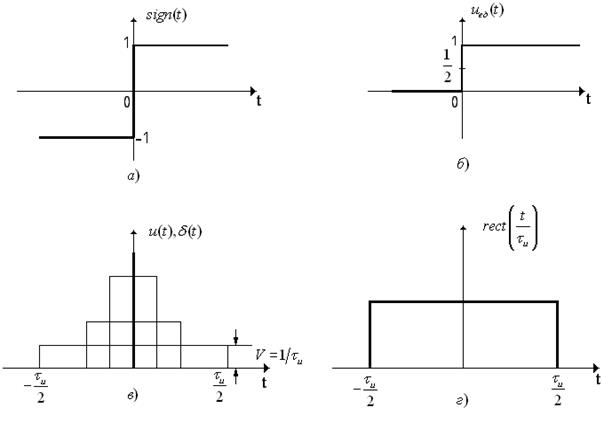
Рис. 1.5
Умножение ![]() на
на ![]() означает изменение знака сигнала в момент времени
означает изменение знака сигнала в момент времени ![]() .
.
Единичная функция ![]() характеризует собой единичный скачок при переходе
характеризует собой единичный скачок при переходе ![]() через ноль (рис.1.5, б). Математическое выражение единичной функции имеет следующий вид
через ноль (рис.1.5, б). Математическое выражение единичной функции имеет следующий вид
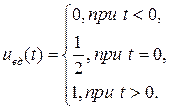 (1.9)
(1.9)
Умножение ![]() на
на ![]() равносильно включению этого сигнала в момент времени
равносильно включению этого сигнала в момент времени ![]() . Сравнивая (1.8) и (1.9) можно установить, что
. Сравнивая (1.8) и (1.9) можно установить, что
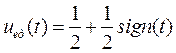 .
.
Дельта-функция ![]() была введена физиком-теоретиком П. Дираком. Рассмотрим импульс
была введена физиком-теоретиком П. Дираком. Рассмотрим импульс ![]() единичной площади и длительностью
единичной площади и длительностью ![]() (рис. 1.5, в)
(рис. 1.5, в)
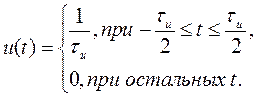
Будем уменьшать длительность импульса при сохранении его площади, равной единице. При этом высота импульса ![]() будет возрастать. При
будет возрастать. При ![]() высота импульса будет стремиться к бесконечности. Это и есть
высота импульса будет стремиться к бесконечности. Это и есть ![]() - функция (на рисунке выделена утолщенным отрезком со стрелкой)
- функция (на рисунке выделена утолщенным отрезком со стрелкой)
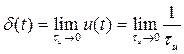 .
.
Математически ![]() -функция записывается следующим образом
-функция записывается следующим образом
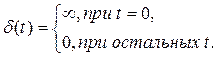 (1.10)
(1.10)
Сравнивая (1.9) и (1.10) нетрудно установить, что
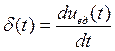 (1.11)
(1.11)
Отметим некоторые свойства ![]() - функции.
- функции.
Так как исходный импульс ![]() описывается четной функцией, то
описывается четной функцией, то ![]() - функция тоже четная, т.е.
- функция тоже четная, т.е.
![]()
Во-вторых, ввиду того, что площадь исходного импульса равна единице, т.е.
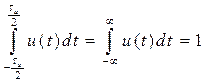 ,
,
поэтому 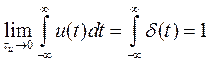 .
.
И наконец, отметим фильтрующее свойство ![]() - функции
- функции
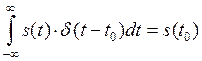 . (1.12)
. (1.12)
Иными словами интеграл произведения ![]() на
на ![]() равен значению
равен значению ![]() в момент времени
в момент времени ![]() .
.
Прямоугольный импульс с единичной амплитудой (рис. 1.5, г) описывается следующим выражением
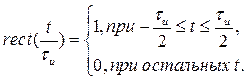 (1.13)
(1.13)
С помощью прямоугольного импульса с единичной высотой можно достаточно просто описать периодическую последовательность прямоугольных импульсов, цифровые сигналы в виде двоичных кодовых комбинаций и другие.
Рассмотрим теперь каким же образом сигнал произвольной формы ![]() можно описать с помощью рассмотренных выше элементарных функций. На практике для такого представления используются единичная функция и
можно описать с помощью рассмотренных выше элементарных функций. На практике для такого представления используются единичная функция и ![]() - функция.
- функция.
Возьмем сигнал произвольной формы ![]() и приближенно представим его ступенчатой функцией, которая изменяется в моменты времени
и приближенно представим его ступенчатой функцией, которая изменяется в моменты времени ![]() , отстоящие друг от друга на равные интервалы времени
, отстоящие друг от друга на равные интервалы времени ![]() (рис. 1.6).
(рис. 1.6).
Пусть в момент времени ![]() сигнал принимает значение
сигнал принимает значение ![]() . Тогда на интервале времени
. Тогда на интервале времени ![]() значение сигнала можно представить в виде произведения
значение сигнала можно представить в виде произведения
![]()
Рассмотрим интервал времени ![]() . Значение сигнала в мо-мент времени
. Значение сигнала в мо-мент времени ![]() очевидно равно
очевидно равно ![]() , где
, где ![]() .
.
С другой стороны, величину ![]() можно представить в виде произведения
можно представить в виде произведения
![]() .
.
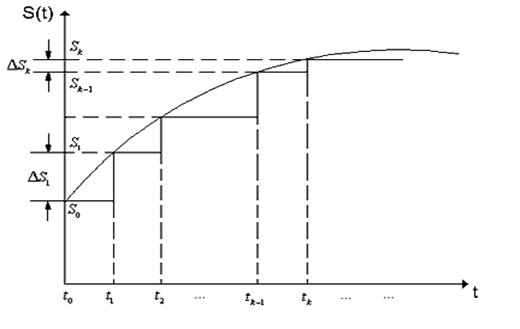
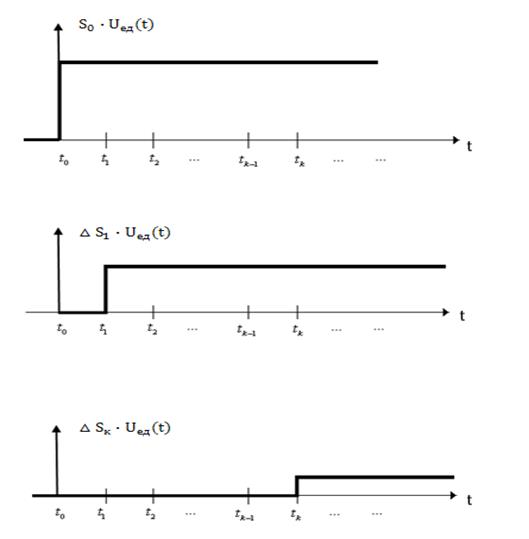
Рис. 1.6
Тогда значение сигнала в момент времени ![]() запишется следующим образом
запишется следующим образом
![]() .
.
Продолжая аналогичные рассуждения, получим
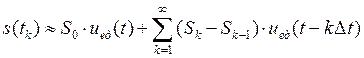 . (1.14)
. (1.14)
Очевидно, с уменьшением ![]() точность представления сигнала возрастает.
точность представления сигнала возрастает.
Если разделить обе части равенства (1.14) на ![]() и устремить
и устремить ![]() , можно получить точное выражение сигнала при его представлении совокупностью единичных функций
, можно получить точное выражение сигнала при его представлении совокупностью единичных функций
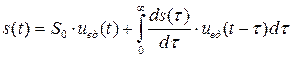 . (1.15)
. (1.15)
Перейдем к рассмотрению представления сигнала ![]() посредством
посредством ![]() - функции. Для этого представим сигнал в виде суммы прямоугольных импульсов длительностью
- функции. Для этого представим сигнал в виде суммы прямоугольных импульсов длительностью ![]() и высотой
и высотой ![]() (рис. 1.7).
(рис. 1.7).
Рассмотрим интервал времени ![]() . Очевидно, импульс на этом интервале времени можно представить следующим образом:
. Очевидно, импульс на этом интервале времени можно представить следующим образом:
![]() .
.
На произвольном интервале времени ![]() импульс:
импульс:
![]() .
.
Тогда сигнал, представленный в виде суммы прямоугольных импульсов, приближенно можно описать следующим выражением:
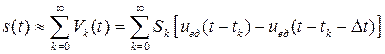 . (1.16)
. (1.16)
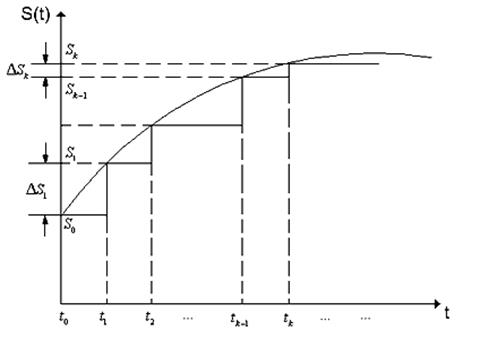
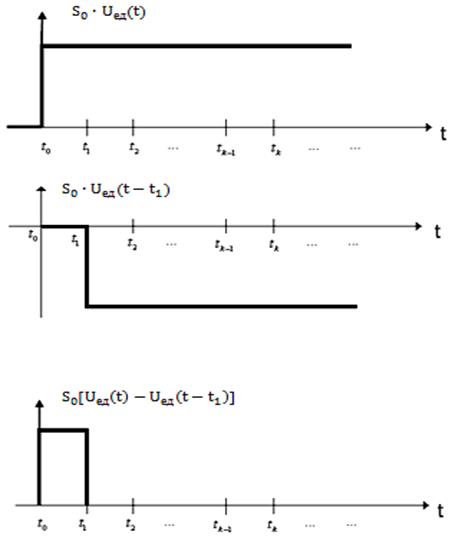
Рис. 1.7
Так же, как и в предыдущем случае, сигнал ![]() будет представлен тем точнее, чем меньше длительность импульсов
будет представлен тем точнее, чем меньше длительность импульсов ![]() . Разделив и умножив правую часть (1.16) на
. Разделив и умножив правую часть (1.16) на ![]() , получим
, получим
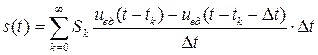 . (1.17)
. (1.17)
Устремим ![]() к нулю. Тогда суммирование в (1.17) можно заменить интегрированием по новой переменной
к нулю. Тогда суммирование в (1.17) можно заменить интегрированием по новой переменной ![]() , дифференциал которой
, дифференциал которой ![]() будет соответствовать
будет соответствовать ![]() .
.
Поскольку
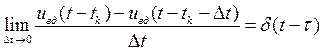 ,
,
выражение (1.17) примет следующий вид
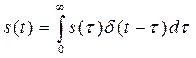 . (1.18)
. (1.18)
Распространяя область определений сигнала на всю ось действительных чисел, т.е. ![]() , окончательно получим
, окончательно получим
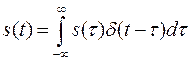 . (1.19)
. (1.19)
Итак, если сигнал ![]() умножить на
умножить на ![]() - функцию и произведение проинтегрировать по времени, то результат будет равен значению сигнала в точке, где сосредоточен дельта-импульс. Выражение (1.19) как раз и отображает фильтрующее свойство
- функцию и произведение проинтегрировать по времени, то результат будет равен значению сигнала в точке, где сосредоточен дельта-импульс. Выражение (1.19) как раз и отображает фильтрующее свойство ![]() - функции.
- функции.
1.4. Геометрическое представление сигналов
В современной теории радиотехнических сигналов широкое применение находят геометрические представления сигналов, использующие такие понятия как пространство, вектор, расстояние, проекция и т.д. Поэтому, для уяснения сущности геометрического представления необходимо познакомиться с этими понятиями.
Как уже подчеркивалось выше, для передачи сообщений в РТИС используется множество сигналов ![]() , образующее ансамбль сигналов. Это множество может быть непрерывным (континуальным), либо дискретным (счетным). В свою очередь дискретные множества могут быть конечными, либо бесконечными. При геометрическом представлении говорят, что множество
, образующее ансамбль сигналов. Это множество может быть непрерывным (континуальным), либо дискретным (счетным). В свою очередь дискретные множества могут быть конечными, либо бесконечными. При геометрическом представлении говорят, что множество ![]() образует пространство сигналов.
образует пространство сигналов.
Любое пространство предполагает наличие системы координат. Пространство, в котором обитает человек, характеризуется декартовой системой координат, характеризующейся наличием трех взаимно перпендикулярных координатных осей. Тогда с любой точкой пространства будут связаны три вещественных числа, которые можно рассматривать как координаты точки в пространстве.
Рассмотрим как можно распространить указанные понятия на радиотехнические сигналы. В качестве примера приведем представление произвольного сигнала ![]() длительностью
длительностью ![]() в виде суммы двух неперекрывающихся прямоугольных импульсов с высотой соответственно
в виде суммы двух неперекрывающихся прямоугольных импульсов с высотой соответственно ![]() и
и ![]() и длительностью
и длительностью ![]() (рис 1.8).
(рис 1.8).
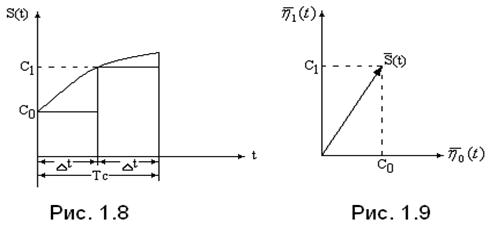
Т.к. импульсы не перекрываются во времени (проекция одного импульса на другой по оси времени равна нулю), то совокупность двух импульсов, отображающих сигнал ![]() , можно представить точкой в двумерной системе координат, образованной взаимноперпендикулярными векторами
, можно представить точкой в двумерной системе координат, образованной взаимноперпендикулярными векторами ![]() и
и ![]() (рис.1.9). Отрезок прямой, проведенный из начала системы координат в точку с координатами
(рис.1.9). Отрезок прямой, проведенный из начала системы координат в точку с координатами ![]() и
и ![]() представляет собой вектор
представляет собой вектор ![]() сигнала
сигнала ![]() при его данном динамическом представлении. Тогда математически его можно записать в виде
при его данном динамическом представлении. Тогда математически его можно записать в виде
![]() .
.
Если представить ![]() тремя импульсами, то сигнал
тремя импульсами, то сигнал ![]() будет отображаться вектором
будет отображаться вектором ![]() в трехмерном пространстве, четырьмя импульсами-вектором в четырехмерном пространстве, n импульсами-вектором в n-мерном пространстве. Таким образом, в общем случае сигнал
в трехмерном пространстве, четырьмя импульсами-вектором в четырехмерном пространстве, n импульсами-вектором в n-мерном пространстве. Таким образом, в общем случае сигнал ![]() отображается вектором
отображается вектором ![]() в абстрактном n-мерном пространстве. При этом пространство может быть бесконечномерным.
в абстрактном n-мерном пространстве. При этом пространство может быть бесконечномерным.
Отметим, что совокупность векторов ![]() образуют координатный базис пространства. Очевидно, с изменением значений сигнала
образуют координатный базис пространства. Очевидно, с изменением значений сигнала ![]() во времени длина вектора
во времени длина вектора ![]() и его положение в пространстве будет также меняться.
и его положение в пространстве будет также меняться.
Для дальнейшего рассмотрения геометрического представления зафиксируем момент времени ![]() , т.е. сделаем как бы фотографический снимок пространства. Это позволит на время абстрагироваться от динамики изменения сигнала и рассмотреть свойства пространства, используемого для геометрического представления. Кроме того, при характеристике пространства будем использовать его n-мерную модель, а для графических иллюстраций - двумерное пространство.
, т.е. сделаем как бы фотографический снимок пространства. Это позволит на время абстрагироваться от динамики изменения сигнала и рассмотреть свойства пространства, используемого для геометрического представления. Кроме того, при характеристике пространства будем использовать его n-мерную модель, а для графических иллюстраций - двумерное пространство.
Исходя из этих предположений, вектор сигнала ![]() можно записать следующим образом
можно записать следующим образом
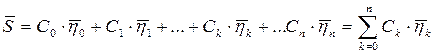 . (1.20)
. (1.20)
В теории радиотехнических сигналов пространство для геометрического представления должно быть линейным.
Линейное пространство обладает следующими основными свойствами:
- если векторы ![]() и
и ![]() принадлежат пространству
принадлежат пространству ![]() , то и вектор
, то и вектор ![]() также принадлежит этому пространству, причем (рис.1.10)
также принадлежит этому пространству, причем (рис.1.10)
![]() ; (1.21)
; (1.21)
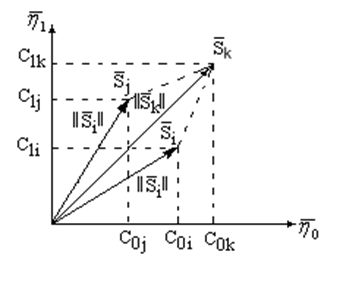
Рис. 1.10
- определена операция умножения вектора ![]() на любое вещественное число
на любое вещественное число ![]() , причем
, причем
![]() ; (1.22)
; (1.22)
- пространство содержит нулевой элемент ![]() , причем
, причем
![]() . (1.23)
. (1.23)
Поскольку при анализе сигналов, как правило, пользуются количественными характеристиками, пространство геометрического представления должно позволять определять длину векторов для их сравнения. Длину вектора называют нормой ![]() , а пространство, в котором определена норма - нормированным пространством. Основными свойствами линейного нормированного пространства являются:
, а пространство, в котором определена норма - нормированным пространством. Основными свойствами линейного нормированного пространства являются:
- для любого вещественного числа ![]() норма
норма
![]() ; (1.24)
; (1.24)
- если ![]() и
и ![]() - два вектора, принадлежащие линейному нормированному пространству, то:
- два вектора, принадлежащие линейному нормированному пространству, то:
![]() . (1.25)
. (1.25)
Свойство (1.25) отображает так называемое правило треугольника, известное из курса геометрии, в справедливости которого можно убедиться из рис.1.10.
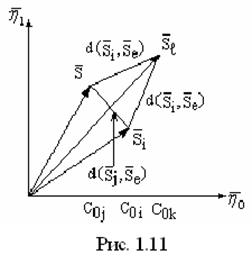
В качестве нормы в теории радиотехнических сигналов используют величину
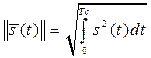 . (1.26)
. (1.26)
Очевидно квадрат нормы
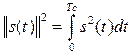 , представляет собой энергию сигнала.
, представляет собой энергию сигнала.
Введение понятия нормы позволяет определять длину векторов, представляющих сигналы в линейном нормированном пространстве, но не позволяет определять расстояние между векторами. Для того чтобы это стало возможным необходимо ввести понятие расстояния между векторами ![]() и
и ![]() , т.е. величину
, т.е. величину ![]() , называемую метрикой. Тогда линейное нормированное пространство становится метрическим.
, называемую метрикой. Тогда линейное нормированное пространство становится метрическим.
Метрика пространства должна удовлетворять условиям:
- расстояние между одинаковыми векторами равно нулю, т.е.
![]() ; (1.27)
; (1.27)
- расстояние между векторами
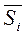 и
и 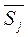 , должно быть равно расстоянию между
, должно быть равно расстоянию между 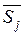 и
и 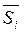 , т.е.
, т.е.
![]() (1.28)
(1.28)
- должно выполняться правило треугольника, т.е.
![]() . (1.29)
. (1.29)
В теории радиотехнических сигналов в качестве метрики используют норму разности двух сигналов
![]() . (1.30)
. (1.30)
Нетрудно убедиться, что величина (1.30) удовлетворяет всем аксиомам метрического пространства.
И, наконец, взаимное расположение двух векторов пространстве оценивается величиной угла ![]() между ними, который определяется выражением
между ними, который определяется выражением
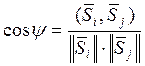 , (1.31)
, (1.31)
где числитель представляет собой скалярное произведение векторов.
Таким образом, для геометрического представления сигналов в радиотехнике используется линейное метрическое нормированное пространство. Если пространство конечномерное (координатный базис содержит конечное число векторов ![]() ), то такое пространство называют Евклидовым. Бесконечномерное пространство называется Гильбертовым пространством.
), то такое пространство называют Евклидовым. Бесконечномерное пространство называется Гильбертовым пространством.
1.5. Обобщенное спектральное представление сигналов
При рассмотрении геометрического представления сигналов мы зафиксировали пространство в какой-то момент времени ![]() . Снимем это ограничение и будем полагать, что каждый вектор
. Снимем это ограничение и будем полагать, что каждый вектор ![]() координатного базиса представляет собой функцию времени
координатного базиса представляет собой функцию времени ![]() . Переходя к функциям времени выражение (1.31) можно переписать следующим образом применительно для функций координатного базиса
. Переходя к функциям времени выражение (1.31) можно переписать следующим образом применительно для функций координатного базиса ![]() и
и ![]()
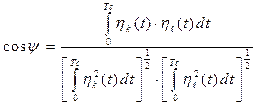 , (1.32)
, (1.32)
Но вектора ![]() и
и ![]() взаимноперпендикулярны, т.е. угол между ними составляет
взаимноперпендикулярны, т.е. угол между ними составляет ![]() =900, а
=900, а ![]() .
.
Приравнивая (1.32) к нулю и учитывая, что нормы ![]() и
и ![]() всегда отличны от нуля, получим:
всегда отличны от нуля, получим:
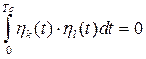 . (1.33)
. (1.33)
Две функции ![]() и
и ![]() , скалярное произведение (1.33) которых равно нулю, называют ортогональными функциями. Таким образом, декартова система координат при геометрическом представлении соответствует системе ортогональных функций
, скалярное произведение (1.33) которых равно нулю, называют ортогональными функциями. Таким образом, декартова система координат при геометрическом представлении соответствует системе ортогональных функций ![]() . Поскольку по определению
. Поскольку по определению
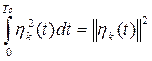 ,
,
то система функций ![]() является ортогональной, если выполняется условие
является ортогональной, если выполняется условие
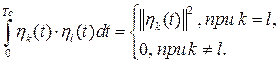 (1.34)
(1.34)
При выполнении условия
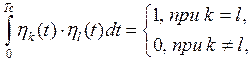 (1.35)
(1.35)
система функций называется ортонормированной. Нетрудно убедиться, что нормировка осуществляется делением каждой функции ![]() на ее норму. С геометрической точки зрения каждая функция ортонормированной системы соответствует единичному вектору – орту.
на ее норму. С геометрической точки зрения каждая функция ортонормированной системы соответствует единичному вектору – орту.
С учетом вышеизложенного при условии конечной энергии сигнала на интервале (0,Тс), т.е.
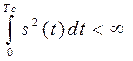 ,
,
выражение (1.20) можно записать следующим образом
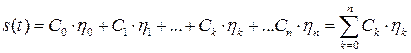 . (1.36)
. (1.36)
Выражение (1.36) представляет собой разложение сигнала ![]() на составляющие в системе ортогональных базисных функций (в ортогональном базисе) и называется обобщенным рядом Фурье.
на составляющие в системе ортогональных базисных функций (в ортогональном базисе) и называется обобщенным рядом Фурье.
Если число ортогональных функций в базисе ![]() бесконечно, то обобщенный ряд Фурье описывается следующим выражением
бесконечно, то обобщенный ряд Фурье описывается следующим выражением
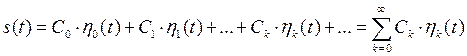 . (1.37)
. (1.37)
В дальнейшем мы будем пользоваться именно таким представлением обобщенного ряда Фурье.
Для определения значений ![]() умножим обе части (1.37) на
умножим обе части (1.37) на ![]() и проинтегрируем произведение в пределах
и проинтегрируем произведение в пределах ![]()
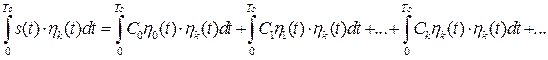 (1.38)
(1.38)
В силу ортогональности функций ![]() все слагаемые в (1.38) будут равны нулю кроме слагаемого, в котором индексы функций совпадают. Тогда выражение (1.38) примет следующий вид
все слагаемые в (1.38) будут равны нулю кроме слагаемого, в котором индексы функций совпадают. Тогда выражение (1.38) примет следующий вид
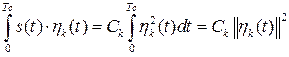 .
.
Отсюда следует, что
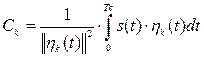 . (1.39)
. (1.39)
Отдельная функция ![]() называется спектральной составляющей сигнала, а совокупность коэффициентов
называется спектральной составляющей сигнала, а совокупность коэффициентов ![]() носит название спектра сигнала в данной системе базисных функций. Спектр сигнала полностью определяет его свойства.
носит название спектра сигнала в данной системе базисных функций. Спектр сигнала полностью определяет его свойства.
И, в заключение, выясним, как связаны между собой энергия сигнала в целом и его спектральных составляющих. Для простоты сначала положим, что сигнал ![]() представлен всего двумя спектральными составляющими
представлен всего двумя спектральными составляющими
![]() . (1.40)
. (1.40)
Так как энергия сигнала
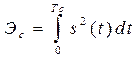 , (1.41)
, (1.41)
то, подставляя (1.40) в (1.41), получим
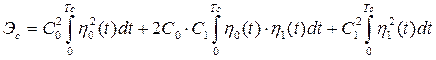 .
.
В силу ортогональности ![]() и
и ![]() второе слагаемое будет равно нулю. Тогда энергию сигнала можно представить формулами
второе слагаемое будет равно нулю. Тогда энергию сигнала можно представить формулами
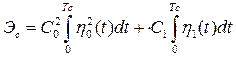
или
![]() .
.
Распространяя полученный результат на систему ортогональных функций ![]() , получим
, получим
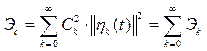 , (1.42)
, (1.42)
Где ![]() – энергия k-той составляющей.
– энергия k-той составляющей.
Если ![]() - система ортонормированных функций, то (1.42) принимает вид:
- система ортонормированных функций, то (1.42) принимает вид:
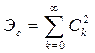 . (1.43)
. (1.43)
Выражения (1.42) или (1.43) представляют собой равенство Парсеваля, которое означает, что энергия сигнала ![]() равна сумме энергий всех спектральных составляющих. То же самое справедливо и для средней мощности сигнала.
равна сумме энергий всех спектральных составляющих. То же самое справедливо и для средней мощности сигнала.
Итак, выражения (1.36) и (1.37) не конкретизируют вид функций ![]() . В качестве таких функций в радиотехнике рассматриваются тригонометрические функции, функции Уолша, Хаара и ряд других. Поэтому перейдем к рассмотрению спектрального анализа сигналов в конкретных базисных системах.
. В качестве таких функций в радиотехнике рассматриваются тригонометрические функции, функции Уолша, Хаара и ряд других. Поэтому перейдем к рассмотрению спектрального анализа сигналов в конкретных базисных системах.

