4.2.1. Векторное представление синусоиды
4.2.4. Амплитудная манипуляция
Полосовая модуляция (аналоговая или цифровая) — это процесс преобразования информационного сигнала в синусоидальную волну; при цифровой модуляции синусоида на интервале Т называется цифровым символом. Синусоиды могут отличаться по амплитуде, частоте и фазе. Таким образом, полосовую модуляцию можно определить как процесс варьирования амплитуды, частоты или фазы (или их комбинаций) радиочастотной несущей согласно передаваемой информации. В общем виде несущая записывается следующим образом.
(4.1)
Здесь A(t) — переменная во времени амплитуда, а 
— переменный во времени угол. Угол удобно записывать в виде
(4.2)
так что
(4.3)
где ω — угловая частота несущей, а 
— ее фаза. Частота может записываться как переменная f или как переменная ω. В первом случае частота измеряется в герцах (Гц), во втором — в радианах в секунду (рад/с). Эти параметры связаны следующим соотношением 
.
Основные типы полосовой модуляции/демодуляции перечислены на рис. 4.1. Если для обнаружения сигналов приемник использует информацию о фазе несущей, процесс называется когерентным обнаружением (coherent detection); если подобная информация не используется, процесс именуется некогерентным обнаружением (no coherent detection). Вообще, в цифровой связи термины "демодуляция" (demodulation) и "обнаружение" (detection) часто используются как синонимы, хотя демодуляция делает акцент на восстановлении сигнала, а обнаружение — на принятии решения относительно символьного значения принятого сигнала. При идеальном когерентном обнаружении приемник содержит прототипы каждого возможного сигнала. Эти сигналы-прототипы дублируют алфавит переданных сигналов по всем параметрам, даже по радиочастотной фазе. В этом случае говорят, что приемник автоматически подстраивается под фазу входящего сигнала. В процессе демодуляции приемник перемножает и интегрирует входящий сигнал с каждым прототипом (определяет корреляцию). На рис. 4.1 под общим заголовком когерентной модуляции/демодуляции перечислены: фазовая манипуляция (phase shift keying — PSK), частотная манипуляция (frequency shift keying — FSK), амплитудная манипуляция (amplitude shift keying — ASK), модуляция без разрыва фазы (continuous phase modulation — CPM) и смешанные комбинации этих модуляций. Основные форматы полосовой модуляции рассмотрены в данной главе. Некоторые специализированные форматы, такие как квадратурная фазовая манипуляция, со сдвигом (onset quadrature PSK — OQPSK), манипуляция с минимальным сдвигом (minimum shift keying — MSK), принадлежащие к классу модуляций СРМ, и квадратурная амплитудная модуляция (quadrature amplitude modulation — QAM), рассмотрены в главе 9.
Некогерентная демодуляция относится к системам, использующим демодуляторы, спроектированные для работы без знания абсолютной величины фазы входящего сигнала; следовательно, определение фазы в этом случае не требуется. Таким образом, преимуществом некогерентных систем перед когерентными является простота, а недостатком — большая вероятность ошибки (РЕ). На рис. 4.1 под заголовком некогерентной передачи сигналов перечислены модуляции, подобные используемым при когерентной передаче: DPSK, FSK, ASK, CPM и смешанные их комбинации. Подразумевается, что для некогерентного приема информация о фазе не используется; так почему же под заголовком "некогерентная передача" указана одна из форм фазовой манипуляции? Это вызвано тем, что одну из важных форм PSK можно отнести к некогерентной (или дифференциально когерентной), поскольку она не требует согласования по фазе с принятой несущей. При использовании этой "псевдо-PSK", называемой дифференциальной фазовой манипуляцией (differential PSK — DPSK), в процессе обнаружения текущего символа в качестве опорной фазы применяется фаза предыдущего символа. Подробно этот вопрос рассмотрен в разделах 4.5.1 и 4.5.2.
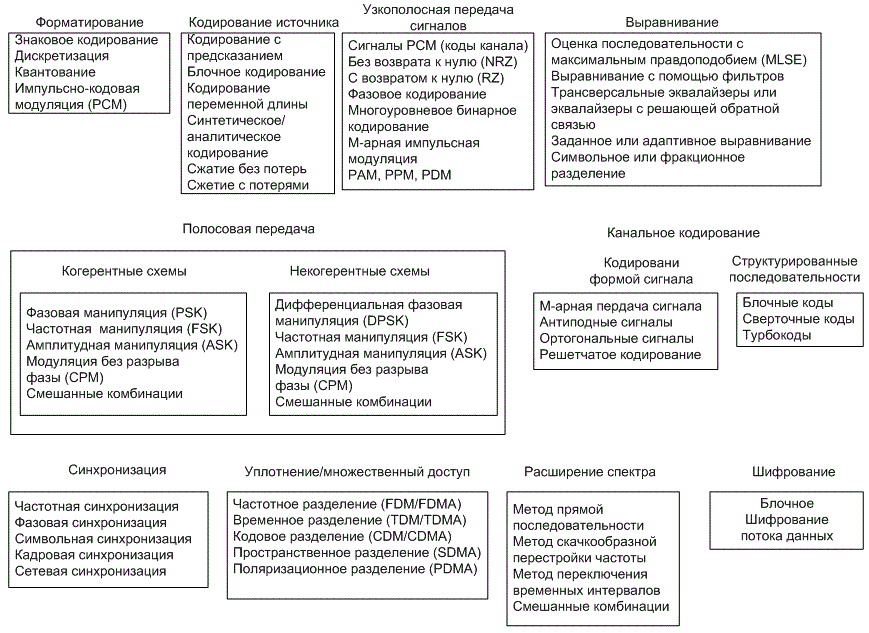
Рис 4.1. Основные преобразования цифровой связи
4.2.1. Векторное представление синусоиды
Используя известное тригонометрическое равенство, называемое теоремой Эйлера, введем комплексную запись синусоидальной несущей.
(4.4)
Возможно, кто-то чувствует себя уютнее при использовании более простой, привычной записи 
или 
. Возникает естественный вопрос: что нам дает комплексная запись? Далее будет показано (раздел 4.6), что такая форма записи облегчает описание реализации реальных модуляторов и демодуляторов. Здесь же мы рассмотрим общие преимущества представления несущей в комплексной форме, приведенной в формуле (4.4).
Во-первых, при комплексной записи в компактной форме, 
, указаны два важных компонента любой синусоидальной несущей волны, называемые взаимно ортогональными синфазной (действительной) и квадратурной (мнимой) составляющими. Во-вторых, как показано на рис. 4.2, немодулированная несущая удобно представляется в полярной системе координат в виде единичного вектора с постоянной скоростью ω0 рад/с, вращающегося против часовой стрелки. При увеличении t (от t0 до t1) мы можем изобразить переменные во времени проекции вращающегося вектора на синфазной (l) и квадратурной (Q) осях. Эти декартовы оси обычно называются синфазным (l channel) и квадратурным каналом (Q channel), а их проекции представляют взаимно ортогональные составляющие
Рис 4.2. Векторное представление синусоиды
cигнала, связанные с этими каналами. В-третьих, процесс модуляции несущей можно рассматривать как систематическое возмущение вращающегося вектора (и его проекций).
Рассмотрим, например, несущую, амплитудно-модулированную синусоидой с единичной амплитудой и частотой ωm, где ωm<<ω0. Переданный сигнал имеет следующий вид.
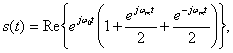(4.5)
где Re{x} — действительная часть комплексной величины {x}. На рис. 4.3 показано, что вращающийся вектор , представленный на рис. 4.2, возмущается двумя боковыми членами — 
, вращающимся против часовой стрелки, и 
, вращающимся по часовой стрелке. Боковые векторы вращаются намного медленнее, чем вектор несущей волны. В результате модулированный вращающийся вектор несущей волны растет и уменьшается согласно указаниям боковых полос, но частота его вращения остается постоянной; отсюда и название "амплитудная модуляция".
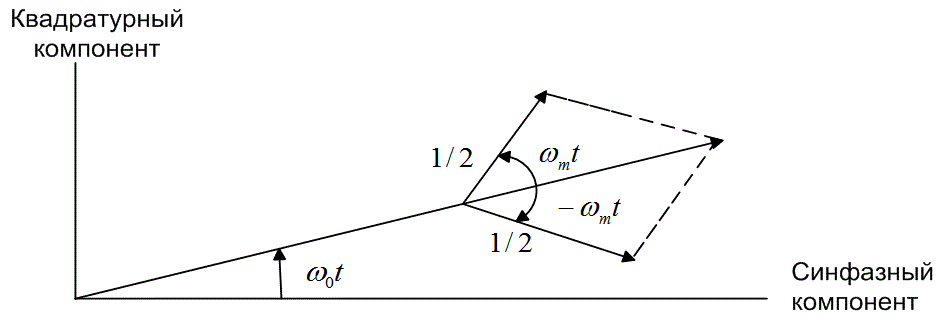
Рис 4.3. Амплитудная модуляция
Еще один пример, иллюстрирующий полезность векторного представления, — это частотная модуляция (frequency modulation — FM) несущей похожей синусоидой с частотой вращения ωm рад/с. Аналитическое представление узкополосной частотной модуляции (narrowband FM — NFM) подобно представлению амплитудной модуляции и описывается выражением:
(4.6)
где β — коэффициент модуляции [1]. На рис. 4.4 показано, что, как и в предыдущем случае, вектор несущей волны возмущается двумя боковыми векторами. Но поскольку один из них, как указано в формуле (4.6), имеет знак "минус", симметрия боковых векторов, вращающихся по часовой стрелке и против нее, отличается от имеющейся в случае амплитудной модуляции. При модуляции AM симметрия приводит к увеличению и уменьшению вектора несущей волны со временем. В случае модуляции NFM симметрия боковых векторов (на 90° отличающаяся от симметрии AM) приводит к ускорению и замедлению вращения вектора согласно указаниям боковых полос, при этом амплитуда остается неизменной; отсюда название "частотная модуляция".
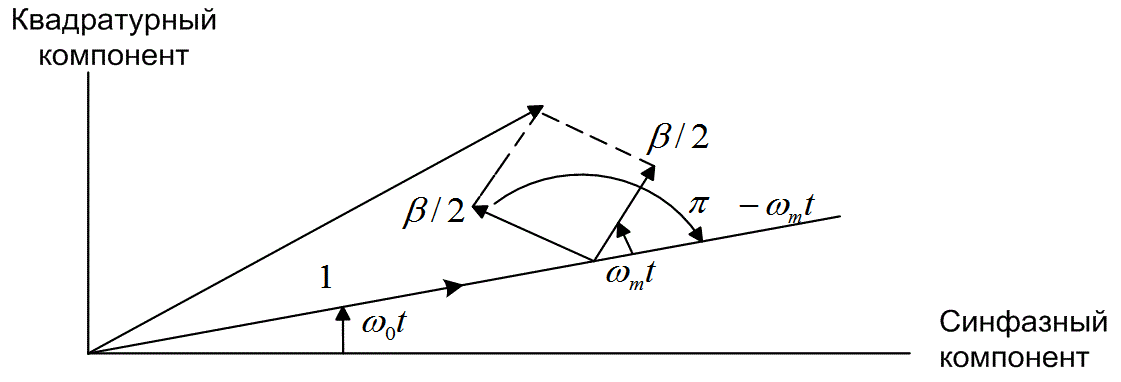
Рис 4.4. Узкополосная частотная модуляция
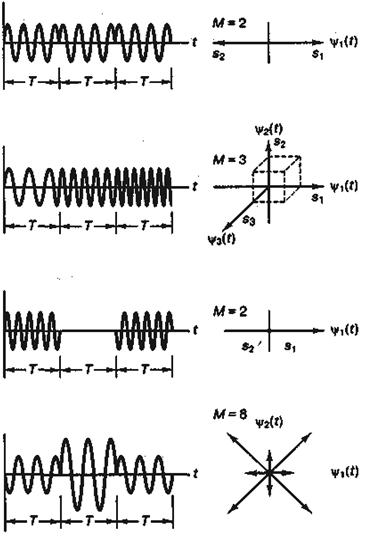
На рис. 4.5 изображены наиболее распространенные форматы цифровой модуляции: PSK, FSK, ASK и смешанная комбинация ASK и PSK (обозначаемая как ASK/PSK, или АРК). В первом столбце указаны аналитические выражения, во втором — временная диаграмма, а в третьем — векторная диаграмма. В общем случае M-арной передачи сигналов устройство обработки получает k исходных битов (или канальных битов, если используется кодирование) в каждый момент времени и указывает модулятору произвести один из М = 2k возможных сигналов. Частным случаем M-уровневой модуляции является бинарная с k=1.
На рис. 4.2 несущая волна представлялась как вектор, вращающийся на плоскости со скоростью, равной частоте несущей, ω0 рад/с. На рис. 4.5 векторная схема каждой цифровой модуляций представляет совокупность информационных сигналов (векторов или точек пространства сигналов) без указания времени. Другими словами, на рис. 4.5 не отображено вращение немодулированного сигнала с постоянной скоростью, а представлено только взаимное расположение векторов-носителей информации. Стоит обратить внимание, что в примерах на рис. 4.5 значения размера множества M отличаются.
Аналитическое представление Сигнал Вектор
а) PSK 
б) FSK 
в) ASK 
г) ASK/PSK (APK) 
Рис. 4.5. Виды цифровых модуляций: a) PSK; б) FSK; в) ASK; г) ASK/PSK (АРК)
4.2.2. Фазовая манипуляция
Фазовая манипуляция (phase shift keying — PSK) была разработана в начале развития программы исследования дальнего космоса; сейчас схема PSK широко используется в коммерческих и военных системах связи. Сигнал в модуляции PSK имеет следующий вид.
(4.7)
Здесь фазовый член 
может принимать M дискретных значений, обычно определяемых следующим образом.
На рис. 4.5, а приведен пример двоичной (M = 2) фазовой манипуляции (binary PSK — BPSK). Параметр Е — это энергия символа, Т — время передачи символа, . Работа схемы модуляции заключается в смещении фазы модулируемого сигнала s,(r) на одно из двух значений, нуль или π (180°). Типичный вид сигнала в модуляции BPSK приведен на рис. 4.5, а, где явно видны характерные резкие изменения фазы при переходе между символами; если модулируемый поток данных состоит из чередующихся нулей и единиц, такие резкие изменения будут происходить при каждом переходе. Модулированный сигнал можно представить как вектор на графике в полярной системе координат; длина вектора соответствует амплитуде сигнала, а его ориентация в общем M-арном случае — фазе сигнала относительно других М - 1 сигналов набора. При модуляции BPSK векторное представление дает два противофазных (180°) вектора. Наборы сигналов, которые могут быть представлены подобными противофазными векторами, называются антиподными.
4.2.3. Частотная манипуляция
Общее аналитическое выражение для сигнала в частотной манипуляции (frequency shift keying — FSK) имеет следующий вид.
(4.8)
Здесь частота ω0 может принимать М дискретных значений, а фаза φ является произвольной константой. Схематическое изображение сигнала в модуляции FSK дано на рис. 4.5, б, где можно наблюдать типичное изменение частоты (тона) в моменты переходов между символами. Такое поведение характерно только для частного случая FSK, называемого частотной манипуляцией без разрыва фазы (continuous-phase FSK — CPFSK); она описана в разделе 9.8. В общем случае многочастотной манипуляции (multiple frequency shift keying — MFSK) переход к другому тону может быть довольно резким, поскольку непрерывность фазы здесь не обязательна. В приведенном примере М = 3, что соответствует такому же числу типов сигналов (троичной передаче); отметим, что значение М = 3 было выбрано исключительно для демонстрации на рисунке взаимно перпендикулярных осей. На практике М обычно является ненулевой степенью двойки (2, 4, 8, 16, ...), что довольно сложно изобразить графически. Множество сигналов описывается в декартовой системе координат, где каждая координатная ось представляет синусоиду определенной частоты. Как говорилось ранее, множества сигналов, которые описываются подобными взаимно перпендикулярными векторами, называются ортогональными (orthogonal). Не все схемы FSK относятся к ортогональным. Чтобы множество сигналов было ортогональным, оно должно удовлетворять критерию, выраженному в формуле (3.69). Этот критерий навязывает определенные условия на взаимное размещение тонов множества. Расстояние по частоте между тонами, необходимое для удовлетворения требования ортогональности.
4.2.4. Амплитудная манипуляция
Сигнал в амплитудной манипуляции (amplitude shift keying — ASK), изображенной на рис. 4.5, в, описывается выражением 
(4.9)
где амплитудный член 
может принимать М дискретных значений, а фазовый член φ — это произвольная константа. На рис. 4.5, в М выбрано равным 2, что соответствует двум типам сигналов. Изображенный на рисунке сигнал в модуляции ASK может соответствовать радиопередаче с использованием двух сигналов, амплитуды которых равны 0 и 
. В векторном представлении использованы те же фазово-амплитудные полярные координаты, что и в примере для модуляции PSK. Правда, в данном случае мы видим один вектор, соответствующий максимальной амплитуде с точкой в начале координат, и второй, соответствующий нулевой амплитуде. Передача сигналов в двухуровневой модуляции ASK — это одна из первых форм цифровой модуляции, изобретенных в начале столетия для беспроводной телеграфии. В настоящее время простая схема ASK в системах цифровой связи уже не используется.
4.2.5. Амплитудно-фазовая манипуляция
Амплитудно-фазовая манипуляция (amplitude phase keying — АРК) — это комбинация схем ASK и PSK. Сигнал в модуляции АРК изображен на рис. 4.5, г и выражается как
(4.10)
с индексированием амплитудного и фазового членов. На рис. 4.5, г можно видеть характерные одновременные (в моменты перехода между символами) изменения фазы и амплитуды сигнала в модуляции АРК. В приведенном примере М=8, что соответствует 8 сигналам (восьмеричной передаче). Возможный набор из восьми векторов сигналов изображен на графике в координатах "фаза-амплитуда". Четыре показанных вектора имеют одну амплитуду, еще четыре — другую. Векторы ориентированы так, что угол между двумя ближайшими векторами составляет 45°. Если в двухмерном пространстве сигналов между М сигналами набора угол прямой, схема называется квадратурной амплитудной модуляцией (quadrature amplitude modulation — QAM); примеры QAM рассмотрены в главе 9.
Векторные представления модуляций, изображенные на рис. 4.5 (за исключением случая FSK), изображены графиками, полярные координаты которых представляют амплитуду и фазу сигнала. Схема FSK подразумевает ортогональную передачу (см. раздел 4.5.4) и описывается в декартовой системе координат, где каждая ось представляет тон частоты (
), совокупность которых формирует М-значный набор ортогональных тонов.
4.2.6. Амплитуда сигнала
Амплитуды сигналов, представленные в формулах (4.7)-(4.10), имеют одинаковый вид для всех форматов модуляции. Выведем это. Сигнал описывается формулой
(4.11)
где А — максимальная амплитуда сигнала. Поскольку максимальное значение в V2 раза больше его среднеквадратического (root-mean-square — rms) значения, можем записать следующее.
Предполагается, что сигнал выражен через колебания тока или напряжения, так что 
представляет среднюю мощность Р (нормированную на 1 Ом). Значит, можем записать следующее.
(4.12)
Заменяя Р (единицы измерения — ватт) на Е (джоули)/Т (секунды), получаем следующее.
(4.13)
Итак, амплитуду сигнала можно записать либо в общем виде, как в формуле (4.11), либо через , как в формуле (4.13). Поскольку ключевой параметр при определении вероятности ошибки в процессе обнаружения — это энергия принятого сигнала, зачастую удобнее использовать запись в форме (4.13), так как в этом случае вероятность ошибки ре можно получить сразу как функцию энергии сигнала.