С относительно медленного устройства ввода (имеющего два порта: порт данных №12 и порт состояний №8) ввести 64 однобайтовых числа со знаком, представленных в дополнительном коде. Вычислить среднее арифметическое чисел и поместить его в прямом коде в ячейку 05АВ оперативной памяти. Готовность устройства ввода определяется значением 1 в младшем разряде числа, выдаваемого из порта №8. для исключения потери точности перед сложением чисел и следует представить в двухбайтовом формате.

Требуется составить алгоритм и реализовать его.

Алгоритм представлен на рис. 1.

Комментарии к алгоритму:

Блок 1: В пару регистров HL записывается начальный адрес массива для записи 64 чисел.
Блок 2: Организация счетчика циклов (64 цикла в 16-ричной системе счисления).
Блок 3: Ввод сигнала готовности через УВВ 8
Блоки 4-5: анализ сигнала готовности.
Блок 6: ввод очередного числа через УВВ 12
Блок 7: запись числа в оперативную память.
Блок 8: модификация адреса (берется следующий элемент массива из соседней ячейки).
Блоки 9-10: организация цикла.
Блок 11: обнуление пары регистров ВС (там будет накапливаться сумма элементов массива).
Блок 12: организация счетчика циклов.
Блок 13: адрес начала массива.
Блок 14: вывод первого числа
Блок 15: модификация адреса.
Блок 16: запись накапливаемой суммы младших байтов в аккумулятор.
Блоки 17-18: увеличение содержимого регистра В, если есть перенос Т_С.
Блоки 19-20: организация цикла.
Блок 21: запоминание младшего байта суммы.
Блок 22: организация счетчика циклов для деления на 64.
Блок 23: вызов старшего байта в аккумулятор.
Блок 24: сдвиг вправо аккумулятора.
Блок 25: запоминание старшего байта в регистр В.
Блок 26: вызов младшего байта в аккумулятор.
Блок 27: Сдвиг вправо с учетом Т_С.
Блок 28: запоминание младшего байта в регистр С.
Блоки 29-30: организация цикла.
Блок 31: Запоминание результата.
Блок 32: конец программы.

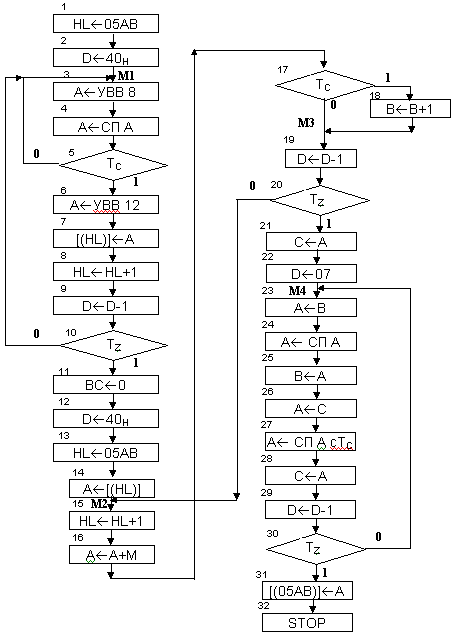
Рисунок 1. Алгоритм вычисления среднего арифметического 64 чисел.

В массиве из 15 чисел, хранящихся в ОЗУ начиная с адреса 0567₁₆, изменить порядок следования разрядов на обратный. После преобразования числа помещать на место исходных данных.

Составить алгоритм и программу, реализующие условие задачи.

Итак, нужно сделать следующее:

1. взять какое-то число из ОЗУ;
2. сдвинуть это число влево, при этом старший разряд попадет в признак Т_С.
3. взять значение промежуточного регистра и признак Т_С, полученный на предыдущем шаге, сдвинуть вправо.
4. (2) и (3) операции нужно повторить 8 раз подряд.
5. Организовать большой цикл, так как у нас 15 чисел для преобразования..

Для решения задачи воспользуемся следующими регистрами:

HL – пара регистров для обращения к ячейкам ОЗУ.
В – счетчик циклов для преобразования 15-ти чисел.
С - счетчик циклов для преобразования 1-го числа.
D и E – два промежуточных регистра.

Алгоритм приведен на рис.2.

Комментарии к алгоритму и программе:

Блок 1: Загрузка начального адреса массива.
Блок 2: Организация счетчика циклов (всего 15 чисел).
Блок 3: Организация счетчика циклов (всего 8 разрядов в каждом числе).
Блок 4: Обнуление промежуточных регистров.
Блок 5: Пересылка очередного числа в промежуточный регистр “D”.
Блок 6: Пересылка в аккумулятор.
Блок 7: Сдвиг влево аккумулятора.
Блок 8: Возврат в “D”.
Блок 9: Пересылка из “Е” в аккумулятор.
Блок 10: Сдвиг вправо аккумулятора.
Блок 11: Пересылка в регистр “Е”.
Блоки 12, 13: Организация малого цикла работы.
Блок 14: Пересылка преобразованного числа по старому адресу.
Блок 15: Модификация адреса.
Блоки 16, 17: Организация большого цикла работы.

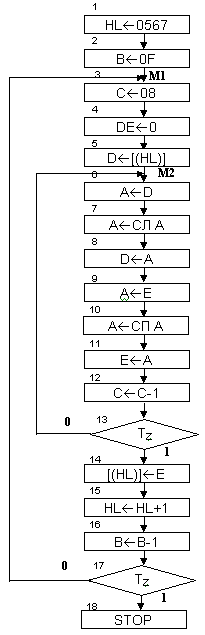
Рисунок 2. Алгоритм изменения порядка следования разрядов.

Массив из 19 5-ти – разрядных двоичных чисел без знака, выдаваемый устройством ввода (порт №10), преобразовать в десятичную систему счисления и полученные данные поместить в оперативную память, начиная с адреса 1АВС. Готовность устройства ввода задается сигналом из порта №11, содержащим 1 в старшем разряде.

Рассмотрим, как можно совершить преобразование двоичных чисел в десятичную систему с помощью сдвиговых регистров.

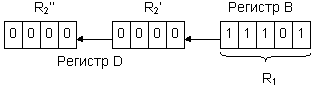
Пусть число, подлежащее преобразованию в десятичную систему счисления, хранится в регистре R₁ (рис.3.1). Результат преобразования (число в десятичной системе счисления) будем формировать в регистре R₂. разряды регистра R₂ делятся на 4-разрядные группы R₂’, R₂’’, R₂’’’ и т.д., каждая из которых предназначена для хранения одной десятичной цифры, представленной в двоичной системе счисления.

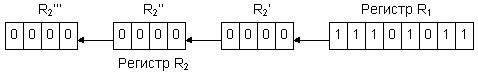
Рассматриваемый способ преобразования потребует выполнения последовательности операций сдвига влево содержимого регистров R₁ и R₂ с передачей выдвигаемого из регистра R₁ содержимого старшего разряда в освобождающийся младший разряд регистра R₂. двоичное число, выдвигаясь из регистра R₁, будет вдвигаться в регистр R₂. При этом необходимо учитывать следующую особенность выполнения сдвигов в регистре R₂. Единица, выдвигаемая при сдвиге из старшего разряда группы R₂’, имеет вес 2⁴=16. Однако поступая в группу R₂’’ (в разряд десятков), эта единица будет иметь вес 10. таким образом, при передаче единицы из R₂’ в R₂’’ происходит потеря 6 единиц. Для компенсации этой потери потребуется прибавить 6 единиц к содержимому R₂’. Можно показать, что выдвижение 1 из любой 4-разрядной группы регистра R₂ требует коррекции содержимого этой группы путем прибавления 6 единиц. Такая же коррекция требуется и в случае, когда после сдвига в 4-разрядной группе возникает число, большее или равное 10. В этом случае прибавление 6 единиц вызывает перенос из старшего разряда группы, который необходимо прибавлять к содержимому следующей 4-разрдной группы.

Более удобным оказывается способ, при котором коррекция производится не после сдвига, а до выполнения сдвига влево. В этом случае коррекция осуществляется прибавлением числа 3 (в результате сдвига оно удваивается и принимает значение 6), а признаком необходимости коррекции является наличие в 4-разрядной группе числа, большего или равного 5 (после сдвига это число оказывается большим или равным 10). При этом передача единицы в следующую 4-разрядную группу осуществляется только путем передачи переноса, возникающего в процессе сдвига (т.е. исключается необходимость прибавления единицы к содержимому группы, как в случае, когда коррекция выполняется после операции сдвига).

Если число разрядов регистра R₁ равно n, то преобразования завершается после n-кратного выполнения сдвига.

Мы имеем 19 чисел, каждое из которых 5-разрядное, а для преобразования одного 5-разрядного числа необходим один регистр:

Алгоритм преобразования одного числа представлен на рис.3.1

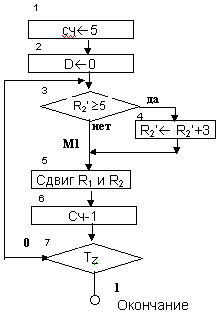
Рисунок 3.1. Алгоритм преобразования одного числа из двоичной системы счисления в десятичную.

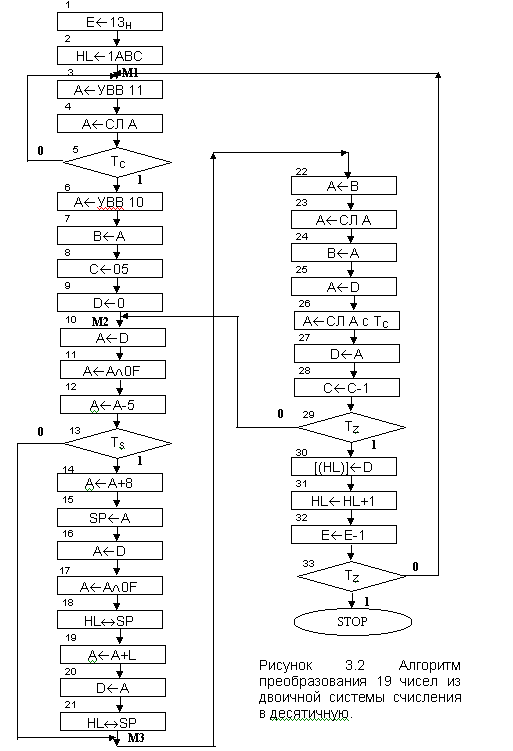
Полный алгоритм решения задачи представлен на рис. 3.2.

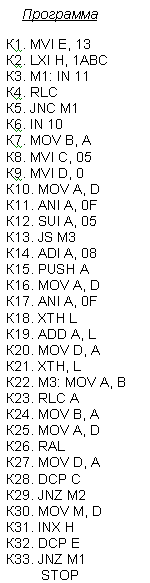
Комментарии к алгоритму и программе.

Блок 1: Организация счетчика циклов (19 чисел)
Блок 2: Начальный адрес массива.
Блоки 3-5: Синхронизация по сигналу ввода с устройства ввода №11.
Блок 6: ввод сигнала с устройства ввода №10.
Блок 7: Пересылка из аккумулятора в регистр "В".
Блок 8: Организация малого счетчика циклов.
Блок 9: Обнуление R₂.
Блок 10: Пересылка R₂ в аккумулятор.
Блок 11: Анализ R₂'.
Блоки 12, 13: Проверка условия R₂' ³ 5.
Блоки 14-21: Коррекция R₂'+3 и пересылка результата в регистр "D".
Блоки 22-27: Сдвиг R₁ и R₂/
Блоки 28, 29: Организация малого цикла преобразования двоичного числа в десятичное.
Блок 30: Пересылка результата преобразования.
Блок 31: Модификация адреса.
Блоки 32, 33: Организация большого цикла работы.
Блок 34: Останов.

Разделить два положительных однобайтовых числа, представленных в формате с фиксированной перед старшим разрядом запятой, находящихся по адресам 0789₁₆ и 078А₁₆. если частное больше или равно 1, то выдать сигнал переполнения в устройство вывода №3, в противном случае результат операции следует поместить в ячейку 078В₁₆ оперативной памяти.

Распределим регистры:

А – поместим делимое (адрес 0789);
В – поместим делитель (адрес 078А);
С – промежуточный регистр;
D – счетчик циклов;
Е – частное от деления.

Если будет переполнение регистра Е, то выведем на устройство вывода №3 сигнал 00_Н.

Алгоритм решения задачи представлен на рис.4

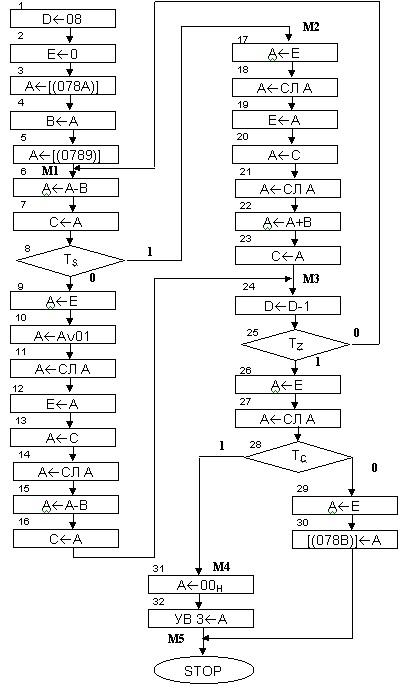
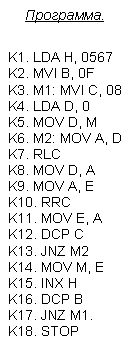
Рисунок 4. Алгоритм деления двух чисел.

Комментарии к программе:

К1 - организация цикла;
К2 - обнуление регистра, где будет храниться частное;
К3, К4 - пересылка делителя;
К5 - пересылка делимого;
К6, К7 - операция "С=А-В";
К8 - определение знака величины "С";
К9 - К12 - запись "1" в регистр Е и сдвиг на 1 разряд влево.
К13, К14 - операция сдвига влево регистра "С";
К15, К16 - операция "С=А-В";
К17 - К19 - запись "0" в регистр Е и сдвиг на 1 разряд влево.
К20, К21 - сдвиг влево в регистре "С";
К22, К23 - операция "С=А+В";
К24, К25 - организация цикла;
К26, К27, К28 - анализ частного (есть или нет переполнение регистра);
К29, К30 - запись частного от деления;
К31, К32 - вывод сигнала "переполнение";

Произвести умножение двухбайтового числа без знака на однобайтовое целое число без знака. Число хранится в оперативной памяти по адресам: множимое – 0А01, 0А02; множитель – 0А03. Результат умножения выдать на устройство вывода №1. Сигналом готовности устройства вывода является наличие единицы в данных, выдаваемых из порта №6.

Алгоритм решения задачи приведен на рис.5.

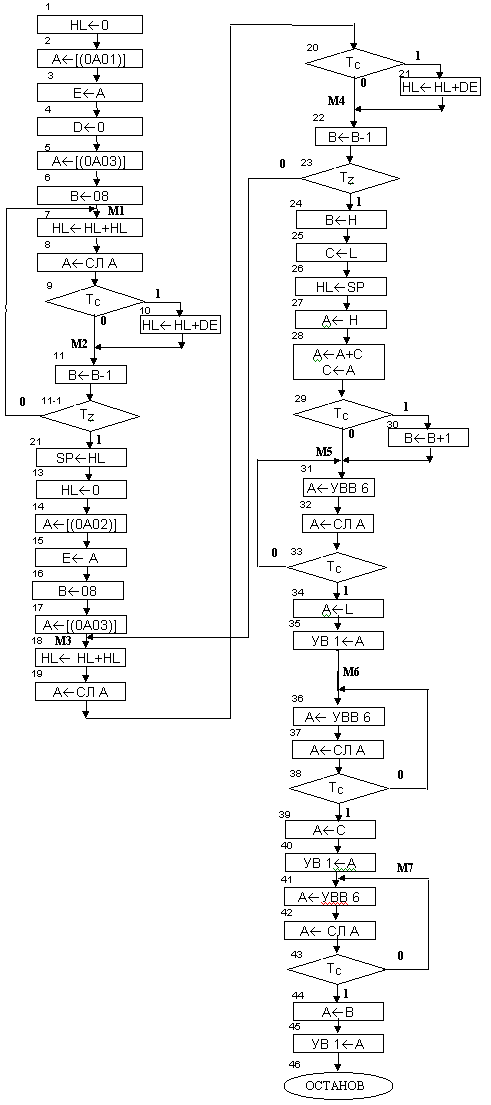
Рисунок 5.

Комментарии к программе

К1 – обнуление пары регистров HL для вычисления первого промежуточного произведения.
К2 – К4 – пересылка множимого (младший байт) в пару регистров DE.
К5 – пересылка множителя в аккумулятор.
К6 – счетчик циклов умножения.
К7 – сдвиг HL влево на 1 разряд.
К8 – сдвиг влево множителя.
К9 – анализ разряда множителя.
К10 – сложение пар регистров.
К11 – К11-1 – организация цикла работы.
К12 – запоминание в стеке результатов промежуточного умножения.
К13 – обнуление HL.
К14 – К15 – пересылка множимого (старшего байта) в пару регистров DE.
К16 – счетчик циклов.
К17 – пересылка множителя в аккумулятор.
К18 – сдвиг HL влево на 1 разряд.
К19 – К20 – сдвиг влево множителя и его анализ
К21 – сложение пары регистров.
К22 – К23 – организация цикла.
К24 – К25 – пересылка старшего байта в регистры ВС.
К26 – вывод младшего байта из стека.
К27 – пересылка старшего байта младшего промежуточного умножения.
К28 – сложение двух регистров и запоминание результата в регистре С.
К29, К30– перенос Т_С добавляется к старшему байту.
К31 – ввод сигнала с УВВ 6.
К32, К33 – анализ старшего разряда сигнала.
К34, К35 – вывод младшего байта результата на УВ 1.
К36 – ввод сигнала синхронизации.
К37 – К38 – анализ сигнала синхронизации.
К39, К40 – вывод среднего байта.
К41 – ввод сигнала синхронизации.
К42, К43 – анализ сигнала синхронизации.
К44, К45 – вывод старшего байта.
К46 – останов

В оперативной памяти хранятся два массива однобайтовых чисел со знаком, представленные в прямом коде. Каждый из массивов содержит 10 чисел. Начальные адреса массивов: 03АВ и 0А45. сформировать разность массивов в прямом коде и выдать ее на устройство ввода №12. Сигналом готовности устройства вывода является наличие единицы в старшем разряде данных, выдаваемых из порта №13.

Алгоритм решения задачи приведен на рис.6

Комментарии к алгоритму и программе

Блок 1: Организация счетчика циклов
Блок 2: Начальный адрес 1-го массива.
Блок 3: Начальный адрес 2-го массива.
Блок 4: Вывод очередного числа первого массива.
Блок 5: Разность двух чисел.
Блоки 6-8: Преобразование отрицательного числа в положительное (выдача необходима в прямом коде).
Блоки 9, 10: Промежуточное запоминание.
Блоки 11, 12: Модификация адреса.
Блоки 13-15: Синхронизация по УВВ 13: ввод числа, сдвиг влево для выявления старшего разряда и его анализ.
Блок 16: Пересылка из “Е” в аккумулятор.
Блок 17: Вывод числа.
Блоки 18, 19: Организация цикла.
Блок 20: Останов.

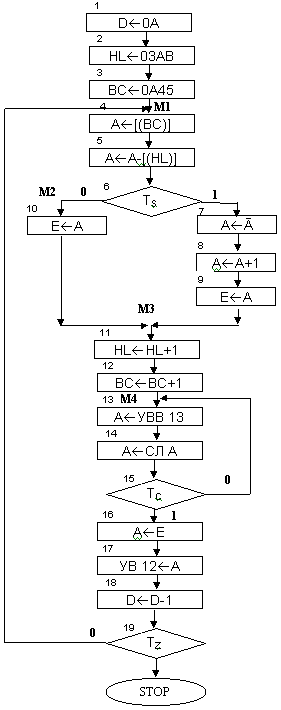
Рисунок 6. Алгоритм определения разности массивов.