Теория телетрафика – раздел теории массового обслуживания. Основы теории телетрафика заложил датский учёный А.К. Эрланг. Термин "трафик" соответствует термину "телефонная нагрузка". Последовательность сообщений (занятий) создает нагрузку на системы передачи и коммутации. Она определяется потоком вызовов и длительностью занятий канала.

Вызов – требование источника на установление соединения или передачу сообщения.

Поток вызовов – последовательность моментов поступления вызовов.

Длительность занятия – среднее время, в течение которого занят обслуживающий прибор при одном занятии.

В общем случае потоки вызовов являются случайными процессами. Точное математическое описание потоков невозможно, поэтому используются их модели.

Наиболее распространена модель в виде простейшего потока вызовов – это стационарный ординарный поток без последействия.

В большинстве случаев поток вызовов в ЧНН от группы источников численностью > 100 удовлетворительно описывается простейшим потоком.

В том случае, если число источников меньше 100, используют модель примитивного потока.

Примитивный поток – ординарный поток, параметр которого прямо пропорционален числу свободных источников.

Телефонная нагрузка – общая длительность занятия обслуживающих приборов в течение некоторого промежутка времени.

Единица измерения нагрузки 1 часо-занятие.

Интенсивность телефонной нагрузки – величина нагрузки в единицу времени, измеряется в Эрлангах

1 Эрл = 1 часо-занятие / час

Интенсивность телефонной нагрузки имеет сильные колебания, в том числе и в течение дня.

Час наибольшей нагрузки [ЧНН] – период суток, в течение которого нагрузка имеет наибольшее значение

Потери – часть поступающей нагрузки, которая не обслуживается из-за занятости обслуживающих приборов [16].

Различают виды коммутационных систем: коммутационные системы без потерь; коммутационные системы с потерями; коммутационные системы с ожиданием.

Дисциплиной обслуживания без потерь называется такая, при которой поступающий вызов немедленно обслуживается, и с потерями, если поступающий вызов либо получает отказ в обслуживании, либо обслуживание его задерживается на некоторое время.

По экономическим соображениям реальные коммутационные системы обычно проектируются с потерями. Различают следующие виды потерь: явные, условные и комбинированные.

Дисциплиной обслуживания с явными потерями называется такая, при которой поступающий на коммутационную систему вызов, получая отказ в обслуживании, покидает систему и в дальнейшем не оказывает на систему никакого влияния. При такой дисциплине обслуживания абонент, получив сигнал "занято", отказывается от дальнейших попыток установить соединение.

Дисциплиной обслуживания с условными потерями называется такая, при которой поступающий на коммутационную систему в момент отсутствия соединительных путей вызов не теряется, а обслуживается с ожиданием (дисциплина обслуживания с ожиданием). Если вызов обслуживается после многократных повторений попыток установить соединение, то имеет место дисциплина обслуживания с повторением.

Структура коммутационной системы характеризуется большим числом параметров: числом звеньев, числом, емкостью и способами связи коммутаторов и так далее. Наиболее удобной функцией распределения длительности обслуживания с точки зрения аналитического описания и анализа пропускной способности коммутационных систем является показательное распределение, так как оно не обладает последействием.

, (3.5)

где β =1/М(t) – параметр длительности обслуживания;

М(t) – математическое ожидание длительности обслуживания.

Одной из важнейших характеристик коммутационных систем является их эффективность. В качестве показателей эффективности наряду с экономическими (капитальными затратами, эксплуатационными расходами) широко используется и такой технический показатель, как пропускная способность.

Под способностью пропускной коммутационной системы понимается интенсивность обслуженной коммутационной системой нагрузки при заданном качестве обслуживания. Пропускная способность коммутационной системы зависит от величины потерь, емкости пучков линий, включенных в выходы коммутационной системы, от способа (схемы) объединения этих выходов, класса потока вызовов, структуры коммутационной системы. Распределения длительности обслуживания и дисциплины обслуживания.

Для количественной оценки качества обслуживания с явными потерями рассчитываются следующие величины: потери по вызовам – р_в; потери по времени - р_t., потери по нагрузке – ρн.

Потери по вызовам на отрезке времени [t₁, t₂) – это отношение числа потерянных за этот отрезок времени вызовов к числу поступивших за то же время вызовов.

Потери по нагрузке на отрезке времени [t₁, t₂) – это отношение потерянной за этот отрезок времени нагрузки к поступающей за то же время нагрузке.

Потери по времени за отрезок времени [t₁, t₂) – это доля времени, в течение которого все соединительные пути, доступные группе источников, заняты.

Если в выражения для потерь по вызовам, нагрузке и времени подставить математические ожидания соответствующих случайных величин, то можно говорить о вероятности потерь по вызовам, нагрузке и времени. Тогда формула для расчета р_в будет иметь вид:

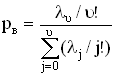, (3.6)

где λ – интенсивность потока вызовов; υ – количество каналов;

Формула 3.6 называется распределением Эрланга. Она показывает, что вероятность р_i зависит только от числа занятых линий i, емкости пучка υ и величины параметра потока вызовов λ. По этим соображениям вероятность р_i принято обозначать Е_i,υ(λ), ΰ вероятность р_υ – через Е_υ,υ(λ) θли Е_υ(λ).

Р_в = р_t = р_υ = Е_υ(λ).

При выводе формулы средняя длительность занятия принята равной единице; отсюда и параметр длительности занятий при показательном законе распределения β = 1. В общем случае при измерении длительности занятий в любых единицах времени (β 1) распределение Эрланга имеет следующий вид:

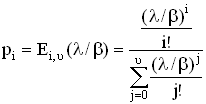, (3.7)

В частности, вероятность того, что в полнодоступном пучке заняты все υ линий (i = υ), πавна

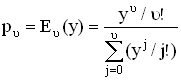, (3.8)

где y – интенсивность поступающей нагрузки

y = μ = μ/β = λ/β;

μ – интенсивность потока вызовов; – средняя длительность занятия.

Для простейшего потока, который является ординарным и стационарным, μ = λ. Тогда распределение Эрланга имеет вид:

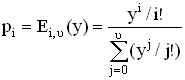, (3.9)

При 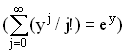распределение Эрланга преобразуется в распределение Пуассона:

, (3.10)

Для количественной оценки качество обслуживания с ожиданием рассчитываются характеристики: вероятность ожидания обслуживания для поступившего вызова – p(γ>0); βероятность ожидания для любого поступившего вызова свыше времени t, равна p(γ>t); среднее время ожидания по отношению ко всем поступившим вызовам – и по отношению только к задержанным вызовам – ; вероятность того, что длина очереди превышает заданную величину r, p(R>r); средняя длина очереди – . Основными характеристиками являются p(γ>0) и p(γ>t).

Для систем с ожиданием вероятность ожидания для поступившего вызова P(γ>0) – это отношение математических ожиданий числа задержанных в обслуживании за отрезок времени [t₁,t₂) вызовов к числу поступивших за рассматриваемый промежуток времени вызовов находится из выражения:

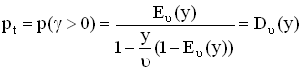, (3.11)

Выражение (3.6.6) называется второй формулой Эрланга. Формула табулирована. Таблицы позволяют по любым двум из трех параметров y, υ, p_t – определить третий.

Выражение (3.6.6) показывает, что потери по времени p_t, численно равные условным потерям p(γ>0), μогут быть определены и с помощью таблиц первой формулы Эрланга [17]. Используя эти таблицы, p_t можем определить из следующего соотношения:

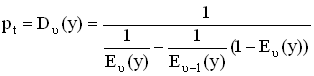, (3.12)

Потери измеряются в процентах или в промилле [0.1%].

Нормативы:

На ГТС между двумя ТА на одной ГТС р ≤ 0.03; на ЗТС между двумя ТА разных местных сетей одной зоны р ≤ 0.03 – 0,13; на МТС между двумя ТА разных зон семизначной нумерации р ≤ 0.1.

Если потери меньше 10 %, то абоненты на них не реагируют.

Основная задача инженерных расчетов – установление оптимального количества обслуживающих приборов при заданной интенсивности нагрузки и качестве обслуживания:

V = f [Y,р].