В алгебре логике различные логические выражения могут иметь только два значения: «истинно» или «ложно». Для обозначения истинности или ложности пользуются символами 1 и 0.
В алгебре логики используются функции вида Y=f(X1, Х2, ..., Хn), где сама функция и ее аргументы могут принимать лишь два дискретных значения 1 и 0. Если имеется n аргументов (логических переменных), то они образуют 2n возможных логических наборов из 1 и 0. Для каждого набора переменных логическая функция Y может принимать значение 0 или 1. Поэтому для n переменных можно образовать N=22n различных функций. Например, при n= 1 получим четыре булевых функции: f0(X) = 0 — постоянный 0; f1(Х) = Х — тождественность X; f2(Х)=Х —инверсия X; f3(X)= 1 — тождественность 1.
Все возможные логические функции n переменных можно образовать с помощью треx основных операций; логического отрицания (инверсии, операции НЕ), логического сложения (дизъюнкции, операции ИЛИ), логического умножения (конъюнкции, операции И).
Ниже приведены математические записи основных аксиом и законов булевой алгебры. Применение данных аксиом и законов позволяет производить упрощение логических функций. Логические функции могут иметь различные формы представления: словесное, табличное, алгебраическое, графическое. Наиболее широко используют представление функций в виде таблиц истинности. Таблица истинности содержит все возможные наборы значений логических переменных и значения функций, соответствующих каждому из наборов.
Aксиомы:: Законы:
1+х=1 х1+х2=х2+х1
0·х=0 х1·х2=х2·х1
0+х=х х1+х2+х3=(х2+х3)+ х1
1·х=х х1·х2·х3=(х2·х3)· х1
х+х=х х1·(х2+х3)=(х2·х1)+(х1·х3)
х·х=х х1+(х2·х3)=(х2+х1)·(х1+х3)
х+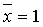 
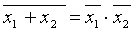
х·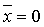 
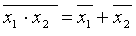
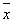=х х1+х1·х2= х1
х1·(х1+х2)= х1
Как было уже указано, любую логическую функцию можно представить с помощью соответствующей комбинации простейших логических функций И, ИЛИ, НЕ. Поэтому такой набор называют логическим базисом или функционально полным.
Используя законы булевой алгебры, нетрудно доказать, что функционально полными наборами также являются логические функции И, НЕ, ИЛИ, а также наборы из одной функции И-НЕ, ИЛИ-НЕ. Функциональная полнота этих наборов следует из того, что с их помощью можно реализовать все другие функции логических базисов.
Ниже рассматриваются электронные схемы, выполняющие простейшие логические операции. Для реализации цифровых систем любой сложности достаточно иметь набор логических элементов, реализующих операции хотя бы одного из функционально полных наборов. Этот набор элементов называют минимальной базой. В современной микроэлектронике такой базой являются элементы либо И-НЕ, либо ИЛИ-НЕ, выполняемые по различным технологиям на основе биполярных и полевых транзисторных структур.