1.6.1. Импульсная характеристика
1.6.2. Частотная передаточная функция
После того как мы разработали набор моделей для сигнала и шума, рассмотрим характеристики систем и их воздействие на сигналы и шумы. Поскольку систему с равным успехом можно охарактеризовать как в частотной, так и во временной области, в обоих случаях были разработаны методы, позволяющие анализировать отклик линейной системы на произвольный входной сигнал. Сигнал, поданный на вход системы (рис. 1.9), можно описать либо как временной сигнал, 
, либо через его Фурье-образ, 
. Использование временного анализа дает временной выход 
, и в процессе будет определена функция 
, импульсная характеристика, или импульсный отклик, сети. При рассмотрении ввода в частотной области мы должны определить для системы частотную характеристику, или передаточную функцию 
, которая определит частотный выход 
. Предполагается, что система линейна и инвариантна относительно времени. Также предполагается, что система не имеет скрытой энергии на момент подачи сигнала на вход.
Рис.1.9. Линейная система и её ключевые параметры
1.6.1. Импульсная характеристика
Линейная, инвариантная относительно времени система или сеть, показанная на рис. 1.9, описывается (во временной области) импульсной характеристикой , представляющей собой реакцию системы при подаче на ее вход единичного импульса 
.
при 
(1.45)
Рассмотрим термин «импульсный отклик», крайне подходящий для данного события. Описание характеристик системы через ее импульсный отклик имеет прямую физическую интерпретацию. На вход системы мы подаем единичный импульс (нереальный сигнал, имеющий бесконечную амплитуду, нулевую ширину и единичную площадь), как показано на рис. 1.10, а. Подачу такого импульса в систему можно рассматривать как «мгновенный удар». Как отреагирует («откликнется») система на такое применение силы (импульс)? Выходящий сигнал - это и есть импульсный отклик системы. (Возможный вид этого отклика показан на рис. 1.10, б.)
Отклик сети на произвольный сигнал является сверткой с , что записывается следующим образом.
(1.46)
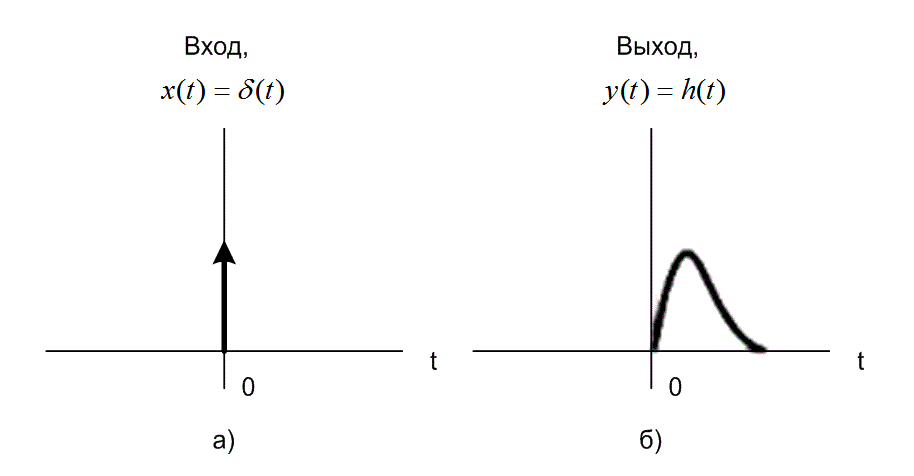
Рис.1.10. Иллюстрация понятия «импульсный отклик»: а) входной сигнал является единичной импульсной функцией; б) выходной сигнал - импульсным откликом системы
Здесь знак «*» обозначает операцию свертки (см. раздел А.5). Система предполагается причинной, что означает отсутствие сигнала на выходе до момента времени 
, когда сигнал подается на вход. Следовательно, нижняя граница интегрирования может быть взята равной нулю, и выход можно выразить несколько иначе.
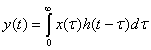(1.47,а)
или в виде
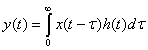(1.47,б)
Выражения в уравнениях (1.46) и (1.47) называются интегралами свертки. Свертка (convolution) - это фундаментальный математический аппарат, играющий важную роль в понимании всех систем связи. Если читатель не знаком с этой операцией, ему стоит обратиться к разделу А.5, где приводится вывод уравнений (1.46) и (1.47).
1.6.2. Частотная передаточная функция
Частотный выходной сигнал получаем при применении преобразования Фурье к обеим частям уравнения (1.46). Поскольку свертка во временной области превращается в умножение в частотной (и наоборот), из уравнения (1.46) получаем следующее.
(1.48)
или
(1.49)
(Подразумевается, конечно, что 
для всех 
.) Здесь 
, Фурье-образ импульсного отклика, называемый частотной передаточной функцией, частотной характеристикой, или частотным откликом сети. Вообще, функция является комплексной и может быть записана как
, (1.50)
где 
- модуль отклика. Фаза отклика определяется следующим образом.
(1.51)
(
и 
обозначают действительную и мнимую части аргумента.)
Частотная передаточная функция линейной, инвариантной относительно времени сети может легко измеряться в лабораторных условиях - в сети с генератором гармонических колебаний на входе и осциллографом на выходе. Если входной сигнал выразить как
,
то выход можно записать следующим образом.
(1.52)
Входная частота 
смещается на интересующее нас значение; таким образом, измерения на входе и выходе позволяют определить вид 
.
1.6.2.1. Случайные процессы и линейные системы
Если случайный процесс формирует вход линейной, инвариантной относительно времени системы, то на выходе этой системы получим также случайный процесс. Иными словами, каждая выборочная функция входного процесса дает выборочную функцию выходного процесса. Входная спектральная плотность мощности 
и выходная спектральная плотность мощности 
связаны следующим соотношением.
(1.53)
Уравнение (1.53) предоставляет простой способ нахождения спектральной плотности мощности на выходе линейной, инвариантной относительно времени системы при подаче на вход случайного процесса.
В главах 3 и 4 мы рассмотрим обнаружение сигналов в гауссовом шуме. Основное свойство гауссовых процессов будет применено к линейной системе. Будет показано, что если гауссов процесс 
подается на инвариантный относительно времени линейный фильтр, то случайный процесс 
, поступающий на выход, также является гауссовым [6].
1.6.3. Передача без искажений
Что необходимо для того, чтобы сеть вела себя как идеальный канал передачи? Сигнал на выходе идеального канала связи может запаздывать по отношению к сигналу на входе; кроме того, эти сигналы могут иметь различные амплитуды (простое изменение масштаба), но что касается всего остального - сигнал не должен быть искажен, т.е. он должен иметь ту же форму, что и сигнал на входе. Следовательно, для идеальной неискаженной передачи выходной сигнал мы можем описать как
, (1.54)
где 
и 
- константы. Применив к обеим частям преобразование Фурье (см. раздел А.3.1), имеем следующее.
(1.55)
Подставляя выражение (1.55) в уравнение (1.49), видим, что необходимая передаточная функция системы для передачи без искажений имеет следующий вид.
(1.56)
Следовательно, для получения идеальной передачи без искажений общий отклик системы должен иметь постоянный модуль, а сдвиг фаз должен быть линейным по частоте. Недостаточно, чтобы система равно усиливала или ослабляла все частотные компоненты. Все гармоники сигнала должны поступать на выход с одинаковым запаздыванием, чтобы их можно было просуммировать. Поскольку запаздывание связано со сдвигом фаз 
и циклической частотой 
соотношением
, (1.57,а)
очевидно, что, для того чтобы запаздывание всех компонентов было одинаковым, сдвиг фаз должен быть пропорционален частоте. Для измерения искажения сигнала, вызванного запаздыванием, часто используется характеристика, называемая групповой задержкой; она определяется следующим образом.
(1.57,б)
Таким образом, для передачи без искажений имеем два эквивалентных требования: фаза должна быть линейной по частоте или групповая задержка 
должна быть равна константе. На практике сигнал будет искажаться при проходе через некоторые части системы. Для устранения этого искажения в систему могут вводиться схемы коррекции фазы или амплитуды (выравнивания). Вообще, искажение - это общая характеристика ввода-вывода системы, определяющая ее производительность.
1.6.3.1. Идеальный фильтр
Построить идеальную сеть, описываемую уравнением (1.56), нереально. Проблема заключается в том, что в уравнении (1.56) предполагается бесконечная ширина полосы, причем ширина полосы системы определяется интервалом положительных частот, в которых модуль 
имеет заданную величину. (Вообще, существует несколько мер ширины полосы; самые распространенные перечислены в разделе 1.7.) В качестве приближения к идеальной сети с бесконечной шириной полосы выберем усеченную сеть, без искажения пропускающую все гармоники с частотами между 
и 
где - нижняя частота среза, а - верхняя, как показано на рис. 1.11. Все подобные сети называются идеальными фильтрами. Предполагается, что вне диапазона 
, который называется полосой пропускания (passband), амплитуда отклика идеального фильтра равна нулю. Эффективная ширина полосы пропускания определяется шириной полосы фильтра и составляет 
Гц.
Если 
и 
, фильтр называется пропускающим (рис. 1.11, а). Если 
и имеет конечное значение, он именуется фильтром нижних частот (рис. 1.11, б). Если имеет ненулевое значение и 
, он называется фильтром верхних частот (рис. 1.11, в).
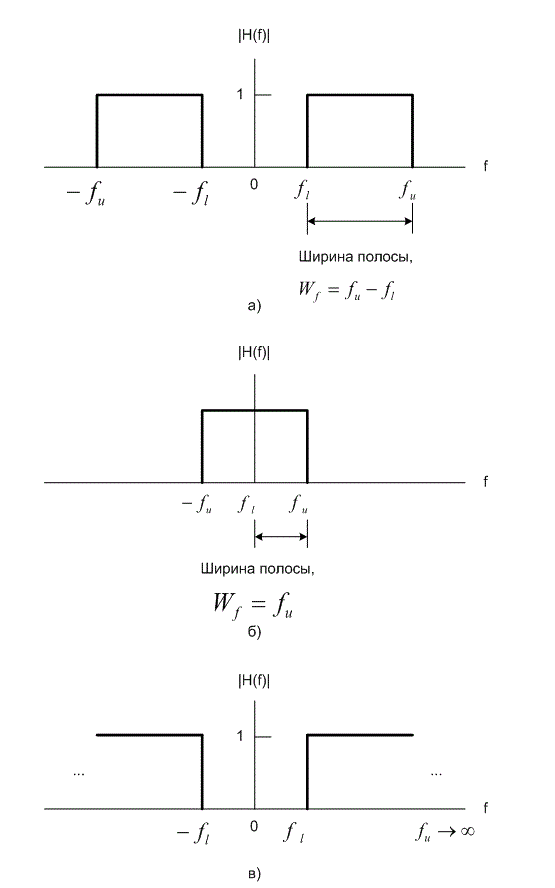
Рис.1.11. Передаточная функция идеальных фильтров: а) идеальный пропускающий фильтр; б) идеальный фильтр нижних частот; в) идеальный фильтр нижних частот
Используя уравнение (1.59) и полагая 
для идеального фильтра нижних частот с шириной полосы 
Гц, показанной на рис. 1.11, б, можно записать передаточную функцию следующим образом.
(1.58)
где
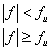(1.59)
и
(1.60)
Импульсный отклик идеального фильтра нижних частот, показанный на рис. 1.12, выражается следующей формулой.
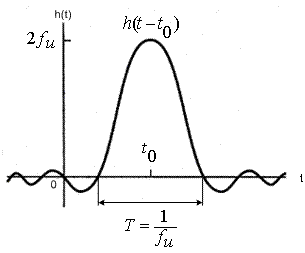
Рис.1.12. Импульсный отклик идеального фильтра нижних частот
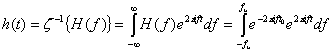(1.61)
или
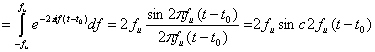, (1.62)
где функция 
определена в уравнении (1.39). Импульсный отклик, показанный на рис. 1.12, является непричинным; это означает, что в момент подачи сигнала на вход (
), на выходе фильтра имеется ненулевой отклик. Таким образом, должно быть очевидно, что идеальный фильтр, описываемый уравнением (1.58), не реализуется в действительности.
Пример 1.2. Прохождение белого шума через идеальный фильтр
Белый шум со спектральной плотностью мощности 
, показанный на рис 1.8, а, подается на вход идеального фильтра нижних частот, показанного на рис. 1.11, б. Определите спектральную плотность мощности 
и автокорреляционную функцию 
выходного сигнала.
Решение
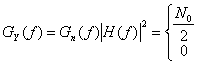
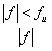
Автокорреляционная функция - это результат применения обратного преобразования Фурье к спектральной плотности мощности. Определяется автокорреляционная функция следующим выражением (см. табл. А.1).
Сравнивая полученный результат с формулой (1.62), видим, что имеет тот же вид, что и импульсный отклик идеального фильтра нижних частот, показанный на рис. 1.12. В этом примере идеальный фильтр нижних частот преобразовывает автокорреляционную функцию белого шума (определенную через дельта-функцию) в функцию 
. После фильтрации в системе уже не будет белого шума. Выходной шумовой сигнал будет иметь нулевую корреляцию с собственными смещенными копиями только при смещении на 
, где 
- любое целое число, отличное от нуля.
1.6.3.2. Реализуемые фильтры
Простейший реализуемый фильтр нижних частот состоит из сопротивления (R) и емкости (С), как показано на рис. 1.13, а; этот фильтр называется RC-фильтром, и его передаточная функция может быть выражена следующим образом [7].
, (1.63)
где 
. Амплитудная характеристика 
и фазовая характеристика изображены на рис. 1.13, б, в. Ширина полосы фильтра нижних частот определяется в точке половинной мощности; эта точка представляет собой частоту, на которой мощность выходного сигнала равна половине максимального значения, или частоту, на которой амплитуда выходного напряжения равна 
максимального значения.
В общем случае точка половинной мощности выражается в децибелах (дБ) как точка -3 дБ, или точка, находящаяся на 3 дБ ниже максимального значения. По определению величина в децибелах определяется отношением мощностей, 
и 
.
(1.64, а)
Здесь 
и 
- напряжения, a 
и 
- сопротивления. В системах связи для анализа обычно используется нормированная мощность; в этом случае сопротивления и считаются равными 1 Ом, тогда
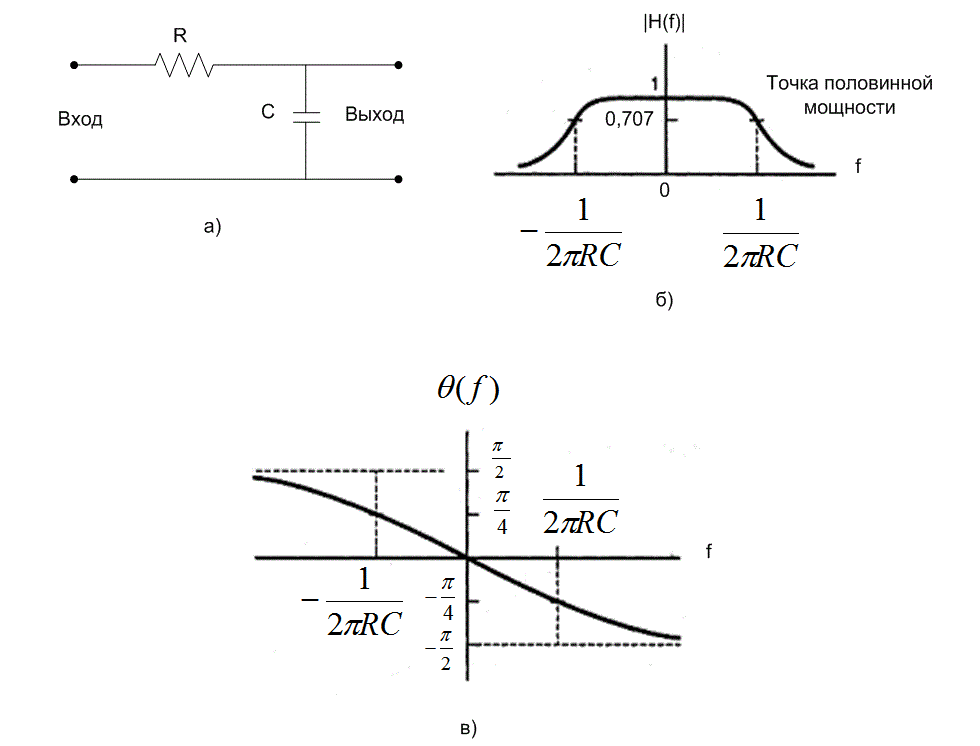
Рис.1.13. RC-фильтр и его передаточная функция: а) RC-фильтр; б) амплитудная характеристика RC-фильтра; в) фазовая характеристика RC-фильтра
(1.64, б)
Амплитудный отклик можно выразить в децибелах как
, (1.64, в)
где и - напряжения на входе и выходе, а сопротивления на входе и выходе предполагаются равными.
Из уравнения (1.63) легко проверить, что точка половинной мощности RC-фильтра нижних частот соответствует 
рад/с, или 
Гц. Таким образом, ширина полосы 
в герцах равна 
. Форм-фактор фильтра - это мера того, насколько хорошо реальный фильтр аппроксимирует идеальный. Обычно он определяется как отношение ширины полос фильтров по уровню -60 дБ и -6 дБ. Достаточно малый форм-фактор (около 2) можно получить в пропускающем фильтре с очень резким срезом. Для сравнения, форм-фактор простого RC-фильтра нижних частот составляет около 600.
Существует несколько полезных аппроксимаций характеристики идеального фильтра нижних частот. Одну из них дает фильтр Баттерворта, аппроксимирующий идеальный фильтр нижних частот функцией
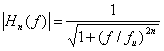
, (1.65)
где - верхняя частота среза (-3 дБ), а - порядок фильтра. Чем выше порядок, тем выше сложность и стоимость реализации фильтра. На рис. 1.14 показаны графики амплитуды для нескольких значений . Отметим, что по мере роста и амплитудные характеристики приближаются к характеристикам идеального фильтра. Фильтры Баттерворта популярны из-за того, что они являются лучшей аппроксимацией идеального случая в смысле максимальной пологости полосы пропускания фильтра.
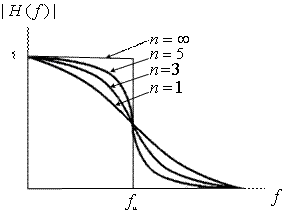
Рис.1.14. Амплитудный отклик фильтра Баттерворта
Пример 1.3. Прохождение белого шума через RC-фильтр
Белый шум со спектральной плотностью , показанной на рис. 1.8, а, подается на вход RC-фильтра, показанного на рис. 1.13, а. Найдите спектральную плотность мощности и автокорреляционную функцию сигнала на выходе.
Решение
Используя табл. А.1, находим Фурье-образ .
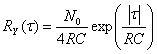
Как можно предположить, после фильтрации у нас уже не будет белого шума. RC-фильтр преобразовывает входную автокорреляционную функцию белого шума (определенную через дельта-функцию) в экспоненциальную функцию. Для узкополосного фильтра (большая величина RC) шум на выходе будет проявлять более высокую корреляцию между выборками шума через фиксированные промежутки времени, чем шум на выходе широкополосного фильтра.
1.6.4. Сигналы, каналы, спектры
Сигналы описываются через их спектр. Подобным образом сети или каналы связи описываются через их спектральные характеристики или частотные передаточные функции. Как ширина полосы сигнала влияет на результат передачи сигнала через фильтр? На рис. 1.15 показаны два случая, представляющие для нас практический интерес. На рис. 1.15, а (случай 1) входной сигнал имеет узкий спектр, а частотная передаточная функция фильтра является широкополосной. Из уравнения (1.48) видим, что спектр выходного сигнала представляет собой простое произведение этих двух спектров. Можно проверить (рис. 1.15, а), что перемножение двух спектральных функций дает спектр с шириной полосы, приблизительно равной меньшей из двух полос (когда одна из двух спектральных функций стремится к нулю, произведение также стремится к нулю). Следовательно, для случая 1 спектр выходного сигнала ограничен спектром входного сигнала. Подобным образом в случае 2, где входной сигнал является широкополосным, а фильтр имеет узкополосную передаточную функцию (рис. 1.15, б), видим, что ширина полосы выходного сигнала ограничена шириной полосы фильтра; выходной сигнал будет профильтрованным (искаженным) изображением входного сигнала.
Воздействие фильтра на сигнал также можно рассматривать во временной области. Выход , получаемый в результате свертки идеального входного импульса (имеющего амплитуду 
и ширину импульса Т) с импульсным откликом RC-фильтра нижних частот, можно записать в следующем виде [8].
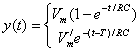
, (1.66)
где
(1.67)
Определим ширину импульса как
, (1.68)
а ширину полосы RC-фильтра как
. (1.69)
Идеальный входной импульс и его амплитудный спектр 
показаны на рис. 1.16. RС-фильтр и его амплитудная характеристика показаны на рис. 1.13, а, б. На рис. 1.17 показаны три примера, в каждом из которых использованы уравнения (1.66)-(1.69). Пример 1 иллюстрирует случай 
.
Отметим, что выходной отклик является достаточно хорошим приближением исходного импульса , показанного пунктиром.
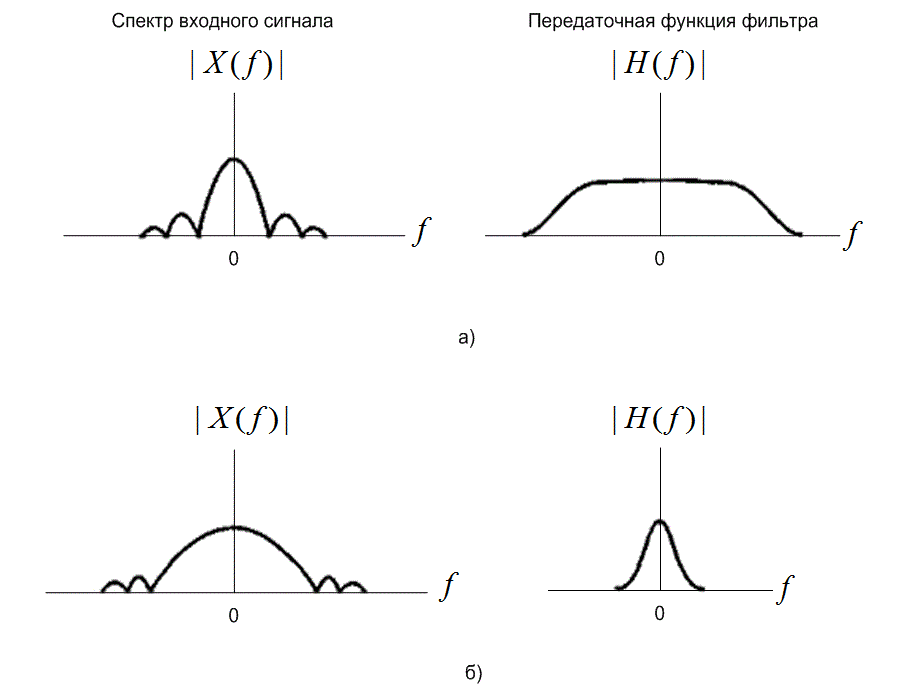
Рис.1.15. Спектральные характеристики входного сигнала и вклад цепи в спектральные характеристики выходного сигнала: а) случай 1. Ширина выходной полосы ограничена шириной полосы входного сигнала; б) случай 2. Ширина выходной полосы ограничена шириной полосы фильтра
Этот случай является примером хорошей точности воспроизведения. В примере 2, где 
, переданный импульс все еще можно распознать. Пример 3 иллюстрирует случай, когда 
. Видим, что по форме импульс едва угадывается. Где может понадобиться большая ширина полосы (или хорошая точность воспроизведения), как в примере 1? Это могут быть дистанционные приложения большой точности, где на время прибытия импульса влияет расстояние, что требует импульсов с малыми временами нарастания. Какой пример демонстрирует двоичные приложения цифровой связи? Пример 2. Как указывалось ранее (рис. 1.1), одной из принципиальных особенностей двоичной цифровой связи является то, что требуется всего лишь точно почувствовать, к какому из двух возможных состояний принадлежит каждый принятый импульс. Пример 3 был включен для полноты обсуждения; в реальных системах подобные схемы не используются.