Модель дискретного сигнала вида (8.10) предполагает, что отсчетные значения аналогового (непрерывного) сигнала берутся на неограниченном интервале времени. Однако, на практике осуществить такую дискретизацию невозможно, т.е. реальные сигналы ограничены во времени и дискретизация проводится на конечном интервале времени, равном длительности сигнала .

Рассмотрим особенности спектрального представления дискретного сигнала, который задан на интервале своими отсчетами , взятыми соответственно в моменты времени . Очевидно, что полное число отсчетов равно .

При спектральном анализе дискретных сигналов ограниченной длительности полагают, что такой сигнал периодически повторяется, с периодом равным (рис. 8.3а). А это означает, что такой периодический сигнал может быть представлен рядом Фурье (тригонометрическим или комплексным). Поскольку спектр периодического дис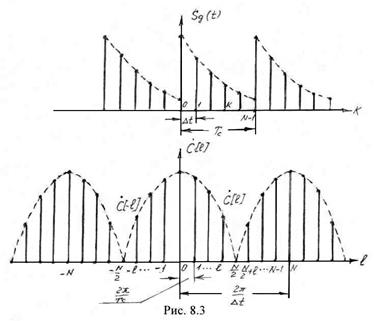 кретного сигнала, с одной стороны, является периодическим на оси частот с периодом , а спектр периодического на оси времени сигнала является линейчатым, следует ожидать, что спектр рассматриваемого ограниченного дискретного сигнала должен быть периодическим на оси частот и носить линейчатый характер. Действительно, для ограниченного во времени дискретного сигнала его представление (8.10) принимает вид

. (8.12)

Поскольку в соответствии с принятой методикой анализа является периодическим с периодом , разложим его в комплексный ряд Фурье

, (8.13)

где ; .

Комплексные амплитуды для рассматриваемого случая вычисляются следующим образом

. (8.14)

Подставляя (8.12) в (8.14), получим

.

Вводя безразмерную переменную и изменяя порядок суммирования и интегрирования, получим

.

И наконец, учитывая фильтрующее свойство -функции, окончательно приходим к результату

. (8.15)

Ввиду того, что является постоянной величиной, ее в (8.15) можно опустить и пользоваться только номерами отсчетов (8.15) принимает вид

. (8.16)

Выражение (8.16) является прямым дискретным преобразованием Фурье (ДПФ) и представляет собой алгоритм вычисления спектральных коэффициентов при известных значениях отсчетов . При этом, вычисления проводятся с использованием математических операций сложения, умножения и задержки средствами ЭВТ.

Совокупность представляет собой дискретный спектр периодического дискретного сигнала. На рис. 8.3б изображена спектральная функция дискретного сигнала. Как и предполагалось, спектральная функция является периодической с периодом , поскольку периодическим является сомножитель в (8.16) и дискретный сигнал также рассматривается как периодический (значения аргумента повторяются через каждые отсчетов). При этом, если число отсчетов дискретного сигнала четное, то первые значений составляющих соответствуют положительным частотам, а последующие значений , а также – отрицательным частотам (рис. 8.3б). Очевидно, что .

В дальнейшем удобно представлять дискретный сигнал в виде дискретной последовательности отсчетов . Тогда, в качестве периода дискретного сигнала выступает значение числа отсчетов и последовательность является периодической с периодом . Аналогично и спектральная функция является дискретной по оси частот последовательностью с тем же периодом .

Наряду с прямым ДПФ существует и обратное преобразование Фурье

. (8.17)

Обратное ДПФ позволяет рассчитать последовательность отсчетных значений , т.е. дискретный сигнал, если известна его спектральная функция в виде совокупности значений . Очевидно, обратное ДПФ приводит к периодической временной функции с периодом в отсчетов.

Отметим важное для практического использования ДПФ обстоятельство. При выводе (8.16) предполагалось, что дискретный сигнал представляет собой периодическую функцию времени. Вместе с тем на практике дискретный сигнал определен на интервале или на интервале . Вне этого интервала отсчетные значения равны нулю, однако и в этом случае выражения (8.16) и (8.17) справедливы для расчетов. Действительно, последовательность отсчетов , определенных на интервале , можно рассматривать как только один период соответствующей периодической последовательности и значения , рассчитанные в соответствии с (8.16) следует считать равными нулю вне интервала . Аналогично, обстоит дело и при вычислении значений по формуле (8.17).

Рассмотрим некоторые свойства ДПФ. Для краткости записи пару ДПФ будем представлять в виде

.

1. Линейность ДПФ. Пусть и два дискретных сигнала длиной отсчетов, а и – постоянные коэффициенты. Тогда

. (8.18)

2. Свойство временного сдвига. Если дискретному сигналу соответствует ДПФ , то

, (8.19)

т.е. сдвиг дискретного сигнала на интервалов приводит к изменению только его фазового спектра. Отметим, что временной сдвиг для дискретной последовательности представляет собой, так называемый круговой сдвиг. При круговом сдвиге значения отсчетов в зависимости от знака поочередно переносятся в начало или конец последовательности . Так, например, круговой сдвиг последовательности на интервалов при приводит к последовательности

,

т.е. отсчетов поочередно переносятся в конец последовательности.

3. Свойство симметрии. Это свойство фактически было уже рассмотрено выше при анализе спектральной функции (рис. 8.3б). Если – четное число, то свойство симметрии определяется следующим выражением

. (8.20)

Приведем некоторые соотношения, вытекающие из (8.16).

Спектральная составляющая

, (8.21)

является средним значением всех отсчетов.

Если – четное число, то

. (8.22)