Прежде чем преступить к рассмотрению дискретных цепей, отметим, что аналоговый сигнал может быть подвергнут цифровой обработке в соответствии со структурной схемой, изображенной на рис. 8.5.

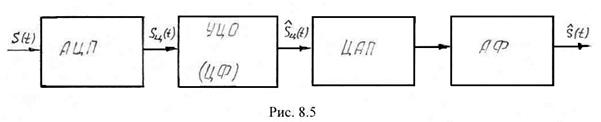
Входной аналоговый сигнал при помощи аналого-цифрового преобразователя преобразуется в цифровой сигнал . Цифровой сигнал поступает в устройство цифровой обработки (УЦО), представляющее собой вычислительное устройство. В УЦО производится обработка по заданному алгоритму, включающему арифметические операции сложения, умножения, а также операцию задержки во времени. Эти операции выполняются средствами ЭВТ, поэтому в качестве УЦО выступают специализированные ЭВМ.

Среди разнообразных алгоритмов обработки цифровых сигналов наибольшее распространение получила цифровая фильтрация, включающая в себя цифровой спектральный анализ. Поэтому в дальнейшем под УЦО будем подразумевать цифровой фильтр (ЦФ). На выходе ЦФ формируется новый сигнал , который после цифро-аналогового преобразования и прохождения через аналоговый фильтр является сигналом прошедшим цифровую обработку.

Цифровые сигналы, обрабатываемые в ЦФ дискретны во времени и квантованы по уровню. Кроме того все коэффициенты математических операций также квантованы. Учет квантованности сигналов и коэффициентов усложняет анализ цифровых систем. Поэтому для упрощения анализа полагают, что входные сигналы, подвергаемые цифровой обработке, дискретизированы по времени, но не квантованы (шаг квантования бесконечно мал) и предполагается, что коэффициенты фильтра могут принимать любые значения в заданном диапазоне. В этом случае УЦО может быть представлено в виде дискретной цепи, которая осуществляет операцию преобразования одной дискретной последовательности в другую.

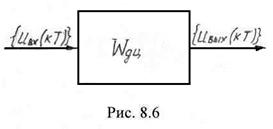
Придерживаясь методике анализа и обозначений непрерывных цепей будем в общем случае представлять дискретную цепь в виде «черного ящика» (рис. 8.6), на вход которого поступает входная дискретная последовательность

,

где принимает значения от до , а представляет собой промежутки времени между соседними отсчетами последовательности, и на выходе формируется выходная последовательность . Дискретная последовательность (входная или

выходная) математически описывается в виде набора чисел

. (8.27)

Поскольку промежутки времени между значениями последовательности одинаковы, то этот параметр при описании дискретной последовательности часто опускают

. (8.28)

Так же, как и непрерывные, дискретные цепи могут быть линейными и нелинейными. Дискретная цепь является линейной, если

, (8.29)

где – оператор преобразования дискретной цепи.

Аналогично непрерывным цепям дискретные цепи могут быть с постоянными или переменными параметрами.

Если ,

то для цепи с постоянными параметрами

,

т.е. задержка во времени входной последовательности на тактов приведет к такой же задержке и выходной последовательности. Поскольку в практике цифровой обработки подавляющее распространение получили линейные цепи с постоянными параметрами, именно этому классу цепей будет уделено основное внимание.

Дискретные линейные цепи можно описать уравнениями, связывающими входной и выходной сигналы. В отличие от непрерывных линейных цепей, которые описываются линейными дифференциальными уравнениями, дискретные цепи описываются линейными разностными уравнениями.

В качестве примера рассмотрим дискретный аналог непрерывной – цепи первого порядка, которая описывается уравнением:

, (8.30)

где – постоянная времени цепи.

При описании дискретной цепи производная по времени заменяется конечной разностью:

.

Тогда с учетом этого, после несложных преобразований можно получить

, (8.31)

где ; .

Выражение (8.31) представляет линейное разностное уравнение первого порядка, описывающее дискретный аналог непрерывной –цепи.

В общем случае дискретная линейная цепь описывается линейным разностным уравнением -го порядка

. (8.32)

Таким образом, уравнение (8.32) определяет очередной -тый отсчет выходного сигнала с учетом предыдущих значений выходного сигнала и предыдущих значений входного сигнала и полностью описывает дискретную линейную цепь.