Схема фильтра по методу частотной выборки строится с таким расчетом, чтобы коэффициенты фильтра соответствовали частотным отсчетам частотной характеристики.

а) Схема фильтра получается путем эквивалентных преобразований передаточной функции нерекурсивного фильтра.

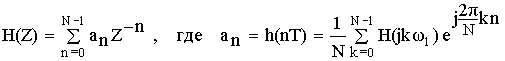
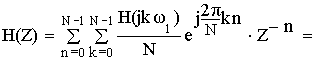
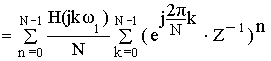
Применим :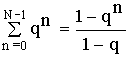

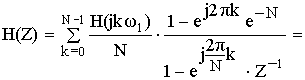
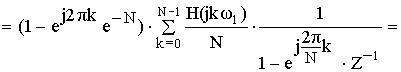
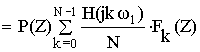
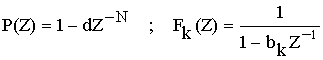
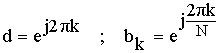
В соответствии с полученным результатом схема нерекурсивного фильтра примет следующий вид:

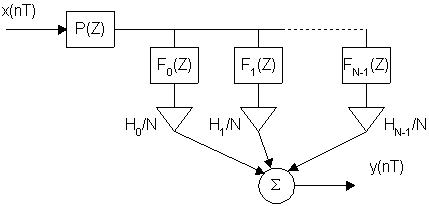
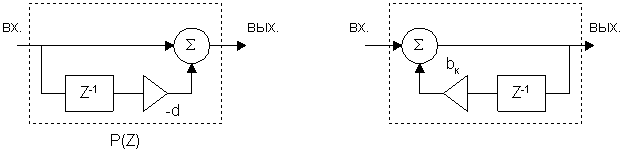
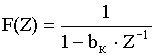
Нули и полюсы полученной передаточной функции 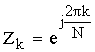совпадают и расположены на единичной окружности плоскости Z. Чтобы исключить возможность самовозбуждения, нули и полюсы целесообразно сместить внутрь единичной окружности на малую величину.

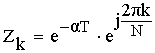– новое положение нуля и полюса.

Требуемое смещение нулей и полюсов функции получаем за счет некоторого изменения коэффициентов dи b_K.

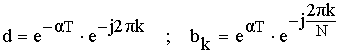
b) Частотная характеристика фильтра.

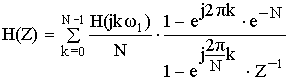
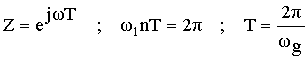
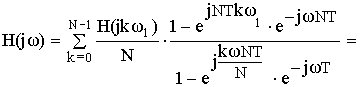
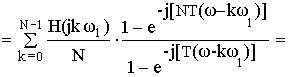
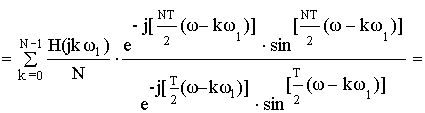
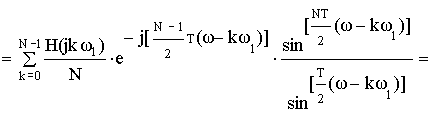
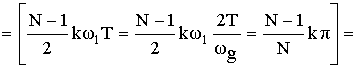
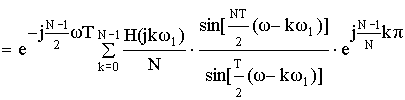
Частотная характеристика фильтра по методу частотной выборки получилась в форме ряда Котельникова для спектров дискретных сигналов, т.е. частотная характеристика состоит из суммы отсчетных функций, причем регулировка амплитуды каждой из отсчетнной функции не влияет на амплитуду других отсчетных функций.

Рассмотрим формирование суммы отсчетных функции на примере некоторой АЧХ.

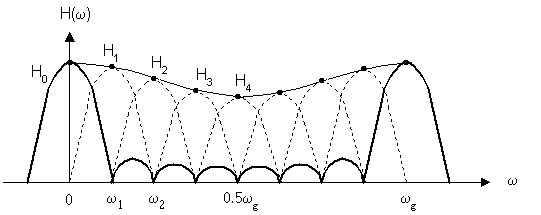
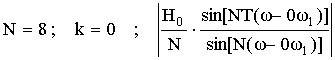
в) Схема фильтра с вещественными отводами.

Передаточная функция отводов k и N-k является комплексно-сопряженной, потому что частотная характеристика удовлетворяет условию комплексно-сопряженной симметрии.

Объединяя отводы k и N-k, мы получим один отвод с вещественными коэффициентами.

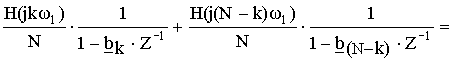
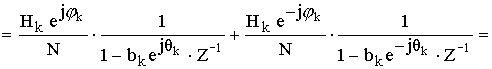
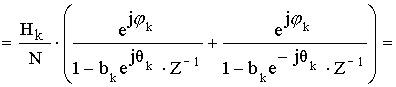
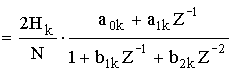
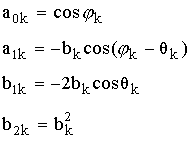
Полученному выражению соответствует схема:

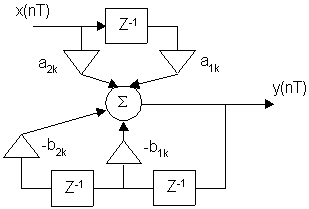
Схема с вещественными отводами получила преимущественное распространение. Важное достоинство: в схеме фильтра отсутствуют комплексные отводы соответствующие нулевым значениям требуемой частотной характеристики.