Двухтоновый однополосный сигнал можно представить выражением:

i= I_mнcos (w-W)t + I_mб coswt,

или:

i= I_mб[m₁cos (w-W)t+coswt)] , (5.5)

где m₁- отношение амплитуд колебаний несущей I_mн и боковой I_mб двухтонового сигнала (рис.5.4^а и 5.4^б), т.е. .

Из рис.5.4^а видно, что огибающая такого сигнала описывается формулой:

i_Ω= ,

или:

i_W = I_mб …(5.6)

По этому закону изменяются огибающие всех меняющихся со звуковой частотой составляющих напряжений и токов в усилителе мощности однополосного сигнала. Из (5.6) видно, что максимальное значение огибающей равно:

I_Ωmax = I_mб= I_mб (1+m₁) …(5.7)

При сигнале класса Н3Е, когда m₁=1, I_Ωmax=2I_mб, т.е. максимальное значение огибающей в этом случае равно амплитуде однотонового сигнала (рис.5.4^а и 5.4^б).

Постоянная составляющая огибающей однополосного двухтонового сигнала, или – что правильнее – ее среднее значение за период низкой частоты, отличаются от постоянной составляющей огибающей при амплитудной модуляции, где она неизменна и равна амплитуде колебаний в режиме несущей частоты. Среднее значение огибающей при двухтоновом однополосном сигнале определяется выражением:

I_τ= I_mб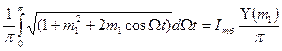 , (5.8)

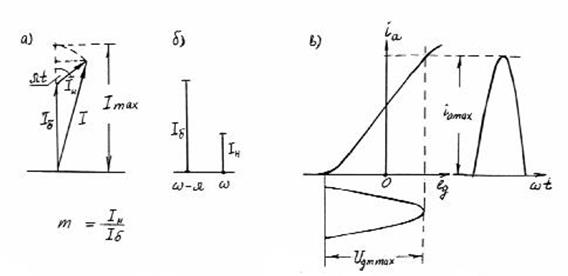
Рис.5.4

Значения интеграла Y(m₁) в зависимости от величины m₁ приведены на рис.5.5.

При двухтоновом сигнале класса Н3E m₁=1 и cредние значения всех составляющих напряжений и токов, меняющихся во времени со звуковой частотой, определяются формулой:

I_τ = I_mб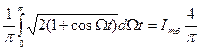 … (5.9)

Колебательная мощность двухтонового сигнала за период высокой частоты равна:

Р _~= ,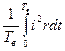

где Т_в - период высокой частоты w_, i - мгновенное значение тока, которое описывается (5.5). Подставляя сюда (5.5) и интегрируя, получим:

Р_~в = P_~б (1+m₁²+2m₁cosWt), …(5.10)

где Р_~б – мощность колебаний боковой частоты за период высокой частоты:

P_~б= … (5.11)

Мощность, отдаваемая в нагрузку за период низкой частоты (средняя мощность), равна:

Р_~τ= Р_~б 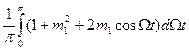. …(5.12)

После интегрирования получим:

Р_~τ= Р_~б(1+) …( 5.12’)

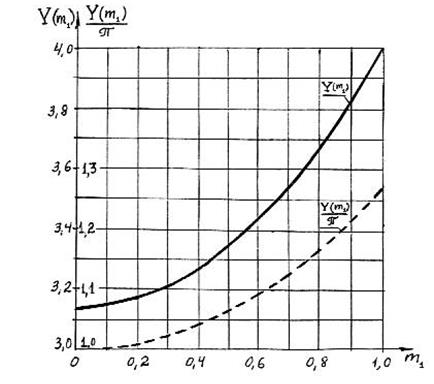
Рис.5.5

Из (5.10) следует, что пиковая мощность однополосного сигнала равна:

Р_~max = P_{~ б}(1+m₁)² , …(5.13)

а средняя мощность за период низкой частоты с учетом (5.13):

Р_~τ= Р_~б(1+)= Р_~max …(5.14)

При сигнале класса Н3Е, когда m₁=1:

Р_~max = 4P_~б , … ( 5.13’)

а

Р_~τ= 2Р_~б = 0,5 Р_~max … ( 5.14’)

Здесь P_~max представляет собой мощность однотонового сигнала с амплитутудой I_a1max = 2I_аmб – максимальной амплитудой первой гармоники анодного тока лампы, допускаемой ее колебательной характеристикой (рис.5.4^в), Р_~б – мощность колебаний боковой частоты, которая определяется (5.11).

По аналогии с (5.12) полная мощность, потребляемая лампой от источника питания, средняя за период низкой частоты, равна:

P_0τ=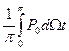 = E_aI_б0Y₁(m₁), …(5.15)

где Y₁(m₁)=Y(m₁)/p (рис.5.5).

Согласно рис.5.4 I_a0max= I_б0(m₁+1), т.е. I_б0= , тогда:

P_0τ=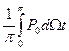 = E_aI_а0maxY₁(m₁)/(1+m₁). ( 5.15’)

При m₁=0 I_аmax= I_б ,а I_н=0 имеет место однополосный сигнал без несущей

(сигнал класса J3E).

Потери на аноде, средние за период низкой частоты, определяется выражением:

P_aτ = P_0τ – P_~τ,

Величина P_~τ определяется (5.14), а P_0τ – ( 5.15’).

Можно показать, что при двухтоновом сигнале класса Н3Е, когда m₁=1, потери на аноде наибольшие. При m₁=1 I_аб0=0,5I_а0max (рис.5.4). При этом:

Р_0t =0,5E_aI_а0maxY₁(m₁) = 0,5Р_0maxY₁(m₁)= P_0max …(5.16)

Здесь P_0max – значение мощности, подводимой к аноду лампы при однотоновом сигнале. Принимая во внимание (5.16) и ( 5.14’), получим:

Р_аτ = 0,5(1,27Р_0max – P_~max) , (5.17)

Следует отметить, что расчет режима генераторной лампы всегда производится для однотонового сигнала, т.е. на мощность P_~max.

Средние за период низкой частоты потери на управляющей сетке равны:

P_gτ = P_g~τ – P_g0τ ,

где Р_g~t - средняя за период низкой частоты мощность возбуждения, Р_g0t –средняя за период низкой частоты мощность, рассеиваемая в источнике сеточного смещения. По аналогии с ( 5.14’) для сигнала класса H3E:

P_g~t= 0,5P_g~max ,

где P_g~max - мощность возбуждения при однотоновом сигнале.

Средняя за период низкой частоты мощность, рассеиваемая в источнике смещения, равна:

P_g0τI_g0τ

и по аналогии с (5.16) при сигнале класса Н3Е:

P_g0t= P_g0max.

Тогда:

P_gτ=0,5(P_g~max–P_g0max) …(5.18).

При использовании тетрода средняя мощность рассеяния на экранной сетке при сигнале класса Н3Е определяется формулой:

P_g2t=Е_g2I_g20τ,

где Е_g2- напряжение на экранной сетке, а I_g20τ – среднее значение постоянной составляющей экранного тока. Принимая во внимание (5.9), получим:

P_g2t=Е_g2I_g20τ

Так как I_g20τ=0,5I_g2max, где I_g20max – постоянная составляющая экранного тока при однотоновом сигнале, то

P_g2t=Е_g2I_g20max ,

или:

P_g2t = ×P_g2max =0,637 P_g2max , …(5.19)

где P_g2max – мощность, рассеиваемая на экранной сетке при однотоновом сигнале.

Мощности тепловых потерь на электродах лампы не должны превышать допустимых значении.