2. Сигналы и помехи. Теория передачи сигналов

: Категория: Теория передачи сигналов

2.1. Определение и классификация сигналов

2.2. Сигнал как случайный процесс

2.3. Статистические характеристики флуктуационной помехи

2.4. Разложение сигнала на элементарные составляющие

2.5. Спектральное представление сигналов

2.6. Энергетический спектр сигнала

2.7. Временное представление сигналов. Теорема В. А. Котельникова

2.8. Аналитический сигнал

2.9. Линейное и нелинейное преобразования сигналов и помех

2.10. Геометрические представления сигналов

2.11. Различимость сигналов

2.1. Определение и классификация сигналов

Передача и хранение информации, т. е. перенос информации в пространстве и времени, осуществляются с помощью сигналов. В системах управления и связи обычно используются электрические сигналы. Физической величиной, определяющей такой сигнал, является напряжение (или ток), изменяющееся во времени по закону, отображающему передаваемое сообщение.

Сигналы можно классифицировать по ряду признаков. Один из таких признаков мы уже рассмотрели — это дискретность. По этому признаку различают дискретные и непрерывные сигналы, которые, в свою очередь, могут быть детерминированными или случайными. Различают также сигналы простые и сложные.

Сигнал называется детерминированным или регулярным, если его математическим представлением является заданная функция времени. С информационной точки зрения это означает, что под регулярным сигналом понимается такой сигнал, который соответствует известному сообщению. Такие сигналы не несут информации.

Сущность связи состоит в том, чтобы передать получателю не известные ему сведения. Сигналы, несущие такие сведения, на приемном конце заранее также будут неизвестными. Сигналы и тем более помехи для получателя являются случайными (недетермитнированными).

Необходимо подчеркнуть относительность понятия недетерминированности. Сигнал для отправителя на передающем конце детерминирован, так как три заданном способе передачи он определяется известным сообщением. Для получателя тот же сигнал недетерминирован, так как передаваемое сообщение на приемном конце неизвестно. Реальные сигналы, передаваемые по системам связи, как правило, обладают сочетанием свойств детерминированных и недетерминированных сигналов: некоторые параметры сигнала получателю известны заранее, а некоторые для него являются случайными.

Между сигналами и помехами нет принципиальной разницы. Помеха — это тоже сигнал, но нежелательный для данной системы или устройства. В ряде случаев одно и то же колебание для одной системы является сигналом, а для другой — помехой. Например, электромагнитные волны данной радиостанции являются полезным сигналом для приемников, которым предназначена передача этой радиостанции, и помехой для других приемников, работающих в том же диапазоне частот. Излучение космического объекта (звезды, например) является помехой радиоприему в диапазоне ультракоротких волн и вместе с тем полезным сигналом, несущим информацию о некоторых процессах, происходящих на этом космическом объекте.

Случайным сигналом мы будем называть сигнал, математическим описанием которого является случайная функция времени.

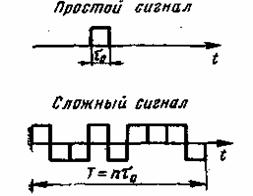
Рис. 2.1. Простой и сложный сигналы

В системах передачи дискретных сообщений каждый кодовый символ передается отрезком сигнала определенной длительности. to. Такой отрезок сигнала называется элементарным (простым) сигналом. В большинстве случаев элементарный сигнал представляет собой посылку постоянного тока, или отрезок гармонического колебания. Элементарный сигнал несет простейшую информацию, например, «да» или «нет», «плюс» или «минус». Сигнал, представляющий собой совокупность элементарных сигналов, называется составным или сложным (рис. 2.1).

В теории связи вводится понятие базы сигнала v. Она определяется как удвоенное произведение полосы частот сигнала на его длительность:

v=2TF (2.1)

Для простых сигналов vl, а для сложных v>>l. На этом основании простые сигналы часто называют узкополосными, а сложные — широкополосными.

Наконец, можно выделить так называемые эталонные или пробные сигналы. К ним относятся:

гармонический сигнал

f(t)=Acos(ωt+φ) () (2.2)

единичная функция (функция включения)

(2.3)

единичный импульс (дельта-функция)

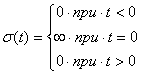
(2.4)

2.2. Сигнал как случайный процесс

В реальных условиях при передаче сообщений сигнал в точке приема заранее неизвестен и поэтому не может быть описан определенной функцией времени. То же самое можно сказать и о помехах, появление которых ,в канале может быть обусловлено самыми различными и чаще всего неизвестными для нас причинами.

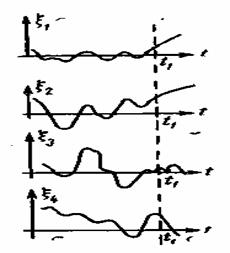
Рис. 2.2. Реализации случайного процесса

Таким образом, реальные сигналы и помехи представляют собой случайные процессы. Случайный процесс описывается случайной функцией, значения которой при любом значении аргумента являются случайными величинами. Аргументом функции может быть величина любой физической природы. Для электрических сигналов такой величиной обычно является время. При неизменных условиях опыта случайный процесс ξ(t) может принимать ту или иную конкретную форму ξ(t) (рис. 2.2). Эти возможные формы случайного процесса называются его реализациями. Совокупность всех возможных реализаций {ξ(t)} случайного процесса ξ(t) называется ансамблем. Реализации ξ(t) уже являются не случайными, а детерминированными функциями. Однако предсказать, какова будет реализация процесса в каждом конкретном опыте, невозможно.

Если рассматривать не каждую реализацию в отдельности, а совокупность их большого числа, то можно определить вероятностные характеристики случайного процесса. Такими характеристиками являются законы распределения, которые могут быть получены теоретически или на основе экспериментальных данных.

Пусть ξ(t) есть случайный процесс. В некоторый фиксированный момент времени t различные реализации процесса будут иметь различные значения (рис. 2.2). Значение является случайной величиной.

Одномерная функция распределения или интегральный закон распределения определяется как вероятность того, что случайная величина не превысит некоторого значения x.

F(x,t)= (2.5)

Частная производная

(2.6)

называется одномерной плотностью вероятности случайного процесса {ξ(t)} для t=t.

Двумерным интегральным законом распределения случайного процесса {ξ(t)} называется вероятность того, что в момент t функция {ξ(t)} не превысит некоторого значения x, а в момент — значения х2, т. е.

= (2.7)

Двумерная плотность вероятности определяется как частная производная (если она существует) второго порядка

(2.8)

Произведение выражает вероятность того, что в момент времени t функция ξ(t) находится в интервале между xи x+dx, а в момент времени — в интервале между х2и х2+dх2. Аналогично определяются трехмерный, четырехмерный, и т. д. законы распределения.

Наиболее полной характеристикой случайного процесса является n-мерный закон распределения, т. е. распределение значения ξ(t) для п произвольно выбранных моментов времени. Функция

(2.9)

называется n-мерным интегральным законом распределения, а частотная производная

(2.10)

называется n- мерной плотностью вероятности.

Случайный процесс задай, если его n-мерное распределение известно для любого числа n произвольно выбранных моментов времени .Если значения случайной функции l(t) при любых значениях t независимы, то

(2.11)

Отсюда следует, что исчерпывающей характеристикой случайной функции с независимыми значениями является ее одномерный закон распределения.

Законы распределения являются достаточно полными характеристиками случайного процесса. Однако они сложны и требуют для своего определения обработки большого экспериментального материала. Кроме того, такое подробное описание процесса не всегда бывает нужным. Для решения многих практических задач достаточно знать более простые (хотя и менее полные) характеристики случайного процесса. Такими характеристиками являются средние значения и функция корреляции случайного процесса.

(2.21)

В дальнейшем, говоря о стационарных процессах, мы будем иметь в виду стационарность в широком смысле.

Для стационарных процессов в большинстве практически важных случаев справедлива эргодическая теорема, согласно которой усреднение по ансамблю можно заменить усреднением по времени, т. е. с вероятностью, сколь угодно близкой к единице, можно считать:

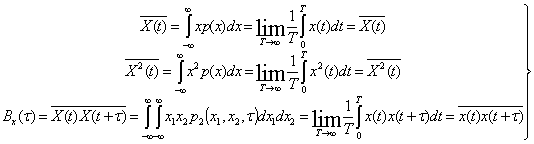(2.22)

Свойство эргодичности имеет большое практическое значение. Оно позволяет при исследовании статистических свойств процесса рассматривать не множество его реализаций, а всего лишь одну реализацию достаточно большой продолжительности. Например, при изучении свойств шума на выходе усилителя не нужно иметь большое число одинаковых усилителей, дающих различные реализации шума; достаточно взять один усилитель и исследовать шум на его выходе в течение длительного промежутка времени.

Важнейшей характеристикой эргодического процесса является его корреляционная функция. Поясним физический смысл этой функции. Пусть x(t) есть электрическое напряжение на выходе приемника. Если в момент t значение x(t) велико, то мало вероятно, что в момент t+τ, где τ — малая величина, оно станет очень малым. Если же взять τ достаточно большим, то величина x(t+τ) может быть уже какой угодно. Другими славами, между x(t) и x(t+τ) имеется зависимость, которая ослабевает с увеличением τ. Мерой этой зависимости может быть среднеквадратическое отклонение x(t) от x(t+τ),т. е.

Отсюда следует, что среднеквадратическое отклонение полностью определяется корреляционной функцией, которая указывает, насколько в среднем связаны друг с другом два значения эргодического процесса, разделенные интервалом времени τ.

Основными свойствами корреляционной функции являются следующие:

— автокорреляционная функция эргодического процесса является функцией четной, т. е. Bx(τ)= Bx(-τ)

— из определения (2.22) ясно, что Вх(0)==σ, т. е. значение корреляционной функции эргодического процесса при т=0 совпадает co средней мощностью этого процесса;

— любое значение корреляционной функции не может превышать значения этой функции при τ=0, т. е. Это вытекает из неравенства

я корреляционная функция не превосходит по модулю единицы: ρ(τ)1;

— если автокорреляционная функция процесса удовлетворяет условиям:

ВХ(0)0 при τ=0

Bx(τ)= 0 при |τ|>0,

то это означает, что между значениями x(t) и x(t+ τ) не существует связи. Taкиe процессы называют чисто случайными;

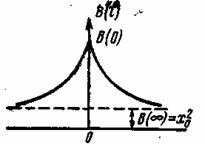
Рис. 2.3. График корреляционной функции эргодического процесса

— если эргодический процесс не содержит детерминированной составляющей, то его корреляционная функция неограниченно убывает с увеличением τ, т. е. зависимость между значениями x(t) и х(t+ τ) ослабевает и в пределе (при τ) они становятся независимыми. Наличие постоянной (детерминированной) составляющей в процессе x(t)=ξ(t)+x приводит к тому, что

На рас. 2.3 приведена типичная кривая корреляционной функции эргодического процесса, иллюстрирующая перечисленные свойства этой функции;

—функция автокорреляции периодического процесса есть периодическая функция с периодом этого процесса. Пусть имеется периодический процесс x(t)=

Тогда, в силу периодичности x(t), беря среднее за период, имеем

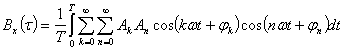
Ввиду того что интегралы от произведения косинусов при nk равны нулю, а n=k0 при эти интегралы равны — получаем

(2.23)

Заметим, что корреляционная функция не зависит от фазовых углов гармоник исходного периодического процесса.

Для случайного процесса, не содержащего детерминированных составляющих, можно указать такой интервал Δτ, что при τ>Δτ взаимная связь между значениями x(t) и x(t+ τ) будет несущественной (их можно считать некоррелированными). Этот интервал называется интервалом корреляций. Его обычно определяют шириной основания прямоугольника единичной высоты, площадь которого равна площади, ограниченной кривой коэффициента корреляции и осью абсцисс:

(2.24)

В ряде случаев случайный процесс представляет собой дискретную последовательность элементов (i=l, 2, . . ., п). Статистические свойства такой последовательности описываются вероятностями появления отдельных элементов p(), P(), . . ., Р(ап), причем , т. е. элементы последовательности образуют полную совокупность. Вероятности P() определяются из опыта или задаются заранее и поэтому называются априорными (доопытными) .

Для многих реальных дискретных сигналов вероятность выбора отдельных элементов последовательности зависит от предшествующих элементов. Вероятность сложного события, состоящего в последовательном выборе двух элементов и , определяется совместной вероятностью

(2.25)

где — условная вероятность, т. е. вероятность появления символа за символом . Из выражения (2.25) следует известная в теории вероятностей формула Байеса

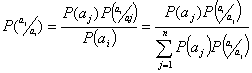(2.26)

Если вероятность появления отдельных элементов зависит от конечного числа элементов, предшествующих данному, то такая последовательность называется однородной сложной цепью Маркова. В частном случае, когда вероятность появления элемента зависит только от предшествующего элемента, цепь Маркова называется простой. Среди возможных цепей Маркова в теории передачи сигналов имеют большое значение эргодические цепи. Эргодичность означает статистическую однородность. Если процесс эргодический, то каждая последовательность, создаваемая процессом, имеет одинаковые статистические свойства. Если элементы в, и независимы, то P(,)=P()P() и P(/) = P().

2.3. Статистические характеристики флуктуационной помехи

Флуктуационная помеха представляет собой стационарный процесс с нормальным распределением вероятностей (гауссов процесс). Это непосредственно следует из центральной предельной теоремы теории вероятностей, согласно которой распределение суммы большого числа независимых случайных величин сходится к нормальному закону. Флуктуационная помеха, представляющая собой сумму большого числа независимых колебаний, удовлетворяет условиям этой теоремы.

Одномерная плотность вероятности гауссова процесса определяется следующим выражением:

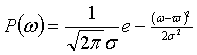(2.27)

где — среднее значение процесса, σ² — его дисперсия. Для флуктуационной помехи положительные и отрицательные значения ω встречаются одинаково часто и поэтому = 0. Дисперсия в этом случае равна средней мощности помех Р, а эффективное значение помехи UПЭ= Таким образом, плотность вероятности помехи приводится к виду

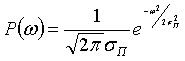(2.28)

Соответственно интегральная функция распределения

(2.29)

где u=ω/σ— относительное значение помехи:

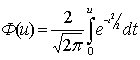(2.30)

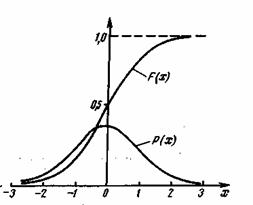
Рис. 2.4. Графики дифференциального и интегрального распределений гауссова процесса

Функция Ф(и) называется интегралом .вероятности или функцией Крампа. Значения этой функции приводятся в таблицах (см. приложение 1). Заметим, что функция Ф(и) является нечетной: Ф(-и)=-Ф(и), кроме этого, Ф()=1 и Ф(0)=0. На рис. 2.4 изображены графики дифференциального и интегрального распределений гауссова процесса.

Зная закон распределения вероятностей, легко найти вероятность того, что уровень помехи примет значение, лежащее в заданных пределах, например, между и . Очевидно,

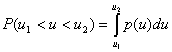
Подставляя р(и) согласно (2.28), находим

(2.31)

Вероятность того, что помеха превысит некоторый пороговый уровень и0, можно определить непосредственно из (2.31), если в последнем положить и :

(2.32)

Расчеты на основании (2.32) показывают, что вероятность превышения помехой порогового уровня быстро падает с увеличением . Так вероятность превышения уровня =1 равна 0,16, при 3 эта вероятность уже равна 0,0013, а при =4 она равна 3,5 и т. д. Отсюда следует, что колебания помехи практически не превышают трехкратного эффективного значения :помехи. Пикфактор помехи, определяемый как отношение максимального значения к эффективному, обычно лежит в пределах 3,5÷4,6. Поэтому флуктуационную помеху часто называют гладкой, в отличие от импульсных помех, для которых это отношение обычно много больше.

Двумерное распределение флуктуационной помехи имеет следующее выражение:

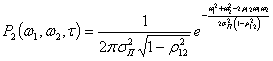(2.33)

Если помеха представлена последовательностью своих значений ωk=ω(tk) (k=1,2...), то ее исчерпывающим описанием будет n-мерное распределение

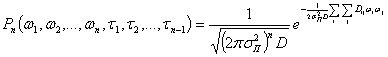(2.34)

где D — определитель п-го порядка корреляционной матрицы, а

— алгебраическое дополнение элемента . Здесь = коэффициент корреляции.

Из (2.34) следует, что гауссова функция распределения любого порядка содержит в качестве параметров только средние значения и моменты второго порядка (функцию корреляции), для нахождения которых достаточно знать лишь двумерную плотность вероятности, а тем самым и. Таким образом, нормальный случайный процесс вполне определяется заданием двумерной плотности вероятности.

Флуктуационная помеха называется белым шумом, если ее значения статистически независимы. В этом случае поэтому D=1, a

Следовательно, для белого шума n-мерный закон распределения согласно (2.34) будет

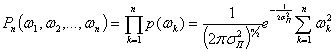(2.35)

Энергетический спектр такой помехи является равномерным (см. § 2.6). Следует иметь в виду, что понятие о белом шуме является идеализацией, так как энергетический спектр реальных процессов всегда убывает с частотой, а интервал корреляции имеет конечное значение Δτ0. Эта идеализация применима в тех случаях, когда интервал корреляции помехи много меньше постоянной времени системы, на которую она воздействует, или, иначе, когда в пределах полосы пропускания системы спектральную плотность помехи можно приближенно считать постоянной. В реальных системах эти условия обычно выполняются и помеху можно в первом приближении считать белым шумом.

Флуктуационный случайный процесс называется узкополосным, когда ширина спектра процесса относительно мала по сравнению со средней частотой этого спектра. Такого рода процессы имеют место на выходе схем, работающих на высоких и промежуточных частотах. Если смотреть на реализацию узкополосного процесса на экране осциллографа, то она будет иметь вид синусоиды с медленно меняющимися амплитудой (огибающей) и фазой. Мгновенные напряжения изменяются при этом со средней частотой спектра, а скорость изменения амплитуды определяется шириной спектра процесса. Процесс на выходе узкополосной системы внешне напоминает амплитудно-модулированное колебание со случайно изменяющимися огибающей и фазой. Аналитически узкополосный процесс можно представить в виде

(2.36)

где — средняя частота, U(t) и φ(t) — огибающая и фаза процесса — обе функции времени, медленно меняющиеся по сравнению с колебаниями на частоте .

Путем простого тригонометрического разложения (2.36) узкополосный процесс можно представить в виде суммы двух составляющих:

(2.37)

Здесь

U1(t) = U(t)cosφ(t) (2.38)

U(t) = U(t)sinφ(t) (2.39)

также являются медленно меняющимися функциями времени. Очевидно,

(2.40)

(2.41)

Если процесс (2.36) является гауссовым, то и его составляющие и будут иметь нормальное распределение с нулевым средним и дисперсией . В силу независимости составляющих и совместная плотность вероятности для одного и того же момента времени будет равна произведению одномерных плотностей вероятности и т. е.

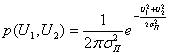(2.42)

Далее можно показать, что плотность вероятностей огибающей U узкополосного гауссова процесса определяется следующим выражением [6]:

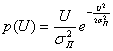
(2.43)

При расчетах вместо огибающей U удобно пользоваться ее нормированным значением z=U/.Подставив это значение в (2.43) и учитывая, что dz=, получим (2.44)

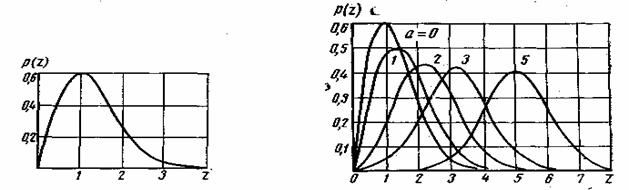
Рис. 2.5. Распределение Рэлея Рис. 2.6. Обобщенное распределение Рэлея

Это распределение известно под названием распределения Рэлея; его график изображен на рис. 2.5. Не следует путать распределение огибающей узкополосного нормального шума с распределением нормального широкополосного шума. В первом случае имеет место одностороннее, расположенное в положительной области, распределение Рэлея (рис. 2.5), а во втором — симметричное нормальное распределение (рис. 2.4).

Плотность вероятности фазы φ узкополосного гауссова процесса равномерна по всей области возможных значений φ :

(2.45)

В дальнейшем нам потребуются распределения вероятностей огибающей и фазы суммарного колебания гармонического сигнала s(t)=Acos и помехи ω(t). Если помеха представляет собой узкополосный гауссов шум, то согласно (2.37) суммарное колебание x(t) можно записать в виде

х(t)=s(t)+ω(t)= где

(2.46)

(2.47)

Плотность вероятности огибающей суммарного колебания сигнала и помехи в этом случае определяется следующим выражением:

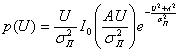(2.48)

где — модифицированная функция Бесселя нулевого порядка, — дисперсия помехи.

Распределение (2.48) называется обобщенным распределением Рэлея или распределением Раиса. При А=0 распределение (2.48) превращается в обычное распределение Рэлея (2.43).

Полагая и а=А/распределение Раиса можно записать в следующем виде:

(2.49)

На рис. 2.6. изображены графики этого распределения для различных значений где — мощность сигнала, — мощность помехи.

Выражение для плотности вероятности фазы суммарного колебания имеет следующий вид:

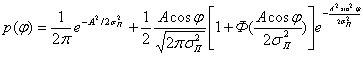(2.50)

где Ф(х) — функция Крампа (2.30).

2.4. Разложение сигнала на элементарные составляющие

В общем случае сигнал представляет собой сложное колебание, поэтому возникает необходимость представить сложную функцию s(t), определяющую сигнал, через простые функции. Простейшей с практической точки зрения формой выражения сигнала является линейная комбинация некоторых элементарных функций

(2.51)

При изучении линейных систем такое представление сигнала весьма удобно. Оно позволяет решение многих задач расчленить на части, применяя принцип суперпозиции. Например, чтобы определить сигнал на выходе линейной системы, вычисляется реакция системы на каждое элементарное воздействие (t), а затем результаты, умноженные на соответствующие коэффициенты ak складываются.

Функции (t) выбираются таким образом, чтобы любой сигнал можно было представить сходящейся суммой вида (2.51). Далее требуется, чтобы коэффициенты ak легко вычислялись и не зависели от числа членов суммы (2.51). Указанным требованиям наиболее полно удовлетворяет совокупность ортогональных функций.

Функции

(2.52)

заданные на интервале называются ортогональными, если

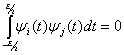при (2.53)

Интеграл от квадрата каждой функции семейства (2.52) равняется некоторой постоянной

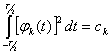(2.54)

Семейство функций

в силу (2.53) и (2.54) будет удовлетворять не только условию ортогональности, но и интеграл от квадрата каждой функции будет равен единице, т. е.

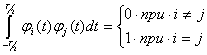(2.55)

Говорят, что функции семейства

(2.56)

ортогональны и нормированы (ортонормированны), если выполняются условия (2.55).

Пусть сигнал s(t) представлен в виде ряда по ортонормированным функциям (2.56):

(2.57)

где — некоторые числовые коэффициенты. Для определения коэффициентов умножим обе части равенства (2.57) на проинтегрируем по промежутку

(-T/2,T/2):

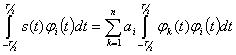
Принимая во внимание (2.55), получим

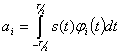(2.58)

Коэффициенты , определяемые по этим формулам, называются обобщенными коэффициентами Фурье, а ряд (2.57) при этом называют обобщенным рядом Фурье.

В теории связи для представления сигналов широко используются два частных случая разложения функций в ортогональные ряды: разложение по тригонометрическим функциям и разложение по функциям вида sinx/x. В первом случае получаем спектральное представление сигнала в виде обычного ряда Фурье, а во втором случае — временное представление в виде ряда В. А. Котельникова. Очевидно, оба эти представления адекватны (равносильны).

Для достаточной идентивности (точности) представления сигнала суммой (2.57) необходимо потребовать, чтобы

где ε — произвольная сколь угодно малая

положительная величина. Погрешность представления сигнала удобно оценивать средней квадратичной ошибкой

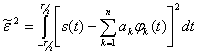(2.59)

Можно показать, что имеет наименьшее значение, если равны коэффициентам Фурье. В этом случае

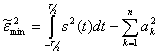(2.60)

Отсюда получаем неравенство

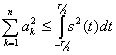(2.61)

При величина стремится к нулю и неравенство (2.61) превращается в известное равенство Парсеваля

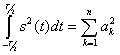(2.62)

-Г/2

Система ортонормированных функций (2.56) называется замкнутой, если справедливо равенство (2.62). Эта система будет называться полной, если к ней нельзя присоединить ни одной функции, ортогональной одновременно всем функциям (2.56) и не равной тождественно нулю. Из условия замкнутости функции следует и их полнота. Поэтому можно сказать, что равенство (2.62) является необходимым и достаточным условием полного представления некоторого класса сигналов совокупностью ортогональных функций {}

Случайный сигнал (или помеха), заданный на интервале (-Т/2,Т/2), может быть также представлен рядом (2.51) или (2.57). При этом коэффициенты будут случайными величинами, принимающими с определенной вероятностью значения, соответствующие различным реализациям сигнала (помехи).

2.5. Спектральное представление сигналов

Основой спектрального анализа сигналов является представление функции времени в виде ряда или интеграла Фурье. Любой периодический сигнал s(t), удовлетворяющий условию Дирихле, может быть представлен в виде ряда по тригонометрическим функциям

(2.63)

где ,

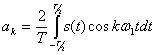(2.64)

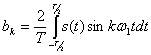(2.65)

Величина , выражающая среднее значение сигнала за период, называется постоянной составляющей. Она вычисляется по формуле

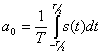(2.66)

Весьма удобной является комплексная форма записи ряда Фурье

(2.67)

где

Величина A есть комплексная амплитуда, она находится по формуле

A 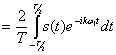(2.68)

Соотношения (2.67) и (2.68) составляют пару дискретных, преобразований Фурье. Необходимо отметить, что рядом Фурье можно представить не только периодический сигнал, но и любой сигнал конечной длительности. В последнем случае сигнал s(t) принимается периодически продолженным на всей оси времени. При этом равенство (2.63) или (2.67) представляет сигнал только на интервале его длительности (-T/2, T/2). Случайный сигнал (или помеха), заданный на интервале (-T/2, T/2), может быть также представлен рядом Фурье

(2.69)

где и являются случайными величинами (для флуктуационной помехой — независимыми случайными величинами с нормальным распределением). Тригонометрические функции

являются ортогональными на интервале (-T/2, T/2), но не являются нормированными. Ортонормированными будут следующие функции:

Учитывая это, обычный ряд Фурье (2.63) удобно записать в виде:

(2.70)

(2.71)

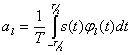
Коэффициенты в разложении (2.70) представляют собой эффективные значения составляющих спектра сигнала. Средняя мощность сигнала, выделяемая на сопротивлении 1 Ом,

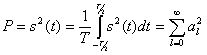(2.72)

Флуктуационную помеху ω(t) с постоянной интенсивностью также удобно представить рядом Фурье в форме, аналогичной (2.70):

(2.73)

где ξ — случайная величина, имеющая нормальное распределение вероятностей с нулевым средним значением и единичной дисперсией. Если сигнал ограничен полосой F, то ряд Фурье превращается в конечную тригонометрическую сумму

(2.74)

Число слагаемых, определяющих такой сигнал, равно его базе v=2TF, где — условная полоса частот, занимаемая сигналом.

Практически ширина спектра сигнала обычно определяется как область частот, в пределах которой сосредоточена основная энергия сигнала (например, 95%). Иногда эту полосу определяют также с учетом требования сохранения формы сигнала. Хотя условия одновременного ограничения длительности и полосы частот не могут быть выполнены в точности, однако можно ограничить спектр полосой F и иметь малые значения сигнала вне интервала Т.

Непериодический сигнал можно рассматривать как периодический с периодом . При этом разность частот между соседними гармониками стремится к нулю. Спектр становится сплошным, амплитуды — бесконечно малыми. Путем предельного перехода для представления непериодического сигнала получим интегральную пару преобразований Фурье:

(2.75)

Где S(iω)— спектральная плотность сигнала. Поскольку спектральная характеристика S(iω)— комплексная величина, то ее можно представить в виде

S(iω)=А(ω)+iВ(ω)=S(ω)е (2.76)

Модуль и фаза спектральной характеристики соответственно равны:

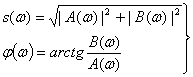(2.77)

Структура спектра непериодического сигнала полностью определяется функциями частоты S(ω) (спектром амплитуд) и φ(ω) (спектром фаз).

Для примера определим спектр колокольного импульса. Этот импульс выражается функцией

(2.78)

Замечательным свойством этой функции является ее инвариантность при преобразовании Фурье: спектр колокольного импульса представляет coбoй также колокольную кривую. Действительно, для спектра импульса (2.78) получаем

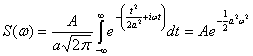(2.79)

Графики пары преобразований (2.78) и (2.79) приведены на рис. 2.7а и б.

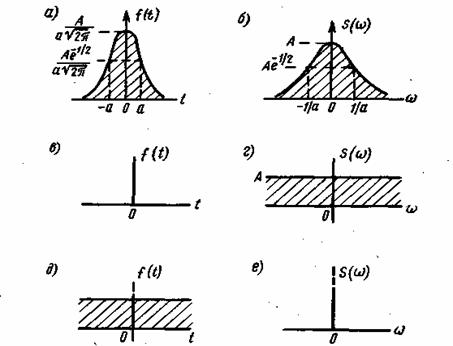
Рис. 2.7. Колокольный импульс и его предельные формы

Изменение параметра а на кривых этого рисунка показывает, что короткий импульс имеет широкий спектр, а длинный импульс — узкий спектр. Это свойство относится не только к данному примеру. Оно является общим положением, согласно которому ширина спектра любого процесса обратно пропорциональна его длительности. На рис. 2.7 в и г показаны предельные формы колокольных функций рис. 2.7а и б при малом параметре а. Здесь при а0 импульс вырождается в дельта-функцию, спектр которой является равномерным. При возрастании параметров А и а, когда их отношение остается постоянным, импульс превращается в постоянный сигнал — сигнал нулевой частоты (рис. 2.7 д и е).

2.6. Энергетический спектр сигнала

При наблюдении за течением случайного процесса мы можем определить лишь текущий спектр данной реализации x(t), т. е.

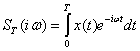(2.80)

Эта функция является случайной. Поэтому удобно ввести понятие энергетического спектра, которое приводит к неслучайной функции частоты.

Энергетический спектр стационарного случайного процесса определяется как спектр его функции корреляции.

(2.81)

Обратное преобразование Фурье дает

(2.82)

Так как B(τ) и G(ω) — четные, функции своих аргументов, то ф-лы (2.81) и (2.82) можно записать в другом виде:

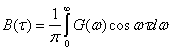(2.83)

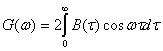(2.84)

Физический смысл функции G(ω) легко выяснить на основании (2.82), если в последнем положить τ=0. При этом мы получаем

(2.85)

где Р — полная мощность процесса.

Формула (2.85) показывает, что функция G(ω) выражает спектральную плотность мощности процесса. Мощность в полосе — можно определить интегрированием G(ω) в пределах от до , т. е.

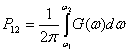
Энергетический спектр можно выразить и через текущий спектр реализации i(2.80). Согласно равенству Парсеваля энергия процесса x(t), выделяющаяся за время Т, равна:

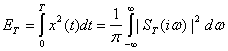(2.86)

Средняя мощность процесса определится как предел ЕТ/Т при , т. е.

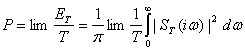(2.87)

Сопоставляя (2.85) и (2.87), находим

(2.88)

Это соотношение устанавливает связь между энергетическим спектром процесса и текущим спектром его реализации.

Энергетический спектр характеризует поведение реализаций процесса в среднем. Так, если спектр G(ω) сосредоточен в области низких частот, то процесс этот — медленно изменяющийся по сравнению с тем процессом, у которого спектр сосредоточен в области. более высоких частот. Для узкополосного процесса G(ω) заметно отличается от нуля только в полосе Δω вокруг средней частоты ) причем Δω<<. Такой процесс напоминает синусоиду с медленно меняющимися амплитудой и фазой.

Поскольку энергетический спектр и функция корреляции связаны между собой парой преобразований Фурье, то к ним можно применить известные теоремы спектрального анализа. Некоторые соотношения из этих теорем приведены в табл. 2.1. Здесь предполагается, что х=0, a и — независимы.

Случайный процесс, у которого G(ω)= — постоянная величина, называется белым шумом.

Таблица 2.1

Корреляционная функция белого шума согласно (2.82) равна:

(2.89)

Для случайных процессов имеет место связь общего характера между шириной спектра Δf, и интервалом корреляции Δτ:

(2.90)

где μ — постоянная порядка единицы. Интервал корреляции вычисляется на основании выражения (2.24). Ширина энергетического спектра определяется аналогичным соотношением

(2.91)

Пусть, например, задан процесс, функция корреляции которого определяется выражением . Энергетический спектр такого процесса согласно (2.84)

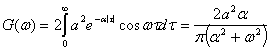
Далее, , а согласно (2.24). Затем отсюда .

2.7. Временное представление сигналов. Теорема В. А. Котельникова

Реальные сигналы всегда имеют конечную длительность и ограниченную полосу частот. Граничные частоты спектра определяются свойствами системы передаче и самим получателем. Так, при передаче дискретных сообщений полоса частот определяется скоростью передачи, при передаче телевизионного изображения — принятым стандартом четкости (числом строк) и т. д.

Для функций с ограниченным спектром В. А. Котельников доказал замечательную теорему, лежащую в основе дискретизации непрерывных сигналов. Согласно этой теореме функция f(t), не содержащая частот выше F, полностью определяется последовательностью своих значений в моменты, отстоящие друг от друга на , сек.

Доказательство теоремы состоит в следующем. Пусть функция f(t) имеет ограниченный спектр:

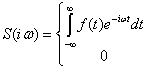
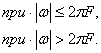
На конечном интервале .(-2πF,2πF) функцию S(iω) можно представить в виде ряда Фурье по аргументу ω. Согласно (2.67) имеем

Коэффициенты Фурье в этом случае запишутся в виде

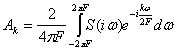
Так как S(iω) есть преобразование Фурье для f(t), то обратно f(t) есть преобразование Фурье для S(iω):

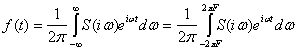
так как S(iω) равно нулю вне указанных пределов. Если положить t= получим

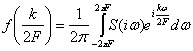
Сравнивая полученное выражение с выражением для , видим, что

Следовательно,

Так как f(t) однозначно определяется своим спектром S(iω), то из полученного соотношения следует, что f(t), как иS(iω), однозначно определяется отсчетами f(kΔt). Это и доказывает теорему Котельникова.

Выражая функцию f(t) через ее спектр S(iω), получим

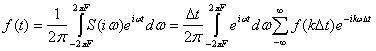
или, изменяя порядок действия,

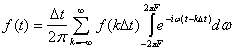
Отсюда после интегрирования находим

(2.92)

Полученное выражение представляет собой разложение непрерывной функции f(t) в ряд по ортогональным функциям вида Величины f(kΔt) называются отсчетами функции f(t). Они определяют значения исходной функции f(t) в дискретные моменты времени kΔt. Множитель называется функцией отсчетов. Если обозначить τ=t—kΔt, то функция отсчетов примет вид

(2.93)

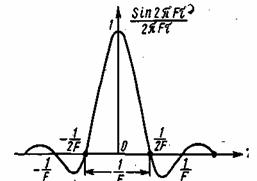
Рис. 2.8. Функция отсчетов

График этой функции приведен на рис. 2.8. Функция отсчетов принимает наибольшее значение, равное единице, в моменты времени t=kΔt(=0) и обращается в нуль в моменты времени t=(k±m)Δt где т-1,2, Ширина главного лепестка функции отсчетов на нулевом уровне равна 1/F. Спектр функции отсчетов является равномерным в полосе (-FdF,) и равен нулю вне этой полосы. Действительно,

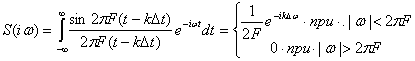
Модуль Энергия сигнала через отсчетные значения выражается следующим образом:

(2.94)

Если полоса частот сигнала f(t) неограниченно расширяется, то Δt будет неограниченно уменьшаться и в пределе при функция отсчетов стремится к дельта-функции), а ряд Котельникова (2.92) превращается в интеграл

(2.95)

Свертка дельта-функции с любой функцией f(t) дает равенство

из которого видно, что интеграл (2.95) не изменится от замены функции f(t) ее значением . Следовательно, (2.95) преобразовывается в интеграл Дюмеля, который обычно записывается

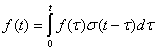(2.96)

Вернемся к выражению ряда Котельникова (2.92). Каждое слагаемое этого разложения по физическому смыслу представляет отклик идеального фильтра нижних частот, с частотой среза F на весьма короткий импульс, приходящий в момент и имеющий площадь, равную мгновенному значению функции f(t) в тот же момент. Отсюда следует, что при передаче сигнала f(t) с ограниченным спектром по каналу связи необходимо через равные интервалы Δt=1/2F взять отсчеты мгновенных значений сигнала и передать по каналу короткие импульсы, площади которых пропорциональны этим отсчетам. На приемном конце эти импульсы пропускаются через фильтр нижних частот и тем самым восстанавливается исходный сигнал f(t) как сумма откликов фильтра.

Сигнал конечной длительности Т, очевидно, будет определяться v== 2TF отсчетами. Строго говоря, не может существовать функции, ограниченной во времени и одновременно обладающей ограниченным спектром. Однако возможно существование функции, для которой почти вся энергия сосредоточена в конечном интервале времени ,и ограниченной полосе частот. Сигналы связи в большинстве случаев являются функциями такого типа. В этом случае разложение в ряд Котельникова будет давать некоторую погрешность ~, где Е — полная энергия сигнала и ΔE энергия той части спектра сигнала, которая расположена вне полосы F. При разложении сигнала в ряд Фурье мы тоже получили v=2TF. Таким образом, сигнал с ограниченным спектром F и конечной длительностью. Т определяется 2TF числами независимо от того, что собой представляют эти числа — мгновенные ли значения сигнала в точках отсчета либо спектральные коэффициенты разложения в ряд Фурье.

Теорема Котельникова позволяет единым образом рассматривать передачу любого сигнала (дискретного и непрерывного) как передачу чисел. Эта теорема лежит в основе всех видов импульсной модуляции. Согласно этой теореме необходимая частота следования импульсов F, называемая тактовой частотой, должна определяться из условия, где Fm — верхняя граничная частота спектра передаваемого сообщения.

Теорема Котельникова может быть обобщена и на случай функций, спектр которых не начинается с нулевой частоты. В формулировке автора эта теорема гласит: «Любую функцию f(t), состоящую из частот от f до f, можнo передавать с любой точностью при помощи чисел, передаваемых друг за другом через , сек. В этом случае функция f(t) на оси времени определяется через интервалы , где F=.При этом в каждой точке отсчитываются две величины: амплитуда и фаза. Если длительность сигнала равна Т, то количество отсчетных точек на оси времени

равно =TF, а общее количество отсчетов (амплитуд и фаз) равно v=2FT. Функцию f(t), ограниченную частотами f и f можно представить следующим рядом:

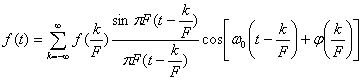(2.97)

где и отсчетные значения соответственно амплитуды и фазы сигнала;среднее значение круговой частоты спектра сигнала. Функция отсчетов в этом случае представляет собой модулированное колебание с несущей, равной , и огибающей, определяемой функцией вида

2.8. Аналитический сигнал

Реальные процессы описываются действительными функциями времени. Однако при рассмотрении многих задач удобно выражать сигнал в виде суммы элементарных сигналов, каждый из которых является комплексной функцией времени, либо рассматривать сам сигнал как комплексную функцию

(2.98)

где U(t) и ψ(t) — огибающая и фаза сигнала. Действительный сигнал s(t) в этом случае определяется следующим выражением:

(2.99)

Такое представление особенно удобно для узкополосных сигналов.

Сигнал называется «аналитическим», если s(t) и составляют пару преобразований Гильберта:

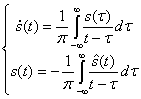(2.100)

Интегралы в этих соотношениях понимаются в виде главного значения Коши. Функция называется сопряженной с функцией по Гильберту. При таком выборе s(t) и огибающая и фаза сигнала определяются однозначно:

(2.101)

(2.102)

Если эффективная ширина спектра сигнала s(t) мала по сравнению с его средней частотой , то U(t) и ψ(t) изменяются медленно по сравнению с функцией s(t). Легко показать, что функции s(t)=cosωt соответствует сопряженная функция = sinωt, а функции s(t) =sinωt соответствует =сosωt. Если исходный сигнал представлен рядом Фурье s(t) =

то сопряженная ему функция будет

Таким образом, простейшему сигналу в виде гармонического колебания s(t)=Acosωt соответствует аналитический сигнал s(t)=Аcosωе+iФsinωе=Ae^iωt Если сигнал s(t) может быть представлен в виде интеграла Фурье s(t)=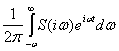, то частотный спектр сигнала будет

Спектры функций s(t) и связаны между собой следующим образом:

(2.103)

где sgn(ω)=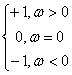

Таким образом, преобразование Гильберта сигнала s(t) можно рассматривать как результат прохождения s(t) через цепь, сдвигающую фазу всех частотных компонент спектра на угол — 90°. Частотная и переходная характеристики этой цепи таковы:

K(iω)=-isgn(ω),

h(t)=1/πt.

Подстановка выражения (2.103) в преобразование Фурье функции (2.98) показывает, что спектр S(iω) сигнала s(t) является «односторонним»:

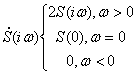(2.104)

Это очень полезное свойство аналитического сигнала.

Для периодических функций s(t) сопряженная по Гильберту

функция также является периодической с тем же периодом. Эти функции на отрезке, равном их периоду Т, взаимно ортогональны, т. е.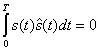

Сигналы s(f) и, для которых условие ортогональности сохраняется при замене одного из них на сопряженный по Гильберту, т. е. когда выполняются условия

(s,)= 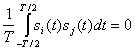(2.105)

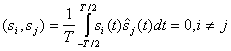
называются ортогональными в усиленном смысле. Можно показать, что такие сигналы также удовлетворяют и условию

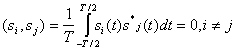(2.106)

где «звездочка» обозначает комплексно-сопряженную величину.

Введение понятия «аналитический сигнал» позволяет представить любую функцию времени (гари несущественных ограничениях) в комплексном виде и однозначно определить огибающую и фазу сигнала. В аналитической форме (2.98) могут быть представлены как детерминированные, так и случайные сигналы. Полезность такого представления состоит в возможности отдельного рассмотрения огибающей и фазы процесса (сигнала или помехи) . Так, при исследовании случайного процесса можно вместо изучения мгновенных значений ограничиться изучением огибающей и фазы процесса, а во многих случаях — либо огибающей, либо фазы.

В общем случае спектры и корреляционные функции процессов

x(t) и одинаковы: , Вх(ω) = .

Взаимный энергетический спектр равен =, а взаимная корреляционная функция, определяется выражением

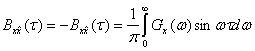. Между законом распределения случайного процесса x(t) с одной стороны и законами распределения огибающей U и фазы ψ с другой существует жесткая связь: зная закон распределения р(х), можно найти законы распределения p(U) и p(ψ). Сравнительно легко эта связь устанавливается в случае гауссовых процессов (см. § 2.3).

2.9. Линейное и нелинейное преобразования сигналов и помех

Рассмотрим линейную систему, импульсная реакция которой g(t) или коэффициент передачи К(iω) известны. Напомним, что К(iω) и g(t) связаны между собой преобразованием Фурье:

= £•

На вход системы поступает стационарный случайный сигнал x(t) с заданными характеристиками. На выходе системы получаем некоторый случайный сигнал y(t). Согласно теореме Дюамеля

y(t)=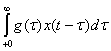 Найдем функцию автокорреляций сигнала

на выходе линейной системы

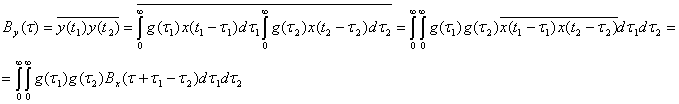(2.107)

где

Таким образом, By(τ) зависит не от и в отдельности, а от их разности т. Следовательно, при воздействии случайного стационарного процесса на линейную систему на выходе получается также стационарный случайный процесс y(t) с функцией корреляции, определяемой выражением (2.107).

Мощность выходного сигнала согласно (2.107) равна:

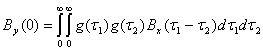(2.108)

Эта формула показывает, что для определения мощности выходного сигнала недостаточно знать В(0) входного сигнала — нужно знать всю функцию автокорреляции В(τ).

Связь между энергетическими спектрами сигнала на входе и выходе линейной системы может быть записана в виде

(2.109)

Действительно, согласно (2.82) и (2.107) имеем

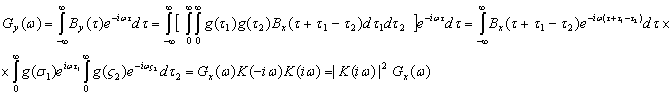
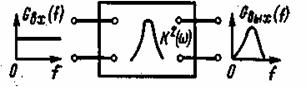
Рис. 2.9. Энергетический спектр шума на входе и выходе линейной системы

Из полученной формулы следует, что фазовая характеристика системы не оказывает влияния на энергетический спектр выходного сигнала. Пусть на вход линейной системы с коэффициентом передачи К(iω) воздействует белый шум с равномерным спектром gx(u) =(1/2)N0. Энергетический спектр выходного процесса согласно (2.109) будет gy(u) =(1/2)N0.Спектр помехи на выходе системы в этом случае повторяет по своей форме частотную характеристику системы с возведенными в квадрат ординатами (рис. 2.9). Мощность шума на выходе при этом равна:

(2.110)

Или, вводя эффективную полосу пропускания системы

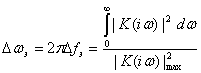(2.111)

получаем

(2.112)

Закон распределения вероятностей случайного процесса (сигнала или помехи) на выходе линейной системы в общем случае отличается от закона распределения вероятностей процесса на входе. В одном очень важном случае закон распределения при линейных преобразованиях не изменяется. Это — случай гауссова процесса. Если процесс на входе линейной системы имеет нормальное распределение, то он остается нормальным и на выходе. Изменяются только параметры процесса — дисперсия (мощность) и функция корреляции в соответствии с выражениями (2.107) и (2.108).

В случае узкополосной системы, когда полоса пропускания системы много меньше ширины спектра процесса на входе, имеет место явление нормализации закона распределения. Это явление состоит в том, что закон распределения процесса на выходе узкополосной системы сходится к нормальному независимо от того, Какое распределение имел процесс на входе. Физически это можно пояснить так. Отдельные возмущения на выходе системы, вызванные хаотическими воздействиями входного процесса, не успевая затухать, накладываются друг на друга и образуют новый процесс. Согласно предельной теореме вероятностей закон распределения этого процесса, представляющего собой сумму большого числа независимых случайных величин (возмущений), стремится к нормальному.

Рассмотрим теперь, как воздействует случайный процесс на нелинейную систему. В общем случае эта задача очень трудная. Дело обстоит значительно легче, когда речь идет о безинерционных нелинейных системах, в которых выходной процесс y(t) в данный момент однозначно определяется входным процессом x(t) в тот же момент времени. Пусть известны характеристика нелинейного устройства y=f(x) и статистические свойства входного процесса x(t). Необходимо определить статистические свойства выходного процесса y(t). В принципе, эта задача сводится к преобразованию переменных.

Рассмотрим простейший пример одномерной случайной величины. Известна плотность вероятности р(х) случайной величины х и нужно найти плотность вероятности р(у) случайной величины, у=S(х). Предположим, что существует однозначная обратная функция x=φ(y). Так как случайные величины связаны однозначной функциональной зависимостью, то из факта того, что х заключено в достаточно малом интервале (х0, х0+dx), следует, что величина и будет находиться в интервале (у0, у0+dy), где у0=f(x0). Следовательно, вероятности этих двух событий p(y)dy=p(x)dx, т. е.

(2.113)

Поскольку плотности вероятности не могут быть отрицательными, то в ф-лу (2.113) следует подставить модуль производной. Далее можно определить среднее значение выходного процесса (постоянную составляющую)

(2.114)

Аналогично определяются полная мощность процесса

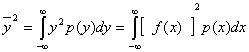(2. 115)

и функция корреляции

(2.116)

Энергетический спектр выходного процесса определяется с помощью преобразования Фурье от функции корреляции.

Спектр процесса на выходе нелинейной системы существенно отличается от спектра на входе вследствие появления новых частотных составляющих, которые отсутствовали во входном процессе. Спектр обычно содержит низкочастотные составляющие вблизи нулевой частоты и участки высокочастотных составляющих.

Таким образом, при воздействии случайного процесса на нелинейную систему изменяются спектр процесса, законы распределения вероятностей и все связанные с ними параметры процесса.

2.10. Геометрические представления сигналов

Совокупность трех чисел может быть представлена как координаты вектора в трехмерном пространстве. Аналогично n=2TF отсчетов, определяющих сигнал, можно представить себе как координаты вектора в воображаемом n-мерном пространстве.

Свойства n-мерного пространства в значительной степени являются обобщением свойств двух- и трехмерного пространства. Длина вектора x=() определяется его нормой ||х||:

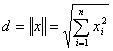(2.117)

Для сигнала s(t) квадрат длины вектора есть умноженная на 2F энергия соответствующего сигнала

(2.118)

непосредственно следует из равенства (2.94). Расстояние между двумя векторами х и у определяется как разности векторов

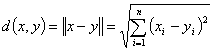(2.119)

Скалярное произведение двух векторов х и у:

(2.120)

Координаты векторов представляют собой проекции вектора х на оси. Если обозначить угол между двумя векторами через а, то получим выражения для

(2.121)

и для проекций х на у и обратно у на х:

Пространство непрерывных функций (сигналов), заданных на интервале 0<t<T, имеет бесконечное число измерений. Для такого пространства скалярное произведение двух векторов определяется соотношением

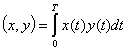(2.122)

а норма и расстояние между векторами:

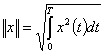(2.123)

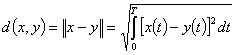(2.124)

Пространство с бесконечным числом измерений представляет собой естественное обобщение n-мерного пространства, получаемое путем предельного перехода от дискретной последовательности к функции непрерывного аргумента. Заметим, что нормы векторов сигналов равны корням из их энергии, а скалярное произведение является мерой корреляции этих сигналов.

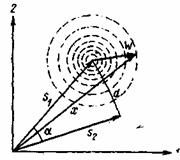
Рис. 2.10. Векторная диаграмма сигнала и помехи

Сигналы конечной длительности Т, ограниченные полосой F, геометрически представляются различными векторами в n-мерном пространстве. Различие между двумя какими-либо сигналами выражается расстоянием между векторами, изображающими их (рис. 2.10). Расстояние зависит от длин векторов и угла между ними, а косинус последнего согласно (2.121) есть не что иное, как коэффициент взаимной корреляции сигналов. Полное отсутствие корреляции (т. е. равенство нулю коэффициента корреляции) выражается ортогональностью векторов ().

Помеха, ограниченная той же полосой, что и сигнал, также определяется вектором из n-мерном пространстве. Этот вектор добавляется к вектору сигнала (рис. 2.10). В отличие от вектора сигнала, вектор помехи может иметь любые величину и направление (вектор является случайным). В результате при наложении помехи на сигнал вокруг конца вектора сигнала образуется «облако», переменная плотность которого выражает вероятность попадания результирующего вектора x=s+w (вектора принятого сигнала) в данный элемент объема. Для флуктуационной помехи это «облако» имеет сферическую форму с эффективным радиусом .

Сообщение (видеосигнал) u(t), не содержащее колебаний с частотами выше Fm, так же как и сигнал, может быть представлено вектором в m-мерном пространстве, где m=2TFm. Совокупность возможных сообщений определяет это пространство (пространство сообщений). На рис. 2.11 представлена двухмерная модель этого пространства с двумя различными сообщениями и и2.

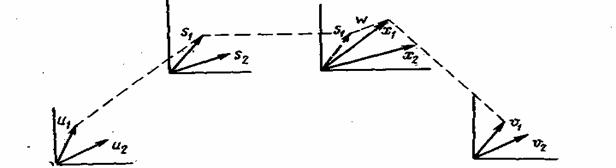
Рис. 2.11 Геометрическая модель системы связи

При передаче сообщение u(t) преобразовывается в сигнал s(t) с использованием некоторого переносчика f(t). Математически эту операцию формирования сигнала можно представить в виде

(2.125)

где М — оператор, в общем случае нелинейный. Геометрически формирование сигнала может быть представлено как преобразование пространства сообщений U в пространство сигналов S: векторы и и2.

преобразуются в векторы s1 и s2.

Мерность пространства сообщений т в общем случае не равна мерности пространства сигналов m. При однополосной передаче m=п. В случае амплитудной модуляции сигналы имеют вдвое большее число координат, чем сообщения: n=2m, а при частотной пространство сигналов имеет значительно большее число измерений, чем пространство сообщений.

При наложении помехи на сигнал создается область неопределенности, в которую попадают принятые сигналы x=s+ω. Взаимодействие сигнала и помехи можно выразить оператором

(2.126)

Оператор Ψ преобразует пространство сигналов S в пространство принятых сигналов X: векторы s1 и s2 переходят в x1 и х2.

Приемник по принятым сигналам х воспроизводит переданное сообщение

(2.127)

т. е. преобразует пространство сигналов X в пространство принятых сообщений V.

Если помеха отсутствует, то принятый сигнал преобразуется в сообщение обратным оператором . В этом случае принятое сообщение тождественно переданному .

При наличии помех сообщения на приеме воспроизводятся с некоторой ошибкой: вместо сообщения может быть воспроизведено сообщение и2наоборот. Ошибка произойдет, когда результирующий вектор х окажется ближе к концу вектора того сигнала s, который в данный момент не передается. Можно построить приемник, воспроизводящий сообщение всякий раз, когда конец вектора х ближе к концу вектора , чем к концу вектора s2 и наоборот. Такой приемник по Котельникову называется идеальным или оптимальным. Очевидно, ошибка при оптимальном приеме будет тем меньше, чем больше расстояние d между соседними сигналами. Это расстояние, в свою очередь, зависит от расстояния r между соседними сообщениями и от вида оператора М, который определяет способ формирования сигнала (в частности, способ модуляции).

2.11. Различимость сигналов

В системах передачи сообщений обычно используется ансамбль сигналов

(2.128)

При двоичной передаче этот ансамбль состоит всего из двух сигналов. В многопозиционной системе число сигналов равно основанию кода т, в многоканальной системе — числу каналов. Передаваемые сигналы, очевидно, должны отличаться друг от друга настолько, чтобы их можно было уверенно различить, а следовательно, разделить на приеме.

Геометрически каждому сигналу (2.128) соответствует вектор в n-мерным пространстве. Мы полагаем здесь, что сигналы имеют одинаковую длительность Т и ограничены полосой частот F. Квадрат расстояния между любой парой сигналов (векторов) согласно (2.124) равен:

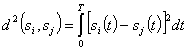(2.129)

Величина расстояния d полностью характеризует различие между сигналами: чем больше d, тем больше это различие. Раскрывая скобки в (2,129), получаем

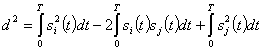
Крайние члены определяют энергию сигналов, а средний член — взаимную корреляцию между сигналами. Для сигналов, имеющих одинаковую энергию

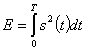
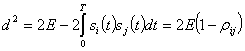(2.130)

где 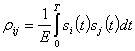(2.131)

— коэффициент взаимной корреляции сигналов.

Итак, различие между сигналами полностью определяется коэффициентом взаимной корреляции между ними. С увеличением различие между сигналами уменьшается и их полное разделение на приеме становится невозможным.

Условием разделения сигналов является выполнение неравенства

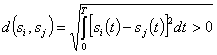(2.132)

откуда

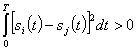
или

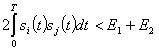(2.133)

В случае сигналов с равными энергиями

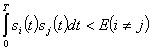(2.134)

или

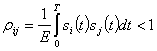(2.135)

Таким образом, для того чтобы можно было разделить сигналы равных энергий, их скалярное произведение (для случайных сигналов — функция взаимной корреляции) должно быть меньше энергии любого из них или коэффициент корреляции при меньше единицы.

Из выражения (2.135) непосредственно следует, что ортогональность сигналов является достаточным условием их разделения. В случае

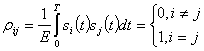
Таким образом, степень различия между сигналами можно характеризовать величиной коэффициента или коэффициента различимости

(2.137)

В системах двух сигналов максимальная различимость будет иметь место при выполнении условия

(2.138)

Сигналы, удовлетворяющие равенству (2.138), называются противоположными. С геометрической точки зрения противоположные сигналы представляются векторами, сдвинутыми друг относительно друга на угол π. Для противоположных сигналов , для ортогональных , для всех других сигналов .

Заметим, что задача разделения сигналов в той или иной форме возникает всегда при передаче сообщений по каналам связи. Эта задача возникает не только при разделении полезных сигналов, но и при выделении полезных сигналов из помех.

Вопросы для повторения

1. Дайте определение детерминированного и случайного процессов. Приведите примеры.

2. Какие сигналы называются простыми и какие сложными? Приведите примеры. Что называется базой сигнала?

3. Какие процессы называются стационарными?

4. Определите среднее значение случайного процесса по времени и среднестатическое значение. Для каких процессов эти значения совпадают?

5. Перечислите основные свойства функции корреляции. Что называется интервалом корреляций?

6. Как описываются статистические свойства дискретных сообщений? Какие процессы называются Марковскими?

7. Какими законами определяются распределения вероятностей мгновенных значении, огибающей и фазы флуктуационной помехи?

8. Что такое "белый шум"? Каковы его свойства?

9. Поясните разложение сигнала в ряде Фурье и в ряд Котельникова как разложение по ортогональным функциям.

10. Поясните связь между функцией корреляции и энергетическим спектром и соответственно связь Между интервалом корреляции и эффективной шириной спектра.

11. Как определяются огибающая и фаза узкополосного процесса на основании понятия «аналитического сигнала»?

12. Какие сигналы называются ортогональными и какие ортогональными «в усиленном смысле»?

13. Как изменяются статические свойства стационарного процесса при прохождении его через линейную Систему?

14. При каких условиях может иметь место нормализация случайного процесса?

15. Дайте геометрическое определение различимости сигналов.