Преобразование дискретного сообщения в сигнал состоит из двух операций: кодирования и модуляции. Кодирование определяет закон построения сигнала, а модуляция — вид формируемого сигнала, который должен передаваться по каналу связи.

Простейшим примером дискретного сообщения является текст. Любой текст состоит из конечного числа элементов: букв, цифр, знаков препинания. Для европейских языков число элементов колеблется от 52 до 55, для восточных языков оно может исчисляться сотнями и даже тысячами. Так как число элементов в дискретном сообщении конечно, то их можно пронумеровать и тем самым свести передачу сообщения к передаче последовательности чисел.

Так, для передачи букв русского алфавита (их 32) необходимо передавать числа от 1 до 32. Для передачи любого числа, записанного в десятичной форме, требуется передача десяти цифр от 0 до 9. Практически для этого нужно передавать по каналу связи десять сигналов, соответствующих различным шифрам. Систему передачи дискретных сообщений можно существенно упростить, если воспользоваться при кодировании двоичной системой счисления.

В десятичной системе основанием счисления является число 10. Поэтому любое число N можно представить в виде

N (1.2)

где ,— коэффициенты, принимающие значения от 0 до 9. Так, число 265 можно записать как . Очевидно, в качестве основания счисления можно принять любое целое число т и представить число N как (1.3)

где коэффициенты, принимающие значение от 0 до m-1.

Задаваясь величиной т, можно построить любую систему счисления. При т=2 .получим двоичную систему, в которой числа записываются при помощи всего лишь двух цифр: 0 и 1. Например, число 13 в двоичной системе записывается 1101, что соответствует выражению . Арифметические действия в двоичной системе весьма простые. Так, сложение осуществляется по следующим правилам: 0+0=0;0+1=1;1+0=1;1+1=10. Различают еще символическое поразрядное сложение без переноса в высший разряд, так называемое «сложение по модулю два». Правила этого сложения следующие: 00=0;01=1;10=1;11=0;

Если преобразовать последовательность элементов сообщения в последовательность двоичных чисел, то для передачи последних по каналу связи достаточно передавать всего лишь два кодовых символа: 0 и 1. Практическая реализация такой передачи весьма простая. Например, символы 0 и 1 могут передаваться колебаниями с различными частотами или посылками постоянного тока равной полярности. Благодаря своей простоте двоичная систему счисления нашла широкое применение при кодировании дискретных сообщений.

При кодировании происходит процесс преобразования элементов сообщения в соответствующие им числа (кодовые символы). Каждому элементу сообщения присваивается определенная совокупность кодовых символов, которая называется кодовой комбинацией. Совокупность кодовых комбинаций, обозначающих дискретные сообщения, называется кодом. Правило кодирования обычно выражается кодовой таблицей, в которой приводятся алфавит кодируемых сообщений и соответствующие им кодовые комбинации (см. табл. l.l и l.2). Множество возможных кодовых символов

Таблица 11 Таблица 12

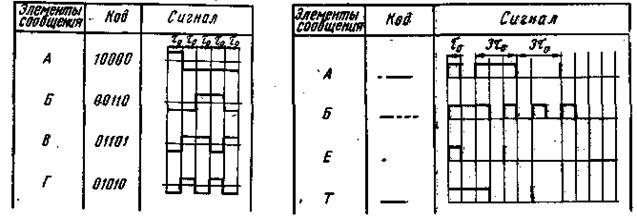
называется кодовым алфавитом, а их количество – основанием кода. В общем случае при основании, когда m правила кодирования N элементов сообщения сходятся к правилам записи N различных чисел в m-ичной системе счисления. Число символов n, образующих кодовую комбинацию, называется значность кода, или длиной кодовой комбинации.

В зависимости от системы счисления, используемой при кодировании, различают двухпозиционные и многопозиционные коды. К первым относятся все коды, в которых используется двоичная система счисления. Часто эти коды называют двоичными. К многопозиционным кодам относятся все коды, в которых число позиций (основание кода) больше двух. Различают коды равномерные и неравномерные.

Равномерными называют такие коды, у которых все кодовые комбинации имеют одинаковую длину. Для равномерного кода число возможных кодовых комбинаций равно т^п. Примером такого кода является пятизначный код Бодо. Этот код содержит пять двоичных элементов (т = 2, n = 5). Число возможных кодовых комбинаций равно 2⁵ = 32, что достаточно для кодирования всех букв алфавита. В табл. 1.1 приведено несколько кодовых комбинаций кода Бодо для случая, когда символ 1 передается положительным импульсом длительности τ, а символ 0 — отрицательным импульсом той же длительности. Время передачи любой кодовой комбинации равно 5τ. Применение равномерных кодов упрощает построение автоматических буквопечатающих устройств и не требует передачи разделительных символов между кодовыми комбинациями.

Неравномерные коды характерны тем, что у них кодовые комбинации отличаются друг от друга не только взаимным расположением символов 0 и 1, но и их количеством. Это приводит к тому, что различные кодовые комбинации имеют разную длительность.

Типичным примером неравномерных кодов является код Морзе, в котором символы 0 и 1 используются только в двух сочетаниях: как одиночные (1 и 0) или как тройные (111 и 000). Сигнал, соответствующий одной единице, называется точкой, трем единицам — тире. Символ 0 используется как знак, отделяющий точку от тире, точку от точки и тире от тире. Совокупность 000 используется как разделительный знак между кодовыми комбинациями. Изложенный принцип построения кода поясняется табл. 1.2, в которой приведено несколько кодовых комбинаций для случая передачи однополярными импульсами. Из таблицы видно, что время передачи различных кодовых комбинаций неодинаково. Самая короткая кодовая комбинация (буква «Е») по длительности равна 4 τ, а самая длинная (цифра 0) —22τ. Средняя длительность кодовой комбинации при передаче твиста на русском языке равна примерно 9,5τ. По сравнению с пятизначным равномерным кодом Бодо это почти в два раза больше.

По помехоустойчивости коды делятся на обыкновенные и корректирующие. Коды, у которых все возможные кодовые комбинации используются для передачи информации, называются обыкновенными или кодами без избыточности. В обыкновенных равномерных кодах превращение одного символа комбинации в другой, например 1 в 0 или 0 в 1, приводит к появлению новой возможной комбинации, т. е. к ошибке.

Корректирующие коды строятся так, что для передачи сообщения используются не все возможные кодовые комбинации, а лишь некоторая их часть. Тем самым создается возможность обнаружить и поправлять ошибки при неправильном воспроизведении некоторого числа символов.

Рис. 1.3. Функциональная схема системы передачи дискретных сообщений

Корректирующие свойства кодов достигаются ценой введения в кодовые комбинации дополнительных (избыточных) символов.

Декодирование состоит в восстановлении сообщения по принимаемым кодовым символам. Устройства, осуществляющие кодирование и декодирование, называются соответственно кодером и декодером. Как правило, это нелинейные логические устройства. На рис. 1.3 изображена функциональная схема системы передачи дискретных сообщений, а на рис. 1.4 и 1.5 поясняются процесс преобразования дискретного сообщения в сигнал и обратно, преобразование принятого сигнала в сообщение.

Рис. 1.4. Процесс преобразования дискретного сообщения в сигнал

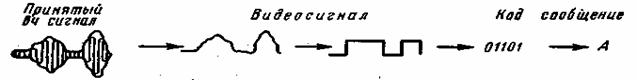
Рис. 1.5. Процесс восстановления переданного сообщения в приемнике

Передача сообщений по каналу связи осуществляется с помощью некоторого физического процесса, который называется переносчиком. В электросвязи таким переносчикам является электрическое колебание.

Всякий сигнал — будь то сигнал телеграфный, телефонный или любой другой — получается путем модуляции. Немодулированный переносчик не несет информации — он подобен чистому листу бумаги, в то время как модулированный переносчик можно сравнить с листом бумаги, на котором написаны буквы, знаки, отображающие ту или иную информацию.

Модуляция состоит в том, что один из параметров переносчика f(a,b,c,…) изменяется во времени в соответствии с передаваемым сообщением u(t), например,

(1.4)

где т =— коэффициент модуляции.

Если изменяется (модулируется) параметр с, то имеем c-модуляцию, если изменяется параметр b, то имеемb-модуляцию и т. д. Модулированные сигналы различаются переносчиками и модулируемыми параметрами. Число возможных видов модуляции при данном виде переносчика определяется числом его параметров.

При передаче сообщений на большие расстояния переносчиком обычно является синусоидальное колебание высокой частоты

f(t)= (1.5)

Параметрами этого колебания являются амплитуда А, частота ω и фаза φ. Каждый из этих параметров можно модулировать и получить соответственно: амплитудную модуляцию (AM), частотную модуляцию (ЧМ) и фазовую модуляцию (ФМ). При этом данный параметр переносчика имеет приращение, пропорциональное u(t). Так,

при AM A= (1.6)

при ФМ (1.7)

при ЧМ (1.8)

Если сообщение закодировано двоичным кодом, то модулируемый параметр будет принимать только два значения: одно будет соответствовать передаче символа 1, другое — передаче символа 0. В этом случае модуляцию называют манипуляцией.

В современных системах связи, особенно в многоканальных, в качестве переносчика часто используется периодическая последовательность импульсов определенной формы. Параметрами такой последовательности являются амплитуда импульсов, длительность, их положение во времени (фаза) и частота следования. Это позволяет получить четыре основных вида импульсной модуляции: амплитудно-импульсную модуляцию (АИМ), широтно-импульсную модуляцию (ШИМ), фазо-импульсную модуляцию (ФИМ) и частотно-импульсную (ЧИМ).

В системах радиосвязи термин «импульсная модуляция», по существу, означает двойную модуляцию: первичную модуляцию последовательности импульсов передаваемым сообщением и вторичную модуляцию высокочастотного синусоидального колебания напряжением, получаемым в результате первичной модуляции. При этом во второй ступени модуляции используются рассмотренные выше способы модуляции синусоидального переносчика (AM, ЧМ, ФМ). В результате получается целый ряд систем с импульсной модуляцией: АИМ- AM, ФИМ-АМ, ШИМ-ЧМ, ШИМ-ФМ и т. д.

В некоторых случаях модулирующее сообщение воздействует одновременно не на один, а на несколько параметров. Такую модуляцию называют смешанной. Возможны, например, амплитудно-частотная, амплитудно-фазовая модуляции и т. п.