11.3.2. ALOHA с выделением временных интервалов
11.3.3. Алгоритм ALOHA с использованием резервирования
11.3.4. Сравнение производительности систем S-ALOHA и R-ALOHA
11.3.1. ALOHA
В 1971 году Гавайский университет разработал и начал использовать систему ALOHA. В данном случае спутник применялся для связи нескольких университетских компьютеров посредством протокола произвольного доступа [3-7]. Принцип работы системы чрезвычайно прост и включает в себя следующие режимы.
1. Режим передачи. Пользователи передают данные в любой момент времени, кодируя свои сообщения с помощью кода обнаружения ошибок.
2. Режим ожидания. После передачи сообщения пользователь ожидает от приемника подтверждения (acknowledgment — АСК) приема данных. Иногда передачи различных пользователей перекрываются во времени, что приводит к возникновению ошибок в каждой передаче. В таком случае сообщения пользователей называют конфликтующими. Ошибки обнаруживаются, после чего пользователи получают отрицательное подтверждение приема (negative acknowledgment — NAK).
3. Режим повторной передачи. После получения сообщения NAK информация передается повторно. Естественно, если пользователи попытаются осуществить повторную передачу непосредственно после возникновения ошибки, конфликтная ситуация может повториться. Поэтому повторная передача производится после случайной задержки.
4. Режим истечения времени ожидания. Если после передачи пользователь в течение определенного времени не получил сообщения АСК или NAK, производится повторная передача.
11.3.1.1. Статистика получения сообщений
Предположим, что для работы некоторой системы необходима определенная средняя частота успешного поступления сообщений (пакетов) λ. Вследствие конфликтных ситуаций некоторые из сообщений не будут получены либо будут отклонены. Следовательно, общую частоту поступления сообщений λt, можно определить как сумму частоты успешного поступления сообщений λ и частоты отклонения λr
(11.16)
Обозначим размер сообщения или пакета через b бит. Тогда средний объем успешно переданных данных, иначе говоря пропускную способность канала, р', можно представить следующим образом.
(11.17)
Также можно определить полный информационный обмен канала, G'.
(11.18) .
Если считать максимальную скорость передачи битов (емкость канала) равной R бит/с, нормированную пропускную способность можно записать следующим образом.
(11-19)
Также можем записать нормированный полный информационный обмен.
(11.20)
Нормированная пропускная способность р выражает пропускную способность как часть (0
р1) емкости канала. Нормированный полный информационный обмен G выражает полный информационный обмен как часть (0 G 
) емкости канала. Следует отметить, что G может иметь значения, превышающие 1.
Время передачи пакета может быть выражено в следующем виде.
(11.21)
Подставляя уравнение (11.21) в (11.19) и (11.20), можем записать следующее.
(11.22)
и
(11.23)
Пользователь может успешно передавать данные, если ни один из пользователей не начал передачу в течение предыдущих τ секунд или не начнет ее в течение следующих т секунд. В противном случае возникнет конфликт. Поэтому для успешной передачи каждого сообщения требуется 2τ секунд.
Статистика получения сообщений независимыми пользователями системы связи часто моделируется пуассоновским процессом. Вероятность поступления К новых сообщений в течение т секунд описывается распределением Пуассона [8].
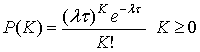(11.24)
где λ — средняя частота поступления сообщений. Поскольку в системе ALOHA пользователи передают данные независимо друг от друга, приведенное выше выражение может быть использовано для вычисления вероятности события, когда в течение временного интервала 2τ будет получено точно К=0 других сообщений. Таким образом, получаем Ps — вероятность успешной (бесконфликтной) передачи пользовательского сообщения. Для вычисления Ps предположим, что информационный обмен описывается распределением Пуассона, после чего подставим в уравнение (11.24) значения λt, и 2τ.
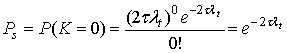(11.25)
В уравнении (11.16) общая частота поступления сообщений λt, определялась как сумма частоты успешного поступления сообщений λ и частоты отклонения данных λr. Тогда, по определению, вероятность успешного получения пакета может быть выражена в следующем виде.
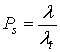(11.26)
Объединяя уравнения (11.25) и (11.26), получаем следующее.
(11.27)
Подставив в формулу (11.27) выражения (11.22) и (11.23), можно записать следующее.
(11.28)
Уравнение (11.28) связывает нормированную пропускную способность 
и нормированный полный информационный обмен G при использовании канала системы ALOHA. График данной зависимости отмечен на рис. 11.20 как "чистый алгоритм ALOHA". По мере роста G увеличивается и до тех пор, пока большое количество конфликтных ситуаций не приведет к снижению пропускной способности. Максимум , равный 1/2е=0,18, достигается при G=0,5. Таким образом, в канале с чистым алгоритмом ALOHA может быть использовано лишь 18% ресурса связи. Простота управления в данном алгоритме достигается за счет снижения емкости канала [7, 9].
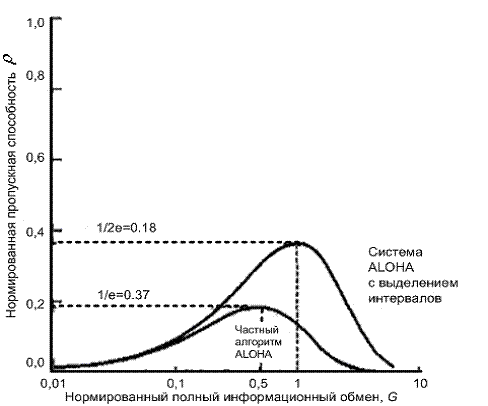
Рис. 11.20. Пропускная способность каналов ALOHA (зависимость доли успешных передач от их общего числа)
11.3.2. ALOHA с выделением временных интервалов
Чистый алгоритм ALOHA можно улучшить, если ввести небольшую координацию между станциями. Примером подобного алгоритма является система ALOHA с выделением временных интервалов (slotted ALOHA — S-ALOHA). Всем станциям посредством метода широковещания передается последовательность синхронизирующих импульсов. Как и в случае чистой системы ALOHA, размер пакетов является постоянным. Сообщения могут передаваться только в течение временного интервала между синхронизирующими импульсами, а начало передачи пакета обязательно должно совпадать с началом интервала. Внесение таких незначительных дополнений в алгоритм ALOHA позволяет вдвое снизить число конфликтных ситуаций, поскольку теперь конфликтовать могут только сообщения, передаваемые в течение одного временного интервала. Можно показать [9, 10], что при использовании алгоритма S-ALOHA сокращение конфликтного промежутка с 2τ до τ дает следующее соотношение между нормированной пропускной способностью и нормированным полным информационным обменом G.
(11.29)
График зависимости (11.29) приведен на рис. 11.20, где он отмечен как "система ALOHA с выделением временных интервалов". В данном случае максимальное значение равно 1/е = 0,37, что в два раза больше аналогичного показателя чистого алгоритма ALOHA.
Режим повторной передачи системы S-ALOHA отличается от соответствующего режима чистого алгоритма тем, что при получении пользователем отрицательного подтверждения (NAK) следующая попытка производится после случайной паузы, длительность которой кратна протяженности временного интервала. Работа алгоритма S-ALOHA представлена на рис. 11.21. После успешной передачи пакета данных пользователь k получает со спутника подтверждение о получении. Также показаны пользователи т и n, которые одновременно начинают передачу пакетов, что приводит к конфликту, и спутник передает сигнал NAK обоим пользователям. Для определения времени повторной передачи обе станции используют генератор случайных чисел. Далее на рисунке показано возможное продолжение: повторная передача пользователями т и п после случайно выбранной паузы. Разумеется, существует вероятность повторения конфликтной ситуации сразу же после конфликта. В этом случае после очередной случайной паузы будет предпринята еще одна попытка повторной передачи.
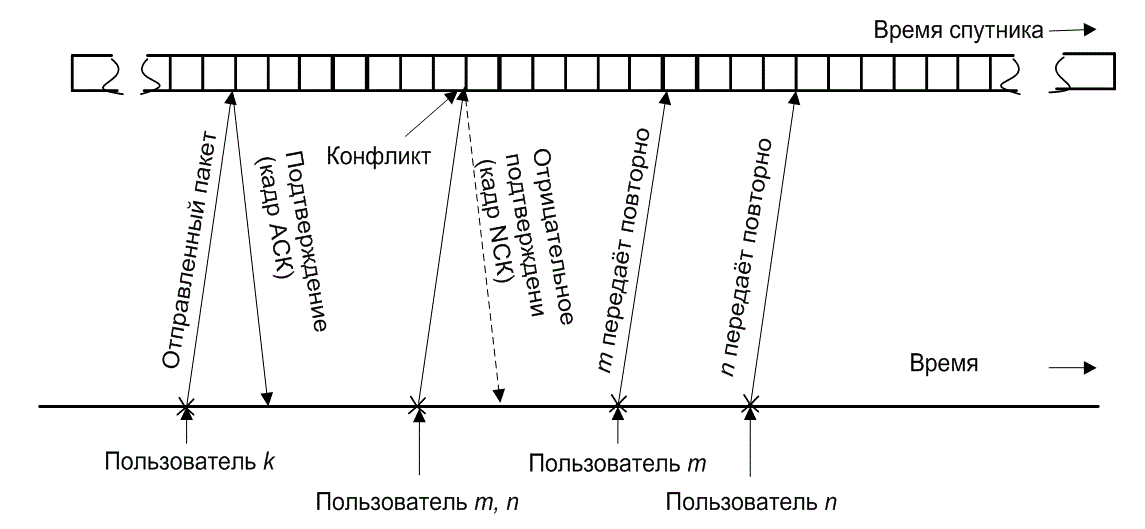
Рис. 11.21. Система произвольного доступа: работа алгоритма ALOHA с выделением временных интервалов.
Пример 11.1. Процесс Пуассона
Пусть передачу и повторную передачу пакетов можно описать как пуассоновский процесс. Определите вероятность возникновения в процессе передачи пакета конфликта с еще одним пользователем (используется алгоритм S-ALOHA). Полная частота передачи пакетов равна λt= 10 пакетов в секунду; длительность пакета τ = 10 мс.
Решение
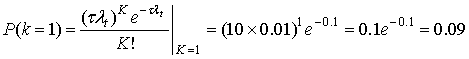
11.3.3. Алгоритм ALOHA с использованием резервирования
Работа систем ALOHA была значительно улучшена в результате введения резервирования (reservation-ALOHA — R-ALOHA) [11]. Системы R-ALOHA могут использоваться в двух основных режимах.
Режим без резервирования (состояние покоя)
1. Выделенный интервал времени разбивается на небольшие подынтервалы резервирования.
2. Эти подынтервалы используются для резервирования интервалов передачи сообщений.
3. После запроса резервирования пользователь ожидает подтверждения и распределения интервалов.
Режим с резервированием
1. Если не выполняется резервирование, временной интервал разбивается на M+ 1 интервалов.
2. Первые М интервалов используются для передачи сообщений.
3. Последний интервал разбивается на подынтервалы, которые используются для резервирования или передачи запросов.
4. Пользователи передают пакеты данных только в выделенных им элементах М интервалов.
Рассмотрим пример использования схемы R-ALOHA, представленный на рис. 11.22. В состоянии покоя время (с целью резервирования) разбивается на небольшие подынтервалы. После резервирования система конфигурируется так, что после М=5 интервалов передачи сообщений следуют V=6 подынтервалов резервирования; далее эта структура повторяется. На рисунке показан процесс отправления запроса и получения подтверждения. В данном примере передающей станции необходимо зарезервировать три интервала времени. В подтверждении спутника содержатся инструкции относительно размещения первого пакета данных. Управление распределено, поэтому все пользователи получают сигнал со спутника и, соответственно, информацию о резервировании и распределении времени. Поэтому в сигнале-подтверждении спутника находится вся необходимая информация, которая заключается в сообщении о выделении первого временного интервала. Как показано на рис. 11.22, в течение следующего интервала времени станция передает второй пакет. Далее пользователь знает, что следующий интервал состоит из шести подынтервалов, предназначенных для резервирования, поэтому передача информационных пакетов в течение этого времени не производится. Третий (последний) пакет отсылается в течение четвертого интервала. Если резервирование не производится, система возвращается в состояние покоя. Поскольку управление выполняется распределенно, все пользователи получают от спутника информацию об изменении состояния системы и соответствующие синхронизирующие импульсы. Другие интересные методы резервирования рассмотрены в [12, 13].
11.3.4. Сравнение производительности систем S-ALOHA и R-ALOHA
В главах 3 и 4 качество схемы цифровой модуляции определялось, в основном, зависимостью РВот Eb/N0. Это особенно полезно, поскольку Eb/N0 является нормированным отношением сигнал/шум. Нормированные кривые позволяют сравнивать производительность различных схем модуляции. Для анализа систем множественного доступа используется подобный показатель — зависимость средней задержки от нормированной пропускной способности. На рис. 11.23 представлена идеальная зависимость задержки от пропускной способности. Для нормированных значений пропускной способности, 0
<1, время задержки равно нулю, при =1 оно неограниченно возрастает. Помимо идеального случая, на рисунке изображена типичная зависимость, а также направление, соответствующее улучшению производительности.
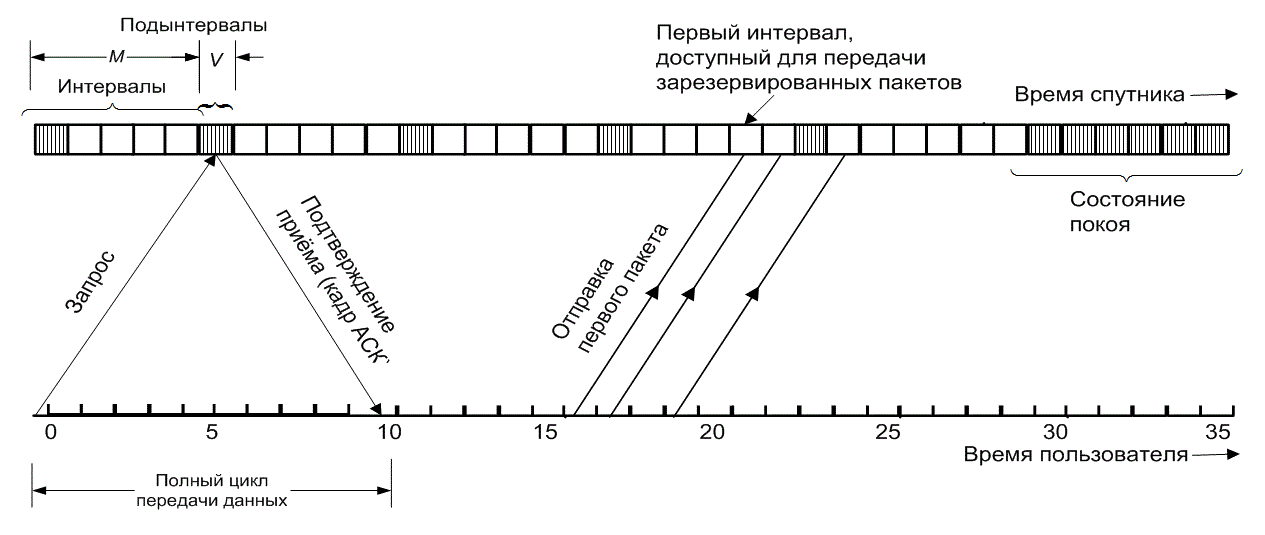
Рис. 11.22. Пример алгоритма ALOHA с использование резервирования. Передающая станция резервирует три интервала (M=5 интервалов, V=6 подынтервалов).
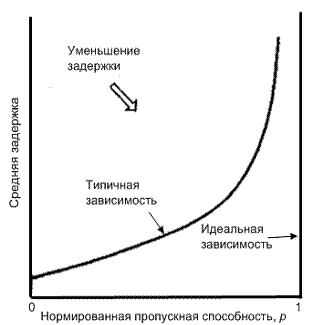
Рис. 11.23. Зависимость времени задержки от пропускной способности
На рис. 11.24 сравниваются зависимости времени задержки от пропускной способности для алгоритмов S-ALOHA и R-ALOHA (формат сообщений: два интервала передачи данных и шесть подынтервалов резервирования). Время задержки этих двух систем сравнивают с помощью идеальной кривой. Для пропускной способности < 0,2 среднее время задержки для системы S-ALOHA меньше, чем для системы R-ALOHA. В то же время для , принадлежащего диапазону 0,2—0,67, R-ALOHA превосходит ALOHA, поскольку у первой среднее время задержки существенно меньше. В чем причина превосходства схемы S-ALOHA при малоинтенсивном обмене данными? Данный алгоритм не требует служебных издержек для резервирования подынтервалов, как в случае R-ALOHA. Таким образом, при небольших значениях производительность R-ALOHA ниже из-за более высоких расходов. При> 0,2 конфликтные ситуации и повторная передача данных в системе S-ALOHA приводят к тому, что время задержки растет быстрее, чем в случае R-ALOHA (и неограниченно возрастает при = 0,37). При более высоких значениях пропускной способности (0,2<<0,67) служебные издержки схемы R-ALOHA полностью окупаются и обеспечивают менее резкое возрастание времени задержки при росте . При использовании схемы R-ALOHA время задержки возрастает до бесконечности при = 0,67.
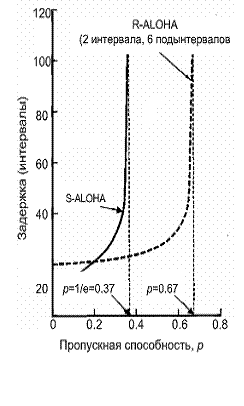Рис. 11.24. Зависимость времени задержки от пропускной способности: спутниковый канал при использовании схем S-ALOHA и R-ALOHA
Пример 11.2. Использование канала связи
а) В качестве меры использования канала выбрана нормированная пропускная способность р. Ее можно найти как отношение успешно переданных данных к полному объему данных (включая отклоненные данные). Найдите нормированную пропускную способность канала связи с максимальной скоростью передачи данных R = 50 Кбит/с, который используется М = 10 станциями связи, каждая из которых передает данные со средней частотой λ = 2 пакета в секунду. Формат системы предусматривает пакеты по b = 1350 бит.
б) Применение какой из описанных систем ALOHA будет оптимальным в данном случае?
Решение
а) Обобщая уравнение (11.19) для информационного потока от нескольких станций, получаем следующее.
б) В данной системе может использоваться только схема R-ALOHA, поскольку два других алгоритма не позволяют использовать 54% ресурса.
11.3.5. Методы опроса
Один из методов упорядочения работы системы произвольного доступа с множественными пользователями состоит во введении контроллера, выявляющего запросы на предоставление услуг путем периодического опроса всех пользователей. Если количество пользователей велико (например, тысячи терминалов), а процесс обмена данными происходит пульсирующим образом, время, выделяемое для опроса всех пользователей, может представлять существенные служебные издержки. Одним из методов быстрого опроса пользователей является поиск по двоичному дереву [4, 14]. На рис. 11.25 представлен пример использования данного метода для реализации "состязания" между пользователями спутниковой связи за обладание ресурсом. Пусть общее число пользователей равно восьми и каждому из них присвоен двоичный код от 000 до 111, как показано на рис. 11.25. Предположим, что терминалы 001, 100 и 110 соревнуются за один канал связи. При поиске по двоичному дереву группа пользователей периодически делится пополам, пока не останется лишь одна ветвь дерева. Терминал, соответствующий этой ветви, и получает право первым использовать канал. Затем операция повторяется, и доступ получает следующий "победитель". Алгоритм поиска состоит из следующих этапов (рис. 11.25).
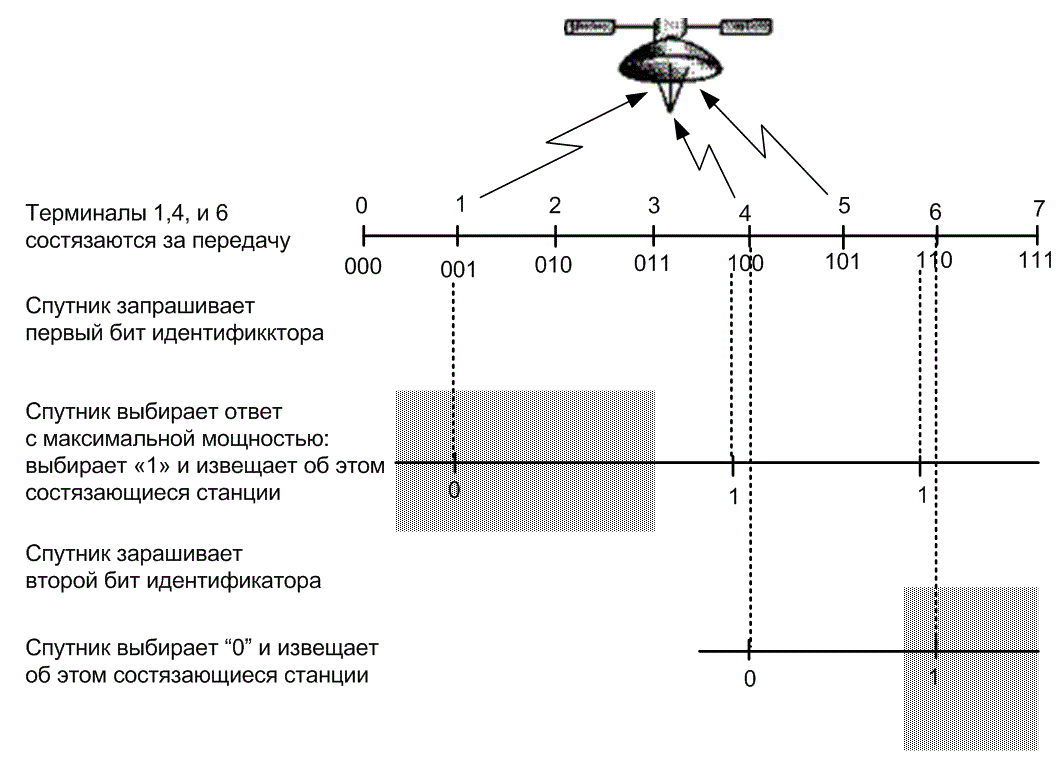
Рис.11.25. Разрешение соастязания между пользователями: поиск по двоичному дереву
1. Спутник запрашивает у состязающихся терминалов первую цифру их двоичных идентификаторов.
2. Терминал 001 передает "0", терминалы 100 и 110, соответственно, "1". Спутник, на основе мощности принятых сигналов, выбирает нуль или единицу. В данном примере была выбрана единица, и об этом были проинформированы пользователи. В настоящий момент половина пользователей прекращает состязание. В данном примере выбывает терминал 001.
3. Спутник запрашивает у оставшихся терминалов вторую цифру идентификационного номера.
4. Терминал 100 передает "0", терминал 110 — "1".
5. Предположим, что спутник выбрал нуль и уведомил об этом пользователей. Терминал 110 выбывает из состязания. Процесс продолжается до тех пор, пока терминал 100 не получит доступ к спутнику.
6. После того как канал связи освобождается, этапы 1-5 повторяются.
Пример 11.3. Сравнение поиска по двоичному дереву и непосредственного опроса
а) Поиск по двоичному дереву требует принятия и = log2Q решений при каждом опросе группы из Q терминалов. Экономия времени возможна в том случае, когда группа является достаточно большой, а среднее количество запросов на услугу невелико. Вычислите время, необходимое для непосредственного опроса группы из 4096 терминалов, с целью предоставления канала связи 100 терминалам. Сравните результат со временем, необходимым для выполнения 100 операций поиска по двоичному дереву для той же группы пользователей. Время, необходимое для опроса одного терминала, и время принятия решения при поиске по двоичному дереву одинаковы и равны 1 с.
б) Выведите уравнение для максимального количества терминалов Q' при котором время непосредственного опроса равно (или меньше) времени поиска по двоичному дереву.
в) Вычислите Q 'для п. а.
Решение
а) Время прямого опроса 4 096 терминалов равно следующему.
Поиск по двоичному дереву для 100 терминалов требует 100 проходов по дереву.
б) Q' является максимальным числом терминалов, при котором в условиях п. а 
. Это происходит в следующем случае.
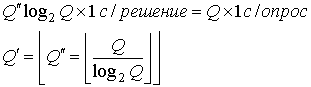(11.30)
Здесь 
bd — наибольшее целое число, не превышающее х.
в) Q 'для п. а равно следующему.
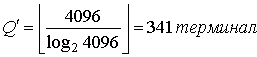
Поиск по двоичному дереву для 341 терминала требует 4 092 с.