На рис. 3 показана условно собственная энтропия H(x) и H(y), условные энтропии H(x/y) иH(y/x) и совместная энтропия H(x, y). Из этого рисунка, в частности, следуют соотношения (17) и (18).
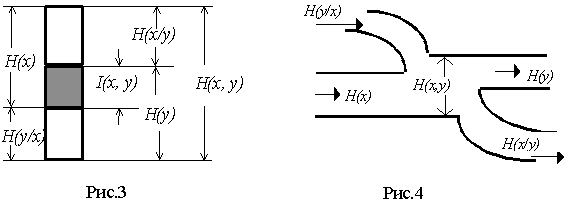
![]() Часть рисунка, отмеченная штриховкой, называется взаимной информацией I(x, y). Она показывает, какое (в среднем) количество информации содержит сообщение x о сообщении y (или наоборот, сообщение y о сообщении x).
Часть рисунка, отмеченная штриховкой, называется взаимной информацией I(x, y). Она показывает, какое (в среднем) количество информации содержит сообщение x о сообщении y (или наоборот, сообщение y о сообщении x).
Как следует из рис. 3,
![]() . (20)
. (20)
Если сообщение x и y полностью независимы, то взаимная информация отсутствует и I(x, y)=0.
Если x и y полностью зависимы ( x и y - содержат одну и ту же информацию), то I(x, y)=H(x)=H(y).
Понятие взаимной информации очень широко используется в теории передачи информации. Требования к взаимной информации различны в зависимости от того, с какой информацией мы имеем дело. Например, если x и y - это сообщения, публикуемые различными газетами, то для получения возможно большей суммарной (совместной) информации взаимная (т.е. одинаковая в данном случае) информация должна быть минимальной. Если же x и y - это сообщения на входе и на выходе канала связи с помехами, то для получения возможно большей информации её получателем необходимо, чтобы взаимная информация была наибольшей. Тогда условная энтропия H(x/y) - это потери информации в канале связи (ненадежность канала), H(y/x) - это информация о помехах(энтропия источника помех - H(n)) , поступающая в канал извне или создаваемая внутренними помехами в канале (схематически этот процесс показан на рис.4).
Вопросы
- Что такое взаимная информация двух источников ( или двух сообщений), чему она равна?
- Что такое ненадежность канала передачи информации, как ее определить через условные вероятности?
- Как определить информацию о помехах в канале передачи информации, используя условные вероятности перехода p(yj/xi)?

