Особое место при анализе процессов, протекающих в радиотехнических и информационных системах, занимает нормальный случайный процесс с нулевым математическим ожиданием и автокорреляционной функцией:

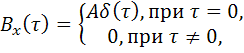(5.78)

где – дельта функция.

Такой случайный процесс получил название «белого шума». Значения «белого шума» при сколь угодно малом значении некоррелированы. При этом, как следует из (5.78)

,

т.е. средняя мощность белого шума неограниченна.

«Белый шум» является математической абстракцией, которая, тем не менее, существенно упрощает анализ процессов в радиотехнических системах. В природе процессов вида «белого шума» не существует, но при определенных предположениях реальные помехи можно описать моделью «белого шума».

Найдем значение коэффициента в (5.78). Для этого подставим (5.78) в (5.68).

.

Используя фильтрующее свойство дельта-функции при , получим

. (5.79)

Отсюда следует, что «белый шум» имеет равномерный энергетический спектр в диапазоне частот от 0 до ∞ со спектральной плотностью мощности . Выражая через из (5.79) и подставляя его в (5.78), получим

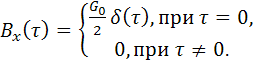(5.80)

Аналогичными рассуждениями при использовании выражения (5.69) можно получить

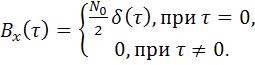(5.81)

Выражение (5.81) наиболее часто используется при решении различных задач радиотехники. Свое название «белый шум» получил по аналогии со световым потоком, отраженным от листа белой бумаги. Такой поток имеет равномерный спектр в очень широком диапазоне частот.

Ввиду того, что автокорреляционная функция «белого шума» представляет собой дельта-функцию, «белый шум» часто называют дельта-коррелированным случайным процессом. Отсутствие корреляции между любыми, сколь угодно близкими значениями «белого шума» означает бесконечно большую скорость изменения процесса.

В радиотехнических задачах моделью «белого шума», в частности описываются тепловые и дробовые шумы элементов радиотехнических устройств.

Тепловые шумы резисторов возникают из-за хаотического теплового движения заряда в проводящих элементах. Внутри объема резистора возникают электромагнитные поля и на внешних зажимах появляется шумовая разность потенциалов. Энергетический спектр шума оказывается очень широким из-за высокой скорости теплового движения электронов и описывается выражением

, (5.82)

где – постоянная Больцмана,

– абсолютная температура (в градусах по Кельвину),

– значение сопротивления резистора.

Из (5.82) следует, что снизить интенсивность теплового шума можно уменьшая . Вот почему в радиолокации, радиоастрономии и космической связи применяют глубокое охлаждение входных цепей радиоприемных устройств.

Дробовой шум возникает в электронных приборах (лампах, транзисторах и т.д.). Природу дробового шума можно пояснить на примере вакуумного диода, в котором электроны эмитируются из катода и затем перемещаются к аноду под действием электрического поля. Ток, создаваемый потоком электронов, представляет собой сумму коротких импульсов тока, обусловленных перемещением электронов от катода к аноду. Хотя время пролета электрона от катода к аноду составляет величину порядка , за счет случайности моментов вылета электронов с поверхности катода суммарный ток носит случайный характер. Энергетический спектр дробового шума также является равномерным в очень широком диапазоне частот за счет малой длительности каждого из импульсов, образующих дробовой шум. Для оценки энергетического спектра дробового шума используется выражение

, (5.83)

где – средние значение тока,

– среднее число электронов, достигающих анода за единицу времени,

– электрический заряд, переносимый каждым электроном.

Соотношение (5.83) получило название формулы Шоттки.