6.2. Обобщенная модель и категории дискретных сигналов
6.3. Корреляционные функции АФМ сигналов
6.4. Вычисление корреляционных функций кодовых последовательностей
6.1. Широкополосная модуляция
К настоящему моменту стало понятно, что для превращения сигнала в широкополосный необходимо соответствующее управление его комплексной огибающей ![]() , т.е. модуляцией мгновенной амплитуды
, т.е. модуляцией мгновенной амплитуды ![]() и мгновенной начальной фазы
и мгновенной начальной фазы ![]() . Как уже отмечалось ранее, «чистая» амплитудная модуляция не является эффективным инструментом обеспечения широкополосности, поскольку она расширяет спектр лишь ценой концентрации энергии сигнала в коротких временных интервалах, что неизбежно приводит к увеличению пиковой мощности.
. Как уже отмечалось ранее, «чистая» амплитудная модуляция не является эффективным инструментом обеспечения широкополосности, поскольку она расширяет спектр лишь ценой концентрации энергии сигнала в коротких временных интервалах, что неизбежно приводит к увеличению пиковой мощности.
В зависимости от характера используемой модуляции все широкополосные сигналы можно разделить на непрерывные и дискретные. Для первых закон модуляции, т.е. комплексная огибающая ![]() , – непрерывная функция времени, тогда как модулируемые параметры вторых (амплитуда, частота, начальная фаза) – кусочно-постоянны, скачкообразно изменяя свои значения только в дискретные моменты времени. Пример непрерывного широкополосного сигнала будет кратко рассмотрен в начале следующей темы, однако в дальнейшем основное внимание будет фокусироваться на дискретных сигналах в силу их доминирующего распространения в большинстве современных и перспективных коммерческих широкополосных систем.
, – непрерывная функция времени, тогда как модулируемые параметры вторых (амплитуда, частота, начальная фаза) – кусочно-постоянны, скачкообразно изменяя свои значения только в дискретные моменты времени. Пример непрерывного широкополосного сигнала будет кратко рассмотрен в начале следующей темы, однако в дальнейшем основное внимание будет фокусироваться на дискретных сигналах в силу их доминирующего распространения в большинстве современных и перспективных коммерческих широкополосных систем.
6.2. Обобщенная модель и категории дискретных сигналов
Версия дискретного сигнала, которая наиболее типична для современных широкополосных систем, может быть описана следующим образом: дискретный сигнал есть последовательность элементарных символов (импульсов) фиксированной формы, повторяющихся с некоторым фиксированным временным интервалом. Упомянутый элементарный импульс, именуемый далее чипом, исчерпывающе характеризуется комплексной огибающей ![]() , задающей его форму и закон внутренней угловой модуляции, если последняя присутствует. Традиционно (но не обязательно), временной интервал
, задающей его форму и закон внутренней угловой модуляции, если последняя присутствует. Традиционно (но не обязательно), временной интервал ![]() между последовательными чипами равен или больше длительности чипа
между последовательными чипами равен или больше длительности чипа ![]() . Модуляция всего сигнала сводится к манипулированию амплитудами, фазами и, возможно, частотами отдельных чипов. В соответствии с этим словесным описанием формальное представление комплексной огибающей дискретного сигнала дается равенством
. Модуляция всего сигнала сводится к манипулированию амплитудами, фазами и, возможно, частотами отдельных чипов. В соответствии с этим словесным описанием формальное представление комплексной огибающей дискретного сигнала дается равенством
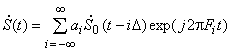 ,
,
где в дополнение к уже расшифрованным обозначениям ![]() и
и ![]() – соответственно комплексная амплитуда и частота (измеряемая сдвигом относительно фиксированной центральной частоты)
– соответственно комплексная амплитуда и частота (измеряемая сдвигом относительно фиксированной центральной частоты) ![]() -го чипа. Очевидно, что последовательность
-го чипа. Очевидно, что последовательность ![]() определяет действительные амплитуды чипов, т.е. их амплитудную модуляцию. Аналогично, последовательности
определяет действительные амплитуды чипов, т.е. их амплитудную модуляцию. Аналогично, последовательности ![]() и
и ![]() задают законы модуляции чипов по фазе и частоте. Рисунок слева иллюстрирует смысл некоторых введенных обозначений.
задают законы модуляции чипов по фазе и частоте. Рисунок слева иллюстрирует смысл некоторых введенных обозначений.
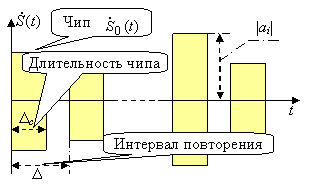
В рамках описанной общей модели можно выделить несколько категорий дискретных сигналов в зависимости от конкретных деталей модуляции чипов.
1. Если манипулируются лишь комплексные амплитуды чипов, а их частоты одинаковы ![]() , сигнал называется амплитудно-фазоманипулированным (АФМ). Традиционное название последовательности комплексных амплитуд чипов
, сигнал называется амплитудно-фазоманипулированным (АФМ). Традиционное название последовательности комплексных амплитуд чипов ![]() – кодовая последовательность или просто код.
– кодовая последовательность или просто код.
2. Если манипуляции подлежат только фазы чипов АФМ сигнала, а их амплитуды неизменны ![]() , АФМ сигнал именуют фазоманипулированным (ФМ). ФМ сигналы характерны для так называемых широкополосных систем с прямым расширением спектра (см. раздел 11.1).
, АФМ сигнал именуют фазоманипулированным (ФМ). ФМ сигналы характерны для так называемых широкополосных систем с прямым расширением спектра (см. раздел 11.1).
3. Среди ФМ сигналов возможна дальнейшая классификация в зависимости от модуляционного алфавита. В случае бинарных комплексных амплитуд с алфавитом ![]() (или эквивалентно
(или эквивалентно![]() сигнал является бинарным ФМ (БФМ). Квадратурный ФМ алфавит
сигнал является бинарным ФМ (БФМ). Квадратурный ФМ алфавит ![]() , (или эквивалентно
, (или эквивалентно ![]() ) порождает сигнал с квадратурной ФМ (КФМ или ФМ-4). Если же ФМ алфавит принадлежит множеству
) порождает сигнал с квадратурной ФМ (КФМ или ФМ-4). Если же ФМ алфавит принадлежит множеству ![]() (или эквивалентно
(или эквивалентно ![]() ), то получаем
), то получаем ![]() –фазные (ФМ-М) сигналы.
–фазные (ФМ-М) сигналы.
4. Если управлению подвергаются только частоты чипов, а комплексные амплитуды неизменны, сигнал является частотно-манипулированным (ЧМ). Кодовая последовательность подобного сигнала представляет собой последовательность частот ![]() . Сигналы этого типа используются, в частности, в системах с прыгающей частотой (см. раздел 11.1).
. Сигналы этого типа используются, в частности, в системах с прыгающей частотой (см. раздел 11.1).
Возможна и классификация дискретных сигналов, учитывающая его конечность или периодичность:
1. Импульсный или апериодический сигнал содержит конечное число N чипов, т.е. является пакетом из ![]() манипулированных импульсов:
манипулированных импульсов:
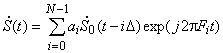 ,
,
что следует из обобщенной модели дискретного сигнала в предположении неравенства нулю действительных амплитуд ![]() только для
только для ![]() , тогда как при
, тогда как при ![]() и
и ![]()
![]() . Длительность апериодического сигнала
. Длительность апериодического сигнала ![]() .
.
2. Периодический сигнал характеризуется повторяющимся законом модуляции с периодом в ![]() чипов:
чипов: ![]() ,
, ![]() . Период последнего в единицах реального времени
. Период последнего в единицах реального времени ![]() , и любой такой сигнал получается, очевидно, повторением с периодом
, и любой такой сигнал получается, очевидно, повторением с периодом ![]() апериодического, являющегося, в свою очередь, однопериодным сегментом периодического сигнала.
апериодического, являющегося, в свою очередь, однопериодным сегментом периодического сигнала.
В обоих случаях параметр ![]() будем называть длиной дискретного сигнала (кода).
будем называть длиной дискретного сигнала (кода).
6.3. Корреляционные функции АФМ сигналов
Корреляционные функции, характеризующие схожесть сдвинутых во времени копий сигналов, критически важны в задачах измерения времени и разрешения. Искусство дизайна широкополосных систем, как это демонстрируется далее, во многих аспектах подразумевает умение находить сигналы с должными корреляционными свойствами. Цель настоящего раздела состоит в получении обобщающего выражения для корреляционных функций АФМ сигналов.
Вне зависимости от того является ли дискретный сигнал финитным или периодическим для вычисления его автокорреляционной функции (АКФ) достаточен интервал ![]() . Подстановка обобщенной модели АФМ дискретного сигнала в выражение, определяющее АКФ, приводит к следующему соотношению
. Подстановка обобщенной модели АФМ дискретного сигнала в выражение, определяющее АКФ, приводит к следующему соотношению
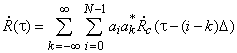 ,
,
в котором
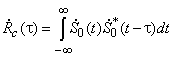
АКФ одного чипа. Замена индекса суммирования ![]() на
на ![]() представляет последний результат как
представляет последний результат как
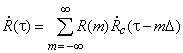 ,
,
где
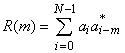
– АКФ кодовой последовательности ![]() , характеризующая схожесть последней со своей копией, сдвинутой на
, характеризующая схожесть последней со своей копией, сдвинутой на ![]() позиций.
позиций.
Сравнение выражения для АКФ АФМ сигнала с его моделью позволяет заключить, что АКФ АФМ сигнала может сама интерпретироваться как АФМ сигнал! При этом чипом последнего служит АКФ ![]() исходного чипа, тогда как кодовой последовательностью оказывается АКФ
исходного чипа, тогда как кодовой последовательностью оказывается АКФ ![]() кодовой последовательности
кодовой последовательности ![]() исходного сигнала. Следовательно, при заданном чипе
исходного сигнала. Следовательно, при заданном чипе ![]() АКФ АФМ сигнала полностью определяется АКФ
АКФ АФМ сигнала полностью определяется АКФ ![]() кодовой последовательности (в дальнейшем АКФ кода), и синтез АФМ сигналов с хорошими корреляционными свойствами состоит в отыскании последовательностей с хорошими АКФ.
кодовой последовательности (в дальнейшем АКФ кода), и синтез АФМ сигналов с хорошими корреляционными свойствами состоит в отыскании последовательностей с хорошими АКФ.
Для построения многопользовательских CDMA систем требуются семейства дискретных сигналов с приемлемыми взаимными корреляционными свойствами. Если синхронизация всех сигнатур (асинхронный вариант CDMA) невозможна, то неизбежно возникают помехи множественного доступа (ПМД), уровень которых определяется взаимной корреляционной функцией (ВКФ) между ![]() –й и
–й и ![]() –й сигнатурами:
–й сигнатурами:
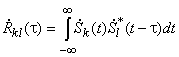
свидетельствующей о подобий ![]() –й и
–й и ![]() –й сигнатур, сдвинутых во времени на
–й сигнатур, сдвинутых во времени на ![]() . Повторяя проделанные при определении АКФ АФМ сигналов выкладки, снова приходим к заключению, что при заданном чипе
. Повторяя проделанные при определении АКФ АФМ сигналов выкладки, снова приходим к заключению, что при заданном чипе ![]() свойства ВКФ АФМ сигналов полностью определяются ВКФ кодов
свойства ВКФ АФМ сигналов полностью определяются ВКФ кодов ![]()
![]() –й и
–й и ![]() –й сигнатур (при
–й сигнатур (при ![]() ВКФ становится АКФ):
ВКФ становится АКФ):
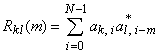 ,
,
характеризующей степень сходства k-й последовательности со сдвинутой на ![]() позиций репликой l-го кода.
позиций репликой l-го кода.
6.4. Вычисление корреляционных функций кодовых последовательностей
Рассмотрим кодовую последовательность ![]() . Если она используется для формирования импульсного сигнала, то в общей модели АФМ сигнала
. Если она используется для формирования импульсного сигнала, то в общей модели АФМ сигнала ![]() для всех отрицательных
для всех отрицательных ![]() и
и ![]() , так что апериодическая или импульсная АКФ
, так что апериодическая или импульсная АКФ ![]() кода
кода ![]() вычисляется как
вычисляется как
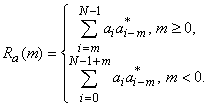 .
.
Очевидно, что апериодическая АКФ представляет собой скалярное произведение вектора ![]() с собственной копией, нециклически сдвинутой на
с собственной копией, нециклически сдвинутой на ![]() позиций. Последнее означает, что при сдвиге вектора
позиций. Последнее означает, что при сдвиге вектора ![]() вправо
вправо ![]() или влево
или влево ![]() сумма в
сумма в ![]() учитывает только перекрывающиеся компоненты
учитывает только перекрывающиеся компоненты ![]() и его сдвинутой копии, а все остальные полагаются равными нулю. Например, для вычисления
и его сдвинутой копии, а все остальные полагаются равными нулю. Например, для вычисления ![]() первоначально следует записать одну под другой исходную последовательность и ее комплексно сопряженную копию, сдвинутую вправо на одну позицию, а затем выполнить поэлементное перемножение и просуммировать полученные произведения:
первоначально следует записать одну под другой исходную последовательность и ее комплексно сопряженную копию, сдвинутую вправо на одну позицию, а затем выполнить поэлементное перемножение и просуммировать полученные произведения:
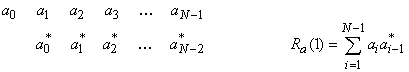 .
.
Обратимся теперь к периодическому сигналу, т.е. положим ![]() . Тогда в выражении для АКФ сумма всегда содержит
. Тогда в выражении для АКФ сумма всегда содержит ![]() слагаемых, поскольку
слагаемых, поскольку ![]() и т.д., периодическая АКФ
и т.д., периодическая АКФ ![]() вычисляется как
вычисляется как
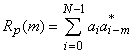 ,
,
причем индекс суммирования ![]() вычисляется по
вычисляется по ![]() .
.
В этом случае скалярное произведение вычисляется для исходной кодовой последовательности и ее циклически сдвинутой копии, где при ![]()
![]() крайних левых «пустых» позиций заполняются символами, «вытолкнутыми» вправо. Например, схема вычисления
крайних левых «пустых» позиций заполняются символами, «вытолкнутыми» вправо. Например, схема вычисления ![]() выглядит следующим образом:
выглядит следующим образом:
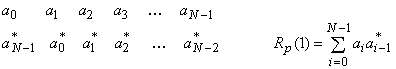 .
.
Из вышеприведенных определений непосредственно вытекает связь между периодической и апериодической АКФ
![]()
Отметим, что нормированные версии апериодической и периодической АКФ определяются как
![]() ,
,
где
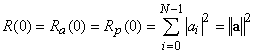 .
.
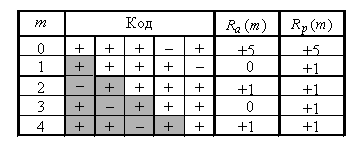
Пример 6.4.1. Приведенная слева таблица иллюстрирует вычисление апериодической ![]() и периодической
и периодической ![]() АКФ бинарной последовательности длины
АКФ бинарной последовательности длины ![]()
![]() . Здесь, как это обычно принято, символы бинарного алфавита +1 и –1 представлены знаками + и – соответственно. Два последних столбца таблицы содержат значения ненормированной АКФ, а затененные клетки отвечают символам, не участвующим в вычислении апериодической АКФ. Нормированные АКФ получаются в результате деления всех полученных значений АКФ на
. Здесь, как это обычно принято, символы бинарного алфавита +1 и –1 представлены знаками + и – соответственно. Два последних столбца таблицы содержат значения ненормированной АКФ, а затененные клетки отвечают символам, не участвующим в вычислении апериодической АКФ. Нормированные АКФ получаются в результате деления всех полученных значений АКФ на ![]() . Непосредственная проверка подтверждает связь между апериодической и периодической АКФ:
. Непосредственная проверка подтверждает связь между апериодической и периодической АКФ: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
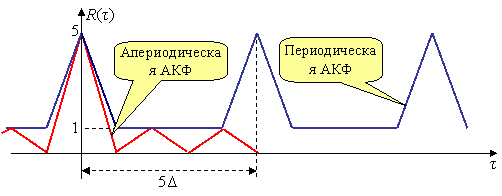
На рисунке построены ненормированные АКФ БФМ видеосигнала с прямоугольными чипами длительности ![]() , модулированными рассматриваемой кодовой последовательностью.
, модулированными рассматриваемой кодовой последовательностью.
Говоря о взаимной корреляции двух последовательностей одной длины, можно вновь различать апериодическую ![]() и периодическую
и периодическую ![]() ВКФ, определяемые как
ВКФ, определяемые как
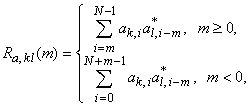 и
и 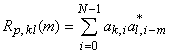 .
.
Для ВКФ остается в силе и соотношение устанавливающее связь между периодической и апериодической версиями:
![]() .
.
6.5. Корреляционные функции ЧМ сигналов
Решим теперь ту же задачу, но в приложении к ЧМ сигналам. Комплексную огибающую ЧМ сигнала можно записать как
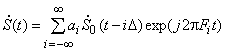 .
.
Тогда, интересуясь только значениями АКФ ЧМ сигналов при задержках, кратных длительности чипа: ![]() , где
, где ![]() – целое, после аналогично выполненных выше преобразований получаем
– целое, после аналогично выполненных выше преобразований получаем
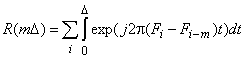 .
.
Типичным для ЧМ является использование равномерного частотного алфавита, в котором ![]() , где шаг по частоте
, где шаг по частоте ![]() не меньше полосы, занимаемой чипом. Таким образом, спектры двух чипов с частотами
не меньше полосы, занимаемой чипом. Таким образом, спектры двух чипов с частотами ![]() и
и ![]() , не перекрываются, а сами чипы ортогональны независимо от их временного рассогласования всякий раз, как
, не перекрываются, а сами чипы ортогональны независимо от их временного рассогласования всякий раз, как ![]() . Учитывая последнее, интеграл отличен от нуля только для тех значений
. Учитывая последнее, интеграл отличен от нуля только для тех значений ![]() , при которых частоты
, при которых частоты ![]() и
и ![]() совпадают, а значение АКФ аккумулирует число совпадений частот в последовательности
совпадают, а значение АКФ аккумулирует число совпадений частот в последовательности ![]() и его копии
и его копии ![]() , сдвинутой на
, сдвинутой на ![]() чипов.
чипов.
Пример 6.5.1. Пусть ЧМ сигнал описывается последовательностью частот вида ![]() , где все значения определены в числе
, где все значения определены в числе ![]() . Тогда для вычисления ее апериодической и периодической АКФ следует записать одну по другой данную последовательность и все ее сдвинутые копии, а затем осуществить подсчет числа совпадений между исходной последовательностью и ее копии, сдвинутой на m позиций.
. Тогда для вычисления ее апериодической и периодической АКФ следует записать одну по другой данную последовательность и все ее сдвинутые копии, а затем осуществить подсчет числа совпадений между исходной последовательностью и ее копии, сдвинутой на m позиций.
6.6. Выигрыш от обработки
В заключении главы осуществим оценку выигрыша от обработки, присущего дискретным сигналам. Для АФМ сигналов полоса оценивается величиной ![]() , а длительность сигнала составляет
, а длительность сигнала составляет ![]() , так что выигрыш от обработки составит
, так что выигрыш от обработки составит ![]() , т.е. в точности совпадает с длиной кодовой последовательности. Для ЧМ сигналов с
, т.е. в точности совпадает с длиной кодовой последовательности. Для ЧМ сигналов с ![]() различными номиналами разнос между соседними частотами, как правило, выбирается порядка
различными номиналами разнос между соседними частотами, как правило, выбирается порядка ![]() с тем, чтобы минимизировать общую полосу, занимаемую сигналом
с тем, чтобы минимизировать общую полосу, занимаемую сигналом ![]() , при длительности равной
, при длительности равной ![]() . В результате выигрыш от обработки составляет
. В результате выигрыш от обработки составляет ![]() , т.е. равен произведению длины (в числе чипов последовательности)
, т.е. равен произведению длины (в числе чипов последовательности) ![]() на число различных частот
на число различных частот ![]() .
.

