Спектральная плотность (spectral density) характеристик сигнала - это распределение энергии или мощности сигнала по диапазону частот. Особую важность это понятие приобретает при рассмотрении фильтрации в системах связи. Мы должны иметь возможность оценить сигнал и шум на выходе фильтра. При проведении подобной оценки используется спектральная плотность энергии (energy spectral density - ESD) или спектральная плотность мощности (power spectral density - PSD).
1.3.1. Спектральная плотность энергии
Общая энергия действительного энергетического сигнала 
, определенного в интервале 
описывается уравнением (1.7). Используя теорему Парсеваля [1], мы можем связать энергию такого сигнала, выраженную во временной области, с энергией, выраженной в частотной области:
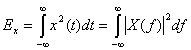, (1.13)
где 
- Фурье-образ непериодического сигнала . (Краткие сведения об анализе Фурье можно найти в приложении А.) Обозначим через 
прямоугольный амплитудный спектр, определенный как
(1.14)
Величина является спектральной плотностью энергии (ESD) сигнала . Следовательно, из уравнения (1.13) можно выразить общую энергию путем интегрирования спектральной плотности по частоте.
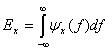(1.15)
Данное уравнение показывает, что энергия сигнала равна площади под на графике в частотной области. Спектральная плотность энергии описывает энергию сигнала на единицу ширины полосы и измеряется в Дж/Гц. Положительные и отрицательные частотные компоненты дают равные энергетические вклады, поэтому, для реального сигнала , величина 
представляет собой четную функцию частоты. Следовательно, спектральная плотность энергии симметрична по частоте относительно начала координат, а общую энергию сигнала можно выразить следующим образом.
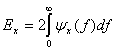(1.16)
1.3.2. Спектральная плотность мощности
Средняя мощность 
действительного сигнала в периодическом представлении определяется уравнением (1.8). Если - это периодический сигнал с периодом 
, он классифицируется как сигнал в периодическом представлении. Выражение для средней мощности периодического сигнала дается формулой (1.6), где среднее по времени берется за один период .
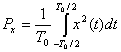(1.17,а)
Теорема Парсеваля для действительного периодического сигнала [1] имеет вид
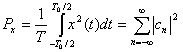, (1.17,б)
где члены 
являются комплексными коэффициентами ряда Фурье для периодического сигнала (см. приложение А).
Чтобы использовать уравнение (1.17,6), необходимо знать только значение коэффициентов . Спектральная плотность мощности (PSD) 
периодического сигнала , которая является действительной, четной и неотрицательной функцией частоты и дает распределение мощности сигнала по диапазону частот, определяется следующим образом.
(1.18)
Уравнение (1.18) определяет спектральную плотность мощности периодического сигнала как последовательность взвешенных дельта-функций. Следовательно, PSD периодического сигнала является дискретной функцией частоты. Используя PSD, определенную в уравнении (1.18), можно записать среднюю нормированную мощность действительного сигнала.
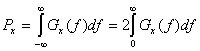(1.19)
Уравнение (1.18) описывает PSD только периодических сигналов. Если - непериодический сигнал, он не может быть выражен через ряд Фурье; если он является непериодическим сигналом в периодическом представлении (имеющим бесконечную энергию), он может не иметь Фурье-образа. Впрочем, мы по-прежнему можем выразить спектральную плотность мощности таких сигналов в пределе. Если сформировать усеченную версию 
непериодического сигнала в периодическом представлении , взяв для этого только его значения из интервала (
), то будет иметь конечную энергию и соответствующий Фурье-образ 
. Можно показать [2], что спектральная плотность мощности непериодического сигнала определяется как предел.
(1.20)
Пример 1.1. Средняя нормированная мощность
а) Найдите среднюю нормированную мощность сигнала 
, используя усреднение по времени.
б) Выполните п. а путем суммирования спектральных коэффициентов.
Решение
а) Используя уравнение (1.17,а), имеем следующее.
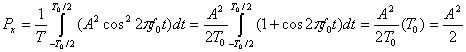
б) Используя уравнения (1.18) и (1.19), получаем следующее.
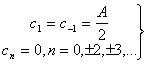(см. приложение А)
