4.1. Классификация и характеристики параметрических цепей
Параметрическими называются радиотехнические цепи, оператор преобразования которых зависит от времени. Закон преобразования сигнала в параметрической цепи записывается выражением:
![]() , (4.1)
, (4.1)
где ![]() – оператор преобразования, зависящий от времени, причем эта зависимость в большинстве случаев носит принудительный характер. Если при этом выполняется условие
– оператор преобразования, зависящий от времени, причем эта зависимость в большинстве случаев носит принудительный характер. Если при этом выполняется условие
![]() , (4.2)
, (4.2)
то такие цепи являются линейными параметрическими цепями.
Параметрические цепи реализуются на базе резисторов, емкостей и индуктивностей, значения которых ![]() изменяются во времени.
изменяются во времени.
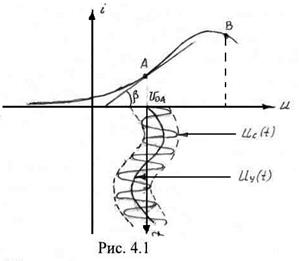 Параметрический резистор
Параметрический резистор ![]() , сопротивление которого изменяется во времени по заданному закону и вместе с тем не зависит от величины входного сигнала, может быть реализован на базе безынерциального нелинейного элемента с вольт-амперной характеристикой
, сопротивление которого изменяется во времени по заданному закону и вместе с тем не зависит от величины входного сигнала, может быть реализован на базе безынерциального нелинейного элемента с вольт-амперной характеристикой ![]() , на вход которого подается сумма преобразуемого сигнала
, на вход которого подается сумма преобразуемого сигнала ![]() и управляющего напряжения
и управляющего напряжения ![]() (рис. 4.1).
(рис. 4.1).
Положение рабочей точки А на характеристике ![]() определяется постоянным напряжением смещения
определяется постоянным напряжением смещения ![]() . Так как напряжение сигнала гораздо меньше напряжения смещения
. Так как напряжение сигнала гораздо меньше напряжения смещения ![]() , то такой слабый сигнал можно считать малым приращением по отношению к
, то такой слабый сигнал можно считать малым приращением по отношению к ![]() и сопротивление нелинейного элемента по отношению к сигналу оценивать дифференциальным сопротивлением
и сопротивление нелинейного элемента по отношению к сигналу оценивать дифференциальным сопротивлением
![]() . (4.2)
. (4.2)
Величина, обратная ![]() , как известно, называется дифференциальной крутизной
, как известно, называется дифференциальной крутизной
![]() . (4.3)
. (4.3)
Если, например, ВАХ нелинейного элемента аппроксимируется полиномом:
![]() ,
,
где ![]() ,
,
то в соответствии с (4.3), получим
![]() ,
,
или, учитывая, что ![]()
![]() .
.
Ток, вызванный полезным сигналом
![]() .
.
Таким образом, по отношению к сигналу справедливо условие (4.1) и по отношению к сигналу нелинейный элемент ведет себя как линейный, но с переменной крутизной.
Существенной особенностью параметрического резистора является то, что его сопротивление или крутизна могут быть отрицательными. Это имеет место при выборе рабочей точки на спадающем участке вольт-амперной характеристики (точка В на рис. 4.1).
Переменную управляемую емкость в параметрических цепях реализуют при помощи специальных полупроводниковых диодов, называемых варикапами. Работа этих диодов основана на следующем эффекте: если к ![]() переходу диода приложено напряжение обратной полярности, то разделенный заряд
переходу диода приложено напряжение обратной полярности, то разделенный заряд ![]() в запирающем слое является нелинейной функцией приложенного напряжения
в запирающем слое является нелинейной функцией приложенного напряжения ![]() . Зависимость
. Зависимость ![]() называют кулон-вольтовой характеристикой
называют кулон-вольтовой характеристикой
![]() , (4.4)
, (4.4)
где ![]() – значение емкости.
– значение емкости.
Так же, как и сопротивление резистора, емкость может быть статической и дифференциальной. Дифференциальная емкость определяется следующим образом
![]() . (4.5)
. (4.5)
Здесь ![]() – исходное запирающее напряжение варикапа.
– исходное запирающее напряжение варикапа.
При изменении напряжения, приложенного к варикапу (конденсатору) возникает ток:
![]() . (4.6)
. (4.6)
Очевидно, чем больше запирающее напряжение, тем больше величина обратного ![]() перехода, тем меньше значение
перехода, тем меньше значение ![]() .
.
Переменную управляемую индуктивность в параметрических цепях можно реализовать на базе катушки индуктивности с ферромагнитным сердечником, магнитная проницаемость которого зависит от величины подмагничивающего тока ![]() . Однако, вследствие большой инерционности процессов перемагничивания материала сердечника, переменные управляемые индуктивности не нашли применения в параметрических радиотехнических цепях.
. Однако, вследствие большой инерционности процессов перемагничивания материала сердечника, переменные управляемые индуктивности не нашли применения в параметрических радиотехнических цепях.
4.2. Параметрическое усиление сигналов
На практике широкое распространение получили параметрические цепи с переменной емкостью, которая является элементом колебательного контура. В качестве управляемой емкости выступает варикап. При определенных условиях параметрически управляемый конденсатор может выступать своего рода «посредником», передающим часть энергии внешнего управляющего источника цепям, несущим полезный сигнал. Так как при этом, в контур поступает энергия от внешнего источника, потери в контуре при выделении полезного сигнала могут быть частично скомпенсированы. Процесс внесения энергии в контур называется накачкой энергии, а внешний источник – генератором накачки.
Установим связь между емкостью конденсатора и запасенной в нем энергией. Известно, что энергия конденсатора емкостью ![]() определяется соотношением
определяется соотношением
![]() . (4.7)
. (4.7)
Пусть емкость конденсатора получила малое приращение ![]() . Это вызовет изменение энергии
. Это вызовет изменение энергии ![]() . Продифференцировав (4.7), получим
. Продифференцировав (4.7), получим
![]() ,
,
или с учетом (4.7)
![]() ,
,
откуда следует
![]() . (4.8)
. (4.8)
 Из этого выражение следует, что увеличение емкости конденсатора приводит к уменьшению энергии в нем и наоборот.
Из этого выражение следует, что увеличение емкости конденсатора приводит к уменьшению энергии в нем и наоборот.
Рассмотрим контур, образованный постоянной индуктивностью ![]() , параметрической емкостью
, параметрической емкостью ![]() и сопротивлением потерь
и сопротивлением потерь ![]() . Положим сначала, что величина параметрической емкости не меняется и равна
. Положим сначала, что величина параметрической емкости не меняется и равна ![]() . Тогда резонансная частота контура
. Тогда резонансная частота контура
![]() .
.
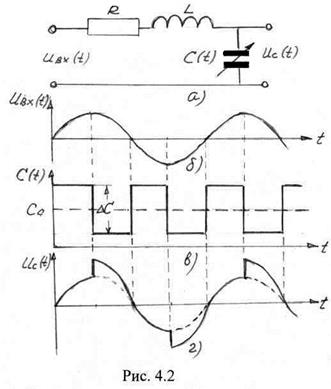
Если подать на вход контура напряжение
![]() ,
,
при ![]() (рис. 4.2б), то выходное напряжение будет равно (пунктир на рис.4.4г):
(рис. 4.2б), то выходное напряжение будет равно (пунктир на рис.4.4г):
![]() .
.
Будем теперь периодически изменять (модулировать) значение емкости ![]() напряжением генератора накачки с частотой
напряжением генератора накачки с частотой ![]() , т.е. вдвое большей частоты полезного сигнала.
, т.е. вдвое большей частоты полезного сигнала.
Будем полагать, что изменение емкости ![]() на величину
на величину ![]() происходит скачкообразно, причем при достижении экстремальных значений выходного сигнала емкость конденсатора уменьшается, а при переходе через ноль – увеличивается (рис. 4.2в). Так как при уменьшении емкости конденсатора согласно (4.8) происходит увеличение энергии в нем, а это увеличение осуществляется за счет внешнего источника (генератора накачки), напряжение на емкости в моменты достижения экстремальных значений увеличивается (рис. 4.2г). В то же время увеличение емкости происходит в моменты перехода через ноль входного сигнала и привлечения энергии со стороны генератора накачки, равно как и отдачи энергии во внешние цепи не происходит. Таким образом, при такой накачке будет осуществляться однонаправленный приток энергии в колебательный контур.
происходит скачкообразно, причем при достижении экстремальных значений выходного сигнала емкость конденсатора уменьшается, а при переходе через ноль – увеличивается (рис. 4.2в). Так как при уменьшении емкости конденсатора согласно (4.8) происходит увеличение энергии в нем, а это увеличение осуществляется за счет внешнего источника (генератора накачки), напряжение на емкости в моменты достижения экстремальных значений увеличивается (рис. 4.2г). В то же время увеличение емкости происходит в моменты перехода через ноль входного сигнала и привлечения энергии со стороны генератора накачки, равно как и отдачи энергии во внешние цепи не происходит. Таким образом, при такой накачке будет осуществляться однонаправленный приток энергии в колебательный контур.
Проведем спектральный анализ тока, протекающего через параметрический конденсатор в цепи (рис. 4.3а) образованной источником напряжения сигнала
![]() , (4.9)
, (4.9)
и управляемым конденсатором, емкость которого изменяется во времени по гармоническому закону с частотой накачки:
![]() , (4.10)
, (4.10)
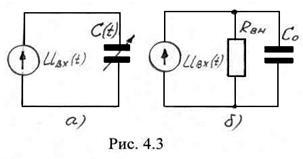 где
где ![]() – коэффициент, характеризующий глубину модуляции емкости.
– коэффициент, характеризующий глубину модуляции емкости.
Так как заряд в конденсаторе:
![]() ,
,
то ток, протекающий через конденсатор
![]() . (4.11)
. (4.11)
Подстановка (4.9) и (4.10) в (4.11) после выполнения операций дифференцирования и использования тригонометрических соотношений
![]() ;
;
![]() ,
,
позволяет получить выражение для ![]() , которое приведено полностью в [л.4] с. 318.
, которое приведено полностью в [л.4] с. 318.
Спектр тока содержит составляющую частоты ![]() и две боковые составляющие на частотах
и две боковые составляющие на частотах ![]() и
и ![]() . При этом полезной составляющей, которая выделяет мощность на конденсаторе, является составляющая разностной частоты, которая при
. При этом полезной составляющей, которая выделяет мощность на конденсаторе, является составляющая разностной частоты, которая при ![]() , описывается выражением
, описывается выражением
![]() .
.
Средняя мощность, выделяемая на конденсаторе за период ![]() входного сигнала
входного сигнала
![]() . (4.12)
. (4.12)
Обозначая ![]() ;
; ![]() ;
; ![]() , (4.13)
, (4.13)
выражение (4.12) можно представить следующим образом
![]() . (4.14)
. (4.14)
В соответствии с (4.14) параметрический конденсатор можно представить в виде параллельного соединения емкости ![]() и сопротивления
и сопротивления ![]() , т.е. активного сопротивления, вносимого в цепь. При этом, в зависимости от величины угла
, т.е. активного сопротивления, вносимого в цепь. При этом, в зависимости от величины угла ![]() (от соотношения между начальной фазой входного сигнала, которое в данном рассмотрении полагается равной
(от соотношения между начальной фазой входного сигнала, которое в данном рассмотрении полагается равной ![]() и начальной фазой генератора накачки
и начальной фазой генератора накачки ![]() ) вносимое сопротивление может принимать как положительное, так и отрицательное значения. Очевидно, при
) вносимое сопротивление может принимать как положительное, так и отрицательное значения. Очевидно, при ![]() параметрически управляемый конденсатор поставляет в цепь энергию на частоте входного сигнала.
параметрически управляемый конденсатор поставляет в цепь энергию на частоте входного сигнала.
Рассмотренное свойство параметрически управляемого конденсатора позволяет строить как усилители, так и генераторы сигналов.
Схема одноконтурного параметрического усилителя изображена на рис. 4.4 а). Напряжение входного сигнала поступает на контур ![]() , настроенный на частоту
, настроенный на частоту ![]() . Для согласования источника сигнала используется частичное включение контура (точки 1-2). Напряжение генератора накачки поступает на вход контура
. Для согласования источника сигнала используется частичное включение контура (точки 1-2). Напряжение генератора накачки поступает на вход контура ![]() , настроенного на частоту
, настроенного на частоту ![]() .
.
Очевидно, контур ![]() является фильтром только частоты
является фильтром только частоты ![]() , а контур
, а контур ![]() – фильтром частоты
– фильтром частоты ![]() . Таким образом, эти фильтры разделяют источники входного сигнала и сигнала генератора накачки. Постоянное напряжение
. Таким образом, эти фильтры разделяют источники входного сигнала и сигнала генератора накачки. Постоянное напряжение ![]() создает среднюю емкость варикапа
создает среднюю емкость варикапа ![]() . Выходное напряжение снимается с контура
. Выходное напряжение снимается с контура ![]() (точки 1-3).
(точки 1-3).
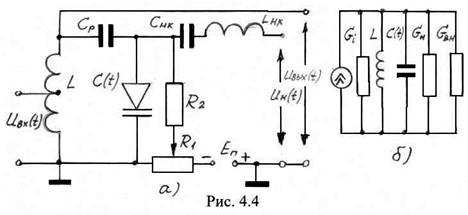 Для анализа параметрического усилителя составим его эквивалентную схему (рис. 4.4 б), в которой вместо источника ЭДС сигнала
Для анализа параметрического усилителя составим его эквивалентную схему (рис. 4.4 б), в которой вместо источника ЭДС сигнала ![]() используем генератор тока с внутренней проводимостью
используем генератор тока с внутренней проводимостью ![]() , подключенный параллельно контуру
, подключенный параллельно контуру ![]() с проводимостью нагрузки
с проводимостью нагрузки ![]() и вносимой проводимостью
и вносимой проводимостью ![]() . При
. При ![]() согласно (4.13) вносимая проводимость
согласно (4.13) вносимая проводимость ![]() принимает отрицательное значение, суммарная проводимость уменьшается, что приводит к повышению добротности контура и обеспечивает эффект усиления.
принимает отрицательное значение, суммарная проводимость уменьшается, что приводит к повышению добротности контура и обеспечивает эффект усиления.
Коэффициент усиления параметрического усилителя определяется как отношение мощности сигнала при модуляции параметрического конденсатора ![]() к мощности при отсутствии модуляции.
к мощности при отсутствии модуляции.
Напряжение на зажимах генератора тока, т.е. на контуре, равно
![]() .
.
Мощность, выделяемая в нагрузке
![]() .
.
Максимальная мощность, как известно, выделяется при согласовании генератора с нагрузкой, т.е. при ![]() (или
(или ![]() ). Тогда
). Тогда
![]() . (4.15)
. (4.15)
При отсутствии параметрической модуляции ( ![]() ) максимальная мощность
) максимальная мощность
![]() . (4.16)
. (4.16)
Коэффициент усиления параметрического усилителя, как было показано выше
![]() . (4.17)
. (4.17)
Подстановка (4.15) и (4.16) в (4.17) после несложных преобразований дает
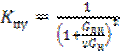 .
.
Так как ![]() при параметрическом усилении отрицательно, коэффициент усиления параметрического усилителя всегда больше единицы.
при параметрическом усилении отрицательно, коэффициент усиления параметрического усилителя всегда больше единицы.
В заключение следует отметить, реализация параметрического усиления требует строгого выполнения соотношений между начальными фазами входного сигнала и сигнала генератора накачки или, иными словами, тщательной синхронизации источника сигнала и генератора накачки.

