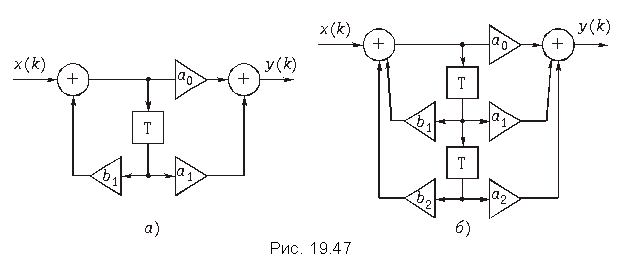
Звенья 1-го и 2-го порядков. В литературе типовыми звеньями дискретных цепей считаются звенья 1-го и 2-го порядков. Они получаются из общей структуры рис. 19.41, если оставить в ней только один либо два элемента задержки.

На рис. 19.47, а показано звено 1-го порядка с передаточной функцией

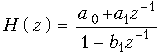
и АЧХ

.

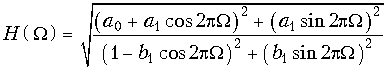Типовое звено 2-го порядка изображено на рис. 19.47, б. Его передаточная функция

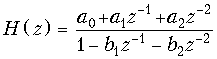
и АЧХ

Пример. Построим график АЧХ звена первого порядка, у которого a₀ = 1, a₁ = 0.

Передаточная функция такого звена первого порядка

Амплитудно-частотная характеристика

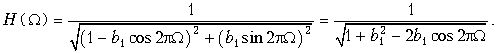
Поскольку полюс z_n передаточной функции H(z) равен b₁, то для того, чтобы цепь была устойчивой необходимо выбирать значения b₁ такими, чтобы выполнялось условие |b₁| < 1.

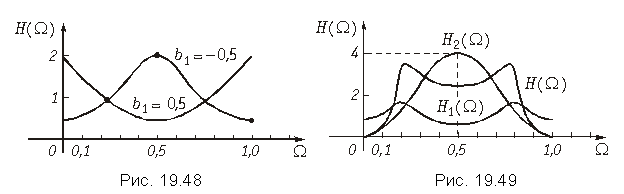
На рис. 19.48 приведены графики АЧХ, построенные для значений b₁ = 0,5 и b₁ = –0,5.

АЧХ рассматриваемого фильтра зависит от знака коэффициента b₁. При b₁ > 0 получаем режекторный фильтр, при b₁ < 0 – полосовой.

Пример. Найдем передаточную функцию и построим график АЧХ звена 2-го порядка (рис. 19.47, б) при a₀ = a₂ = 1, a₁ = 2, b₁ = 0,2 и b₂ = –0,4.

Передаточная функция такого звена

.

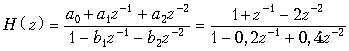Как указывалось ранее, рекурсивную цепь с прямыми и обратными связями можно представить как каскадное соединение рекурсивного фильтра с передаточной функцией H₁(z) и нерекурсивного фильтра с передаточной функцией H₂(z). В нашем случае, для звена второго порядка,

График АЧХ для H₂(z) уже был построен и приведен на рис. 19.46. АЧХ H₁(W) рекурсивного фильтра рассчитывается по формуле

.

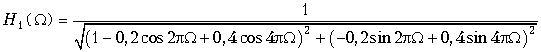Графики H₁(W), H₂(W) и H(W) = H₁(W)×H₂(W) изображены на рис. 19.49.

Соединение типовых звеньев. Типовые звенья могут соединяться каскадно (рис. 19.50, а); при этом их передаточные функции перемножаются:

,

где H₁, H₂, H₃ – передаточные функции звеньев.

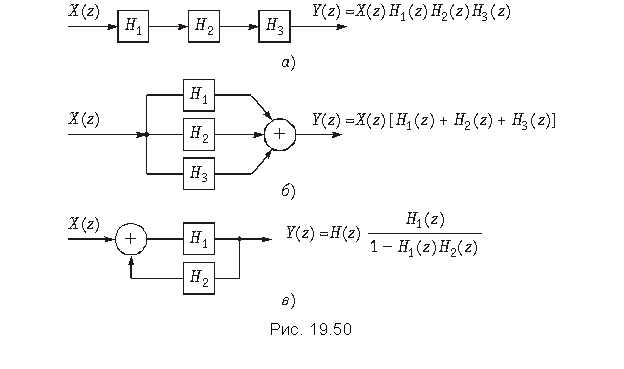
При параллельном соединении звеньев (рис. 19.50, б) общая передаточная функция определяется как

.

Соединение, показанное на рис. 19.50, в, называют включением цепи H₂ в обратную связь цепи H₁, причем

.

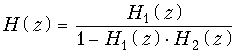Следует иметь в виду, что все соединения, изображенные на рис. 19.50, справедливы не только для типовых звеньев, но и для любых других структур.

Пример. Найдем передаточные функции при различных способах соединения рекурсивной и нерекурсивной цепей, имеющих и .

При каскадном соединении этих цепей

;

при параллельном соединении

;

при включении цепи H₂ в обратную связь цепи H₁

.

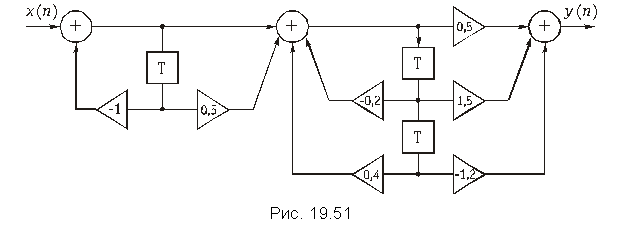
Пример. Найдем передаточную функцию дискретной цепи, изображенной на рис. 19.51.

Цепь, приведенная на рис. 19.51, представляет собой каскадное соединение типовых звеньев 1-го и 2-го порядков. Передаточная функция соединения имеет вид

.

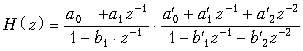Подставляя в выражение для H(z) заданные значения коэффициентов усиления a₀ = 1, a₁ = 0,5, b₁ = –1 и = 0,5, = 1,5, = –1,2, = –0,2, = 0,4, получаем

.