Рассмотрим структуру дискретной цепи, подобную рис. 35 и 39, но содержащую N элементов задержки. Она приведена на рис. 40,а и б. Здесь коэффициенты усиления , , , ..., представляют собой отсчеты дискретной импульсной реакции , т.е.

.

Из структуры рис. 40,а следует, что

. (18)

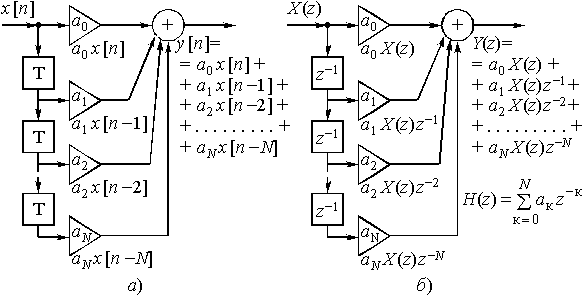
Рис. 40

Переход к z-изображениям (рис. 40, б) дает выражение:

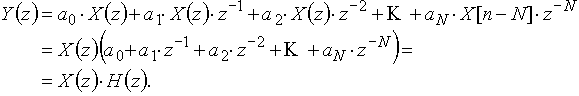
Передаточная функция этой дискретной цепи есть

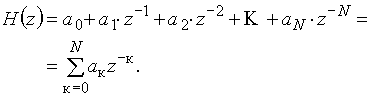(19)

Дискретные цепи со структурой рис. 40,а и б и передаточной функцией вида (19) называются нерекурсивными цепями.

Пример 15.1. Найдем выходную последовательность и передаточную функцию нерекурсивной цепи, структурная схема которой приведена на рис. 41.

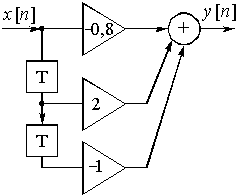
Рис. 41

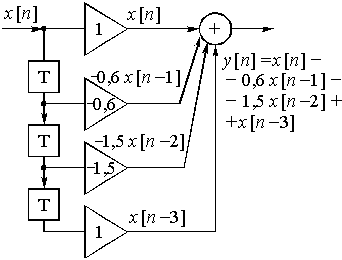
Рис. 42

Выходная последовательность в соответствии с уравнением (18) имеет вид

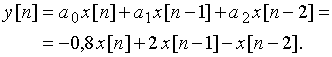
Передаточную функцию цепи найдем, используя уравнение (19) или непосредственно по схеме

.

Пример 15.2. Найдем отсчеты выходного сигнала нерекурсивной дискретной цепи, имеющей дискретную импульсную реакцию = {1; -0,6; -1,5; 1}, при воздействии не нее дискретного сигнала = {1; 0; 1; 0}.

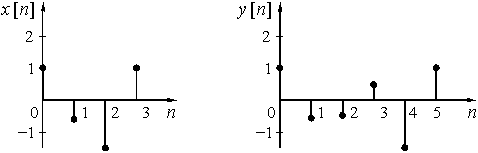
Рис. 43

Отсчеты дискретной импульсной характеристики - это коэффициенты усиления ; ; ; . Структурная схема нерекурсивной дискретной цепи с заданной импульсной реакцией приведена на рис. 42.

Выходной дискретный сигнал найдем, используя выражение (19)

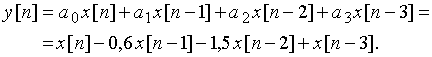
Отсчеты сигнала найдем, подставляя значения в полученное разностное уравнение.

;

;

;

.

Аналогичным образом рассчитываем ; ; . Все остальные отсчеты также равны нулю.

Таким образом, выходная последовательность = {1; -0,6; -0,5; 0,4; -1,5; 1}. Графики и приведены на рис. 43.

Иного рода дискретная цепь показана на рис. 44,а и б.

Как следует из (рис. 44,а), выходной сигнал

. (20)

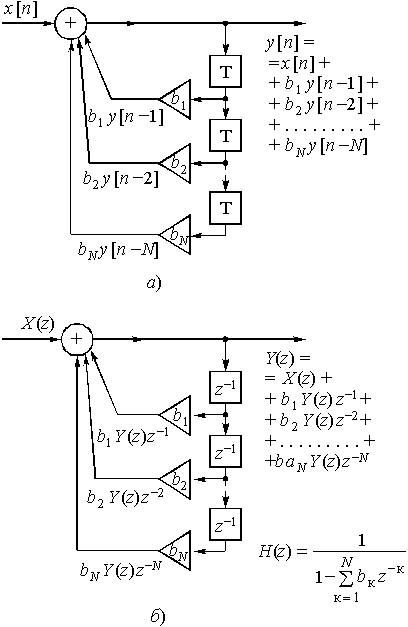
Рис. 44

Формула (20) позволяет вычислить текущий отсчет выходного сигнала не только по текущему отсчету входного сигнала, но и по предыдущим (задержанным) N отсчетам , , ..., выходного сигнала. Подобные формулы, в отличие от (18), где используются текущий и задержанные отсчеты только входного сигнала, в математике получили название рекурсивных. Поэтому и цепь, реализующая алгоритм (20), называется рекурсивной.

Z-преобразование выражения (20) имеет вид:

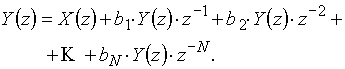(21)

Эта же запись следует непосредственно из рис. 44,б.

Передаточную функцию рекурсивной цепи получаем из (21):

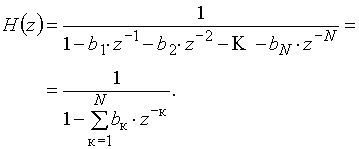(22)

Пример 15.3. Структурная схема рекурсивной дискретной цепи приведена на рис. 45. Найдем передаточную функцию, импульсную характеристику и реакцию цепи на дискретное воздействие = {1; -1; 1}.

Передаточную функцию цепи найдем, используя формулу (22)

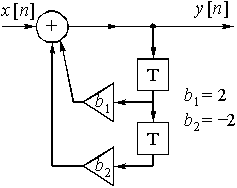
Рис. 45

Для нахождения дискретной импульсной характеристики рассчитаем реакцию цепи на дискретную d-функцию, т.е. на сигнал = = {1; 0; 0; ...}. С учетом формулы (20) получаем, что дискретная импульсная характеристика цепи (рис. 45) имеет вид

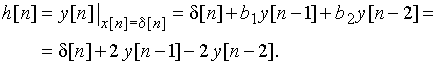
Отсчеты равны соответственно = 1; = 2; = = 2; = 0 и т.д.

Для расчета реакции цепи на сигнал также воспользуемся разностным уравнением (20):

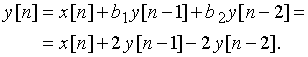
Найдем отсчеты :

;

;

;

;

; ; и т.д.

Если выход дискретной цепи рис. 40,а подключить ко входу цепи, изображенной на рис. 44,а, то полученная цепь будет описываться уравнением

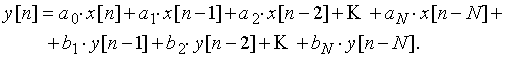(23)

Для получения передаточной функции можно либо выполнить z-преобразование выражения (23), либо перемножить передаточные функции (19) и (22) каскадно включенных структур:

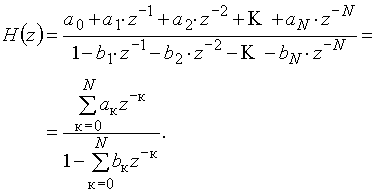(24)

Рис. 46

Можно изменить порядок каскадного включения нерекурсивной и рекурсивной цепей на обратный. Получится схема, показанная на рис. 46,а. Передаточная функция этой новой структуры, естественно, будет по-прежнему описываться выражением (24), а временной алгоритм - формулой (23). Заметим, что на выходах параллельных элементов задержки будут одни и те же сигналы. Следовательно, реально необходимо иметь лишь один из двух элементов задержки. Соответствующая эквивалентная дискретная цепь изображена на рис. 46, б; она называется канонической, потому что в ней используется минимально возможное число элементов задержки. Так как схема рис. 46,б содержит и рекурсивную часть, в литературе ее часто также называют рекурсивной дискретной цепью.

Пример 15.4. Определим передаточную функцию цепи, приведенной на рис. 47.

Для рекурсивной цепи с прямыми и обратными связями (рис. 47) запишем коэффициенты усиления усилителей:

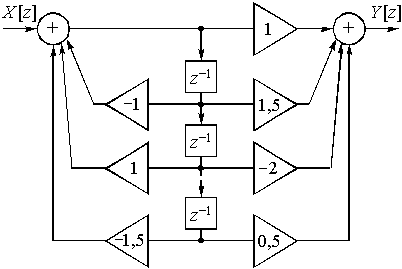
Рис. 47

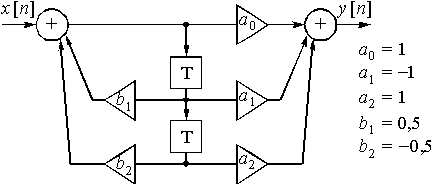
Рис. 48

= 1; = 1,5; = -2; = 0,5;

= -1; = 1; = -1,5.

Определим передаточную функцию цепи (рис. 47), подставляя значения коэффициентов усиления в выражение (24),

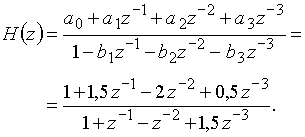
Пример 15.5. Найдем реакцию дискретной цепи на воздействие = {1; -1; 1; -1}, если передаточная функция цепи имеет вид .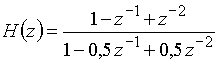

Составим структурную схему дискретной цепи с заданной передаточной функцией (рис. 48). Коэффициенты усиления известны: = 1; = -1; = 1; = 0,5; = -0,5.

Найдем выходной сигнал цепи, используя уравнение (23) или непосредственно по схеме:

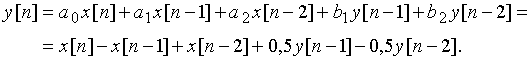
Рассчитаем отсчеты :

;

;

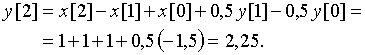
Аналогичным образом рассчитываем , и т.д.

Самоконтроль

1. Какие дискретные цепи называются нерекурсивными?

2. Какие дискретные цепи называются рекурсивными?

3. Как рассчитываются передаточные функции нерекурсивных и рекурсивных дискретных цепей?

4. Как рассчитывается выходной сигнал дискретной цепи?

5. Составьте схемы дискретных цепей, имеющих передаточные функции

а) ;

б) ;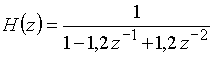

в) ;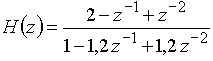

г) .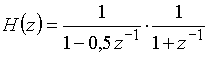

6. Запишите разностные уравнения для цепей, имеющих передаточные функции, приведенные в 5, а; 5, б и 5, в.