8.3.1. Однотактная схема двухконтурная ВКС

8.3.2. Двухтактная схема двухконтурная ВКС

8.3.3. Расчет мощности высших гармоник на выходе одиночного П-контура, используемого в качестве нагрузки ОК (при АМ - программа РCAМ0F)

Можно показать, что максимальное значение мощности n-ой гармоники рабочей частоты на входе антенного фидера с волновым сопротивлением W и КБВ на рабочей частоте и на n-ой гармонике, равными соответственно К_ф1 и К_n определяется выражением [6]:

P_nmax = 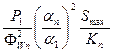, (8.53)

где Р₁–мощность на рабочей частоте, α₁ и α_n–коэффициенты разложения косинусоидального импульса анодного тока лампы оконечного каскада соответственно для первой и n-ой гармоник, К_n– КБВ в фидере на n-ой гармонике, Φ_wn - коэффициент фильтрации n–ой гармоники, обеспечиваемый выходной колебательной системой, который принимают равным:

= , (8.54)

где I_a1 и I_аn – токи рабочей частоты и ее n-ой гармоники на входе колебательной системы, I_w1 иI_wn - токи рабочей частоты и ее n-ой гармоники на входе согласованного на рабочей частоте антенного фидера, т.е. в нагрузке, сопротивлении

которой равно W. Отношение 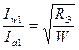, отношение определяется построением и настройкой конкретной колебательной системы.

Коэффициент S_max выражается формулой:

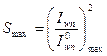(8.55)

Величина S_max, как и величина Φ_wn, определяется конкретной схемой выходной колебательной системы и способом ее регулировки на рабочей частоте. В (8.55)

–ток n – ой гармоники рабочей частоты, питающей согласованный антенный фидер, т.е. при КБВ в этом фидере на рабочей частоте К_ф1=1, a I_Wn- ток n - ой гармоники рабочей частоты, питающей антенный фидер c КБВ на рабочей частоте

К_ф1≠1. В общем случае S_max равен:

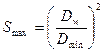, ( 8.55’)

где для схемы рис.3а:

D_w = (X_LПw· X_cвw· γ_2w)/X_c1= b_w ·X_cвw ·γ_2w ,

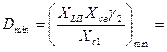(b·X_cв··γ₂)_min . (8.56)

Здесь Х_с1, Х _LП и Х_св – параметры выходного П - контура и реактивное сопротив

ление элемента связи при КБВ в фидере К_ф1≠1,

. (8.57)

Так как при КБВ К_ф1≠1 входное сопротивление антенного фидера изменяется в широких пределах, то для нахождения величины D_min необходим расчет величины D при всех возможных (при заданном КБВ К_ф1) значениях нагрузки колебательной системы, т.е. входного сопротивления антенного фидера. Эта задача решается ЭВМ.

Коэффициент фильтрации высших гармоник Φ_Wn колебательной системы, изображенной на рис.3а, при индуктивной связи между контурами определяется выражением:

(8.58)

Здесь R_э – эквивалентное сопротивление нагрузки лампы оконечного каскада;

– добротность анодного контура; коэффициенты γ₁, γ_2w и b_w равны:

,

,

b_w=X_LПw / X_C1w . (8.59)

- параметр выходного П-контура, величина которого задается при расчете колебательной системы, X_LПw, X_c1w и X_cвw- значения реактивных сопротивлений элементов П-контура и элемента связи при КБВ в фидере на рабочей частоте К_ф1=1. Из формулы для Φ_Wn видно, что при емкостной связи между контурами коэффициент фильтрации по крайней мере в n² раз меньше, чем при индуктивной, а мощность n-ой гармоники на выходе колебательной системы – в n⁴ раз больше.

8.3.1. Однотактная схема двухконтурная ВКС

Расчет коэффициента фильтрации высших гармоник Φ_wn и мощности высших гармоник P_nmax на выходе колебательной системы однотактного оконечного каскада передатчика производится по формулам (8.53)-(8.59).

8.3.2. Двухтактная схема двухконтурная ВКС

Как известно, в двухтактной схеме аноды ламп на четных гармониках находятся под одинаковым потенциалом, при этом двухтактное включение ламп равносильно параллельному, поэтому эквивалентная схема выходной двухконтурной колебательной системы для четных гармоник при построении ОК передатчика по двухтактной схеме может быть представлена рис.8.3г (в таких схемах катушка индуктивности анодного контура не имеет заземленной средней точки). На вход колебательной системы здесь поступает сумма четных гармоник анодного тока генераторных ламп обоих плеч схемы. Нагрузкой колебательной системы на четных гармониках является участок фидера, проходящий внутри здания, где установлен передатчик. Волновое сопротивление этого участка на четных гармониках W^* зависит от его конструкции. При синфазном питании оно равно либо W^*= 0,25W_ф, либо W^*= 0,5W_ф, где W_ф- волновое сопротивление антенного фидера.

Коэффициент фильтрации четных высших гармоник, питающих антенный фидер синфазно, равен:

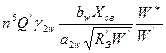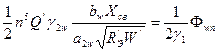= = , (8.60)

(в двухтактных схемах катушка индуктивности анодного контура не имеет заземленной средней точки). Здесь R^’_э - эквивалентное сопротивление нагрузки генераторной лампы одного плеча двухтактной схемы,W’=0,5W_ф. Обычно в оте-чественных передатчиках волновое сопротивление W^*= 0,25W, при этом в формуле (60) W^*/W’ = 0,5, поэтому =0,5Φ_wn, где Φ_wn определяется формулой (8.58). Все коэффициенты в (8.58) рассчитываются для одного плеча двухтактной схемы колебательной системы.

Мощность высших гармоник на входе антенного фидера равна:

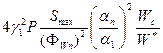= , (8.61)

здесь Р – колебательная мощность на рабочей частоте, W_с ≈ 300 Ом – волновое сопротивление антенного фидера, а = , где К_n – КБВ в антенном фидере на четных гармониках, питающих его синфазно. Величина S_max также рассчитывается для одного плеча схемы.

8.3.3. Расчет мощности высших гармоник на выходе одиночного П-контура, используемого в качестве нагрузки ОК (при АМ - программа РCAМ0F)

Одиночные П-контура используют только в однотактных схемах ОК передатчиков. Коэффициент фильтрации П-контура определяется формулой:

= , (8.62)

где γ_2w и b_w определяются (8.56) при К₁=1, а k_r0= - коэффициент трансформации сопротивления П-контура, нагруженного согласованным фидером. Максимальная мощность высших гармоник на входе антенного фидера равна:

P_nmax=P_~1S_max 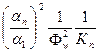, (8.63)

где К_n- КБВ в фидере на n-ой гармонике, S_max определяется ( 8.55’). Для схемы

рис.8.3а:

D_w = (X_LПw· γ_2w)/X_c1w= b_w ·γ_2w ,

D_min= (X_LП ·γ₂)/X_c1=(b·γ₂)_min . (8.64)