2.3.1. Основы геометрической оптики

2.3.2. Анализ лучевого распространения света в волоконных световодах

2.3.1. Основы геометрической оптики

Геометрическая оптика имеет историю, датируемую двумя тысячами лет, и предполагает, что свет состоит из лучей, распространяющихся от источника по прямым линиям в гомогенной среде, например стекле, воде, воздухе или вакууме. При этом в геометрической оптике принято утверждение, что плоские волновые фронты распространяются под прямыми углами к каждому лучу и свет уменьшается пропорционально квадрату расстояния.

В общем случае под скоростью света понимают скорость электромагнитной энергии в вакууме. В других материалах (например, в стекле) свет распространяется с меньшей скоростью. При перемещении из одного материала в другой изменяется скорость распространения, что, с точки зрения волновой теории, приводит к изменению направления движения. Отклонение света от прямого направления называется преломлением. Волны с различными длинами в одном и том же материале распространяются с различными скоростями. Зависимость скорости от длины волны имеет важное значение в волоконной оптике.

Как известно, луч света при падении на границу раздела двух сред делится на отраженный и преломленный. Согласно закону отражения луч света, который падает на границу раздела двух сред, отражается под тем же самым углом (φ_отр) к нормали (перпендикуляру к границе), что и угол падения (φ_n) к поверхности, т.е. φ_n = φ_отр .

Согласно закону Снеллиуса (закон преломления) лучи света, падающие на границу раздела двух сред, имеют углы преломления, отличные от углов падения к нормали границы этих сред. Связь этих углов определяется выражением:

n₁sin φ_1п=n₂sin φ_1пр , (2.4)

где n₁ и n₂ — показатели преломления первой и второй сред, соответственно.

Показатели преломления n (величина безразмерная) выражается через отношение скорости света в вакууме (с) к скорости света в материале (v):

(2.5)

Показатели преломления различных веществ и скорости распространения света в них [2] приведены в табл. 2.2.

Таблица 2.2. Показатели преломления различных материалов

Особый интерес для волоконной оптики представляет тот факт, что показатель преломления стекла может из меняться в зависимости от его состава. Количество отраженного света от границы двух сред зависит от их показателей преломления. Если излучение видимой области спектра падает на границу раздела двух сред и переходит из оптически более плотной среды n₁на оптически менее плотную n₂ (n₂< n₁) и угол падения увеличивается, то угол преломления приближается к 90^о. Увеличивая угол падения, можно добиться такого состояния, при котором преломленный луч будет располагаться вдоль границы раздела сред, не переходя в другую среду.

Угол падения при этом называется критическим углом (φ_кр) полного внутреннего отражения, т.е. угол падения, при котором угол преломления равен 90^о, называется критическим углом. Если угол падения больше критического, то свет полностью отражается в исходную среду, не проникая в другой материал. При этом имеет место только отражение, а преломление отсутствует, что приводит к полному внутреннему отражению, т.е. при φ_1пр =90^о

(2.6)

На этом явлении основан принцип передачи оптического излучения по волоконным световодам.

Рассмотрим отражение света при угле падения, равном 90^о. Даже когда свет проходит в более плотную среду, некоторая его часть отражается в исходную среду. Этот эффект получил название отражение Френеля. Чем больше разница показателей преломления сред, тем большая доля света отражается назад. Показатель Френелевского отражения на границе с воздухом

(2.7)

В децибелах потери переданного света составляют:

А = 10lg(1- р). (2.8)

Примером последствий отражения Френеля могут служить потери на вводе и выводе оптического излучения в волоконный световод.

Для света, падающего из воздуха на границу стекла (с n=l,5 для стекла), потери от френелевского отражения равны примерно 0,17 дБ. Это значение зависит от состава стекла. Поскольку такого рода потери происходят как при входе света в стекло, так и при выходе из него, то потери на соединении двух стекол составляют 0,34 дБ.

Поляризованный свет. Свет может рассматриваться как волна, состоящая из двух полей, направленных перпендикулярно друг к другу: электрического поля и магнитного поля (рис. 2.9). Эти поля синхронны с полевыми векторами, с разностью фаз между собой в 90^о.

Нормальный свет имеет бесконечное число перпендикулярно колеблющихся плоскостей, распространяющихся в направлении перемещения света. Отражением и рефракцией свет может быть поляризован.

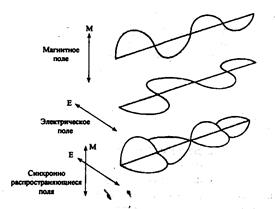
Рис. 2.9. Поля, составляющие свет: электрическое и магнитное

Свет, в котором интенсивность электрического поля остается неизменной, в то время как интенсивность магнитного поля уменьшается, назван ТЕ-поляризованным светом (коэффициент пропускания электрически поляризованного света). Свет, в котором интенсивность магнитного поля остается неизменной, в то время как интенсивность электрического поля уменьшается, называется ТМ-поляризованным светом (коэффициент пропускания поляризованного магнитного поля).

На рис. 2.10 показан пример поляризации света, падающего на поверхность некоторой кристаллической пластины, при этом электрическое и магнитное поля поляризуются по-разному.

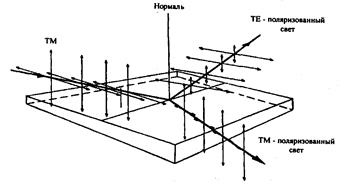
Рис. 2.10. Разложение падающего света с помощью пластины на поляризованные электрическое и магнитное поля

Два типа поляризации имеют несколько разные коэффициенты отражения, которые описываются законом отражения Френеля. Интенсивность отраженного света увеличивается от 4 % до 100 % при увеличении угла падения от 0 до 90^о для обеих поляризаций (преломленный свет уменьшается на эту же степень), но для ТМ-поляризации интенсивность сначала уменьшается с 4% до нуля, а затем снова увеличивается до 100 % (рис. 2.11). Угол, при котором ТМ-отражение является нулевым, называется углом Брюстера.

Принцип распространения света в стекловолокне основан на законе полного внутреннего отражения. При типичных значениях ПП в сердцевине n₁=1,47 и оболочке n₂=1,46 ОВ со ступенчатым ППП имеет критический угол полного внутреннего отражения φ_кр=83,3^о.

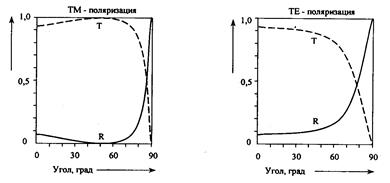
Рис. 2.11. Диаграммы зависимости коэффициентов отражения (R) и преломления (Т) различных поляризаций от угла падения света

Рис. 2.12. Рэлеевское рассеяние света из-за примесей в среде передачи

Рэлеевское рассеяние и свет Тиндаля. В аморфном материале типа стекла структура материала не везде однородна, поэтому стекло никогда полностью не будет прозрачно. Световой луч, распространяющийся через такой материал, рассеивается в направлениях (например, луч солнечного света в пыльном или заполненном дымом помещении) (рис. 2.12). Это явление называется рэлеевским рассеянием и вызвано присутствием в среде маленьких частиц и неоднородностей. Рассеянный свет называется светом Тиндаля. Гидроксильная группа (ОН^--), ионы металлов, примеси и т.д. объясняют это явление в стекловолокне.

Рэлеевское рассеивание — это то, что дает небу его синий цвет и солнцу его красный цвет на восходе и на закате. Эти цветные явления вызваны рассеиванием света молекулами воздуха. Молекулы и вариации неоднородностей в стекле функционируют как электрические диполь, излучающие поле.

В атмосфере коротковолновый свет (синий конец спектра) рассеивается в 3-4 раза больше, чем длинноволновый свет (красный конец спектра), который придает небу различные цвета в зависимости от положения солнца на небе. Лорд Рэлей объяснил это явление и показал, что рассеяние имеет решающее значение в выборе диапазона волн в волоконной оптике. Чем больше длина волны, тем меньше потери от рэлеевского рассеяния.

2.3.2. Анализ лучевого распространения света в волоконных световодах

В геометрической оптике световые волны изображаются лучами, направленными по нормали к волновой поверхности. При падении световой волны на плоскую границу раздела двух диэлектриков с разными значениями относительной диэлектрической проницаемости (ε) в общем случае наблюдаются прошедшая (преломленная) и отраженная волны. В соответствии с законом Снеллиуса угол падения связан с углами отражения и преломления с помощью равенства φ_п= φ_отр и выражения (2.4). Поскольку в оптических средах отношение магнитной проницаемости (μ) к магнитной проницаемости вакуума (μ₀) принимается равным единице, то в этом выражении а . В ОВ среда сердцевины более плотная, чем среда оболочки, т.е. n₁>n₂, поэтому при угле падения φ_п> φ_кр свет полностью отражается от границы сердцевина — оболочка и распространяется только в сердцевине волокна. Как известно, критический угол падения света определяется выражением:

(2.9)

Поток энергии из первой среды во вторую в среднем равен нулю, и энергия падающей электромагнитной волны полностью возвращается в первую среду.

В качестве примера рассмотрим ОВ со ступенчатым профилем показателя преломления. Ступенчатое оптическое волокно (рис. 2.13) представляет собой двухслойную стеклянную нить, сердцевина которой изготовлена из стекла с показателем преломления n₁ диаметром 2a=(3...50) мкм, а оболочка имеет показатель преломления n₂ и диаметр 2b=125 мкм. Для обеспечения полного внутреннего отражения на границе раздела необходимо, чтобы n₁>n₂. Поверх оболочки накладывается защитное покрытие с показателем преломления n₃< n₂.

На рис. 2.13 световые лучи, описывающие однородные плоские волны, пучком исходят от точечного источника, расположенного на оси волокна. На торце ОВ этот пучок лучей преобразуется в два типа лучей волокна: меридиональные, которые пересекают ось волокна, и косые, которые не пересекают эту ось. На рис. 2.14 представлена траектория прохождения косого луча в ступенчатом ОВ.

Часть меридиональных и косых лучей, испытывая полное внутреннее отражение в местах падения на границу сердцевина — оболочка, распространяется зигзагообразно вдоль ОВ.

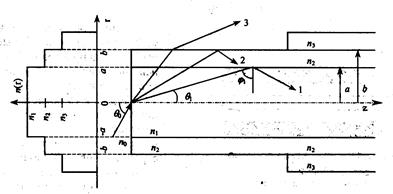
Рис. 2.13. Модель ОВ со ступенчатым профилем показателя преломления

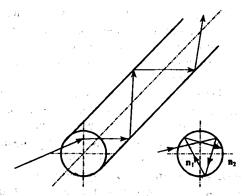
Рис. 2.14. Траектория прохождения косого луча в ОВ

Рассмотрим ход меридиональных лучей, падающих на входной торец ОВ и распространяю- щихся затем вдоль волокна (рис. 2.13). В зависимости от угла наклона луча θ₁ к оси Z меридиональные лучи, лежащие в плоскости рисунка, могут испытывать полное внутреннее отражение на границе сердечник — оболочка, если θ₁<arccos(n₂/n₁). При этом образуются моды сердечника 1, или направляемые моды. Если луч падает под углом arccos(n₂/n₁)< θ₁< arccos(n₃/n₂), то он может сформировать моду оболочки 2. Световые лучи, падающие под углом θ₁< arccos(n₃/n₂), излучаются в пространство, т.е. в защитную оболочку, образуя вытекающие моды, или моды излучения 3.

Луч, падающий на торец волокна из окружающей среды под углом θ₀ к оси волокна, преломляется при вхождении в сердцевину и распространяется в ней под углом θ₁ в соответствии с законом Снеллиуса:

(2.10)

При этом преломленный луч падает на боковую поверхность под углом φ₁=(π/2) – θ₁. Для полного внутреннего отражения лучей от боковой поверхности необходимо, чтобы φ₁≥φ_кр, где критический угол падения φ_кр определяется выражением (2.9). Следовательно, sinφ₁=cosθ₁≥n₂/n₁.

Из (2.10) следует, что

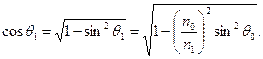
Таким образом,

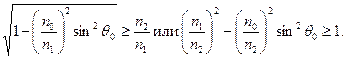
Однако , т.е.

(2.11)

Таким образом, если выполняется условие (2.11), то любой меридиональный луч распространяется вдоль сердцевины волокна. Это условие справедливо и для косых лучей.

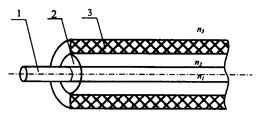
Рис. 2.15. Оптическое волокно: 1-сердцевина; 2-оболочка; 3-защитное покрытие

На рис. 2.15 представлена конструкция волокна в оболочке с защитным покрытием, в котором оптическое излучение распространяется в ОВ такой конструкции при выполнении условия n₁>n₂>n₃.. Соотношение между n₁ и n₂принято характеризовать относительной разностью ПП [4]

(2.12)

которая для большинства ОВ составляет 10^-2...10^-3. Показатель преломления оболочки имеет постоянное значение, а сердцевины — либо постоянное, либо изменяющееся по радиусу по определенному закону.

Изменение показателя преломления ОВ вдоль радиуса называется профилем показателя преломления.

Наличие оптической оболочки усложняет волновой процесс в ОВ. Часть меридиональных и косых лучей, многократно отражаясь от границы сердцевина — оболочка, распространяется вдоль сердцевины и образует моды сердцевины (направляемые моды). Остальные лучи, которые падают на эту границу под углами φ_п<φ_кр, уходят из сердцевины наружу. Лучи, покинувшие сердцевину, образуют моды излучения. Некоторые из них распространяются в оболочке за счет полного внутреннего отражения от границы оболочка — окружающая среда и образуют моды оболочки. Если защитное покрытие ОВ выполнено из сильно поглощающего материала, то оно устраняет перекрестные помехи между ОВ в оптическом кабеле, обусловленные модами излучения. Кроме того, защитное покрытие рассеивает энергию мод оболочки аналогично направляемым модам диэлектрического стержня. Как отмечалось выше, поле направляемых мод частично проникает в окружающую среду, где экспоненциально убывает, при этом глубина проникновения в оболочку ОВ, т.е. расстояние, на котором это поле убывает в е раз (е=2,718), определяется при φ_п>φ_кр выражением [5]:

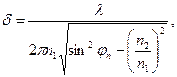(2.13)

где λ — длина волны оптического излучения, вводимого в ОВ.

Режим полного внутреннего отражения предопределяет условие подачи света на входной торец волоконного световода. Из рис. 2.16 видно, что световод пропускает лишь свет, заключенный в пределах телесного угла θ_А, величина которого обусловлена углом полного внутреннего отражения θ_В. Этот телесный угол θ_А характеризуется апертурой. Апертура-это угол между оптической осью и одной из образующих светового конуса, попадающего в торец волоконного световода, при котором выполняется условие полного внутреннего отражения. Обычно пользуются понятием числовой апертуры:

(2.14)

где n₀, n₁, n₂ — показатели преломления воздуха, сердечника, оболочки соответственно.

Имея в виду, что для воздуха n₀=1, получим

(2.15)

Как видно из рис. 2.16 между углом полного внутреннего отражения θ_В и апертурным углом падения луча θ_А имеется взаимосвязь. Чем больше угол θ_В, тем меньше апертура волокна θ_А. Для ступенчатых ОВ, используемых в системах связи, числовая апертура обычно равна 0,18 — 0,23.

Формула (2.15) учитывает только меридиональные лучи ОВ. Однако, в основном, в ОВ преобладают косые лучи, которые не пересекают ось, а распространяются по ломаным (для ступенчатого ОВ) или право- или левовинтовым спиралям (для градиентного ОВ).

Вывод простого выражения для числовой апертуры косых лучей очень сложен. Отметим только, что числовая апертура, подсчитанная для меридиональных лучей ступенчатого ОВ (2.15), меньше действительной числовой апертуры NA_Д, учитывающей все лучи. Отношение NA_Д /NA для различных значений ПП п₁и п₂, например в [5, 6], увеличивается с уменьшением разности п₁-п₂, т.е. с уменьшением апертуры NA меридиональных лучей.

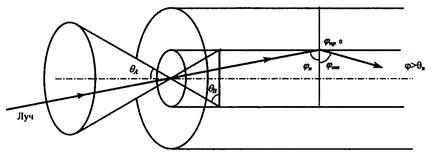
Рис. 2.16. Принцип действия ОВ

Простое и наглядное представление направляемых мод в ОВ с помощью лучей не учитывает свойства света как электромагнитной волны и во многих случаях не позволяет получить правильные результаты. Например, в соответствии с изложенным выше вся бесконечная совокупность лучей, падающих на торец ОВ в пределах угла θ_А, должна образовывать также бесконечную совокупность направляемых мод. Однако это не так. Волновая теория света показывает, что только конечное число лучей конического пучка с определенными углами падения на торец может образовать направляемые моды ОВ. Это объясняется с точки зрения лучевой оптики в ступенчатом световоде тем, что при полном внутреннем отражении от границы с оболочкой волна приобретает фазовый сдвиг, зависящий от угла падения. Если в сердцевине многократно отраженные волны складываются по фазе, то образуется направляемая волна. В противном случае поля волн взаимно компенсируются.