1.2. Процессы в ключе на биполярном транзисторе
2.1. Общие сведения о мультивибраторах как релаксационных генераторах
2.3. Методы регулирования длительности импульса
2.4. Автоколебательный мультивибратор
2.5. Регулирование частоты автоколебательного мультивибратора
3. Генераторы линейно изменяющегося напряжения
3.2. Простейший генератор линейно изменяющегося напряжения
3.3. ГЛИН с отрицательной обратной связью
4.2. Перевод чисел из одной системы счисления в другую
4.3. Арифметические операции в двоичной системе счисления
4.4. Формы представления чисел с фиксированной и плавающей точками
5. Логические основы вычислительной техники
5.1. Понятие о логической функции и логическом устройстве
5.2. Элементарные логические функции
5.3. Полные системы функции алгебры логики
6. Комбинационные цифровые устройства
6.6. Одноразрядный двоичный сумматор
1. Электронные ключи
1.1. Общие сведения
Одним из основных элементов импульсной и цифровой техники является ключевое устройство. Ключевые устройства (ключи) служат для коммутации (переключения) цепей нагрузки под воздействием внешних управляющих сигналов. Ключи входят в качестве отдельных элементов в состав сложных устройств - триггеров, мультивибраторов и т. д. Ключ может находиться либо в замкнутом, либо в разомкнутом состоянии. В замкнутом состоянии (ключ включен) сопротивление ключа мало, через него течет большой ток и все напряжение источника выделяется на резисторе R. Напряжение на выходе Uвых равно нулю. В разомкнутом состоянии (ключ выключен) сопротивление ключа бесконечно большое, поэтому ток через него практически не протекает. Напряжение на выходе Uвых равно Е. Следовательно, при коммутации ключа на выходе создаются перепады напряжения с амплитудой Um=E. В зависимости от вида элемента, применяемого для коммутации, ключевые устройства подразделяются на механические, электромеханические и электронные. Примером механического ключа является обычный выключатель. Электромагнитное реле выполняет функции электромеханического ключа, который под воздействием электрического управляющего сигнала производит коммутацию контактов.
Для построения электронных ключей используют диоды, транзисторы, электронные лампы и т. д. В зависимости от того, какой прибор использован, различают диодные, транзисторные, ламповые и т. п. ключи.
При создании транзисторных ключей используются биполярные или полевые транзисторы.
1.2. Процессы в ключе на биполярном транзисторе
Принцип работы ключа
В качестве основного примера рассмотрим транзисторный ключ на кремниевом транзисторе типа п-р-п. Такие ключи являются одним из основных элементов интегральных микросхем, они также могут быть реализованы и на дискретных элементах. Переход к транзисторам типа р-п-р сводится лишь к изменению полярности источников питания (в тех случаях, когда такой переход связан со схемными изменениями, они оговариваются дополнительно). Наибольшее распространение получил транзисторный ключ по схеме с общим эмиттером. Его принципиальная схема приведена на рис. 1. Транзисторный ключ может находиться в одном из двух состояний: ВЫКЛЮЧЕНО, когда транзистор закрыт и ключ разомкнут, и ВКЛЮЧЕНО, в этом случае транзистор открыт и ключ замкнут.
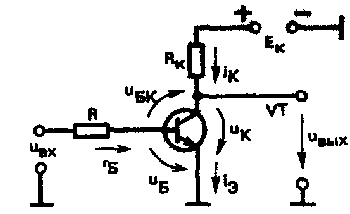
Ключем управляют, подавая на его вход управляющее напряжение Uвых. Включенному состоянию соответствует низкий положительный уровень входного сигнала Uвых=U0. Включенное состояние обеспечивается высоким положительным уровнем входного сигнала Uвых=U1. Ключ удерживается в одном из состояний, пока на входе сохраняется соответствующий уровень сигнала. Резистор R ограничивает ток базы, Rк - коллекторная нагрузка, Ек - источник коллекторного напряжения. Транзистор ключа описывается с помощью семейства входных и выходных характеристик, изображенных на рис.2.
Особенностью входных характеристик кремниевого транзистора является наличие достаточно большого порога отпирания Uп.. При напряжении на базе, меньшем порога отпирания, транзистор всегда закрыт.
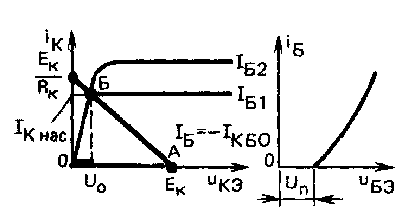
Для анализа работы ключа на семейство выходных характеристик наносят нагрузочную прямую, соответствующую определенному сопротивлению резистора Rк и пересекающую координатные оси в точках Ек и Ек/Rк. При изменении базового тока iб рабочая точка перемещается вдоль этой прямой, определяя в каждый момент времени коллекторный ток , напряжение между коллектором и эмиттером и режим работы транзистора.
Режимы транзистора
В соответствии с функциями ключа транзистор может находиться в одном из двух статических режимов: режиме отсечки (транзистор закрыт) и режиме насыщения (транзистор открыт и насыщен). Активный режим работы обусловлен переходом из одного статического режима в другой.
Режим отсечки (транзистор закрыт). На входе действует напряжение . В этом режиме ток коллектора равен обратному току коллекторного перехода. Напряжение на выходе ключа практически равно напряжению источника питания Uвых=Ек (определяя ивых, необходимо суммировать все напряжения, проходя по внешней цепи от коллектора к эмиттеру).
Рабочая точка находится в точке А на нагрузочной прямой (см. рис. 2). Для обеспечения такого режима в кремниевых транзисторах необходимо выполнить условие: Uп > Uвых=U0 .
Напряжение Uб, приложенное к базе транзистора, определяют, проходя от базы к эмиттеру по внешней цепи (см. рис. 1). Оно равно сумме двух составляющих: падения напряжения на сопротивлении R от тока /КБО ; остаточного напряжения источника входного сигнала Uвых=U0 , которое, как правило, снимается с другого аналогичного ключа и не равно нулю (см. ниже режим насыщения). Оба напряжения имеют одинаковую полярность и стремятся открыть эмиттерный переход.
Таким образом, Uвых=U0 + R * /КБО и условие отсечки для кремниевых транзисторов определяется неравенством: Un > U0 + R * /КБО .
Это условие должно выполняться при максимальной температуре коллекторного перехода, когда напряжение Un минимально, а обратный ток коллектора максимален. Нужно иметь в виду, что ток кремниевых транзисторов достаточно мал.
При выполнении условия отсечки оба перехода транзистора будут закрыты. Коллекторный переход (верхний по схеме) смещен в обратном направлении, так как напряжение на коллекторе равно +Ек. Учитывая это, часто считают, что в режиме отсечки все выводы транзистора разъединены.
Активный режим (транзистор открыт, но не насыщен). Напряжение на входе лежит в пределах Un < Uвых < U1 . В этом режиме транзистор находится короткое время, равное времени переключения из одного статического состояния в другое. Через электроды транзистора протекают прямые токи базы, коллектора и эмиттера. При изменении Uвых меняется ток базы и рабочая точка перемещается по нагрузочной прямой от точки А к точке Б (см. рис. 2). Входной (базовый) и выходной (коллекторный) токи связаны между собой линейно с помощью статического коэффициента передачи тока в схеме с общим эмиттером. Напряжение на выходе равно разности напряжений источника коллекторного питания и падения напряжения на Rк от тока коллектора, протекающего через коллекторный переход:
С увеличением тока базы увеличивается коллекторный ток. Это ведет к увеличению падения напряжения на резисторе Rк, а следовательно, и уменьшению напряжения на коллекторе ик= ивых. При некотором токе базы, называемом током базы в режиме насыщения /Б нас, рабочая точка попадает в точку Б (см. рис. 2), которой соответствует значение коллекторного тока /к нас, называемое током коллектора в режиме насыщения, и транзистор переходит в режим насыщения.
Режим насыщения (транзистор открыт и насыщен). В режиме насыщения на входе действует напряжение Uвых = U1, которое вызывает появление тока, втекающего в базу iб > / Б нас. Этот ток соответствует границе между активным режимом и режимом насыщения (см. точку Б рис. 2). В этой точке тoк базы еще связан линейной зависимостью с током коллектора.
В режиме насыщения транзистор полностью открыт, т. е. оба перехода смещены в прямом направлении, и коллекторный ток ограничивается только резистором Rк. Пренебрегая падением напряжения на открытом транзисторе, можно записать: iк = / К нас = Ек/Rк.
Выходное напряжение ключа Uвых= U0, где U0 - остаточное напряжение на коллекторе открытого транзистора.
Для количественной оценки глубины насыщения часто используют понятие коэффициента насыщения S, который показывает, во сколько раз ток iб , втекающий в базу транзистора, превышает ток базы, при котором транзистор оказывается на границе насыщения.
Поскольку на границе насыщения напряжения между выводами транзистора составляют доли вольта, а дифференциальные сопротивления значительно меньше внешних сопротивлений ключевого устройства, часто считают, что все выводы транзистора в этом режиме замкнуты между собой и транзистор представляет собой точку.
Динамический режим ключа
При анализе работы транзисторного ключа предполагалось, что переход его из состояния ВЫКЛЮЧЕНО в состояние ВКЛЮЧЕНО происходит мгновенно. В действительности, даже если подавать на вход ключа идеальный прямоугольный импульс или перепад, соответствующие изменения выходного напряжения будут происходить не мгновенно, а в конечные промежутки времени, определяемые длительностью переходных процессов.
Инерционные факторы, влияющие на работу ключа. Возникновение переходных процессов объясняется инерционными свойствами, которыми обладают как сам транзистор, так и внешние цепи, подключенные к нему. Инерционность таких цепей связана с наличием паразитных емкостей (монтажа, нагрузки и т. д.), которые при переключении ключа заряжаются и разряжаются за конечное время. Учтем эту емкость введением в схему ключа некоторой нагружающей емкости Сн (рис. 3).
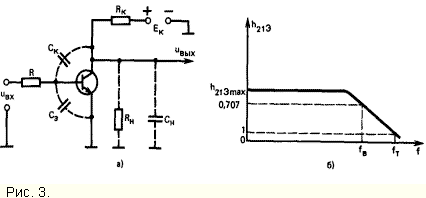
Инерционность транзистора, обусловленная процессами накопления и рекомбинации заряда в базе при коммутации ключа, называется внутренней, а инерционность транзистора, вызванная наличием барьерных емкостей переходов, называется внешней.
Внутренняя инерционность транзистора учитывается введением некоторой постоянной времени r. С параметром r связаны процессы накопления и рекомбинации заряда в базе, определяющие механизм действия транзистора. Вспомним физическую сущность параметра r. В процессе работы транзистора под действием тока в базе накапливается заряд. Если базовый ток прекращается, то заряд, накопленный в базе, будет убывать по экспоненциальному закону благодаря рекомбинации зарядов. Время, в течение которого число неосновных носителей в базе уменьшается в е раз (где е-основание натурального логарифма), обозначается постоянной времени r. Постоянная времени r определяет внутренние инерционные свойства транзистора в схеме с общим эмиттером и называется временем жизни неосновных носителей в базе. Время жизни неосновных носителей в базе может меняться в зависимости от режима работы и типа транзистора. Так, при работе дрейфовых транзисторов в режиме насыщения постоянная времени, обозначаемая Тнас, увеличится, Тнас=(2-6)*r . Для бездрейфовых транзисторов можно считать, что Тнас>>р .
Внутренняя инерционность - общее свойство транзистора - проявляется не только в ключевом, но и в усилительном режиме работы транзистора. В усилительном режиме наличие внутренних инерционных свойств приводит к тому, что динамический коэффициент передачи по току зависит от частоты. Так как на практике эту зависимость легко измерить, то параметр r определяют, пользуясь этой зависимостью.
Время жизни носителей оказывается обратно пропорциональным частоте, на которой коэффициент передачи равен 1.
Следует иметь в виду, что такую же зависимость коэффициентa передачи от частоты имеет не только транзистор, но и интегрирующая цепь. Поэтому упрощенно можно полагать, что переходные процессы, возникающие вследствие внутренней инерционности транзистора, описываются дифференциальным уравнением первого порядка с постоянной времени r. В этом случае для расчетов применимо общее соотношение, являющееся решением дифференциального уравнения первого порядка с постоянной правой частью.
Барьерные емкости Су и Ск, являющиеся причиной внешней инерционности транзистора, нелинейны и зависят от приложенных к переходам напряжений. Усреднив их по всему диапазону, напряжения Сэ и Ск можно отнести к внешней схеме ключа, как постоянные. Поэтому Сэ и Ск и называют внешними инерционными параметрами транзистора.
При работе транзистора в активном режиме возникает обратная связь с коллектора на базу транзистора через емкость коллекторного перехода Ск, что также является причиной внешней инерционности транзистора. Внешнюю инерционность из-за действия обратной связи через Ск учитывают, вводя постоянную времени rк Общая постоянная времени транзистора в схеме ключа для активного режима равна сумме постоянных времени, обусловленных внутренними и внешними инерционными факторами транзистора.
Описание переходных процессов
Рассмотрим переходные процессы, происходящие в ключе при подаче на его вход прямоугольного импульса. Временные диаграммы, иллюстрирующие изменение тока базы iб(t), заряда Q(t),.тока коллектора Iк(t) и т. д. изображены на рис. 4.
Исходное состояние. В исходном состоянии транзистор находится в режиме отсечки, поскольку напряжение на входе Uвх= U0 меньше порога отпирания. Рабочая точка на семействе выходных характеристик и на передаточной характеристике находится в точке А (см. рис. 1.14, 1.17).
Включение. В момент t=t1 на вход ключа подается положительный импульс, амплитуда которого больше порогового значения. Этот импульс вызывает появление в цепи базы перепада тока. Ток базы во время действия входного импульса можно считать практически неизменным, так как входное сопротивление транзистора обычно много меньше сопротивления R. Под воздействием входного перепада тока транзистор переходит последовательно из области отсечки в активную область и далее в область насыщения.
Процесс включения транзисторного ключа обычно подразделяют на два этапа: задержка включения (или подготовка включения) и формирование фронта выходного импульса.
Задержка включения. Интервал времени t1-t2 от момента подачи входного импульса до начала нарастания коллекторного тока, определяет время задержки включения tЗ. Транзистор в это время находится в режиме отсечки.
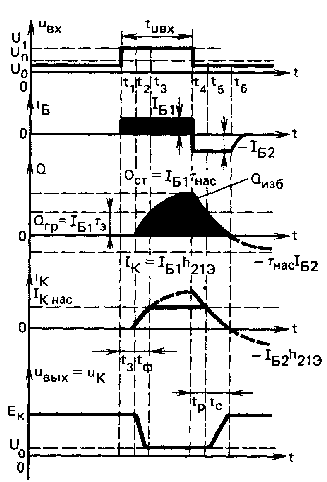
Возникновение задержки при включении ключа объясняется зарядом барьерных емкостей Сэ и Ск током БАЗЫ. В процессе заряда напряжение на емкостях Сэ и Ск под действием входного импульса нарастает от значения U0, стремясь к U1. В тот момент, когда напряжение на базе достигает порогового значения Un, эмиттерный переход открывается и транзистор переходит из режима отсечки в активный режим.
Рабочая точка на нагрузочной прямой за время задержки не меняет своего положения.
Заряд барьерных емкостей происходит в цепи первого порядка с постоянной времени rЗ=R(Ск+Сэ). Практически время задержки весьма мало, поэтому им часто пренебрегают.
Формирование фронта происходит в интервале t2-t3 . В момент времени t2 напряжение на базе становится равным пороговому, транзистор открывается и переходит в активный режим. Начинается накопление заряда неосновных носителей, инжектированных в базу. По мере увеличения заряда увеличивается ток коллектора, который пропорционален Q(t), и уменьшается напряжение на коллекторном переходе. Скорость накопления заряда в базе определяет скорость нарастания коллекторного тока.
В момент t3, когда заряд достигает граничного значения коллекторный переход смещается в прямом направлении и транзистор переходит в состояние насыщения. Рост коллекторного тока прекращается, поскольку он оказывается ограниченным параметрами внешней цепи:
За время формирования фронта рабочая точка по нагрузочной прямой перемещается из точки А в точку Б (см. рис. 2). Интервал времени t2-t3, в течение которого коллекторный ток меняется от 0 до /К нас, называется длительностью фронта. Транзистор в это время находится в активном режиме.
Накопление избыточного заряда. После окончания формирования фронта в момент времени t3 транзистор переходит в режим насыщения. Коллекторный переход смещается в прямом направлении. Коллекторный ток практически постоянен и равен / К нас . Однако заряд в базе продолжает нарастать, стремясь к стационарному значению, определяемому входным током.
Избыточный заряд возникает только в том случае, если ток базы превышает значение /Б нас. В режиме насыщения нарушается пропорциональность между током базы и током коллектора. Коллекторный ток уже не может следовать за базовым, так как он ограничен сопротивлением Rк- В противном случае закон изменения коллекторного тока повторял бы закон изменения заряда Q(t), вызываемое током базы. Необходимо отметить, что при переходе транзистора в режим насыщения изменяется время жизни неосновных носителей в базе, которое для области насыщения обозначается символом Тнас и называется постоянной времени транзистора в области насыщения. Постоянная времени Тнас определяет как процесс накопления, так и стационарный уровень заряда в базе. Стационарного значения заряд достигает за время, не меньшее, чем 2,3* Тнас после начала накопления. Если длительность входного импульса меньше этого значения, то заряд в базе к концу будет меньше Qст.
В режиме насыщения рабочая точка на нагрузочной прямой остается в точке Б, а на передаточной характеристике перемещается из точки Д в точку Б.
Выключение. В момент времени t4 действие входного отпирающего импульса заканчивается. Возникает обратный ток базы. Под воздействием процесса рекомбинации заряд неосновных носителей в базе уменьшается. Спустя некоторое время транзистор выходит из насыщения и переходит в активную область, а затем запирается.
Процесс выключения можно разделить на два этапа: рассасывание избыточного заряда и формирование спада импульса.
Рассасывание избыточного заряда. Происходит в течение интервала времени t4-t5. Этот процесс является причиной возникновения задержки при выключении ключа. Заряд неосновных носителей в базе мгновенно измениться не может, поэтому требуется время, чтобы он уменьшился от стационарного значения в режиме насыщения Qст до граничного значения. В течение этого времени транзистор остается в режиме насыщения, ток коллектора постоянен и равен /Кнас, а Uк_=Uк нас=Uo.
Время, в течение которого транзистор продолжает оставаться в режиме насыщения после окончания входного импульса, называется временем рассасывания.
К концу процесса рассасывания рабочая точка на передаточной характеристике перемещается в точку Д, а положение рабочей точки на нагрузочной прямой не меняется.
Формирование среза импульса. Начинается в момент времени t5,, когда избыточный заряд уменьшается до нуля. Коллекторный переход смещается в обратном направлении, и транзистор из режима насыщения переходит в активный режим. В течение интервала t5-t6, называемого длительностью среза, заряд в базе продолжает убывать, уменьшаясь от Qrp до нуля, рабочая точка как на нагрузочной прямой, так и на передаточной характеристике возвращается в точку А. Коллекторный ток в активном режиме пропорционален заряду и изменяется от /Кнас, стремясь по экспоненциальному закону к 0. В момент t6 транзистор запирается и /к=0.
Далее в течение некоторого времени t6,-t7 происходит изменение заряда барьерных емкостей переходов Сэ и Ск. За время этого процесса ток базы уменьшается до нуля, а на базе устанавливается исходное напряжение Uo.
1.3. Влияние изменения параметров схемы ключа на его работу
Значения элементов и напряжений в схеме транзисторного ключа влияют на длительности соответствующих процессов.
Изменение параметров коллекторной цепи Rк и Ек приводит к изменению тока /к нас и влияет на длительности всех трех процессов. Например, уменьшение Ек до Е'к ведет к уменьшению /К нас до /'К нас. При включении ключа амплитуда коллекторного тока будет нарастать до меньшего значения /К нас в цепи с неизменной постоянной времени; это приведет к уменьшению длительности фронта. При уменьшении
/K нас транзистор выходит на границу насыщения при меньшем токе базы, поэтому все дальнейшее увеличение тока базы вызывает накопление избыточного заряда, что ведет к увеличению времени рассасывания.
Спадать коллекторный ток начнет с меньшего значения, поэтому время среза уменьшится. Уменьшение /К нас из-за увеличения Rк влияет на изменение времен двояко. С одной стороны, при уменьшении /К нас уменьшаются длительности фронта и среза и увеличивается время рассасывания. Но, с другой стороны, особенно при использовании дрейфовых транзисторов, увеличивается постоянная времени транзистора в активном режиме вследствие увеличения слагаемого, обусловленного внешним инерционным фактором. Это увеличение приводит к увеличению tc, поэтому изменением Rк можно изменять потребляемую мощность и пропорционально ей изменять быстродействие при условии, что длительность рассасывания сравнительно мала.
Прямой ток включения базы /Б можно увеличить, повысив напряжение Uвх. При этом длительность фронта уменьшается из-за увеличения скорости нарастания тока, а длительность рассасывания увеличивается вследствие накопления избыточного заряда. Длительность среза остается неизменной. При изменении сопротивления R, например уменьшении, происходит пропорциональное увеличение тока базы, процесс включения протекает быстрее. Сокращается и процесс выключения, поскольку ток /К спадает от /К нас до нуля с большей скоростью, стремясь к более низкому уровню. Время рассасывания увеличивается.
Рассмотренные примеры показывают, что изменение режимов работы транзистора, работающего по схеме ключа, не позволяет заметно повысить его быстродействие, поскольку при неизменной потребляемой мощности уменьшение длительности одних процессов сопровождается увеличением длительности других. Для повышения быстродействия используют более сложные схемы ключей.
1.4. Схемы ключей с повышенным быстродействием
Как следует из рассмотренного выше, быстродействие ключа можно увеличить, переключив его током базы, временная диаграмма которого представляет на рис. 5,а. В момент t1 для ускорения процесса ключ включается большим током /Б1, затем в момент времени t2 ток уменьшается до значения /'Б1, т. е. транзистор выводится на границу режима насыщения для уменьшения длительности рассасывания. В момент t3 транзистор запирается большим базовым током /Б2.
Ключ с форсирующей (ускоряющей) емкостью. Форму тока, близкую к оптимальной, можно получить, шунтировав резистор R конденсатором (рис. 1.23,6). При появлении входного напряжения в момент t1 транзистор начинает открываться. Базовый ток транзистора в первый момент замыкается через конденсатор, так как последний представляет собой малое сопротивление, близкое к короткому замыканию для скачка тока. Вследствие этого в момент /1 базовый ток имеет большое значение:
/Б1 =( Uвх - Uбэ ) / RИ
где Ru - внутреннее сопротивление источника сигнала (например, выходное сопротивление предыдущего ключа); обычно Ru >> R.

Этот ток быстро заряжает барьерные емкости и накапливает заряд в базе транзистора. Благодаря большому току уменьшаются длительности задержки и фронта. По мере заряда конденсатора ток базы уменьшается до значения /'Б1 = Uвх / R , определяемого сопротивлением R, которое выбирается из условия насыщения. Благодаря этому к моменту окончания входного импульса в базе накапливается сравнительно небольшой избыточный заряд.
В момент t3 окончания входного сигнала конденсатор С разряжается через базу транзистора, создавая большой запирающий ток базы /Б2 = Uc / Ru .
Этот ток ускоряет процессы рассасывания и выключения транзистора.
Емкость С не должна быть слишком малой, иначе длительность всплесков токов будет меньше, чем длительность процессов переключения, которую они уменьшают. При этом процесс переключения будет протекать в основном при сравнительно малых токах базы, т. е. не будет ускоряться.
Нельзя выбирать ускоряющий конденсатор и слишком большой емкости, поскольку в этом случае: во-первых, ток базы не успеет уменьшиться до уровня /Б2 к концу входного импульса и в базе накопится весьма большой избыточный заряд; во-вторых, конденсатор не будет успевать заряжаться до уровня входного импульса к моменту его окончания, процессы рассасывания и включения будут протекать медленнее.
Ключ с нелинейной обратной связью. Обеспечить большой базовый ток включения и одновременно уменьшить время рассасывания можно, используя схему ключа с отрицательной обратной связью, в которой не допускается насыщенный режим работы транзистора. Особенно важно это при использовании высокочастотных дрейфовых транзисторов, отличающихся тем, что у них время жизни неосновных носителей в режиме насыщения значительно больше, чем в активном режиме. Схема ненасыщенного ключа приведена на рис. 6.
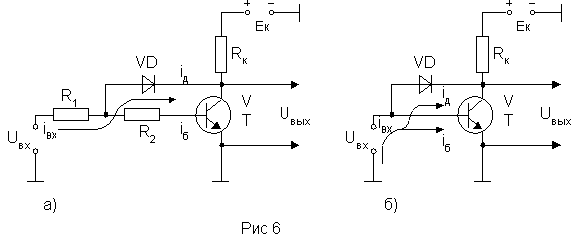
Нелинейная отрицательная обратная связь осуществляется через диод VD. Состояние диода определяется полярностью и величиной напряжения, действующим между анодом и катодом диода. В исходном состоянии диод закрыт за счет высокого положительного потенциала на катоде. Отрицательная обратная связь не действует. При подаче большого входного сигнала Uвх = U1, входной ток вначале течет через R1 и R2 в базу транзистора, обеспечивая большой ток включения /Б1. В процессе отпирания транзистора напряжение на коллекторе уменьшается от Ек, стремясь к 0, и в тот момент, когда напряжение между базой и коллектором уменьшаясь достигнет значения, равного падению напряжения от входного тока на R2, диод VD открывается и часть входного тока будет протекать через диод и коллектор на землю в обход базы. В результате ток базы уменьшается до значения /'Б1 <= /'Б нас, и транзистор не входит в насыщение. Сопротивление R2 выбирают таким, чтобы падение напряжения на нем за счет тока базы было больше падения напряжения на открытом диоде. В этом случае напряжение между коллектором и базой остается положительным, хотя и небольшой величины, и вхождение транзистора в насыщение предотвращается.
При изготовлении ключа методами микроэлектроники в цепи обратной связи иногда используются диоды Шотки, выполненные в едином технологическом процессе с интегральным транзистором также с барьером Шотки. Диод Шотки представляет собой переход металл - полупроводник.
Для работы ключа с нелинейной обратной связью необходимо, чтобы диод, включенный параллельно коллекторному переходу транзистора, открывался при сравнительно малом напряжении, когда коллекторный переход еще закрыт. Это и обеспечивает диод с барьером Шотки.
В подобных ключах можно получить очень малые времена выключения, поскольку транзисторы с барьером Шотки имеют, как правило, более высокие значения коэффициента усиления и более низкие значения неуправляемых токов.
2. Мультивибраторы
2.1. Общие сведения о мультивибраторах как релаксационных генераторах
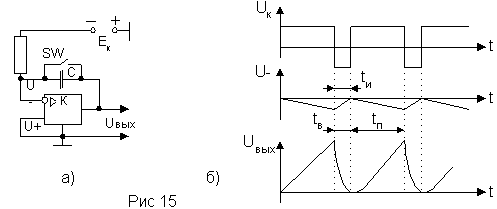
Мультивибратор относится к релаксационным генераторам. Релаксационный генератор является источником колебаний, форма которых отличается от синусоидальной. Релаксационные колебания бывают прямоугольные, пилообразные и т. д. Генераторы релаксационных колебаний используют для формирования одиночных импульсов и импульсных последовательностей, деления частоты, в качестве запускающих элементов, источников синхронизирующего сигнала и т. д.
Колебательный процесс в релаксационном генераторе состоит в поочередном накоплении энергии от источника питания накопителем и выделении ее в виде тепла в резисторах схемы. Накопитель переключается с процесса накопления на выделение энергии с помощью коммутирующего устройства при достижении определенного уровня энергии. Управление коммутирующим устройством производится по цепи обратной связи. Таким образом, релаксационный генератор обязательно содержит источник энергии, накопитель, коммутирующее устройство и цепь обратной связи. В качестве коммутирующего устройства обычно используют транзистор, работающий в ключевом режиме.
Релаксационный генератор может работать в одном из следующих режимов: ждущем, автоколебательном, синхронизации и деления частоты.
В ждущем режиме генератор имеет состояние устойчивого и квазиустойчивого равновесия. Квазиустойчивым равновесием называют такое состояние генератора, при котором он, будучи выведенным из состояния равновесия, через некоторое время возвращается к этому состоянию благодаря внутренним процессам. Переход из устойчивого равновесия в квазиустойчивое происходит под действием запускающих импульсов, а обратно генератор возвращается самопроизвольно через время, зависящее от параметров генератора.
В автоколебательном режиме состояния устойчивого равновесия нет, а существует два состояния квазиустойчивого равновесия. В процессе работы генератор переходит из одного квазиустойчивого состояния в другое. Период колебаний определяется параметрами генератора.
В режиме синхронизации на релаксационный генератор действует внешнее синхронизирующее напряжение. Генератор имеет также два квазиустойчивых состояния, однако период колебаний определяется синхронизирующим сигналом.
Среди большого числа разнообразных релаксационных генераторов можно выделить два типа в зависимости от способа организации обратной связи: мультивибраторы и блокинг-генераторы. Подобные генераторы широко применяются в импульсной технике. Мультивибратор представляет собой двухкаскадное устройство, обратная связь в котором образуется соединением выхода одного каскада со входом другого и, наоборот, с помощью конденсаторов. Блокинг-генератор - это устройство, обратная связь с выхода на вход которого осуществляется через импульсный трансформатор. Обратная связь в этих устройствах положительная.
2.2. Ждущий мультивибратор
Схема и принцип действия. Ждущий мультивибратор (иногда его называют одновибратором) предназначен для формирования одиночных импульсов заданной длительности. Форма импульсов близка к прямоугольной. Формирование импульса на выходе одновибратора происходит только после подачи на вход запускающего сигнала. До подачи запускающего сигнала мультивибратор находится в устойчивом состоянии, т. е. как бы ждет запуска, поэтому такой режим называют ждущим.
После подачи запускающего сигнала осуществляется переход в следующее состояние, называемое квазиустойчивым, так как в нем мультивибратор долго находиться не может, и через некоторое время самостоятельно возвращается к устойчивому состоянию.
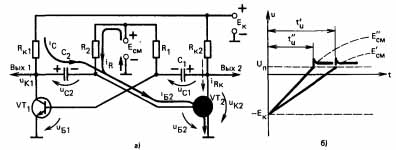
Принципиальная схема одновибратора с коллекторно-базовыми связями приведена на рис. 7,а. Схема содержит два каскада. Один из них, собранный на транзисторе VT1, представляет собой транзисторный ключ с форсирующей емкостью; R1 и C1 - элементы базовой, а Rк1 - коллекторной цепи этого каскада. Второй каскад, собранный на транзисторе VT2, служит усилителем с резистивно-емкостной (R2,C2) связью. Вход (базовая цепь) каждого из каскадов подключен к выходу (к коллектору) другого каскада. Такое включение каскадов в мультивибраторе создает петлю положительной обратной связи.
На базу транзистора VT2 через резистор R2 подается напряжение от источника Ек - положительной полярности. Выходной сигнал снимается с коллектора транзистора VT2. Элементы Сз, Rз, представляющие собой укорачивающую цепочку, совместно с диодом VD образуют цепь запуска.
Работа мультивибратора в ждущем режиме может быть разделена на три этапа: исходное состояние, рабочий период и период восстановления. Процессы, происходящие в мультивибраторе, иллюстрируют диаграммы на рис. 7,б.
Исходное устойчивое состояние. Транзистор VT2 открыт, a VT1 закрыт. Транзистор VT2, удерживается в открытом состоянии током IБ2, создаваемым источником Ек и втекающим в базу транзистора VT2 через резистор R2. Этот ток равен: /Б2 = (Ек- UБЭ НАС 2) / R2. Сопротивление R2 выбрано таким, чтобы ток базы транзистора VT2 был больше тока базы на границе насыщения. Поэтому транзистор VT2 насыщен. Напряжение на его коллекторе UК2 имеет небольшое остаточное значение.
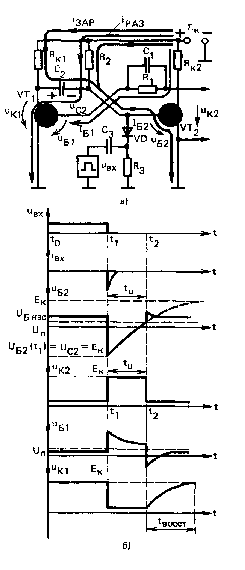
При открытом и насыщенном транзисторе VT2 транзистор VT1 будет закрыт, если напряжение на его базе UБ 2 меньше порога открывания Un, т. е. UБ 2 < Un.
Напряжение UБ 1, приложенное к базе VT1 складывается из остаточного напряжения UКЭнас2 на коллекторе насыщенного транзистора VT2 и падения напряжения на R1 от тока /КБ0 транзистора VT1. Напряжение определяют алгебраическим суммированием напряжений на элементах при обходе замкнутого контура от базы транзистора VT1 к его эмиттеру. Таким образом, VT1 закрыт, если выполняется условие: UБ1 < UП.
Это условие обеспечивают, подбирая параметры схемы ждущего мультивибратора.
Напряжение на коллекторе закрытого транзистора VT1 близко к ЕК. Конденсатор С2 заряжен до напряжения UC2 =ЕК - UБЭ НАС 2 (это напряжение определяется суммированием напряжений между коллектором и эмиттером и эмиттером и базой VТ2, т. е. на элементах внешнего по отношению к конденсатору контура при обходе его в направлении от левой обкладки к правой). Конденсатор C1 практически разряжен.
Запуск и опрокидывание. В момент t1 на базу VT2 поступает импульс тока, формируемый цепью запуска. Под действием этого импульса транзистор VT2 закрывается, напряжение UК 2 на его коллекторе нарастает до значения, близкого к Ек. Поскольку это напряжение существенно превышает порог открывания Un транзистора VT1, последний открывается и входит в насыщение, что обеспечивается соответствующим выбором сопротивления R1. Таким образом, под действием импульса запуска VT1 открылся, а VT2 закрылся, т. е. произошло опрокидывание ждущего мультивибратора.
Короткие импульсы, необходимые для запуска, либо подаются на вход ждущего мультивибратора непосредственно от источника запускающих сигналов либо формируются с помощью цепи запуска из перепадов напряжения, подаваемого на вход устройства. Принцип действия цепи поясняют временные диаграммы, представленные на рис. 7,б.
Конденсатор С3 заряжается под действием высокого напряжения, подаваемого на вход в момент t=0. Поскольку диод VD в это время закрыт, положительный импульс, сформированный цепью R3, С3 в базу транзистора VT2 не проходит, а замыкается через резистор R3. В момент t=t1, когда на входе действует отрицательный перепад напряжения, конденсатор С3 разряжается через открытый диод VD и входную цепь транзистора VT2, так как сопротивление резистора R3 выбирается много больше суммы сопротивлений открытого диода и входного сопротивления открытого транзистора. При этом образуется импульс обратного базового тока, обеспечивающий быстрое закрывание VT2. Дальнейший временной ход процессов в устройстве поясняют диаграммы, приведенные также на рис. 7,б. Итак, в момент t1 под действием входного токового импульса транзистор VT2 закрывается.
Квазиустойчивое состояние. После отпирания VT1 в момент t1 к эмиттерному переходу VT2 прикладывается обратное напряжение UБ 2 = UКЭ НАС 1 - UС2 (напряжение между базой и эмиттером транзистора VT2 определяется суммированием напряжений вдоль внешнего по отношению к VT2 контура при обходе его от базы к эмиттеру).
Остаточное напряжение UКЭ НАС 1 на коллекторе насыщенного транзистора мало по сравнению с UС2, поэтому, пренебрегая им, считают, что все напряжение UС2 через открытый транзистор VT1 прикладывается к базе VT2, т. е. UБ 2 = - UС2. Это напряжение удерживает транзистор VT2 в закрытом состоянии и после окончания импульса запуска. Ждущий мультивибратор в течение этого времени находится в квазиустойчивом состоянии.
В этом состоянии конденсатор С2 перезаряжается частью коллекторного тока транзистора VT1, протекающего по цепи: конденсатор С2, резистор R2, источник Ек. В процессе перезаряда напряжение на конденсаторе изменяется от значения UС2 = - EK, стремясь к величине UС2 = EK. В соответствии с изменением напряжения на конденсаторе меняется и напряжение UБ 2 на базе транзистора VT2. В момент времени t=t2 напряжение на перезаряжающемся конденсаторе С2 достигает порогового значения. Так как это напряжение приложено к базе VT2, то транзистор VT2 открывается и на его коллекторе вновь устанавливается низкое напряжение UКЭ НАС 2. Вследствие этого транзистор VT1 закрывается. Конденсатор C1 ускоряет процессы открывания и закрывания транзистора VT1 так же, как это происходит в транзисторном ключе с форсирующей емкостью. Таким образом, в момент t2 происходит обратное опрокидывание ждущего мультивибратора, и устройство возвращается в устойчивое состояние. На выходе (на коллекторе VT2) возникает импульс, длительность которого равна времени пребывания ждущего мультивибратора в квазиустойчивом состоянии, которое определяется временем перезаряда конденсатора С2 от напряжения Ек - UБЭ НАС 2 до напряжения Uп.
Восстановление. После возвращения в момент t2 устройства в устойчивое состояние начинается процесс восстановления, в ходе которого устанавливаются напряжения, соответствующие исходному состоянию. Часть базового тока транзистора VT2, замыкаясь по цепи конденсатор С2, резистор Rк1 источник Ек, заряжает конденсатор С2. По мере роста напряжения UС2 уменьшаются зарядный ток, падение напряжения на резисторе Rк1 и напряжение UК1 приближается к установившемуся значению Ек.
Следующий запуск устройства можно производить после того, как UК 1 = UС 2 приблизится к Ек с высокой точностью. В противном случае, если UС 2 окажется к моменту запуска существенно меньше Ек, то напряжение на базе транзистора VT2 будет снижаться с меньшего значения и, следовательно, раньше достигает нуля, раньше откроется транзистор, так как уменьшится длительность импульса tu.
Проведенный анализ процессов, происходящих в ждущем мультивибраторе, позволяет сделать вывод о том, что он имеет все необходимые элементы релаксационного генератора: конденсатор С2 выполняет роль накопителя энергии, которая рассеивается затем в результате разряда конденсатора; транзистор VT1, управляемый по цепи обратной связи, переключает С2 с заряда на разряд, т. е. служит коммутатором.
Длительность формируемого импульса равна времени, в течение которого напряжение на базе закрытого транзистора VT2 изменяется от исходного значения Eк в момент t1 до значения Un в момент t2 вследствие перезаряда конденсатора С2. Для инженерных расчетов принимают, что длительность выходного импульса равна: tИ <= 0,7* R2* C2
Температурная нестабильность длительности импульса определяется в основном температурной нестабильностью входной характеристики транзистора и зависимостью /КЭ0 ОТ температуры.
При увеличении температуры входная характеристика кремниевого транзистора смещается влево примерно на 2 мВ/ t °С. Это ведет к уменьшению Un, а значит, и длительности импульса. С другой стороны, ток /КБ0 составляет часть разрядного тока конденсатора. С ростом температуры этот ток растет, что ведет к увеличению разрядного тока конденсатора. При этом напряжение на базе VT2 увеличивается с большей скоростью и раньше достигает Un. В результате длительность импульса также уменьшается. Поскольку основная составляющая тока разряда конденсатора замыкается через резистор R2, то с уменьшением сопротивления уменьшается доля тока /КБ0 в общем разрядном токе, в этом случае влияние нестабильности тока /КБ0 на длительность импульса будет меньше.
Время восстановления обусловлено процессом заряда конденсатора С2, который начинается вслед за обратным опрокидыванием. Заряд конденсатора осуществляется током от источника Ек, протекающим через резистор RК1, и происходит по экспоненциальному закону с постоянной времени раной RК1 * С2. По такому же закону изменяется напряжение на коллекторе первого транзистора от начального значения UКЭ НАС до значения, близкого к Ек.
Следующий запуск можно производить после того, как UС2 приблизится к установившемуся значению Ек - UБЭ НАС 2 с высокой точностью. В противном случае напряжение на базе транзистора VT2 будет нарастать с меньшего значения и, следовательно, раньше достигнет значения Un и откроется раньше VT2, т. е. уменьшится длительность tu формируемого импульса. Время восстановления принимают равным значению : tВОСС = (4…5) * RК1 * С2 .
Период следования импульсов запуска ждущего мультивибратора должен удовлетворять условию TЗАП > tИ + tВОСС .
Амплитуда выходного импульса равна разности уровней напряжения на коллекторе транзистора VT2 в закрытом и открытом состоянии. Когда транзистор VT2 открыт, UК 2 = UК 2 НАС. В закрытом состоянии через R2 протекает ток базы насыщенного транзистора. Тогда в отсутствие нагрузки амплитуда выходного импульса: UM = Ек .
2.3. Методы регулирования длительности импульса
Регулировать tИ можно изменением постоянной времени R2 * C2. Для этого надо изменять емкость С2 или сопротивление R2. Объясним это. С увеличением постоянной времени уменьшается скорость, с которой изменяется напряжение на базе VT2 в течение рабочего состояния. Напряжение UБ 2 позже достигает порогового значения Un, и длительность импульса возрастает. Этот метод можно применять при небольших пределах изменения tu, так как при увеличении R2 транзистор VT2 может выйти из насыщения, а при сильном уменьшении R2, наоборот, может войти в глубокое насыщение, и режим работы одновибратора нарушится. Кроме этого, увеличение R2 ведет к росту температурной нестабильности, а увеличение емкости конденсатора С2 приводит к возрастанию времени восстановления. Другой способ регулировки состоит в изменении начального напряжения на конденсаторе времязадающей цепи. Данный способ регулировки показан на рис. 8. Регулирующее напряжение Up на конденсаторе С2 подают через диод VD, причем Up < Eк. В исходном состоянии диод VD открыт напряжением Ек и потенциал на коллекторе закрытого транзистора фиксируется на уровне Up. Разность Ек-Up падает на резисторе RК2 из-за протекания через него тока открытого диода. Конденсатор С2 оказывается заряженным до напряжения Uc2= Up - UБЭ НАС 2. Таким образом, после запуска мультивибратора напряжение на базе закрытого транзистора VT2 будет изменяться от значения Up - UБЭ НАС 2 , стремясь к Ек. (рис. 8,б). Чем меньше Up, тем раньше напряжение UБ 2 достигнет порогового значения Un и тем меньше длительность выходного импульса.
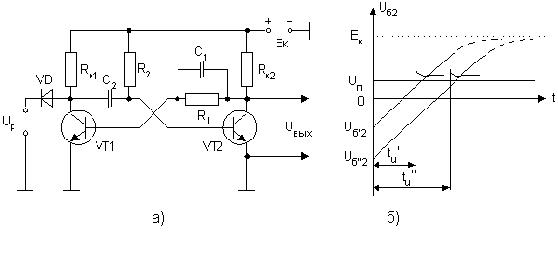
Наряду с регулированием длительности выходного импульса в мультивибраторе (рис. 8,а) уменьшается длительность восстановления. Это явление поясняют временные диаграммы, приведенные на рис. 8,б. После обратного опрокидывания устройства конденсатор С2 заряжается и напряжение на коллекторе транзистора VT1 растет, стремясь к Ек. Однако в тот момент, когда UК1 достигает значения, примерно равного Up, открывается диод и процесс восстановления заканчивается.
2.4. Автоколебательный мультивибратор
Схема и принцип действия. На рис. 9 представлена схема автоколебательного мультивибратора. Мультивибратор состоит из двух каскадов на транзисторах VT1 и VT2. Причем вход каждого каскада (база) подключен через конденсатор к выходу другого (к коллектору). Такое включение обеспечивает наличие петли положительной обратной связи в то время, когда оба транзистора работают в активном режиме. Мультивибратор имеет все элементы, присущие релаксационному генератору: конденсаторы C1 и С2 являются накопителями энергии, транзисторы VT1 и VT2 выполняют роль коммутирующих устройств. Резисторы R1, R2 входят в цепи разряда конденсаторов.
Первое квазиустойчивое состояние. Будем считать, что к моменту t1 мультивибратор перешел в очередное квазиустойчивое состояние, при этом VT1 закрылся, а VT2 открылся и вошел в насыщение. К этому моменту напряжение UС1 на конденсаторе C1 имело максимальное значение, равное Ек - UБЭ НАС 1 (конденсатор C1 заряжен, а конденсатор С2 разряжен).
К базе транзистора VT1i через открытый VT2 прикладывается напряжение UБ1 = - UС1 (напряжение UБ1 между базой и эмиттером транзистора VT1 определяется суммированием напряжения вдоль внешнего по отношению к транзистору контура при обходе его от базы к эмиттеру).
Таким образом, транзистор VT1 удерживается в закрытом состоянии под действием отрицательного напряжения с конденсатора C1, приложенного к базе. Транзистор VT2 остается открытым, поскольку в его базу поступает ток IБ2 = IR2 + IC2, где IR2-составляющая базового тока, протекающая через резистор R2, IC2 - составляющая базового тока, протекающая через RК1 и С2. С момента t1 начинаются два процесса - разряд C1 и заряд C2.
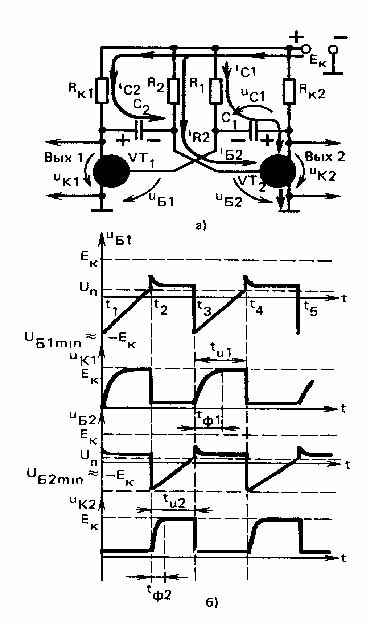
Разряд C1 в автоколебательном мультивибраторе аналогичен соответствующему процессу в квазиустойчивом состоянии ждущего мультивибратора.
Разряд конденсатора C1 осуществляется током IC1, протекающим в цепи: положительный полюс источника Ек, резистор R1, конденсатор C1, открытый переход коллектор-эмиттер транзистора VT2, земля, отрицательный полюс источника Ек. Под действием этого тока, являющегося частью коллекторного тока транзистора VT2, конденсатор С2 стремится не просто разрядиться, а перезарядиться до напряжения, близкого к Ек, но противоположной полярности. При этом напряжение на базе транзистора VT1, меняющееся так же, как и напряжение на C1, нарастает по экспоненте с постоянной времени R1 * C1 от минимального значения стремясь к значению Ек. В момент t2, когда напряжение UБ 1 достигает порогового значения, транзистор VT1 открывается. Отрицательное напряжение с зарядившегося конденсатора C2, примерно равное -Ек, через открытый VT1 прикладывается к базе VT2, вследствие чего VT2 закрывается и мультивибратор переходит в новое квазиустойчивое состояние.
Процесс заряда конденсатора С2, аналогичный процессу восстановления в ждущем мультивибраторе, осуществляется под действием составляющей базового тока IС 2. Составляющая IС 2 протекает в цепи: положительный полюс источника Ек, резистор RК1, конденсатор С2, открытый переход база - эмиттер транзистора VT2, земля, отрицательный полюс источника Ек и заряжает конденсатор С2. Напряжение на нем растет по экспоненте с постоянной времени RК1 * С2, стремясь к Ек. По такому же закону уменьшается ток заряда и создаваемое им напряжение на резисторе RК1. При этом напряжение UК1 растет, стремясь к Ек. После окончания заряда конденсатора С2, когда IC2 = 0, транзистор VT2 продолжает оставаться открытым благодаря току, протекающему через R2. Процесс заряда конденсатора С2 определяет длительность фронта TФ1 выходного импульса, формируемого на коллекторе транзистора VT1. Поскольку сопротивление резистора RК2 всегда бывает меньше сопротивления резистора R1, то заряд конденсатора С2 заканчивается раньше разряда C1 и время нахождения мультивибратора в квазиустойчивом состоянии определяется разрядом C1.
Второе квазиустойчивое состояние. В новом квазиустойчивом состоянии в мультивибраторе происходят процессы, аналогичные описанным выше, только в другой его части. Теперь разряжается конденсатор С2 частью коллекторного тока транзистора VT1, протекающего по цепи +Ек, R2, C2, VT1, -Ек. При этом напряжение на базе транзистора VT2 изменяется по экспоненте с постоянной времени R2 * С2 (рис. 9,б). В момент t3, когда напряжение UБ 2 достигнет значения Uп, вновь открывается транзистор VT2 и мультивибратор возвращается в первое квазиустойчивое состояние. В это же время заряжается конденсатор С1, частью базового тока транзистора VT1, протекающего по цепи C1, RK2, Ек, VT1. Таким образом, автоколебательный мультивибратор периодически переходит из одного квазиустойчивого состояния в другое.
Как видно из временных диаграмм на рис. 9,б, напряжение на коллекторах транзисторов представляет собой последовательность импульсов положительной полярности, форма которых близка к прямоугольной.
Параметры формируемой импульсной последовательности. Рассмотрим основные параметры импульсной последовательности, формируемой мультивибратором.
Процессы, определяющие длительность импульса в каждом квазиустойчивом состоянии мультивибратора, того же характера, что и в ждущем мультивибраторе. Поэтому выражения, описывающие основные параметры ждущего мультивибратора, справедливы и в данном случае. tu1 = 0,7* R1* C1 , tu2 = 0,7* R2* C2.
Период следования импульсов, как это видно из временных диаграмм на рис. 9,б, равен сумме длительности импульсов: Т = tИ1 + tИ2
Частота следования импульсов, генерируемых мультивибратором, F = 1 / T = 1 / (tu1 + tu2).
Длительность фронта. Фронт выходного импульса имеет экспоненциальную форму в связи с тем, что зарядный ток времязадающего конденсатора протекает через резистор Rк закрытого транзистора и создает падение напряжения на RК, направленное встречно Ек. Поэтому напряжение на коллекторе не может сразу после запирания транзистора установиться на уровне Ек. По мере заряда конденсатора ток заряда и создаваемое им напряжение на Rк уменьшаются, а напряжение на коллекторе закрытого транзистора стремится к установившемуся значению Ек с постоянной времени RК * С, где С=С1 или С2, а RК = RК1 или RК2. Для инженерных расчетов считают, что длительность фронтов равна: tФ1 = 2,3 * RК1 * С2 , tФ2 = 2,3 * RК1 * С2 .
Амплитуда импульсов в отсутствие нагрузки определяется разностью уровней напряжения на коллекторах открытого и закрытого транзистора. Можно считать, что напряжение на коллекторе закрытого транзистора близко к Ек, а на коллекторе открытого примерно равно нулю, т. е. UМ = Ек .
2.5. Регулирование частоты автоколебательного мультивибратора
Поскольку частота колебаний автоколебательного мультивибратора выражается через длительность выходных импульсов, то для ее регулирования применимы те же методы, что и в ждущем мультивибраторе. При этом следует иметь в виду, что для сохранения неизменной скважности регулировку частоты необходимо осуществлять одновременным изменением tu1 и tu2 на одинаковое значение.
Способ регулировки частоты изменением постоянной времени времязадающих цепей имеет те же недостатки, которые отмечались при изучении ждущего мультивибратора. Только увеличение емкости времязадающей цепи в данном случае ведет не к увеличению времени восстановления, а к удлинению фронта выходного импульса. Плавное регулирование частоты мультивибратора может осуществляться по схеме, приведенной на рис. 10. В этом случае для создания смещения на базах транзисторов используется отдельный источник, напряжение которого можно регулировать.
В процессе формирования выходного импульса напряжение на конденсаторе времязадающей цепи меняется по экспоненциальному закону от Ек, стремясь к значению Un. С уменьшением Ecм должна уменьшаться скорость изменения напряжения на конденсаторе (рис. 10,б), это напряжение позже достигает нулевого значения.
2.6. Методы улучшения параметров мультивибратора
Рассмотрим схемы мультивибраторов, позволяющие улучшить параметры импульсов, формируемых ими.
Мультивибратор с отключающими диодами. Недостатком рассмотренных схем является большая длительность фронтов выходных импульсов. Это объясняется тем, что после перехода мультивибратора в следующее квазиустойчивое состояние емкость времязадающей цепи заряжается током, замыкающимся через сравнительно большое коллекторное сопротивление. От этого недостатка свободен мультивибратор с отключающими диодами (рис. 11).
В этом мультивибраторе зарядный ток конденсатора времязадающих цепей замыкается через резисторы \R3 и R4. При этом на указанных резисторах возникают напряжения, которые закрывают соответствующий диод VD1, VD2. Закрытый диод отключает зарядную цепь конденсатора от коллектора транзистора, напряжение на коллекторе достаточно быстро устанавливается на уровне Ек. Конденсаторы заряжаются по той же цепи, что и мультивибратор на рис. 10, так как в это время соответствующий диод открыт, его сопротивление мало и практически не влияет на длительность выходных импульсов. На рис. 11 показано состояние мультивибратора, в котором транзистор VT1 открыт, а VD2 закрыт. В этом состоянии диод VD2 закрыт напряжением с резистора R4, а диод VD1 открыт. Конденсатор C1 заряжается током, протекающим через резистор R4, а конденсатор С2 разряжается через открытый диод VD1.
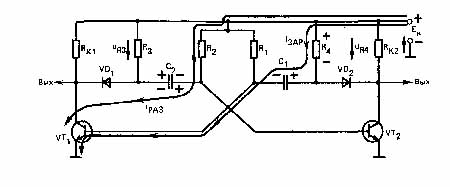
Наиболее существенный недостаток данного мультивибратора состоит в том, что он не может обеспечить высокую скважность импульсной последовательности. Ограниченное значение скважности (Q = 5...6) объясняется следующими причинами. Увеличение скважности требует увеличения отношения tu1 / tu2 . Это приводит к тому, что конденсаторы C1 и C2 должны иметь разную емкость, причем разность емкостей должна быть существенной. В этом случае может оказаться, что конденсатор большей емкости не будет успевать заряжаться через сравнительно большое сопротивление R3, R4 за то время, в течение которого конденсатор меньшей емкости разряжается через R1, R2.
3. Генераторы линейно изменяющегося напряжения
3.1. Общие сведения
Генераторы линейно изменяющегося напряжения (ГЛИН) представляют собой электронные устройства, напряжение на выходе которых в течение некоторого времени изменяется по линейному закону. Часто такое напряжение меняется периодически.
Если напряжение изменяется от меньшего значения к большему (по абсолютному значению), то его называют линейно нарастающим, если от большего значения к меньшему, то - линейно падающим. Периодически изменяющееся напряжение называют пилообразным. Подобные генераторы широко применяются в аппаратуре связи, телевидении, радиолокации. Наиболее часто их используют для создания временной развертки луча в электронно-лучевых трубках осциллографов, телевизоров и т. п.
Другой важной областью применения пилообразного напряжения является преобразование напряжения во временной интервал в устройствах фазоимпульсной модуляции сигналов, при сравнении токов и напряжений и при замене напряжения цифровым кодом и т. п.
В практически используемых схемах генераторов линейно изменяющегося напряжения заложен принцип заряда и разряда конденсатора через резистор при подаче на вход перепада напряжения. Схемные варианты, реализующие этот принцип, различаются лишь методами улучшения параметров формируемого напряжения.
3.2. Простейший генератор линейно изменяющегося напряжения
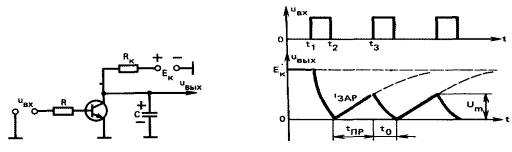
Простейшая схема ГЛИН приведена на рис. 12. Линейно изменяющееся напряжение образуется при заряде конденсатора С через резистор Rк от источника Ек. Транзистор VT, работающий в ключевом режиме, переключает конденсатор с заряда на разряд. Временные диаграммы, поясняющие работу простого ГЛИН, приведены на рис. 13
 |
|
| Рис. 12 | Рис. 13 |
В исходном состоянии до момента t1 транзистор закрыт пороговым напряжением Un, конденсатор С заряжен до напряжения Ек. В момент t1 на его вход поступают импульсы положительной полярности. При поступлении первого импульса транзистор открывается и конденсатор разряжается через открытый транзистор. Длительность импульсов, отпирающих транзистор, устанавливается такой, чтобы конденсатор мог разрядиться практически полностью. В момент t2 действие импульса заканчивается, транзистор запирается и начинается заряд конденсатора в цепи +Ек, RК, C, Ек с постоянной времени RК * С. В этом случае выходная цепь генератора представляет собой удлиняющую RС-цепь, в которой напряжение источника является входным. Напряжение на выходе такой цепи меняется по экспоненциальному закону, стремясь к Ек.
Подаваемый в момент времени t3 второй отпирающий импульс открывает транзистор и прерывает процесс нарастания напряжения на конденсаторе. Если интервал времени между отпирающими импульсами значительно меньше постоянной времени заряда, то в промежутках между входными импульсами на выходе генератора формируется линейно нарастающее напряжение. Выходное напряжение ГЛИН описывается выражением: UВЫХ = UC = Ек ( 1 - exp ( - t/Rк*С)).
Линейно-нарастающее напряжение характеризуется рядом основных параметров. Рассмотрим их на примере напряжения, формируемого простейшим ГЛИН. На рис. 13 поясняются некоторые из параметров: tпр-длительность прямого хода (время, в течение которого происходит заряд конденсатора С через резистор RК, to-длительность обратного хода (время восстановления) - время, в течение которого происходит разряд конденсатора С; T = tnp + to-период повторения пилообразных импульсов; Um- амплитуда пилообразных импульсов; ?-коэффициент нелинейности.
Известно, что линейная функция характеризуется постоянством производной во всех ее точках. Поэтому отклонение от линейного закона можно оценивать коэффициентом нелинейности, определяемым как относительное изменение производной функции, т. е.
α = [ (duВЫХ./dt)НАЧ - (duВЫХ./dt)КОН] / (duВЫХ./dt)НАЧ .
В простейшем ГЛИН Uвых = Uс и это соотношение принимает вид:
α = [ (duС./dt)НАЧ - (duС./dt)КОН] / (duС./dt)НАЧ
где (duС./dt)НАЧ и (duС./dt)КОН - скорость изменения напряжения на конденсаторе в начале и конце прямого хода.
Параметр α характеризует степень отклонения кривой напряжения на конденсаторе от линейно-изменяющегося закона. Этот параметр может быть определен также через ток, протекающий через конденсатор в процессе заряда. Известно, что duС /dt = Ic / C, подставляя это соотношение в предыдущее выражение получаем:
α = [ IC НАЧ - IC КОН] / IC НАЧ
где IC НАЧ и IC КОН - токи, заряжающие конденсатор в начале и конце прямого хода.
Из полученного соотношения видно, что напряжение на конденсаторе будет изменяться по линейному закону в том случае, если ток, протекающий через конденсатор, в процессе его заряда не меняется, т. е. IC НАЧ = IC КОН. Таким образом, степень нелинейности определяется относительным изменением тока, протекающего через конденсатор, в процессе формирования линейного напряжения. Изменение же тока связано с тем, что по мере заряда конденсатора напряжение на нем меняется, вызывая изменение напряжения на Rк, а следовательно, и тока в цепи.
Пользуясь последней формулой, определим коэффициент α для простейшего ГЛИН. Пренебрегаем по сравнению с Ек падением напряжения на RК от тока /кво. Тогда:
α ≈ Uм / Ек
где Uм - напряжение на зарядившемся конденсаторе к концу прямого хода. После несложных преобразование можно получить:
α ≈ tnp / r .
Отсюда видно, что коэффициент нелинейности в простейшем ГЛИН можно уменьшить, увеличив αзар = Rк * С или уменьшив tпр. Объясняется это тем, что в обоих случаях уменьшается длительность используемого участка экспоненты, а чем меньше используемый участок, тем он ближе к линейному.
Последней характеристикой линейно-изменяющегося напряжения является коэффициент использования напряжения источника питания ?, который показывает, насколько амплитуда пилообразного напряжения меньше амплитуды, до которой мог бы зарядиться конденсатор:
ß = Uм / Ек .
Сравнивая последние формулы для схемы простого генератора, можно сделать вывод о том, что для нее ß = α , т. е. коэффициент нелинейности равен коэффициенту использования. Это существенный недостаток простой схемы ГЛИН, поскольку уменьшение α приводит и к уменьшению ß. Если, например, требуется обеспечить коэффициент нелинейности α = 1%, то амплитуда выходного напряжения будет составлять только 0,01Ек.
Значительно улучшить параметры ГЛИН можно используя операционные усилители с обратными связями, которые обладают очень большим коэффициентом усиления. Рассмотрим некоторые из них.
3.3. ГЛИН с отрицательной обратной связью
Принципиальная схема ГЛИН с отрицательной обратной связью через емкость С формирующей цепи показана на рис. 14, а. Здесь и далее приводится условное изображение разрядного ключа SW.
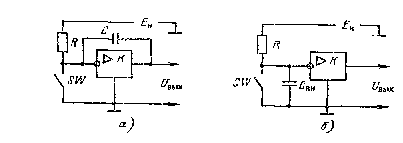
Заменив емкость С на Свн (14,б), получим схему простого ГЛИН, к выходу которого подключен инвертирующий усилитель с коэффициентом усиления К. На выходе усилителя параметры ГЛИН оказываются лучше в (1 + К) раз:
α = tnp / r * (1 + К) .
Таким образом, введение глубокой обратной связи (К >>1) позволяет уменьшить коэффициент нелинейности в (1+ К) раз при неизменном коэффициенте использования α.
В схемах ГЛИН удобно применять современные операционные усилители (К = 104...106) с высоким входным сопротивлением и большой скоростью нарастания выходного напряжения (до 80 В/мкс). Последний параметр ограничивает время восстановления и период повторения ГЛИН.
Некоторым недостатком рассмотренной схемы ГЛИН с ООС может оказаться дрейф постоянной составляющей выходного напряжения операционного усилителя, поскольку он охвачен отрицательной обратной связью только по переменному току.
От этого недостатка свободна схема ГЛИН (рис. 15), в которой ключ SW включен параллельно С, т. е. периодически замыкает выход усилителя на его инвертирующий вход. При этом в конце интервала выходное напряжение практически совпадает с напряжением на прямом входе усилителя.
3.4. ГЛИН с положительной связью
При введении положительной обратной связи (рис. 16, а) через резистор на его верхнем выводе должна действовать сумма напряжений источника питания Ек и Uвых. Заменив R на Rвн (рис. 16, б), получим схему простого ГЛИН, к выходу которого подключен неинвертирующий усилитель с Кп < 1. Для такой схемы коэффициент нелинейности получается минимальным при Кп > 1
α = tnp ( 1 - Кп ) / R * C ,
а коэффициент использования остается неизменным
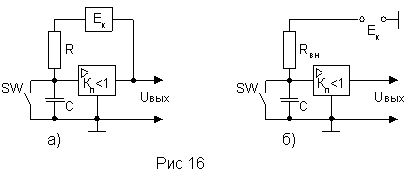
Практические схемы ГЛИН с положительной обратной связью показаны на рис. 17. В первой из них (рис. 17, а) в качестве усилителя с К < 1 используется эмиттерный повторитель на транзисторе VT.
В схеме с операционным усилителем (рис. 17,б) ток фиксации Iф будет втекать в его выходную цепь. Поэтому в схеме необходимо использовать современные операционные усилители с комплементарной парой выходных эмиттерных повторителей. Для получения К< 1 и устранения дрейфа выходного напряжения операционный усилитель на рис. 17, б охвачен отрицательной обратной связью по постоянному току (с выхода на инвертирующий вход), при которой его коэффициент передачи становится равным:
Kп = K / (1+K),
где К - коэффициент усиления без обратной связи
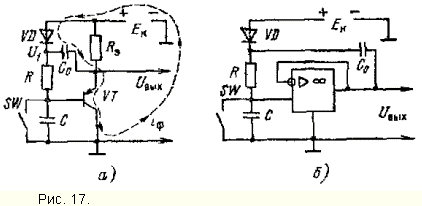
Благодаря большим значениям К операционных усилителей Kп в этом случае ближе к 1, чем в схеме с эмиттерным повторителем, и коэффициент нелинейности значительно меньше.
Сравнивая качества ГЛИН с положительной и отрицательной обратной связью можно сказать, что сравниваемые схемы ГЛИН обеспечивают при равных условиях одинаково хорошие результаты.
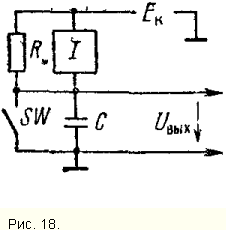
3.5. ГЛИН со стабилизатором тока
В отличие от рассмотренных выше схем в стабилизатор тока вводится обратная связь не по напряжению, а по току, что позволяет повысить внутреннее сопротивление стабилизатора. Эквивалентная схема ГЛИН (рис. 18) содержит идеальный источник тока /, параллельно которому включено внутреннее сопротивление переменному току R.
В ГЛИН со стабилизатором тока можно получить малые коэффициенты нелинейности.
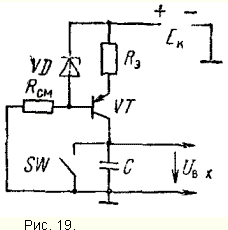
Практическая схема ГЛИН со стабилизатором тока на транзисторе VT показана на рис. 19. Конденсатор С заряжается коллекторным током транзистора.
Отрицательная обратная связь по току создается за счет сопротивления Rэ. При большой глубине обратной связи, внутреннее сопротивление стабилизатора Ri будет определяться выходной проводимостью транзистора в схеме "общая база" и может достигать значений 106 - 108.
Общий недостаток схем ГЛИН со стабилизатором тока - плохая нагрузочная способность, поскольку сопротивление нагрузки оказывается включенным параллельно Ri и увеличивает коэффициент нелинейности
4. Системы счисления
4.1. Общие сведения
По способу представления информации системы связи делятся на аналоговые и цифровые. Общие принципы построения таких систем и их особенности изучаются в соответствующих курсах. Цифровые системы в недалеком будущем займут главенствующее положение. Они состоят из импульсных и вычислительных устройств, осуществляющих усиление, генерирование, формирование, преобразование импульсных сигналов, используемых в системе. Вычислительные устройства выполняют функции хранения и обработки цифровой информации, преобразования информации из аналоговой формы представления в цифровую, и наоборот.
Система изображения любых чисел с помощью ограниченного числа символов называется системой счисления. Используемые в системе счисления символы называются цифрами.
Существуют различные системы счисления, и от их особенностей зависит наглядность представления числа при помощи цифр и сложность выполнения арифметических операций. Если в системе счисления каждой цифре в любом месте числа соответствует одно и то же значение - количественный эквивалент, то такая система счисления называется непозиционной. Таким образом, для непозиционных систем счисления местоположение цифры в записи числа не играет никакой роли.
Примером непозиционной системы счисления является римская система, в которой используются римские цифры I, V, X, L, С, М. Соответственно значение числа, например, CCXXIV вычисляется следующим образом: С=100, Х=10, V=5, I=1. При этом вес цифры не зависит от ее местоположения в записи числа, а знак зависит. Если цифра с меньшим весом стоит слева от цифры с большим весом, то ее знак -, а если цифра с меньшим весом стоит справа от цифры с большим весом то ее знак +. Общим недостатком непозиционных систем счисления являются трудности записи в таких системах больших чисел и трудности выполнения арифметических операций, поскольку для этого используются громоздкие правила. Поэтому в цифровой технике непозиционные системы практически не нашли применения.
В цифровой технике используются позиционные системы счисления. Система счисления называется позиционной, если одна и та же цифра имеет различное значение, которое определяется ее позицией в последовательности цифр, изображающей число. Это значение меняется в однозначной зависимости от позиции цифры по некоторому закону.
В десятичной системе основание р=10 и для записи чисел используется десять цифр: 0, 1, 2, ..., 9. Каждая цифра числа занимает в нем определенный разряд, который имеет весовые коэффициенты для разрядов влево от запятой 100, 101, 102... и вправо от запятой 10-1, 10-2, 10-3, ...
Позиционные системы счисления имеют ряд преимуществ перед непозиционными. Основным преимуществом следует считать удобство выполнения таких арифметических операций, как сложение, вычитание, умножение, деление, извлечение корня и др. Поэтому в цифровой технике, как правило, применяются позиционные системы счисления. Выбор основания системы счисления зависит от физических элементов, на основе которых строится то или иное устройство. В цифровой технике широко используются элементы с двумя устойчивыми состояниями. В этих элементах различие между отдельными фиксированными состояниями носит качественный, а не количественный характер, благодаря чему представление чисел с их помощью может быть реализовано значительно надежнее, чем с помощью элементов, в которых число четко различимых состояний превышает два. В частности, выполнение элемента с десятью четко различимыми состояниями представляет собой сложную техническую задачу. Указанное обстоятельство явилось одной из главных причин распространения в цифровой технике позиционных систем с недесятичным основанием, в первую очередь двоичной, а также восьмеричной и шестнадцатеричной систем счисления.
Наибольшее распространение в цифровой технике имеет двоичная система счисления. В этой системе используются только две цифры: 0 и 1. В двоичной системе любое число может быть представлено последовательностью двоичных цифр:
N2=am am-1 am-2……a0 a-1 a-2 ,
где аi , принимает значение либо 0, либо 1. Эта запись соответствует сумме степеней числа два, взятых с указанными в ней коэффициентами:
N2= am 2m+am-1 2m-1+am-22m-2+….+a0 20+a-1 2-1+a-12-2…
Вес разрядов, отсчитываемых влево от запятой, в целой части числа равен соответственно 1, 2, 4, 8, 16, .... вес же разрядов правее запятой в дробной части будет ?, ?, и т.д. Например, число 11010,112 соответствует следующему количеству:
11010,112= 1*24+1*23+0*22+1*21+0*20+1*1/2+1*1/4
которое, как следует из приведенного разложения его по степеням числа 2, равно десятичному числу 26,7510. В восьмеричной системе счисления употребляется восемь цифр: 0, 1, 2, ..., 7. Любое число в восьмеричной системе представляется последовательностью"
N8=bm bm-1 bm-2……b0 b-1 b-2 ,
в которой цифры bi могут принимать значения от 0 до 7. Вес разрядов целой части 1, 8, 64, 256, ..., в дробной части 1/8, 1/64, 1/256. Например, восьмеричное число 756,2:
756,258 = 7* 82 + 5*81 + 6* 80 + 2.8-1
равно десятичному числу 494, 32812510.
В шестнадцатеричной системе счисления для изображения чисел употребляется 16 цифр: 0... 15. При этом, чтобы одну цифру не изображать двумя символами, приходится вводить специальные обозначения для цифр больше девяти. В качестве шести символов обычно используются буквы латинского алфавита А, В, С, D, Е, F, которым в десятичной системе соответствуют числа 10, 11, 12, 13, 14, 15. Таким образом, шестнадцатеричное число А7В,C8 соответствует следующему количеству:
A7B,C816= 10*162+7*161+11*160+12*16-1+8*16-2, равному десятичному числу 2683,7812510.
4.2. Перевод чисел из одной системы счисления в другую
Основания восьмеричной и шестнадцатеричной систем счисления выражаются целой степенью двух (8=23, 16=24). Этим объясняется простота преобразования чисел, представленных в этих системах, в двоичную систему счисления и обратно.
Для перевода чисел из восьмеричной системы счисления в двоичную достаточно каждую цифру восьмеричного числа представить трехразрядным двоичным числом. Например,
762,358=111 110 010, 011 1012.
Перевод шестнадцатеричных чисел в двоичную систему счисления достигается представлением цифр шестнадцатеричного числа четырехразрядными двоичными числами. Например,
А7В, С716=1010 0111 1011, 1100 01112 .
При обратном переводе чисел из двоичной системы в восьмеричную или шестнадцатеричную системы счисления необходимо разряды двоичного числа, отсчитывая их от запятой влево и вправо, разбить на группы по три разряда в случае перевода в восьмеричную систему или на группы по четыре разряда в случае перевода в шестнадцатеричную систему счисления. Неполные крайние группы дополняются нулями. Затем каждая двоичная группа представляется цифрой той системы счисления, в которую переводится число.
Большую сложность представляет перевод чисел из десятичной в двоичную и обратно. Метод, используемый для такого перевода, зависит от системы счисления, в которой проводятся арифметические операции, необходимые для перевода числа из одной системы счисления в другую. Если перевод осуществляется вручную, то очевидно, операции будут выполняться в десятичной системе счисления, если цифровым устройством, то арифметические операции будут выполняться над числами, представленными в двоичной системе счисления. Целая часть числа преобразуется точно, дробная часть - приближенно.
4.3. Арифметические операции в двоичной системе счисления
Основной операцией, которая используется в цифровых устройствах при выполнении различных арифметических действий, является алгебраическое сложение (сложение, в котором могут участвовать как положительные, так и отрицательные числа). Вычитание легко сводится к сложению путем изменения знака вычитаемого на обратный. Операции умножения и деления также сводятся к сложению и некоторым логическим действиям. Поэтому именно с операции сложения начнем рассмотрение способов выполнения арифметических операций.
При записи кода числа будем знак числа представлять 0 (для положительных чисел) и 1 (для отрицательных чисел). Именно такими цифрами в устройствах, предназначенных для хранения чисел, принято фиксировать знак числа в специально выделяемых так называемых знаковых разрядах. Положение запятой в числе показывать не будем.
Сложение положительных чисел.
Сложение чисел в двоичной системе счисления выполняется на основе таблицы двоичного сложения:
0+0=0
0+1=1
1+0=1
1+1=10
Двузначная сумма в последнем случае означаете что при сложении двух двоичных цифр, равных 1, в каком-либо разряде двоичного числа возникает перенос в соседний старший разряд. Этот перенос должен быть прибавлен к сумме цифр, образовавшейся в соседнем разряде.
При сложении двух многоразрядных двоичных чисел цифры разрядов суммы формируются последовательно, начиная с младшего разряда. Цифра младшего разряда суммы образуется суммированием цифр младших разрядов слагаемых. При этом кроме цифры разряда суммы формируется цифра переноса в следующий, более старший разряд, если оба младших разряда единицы. Таким образом, в разрядах, начиная со второго, могут суммироваться три цифры: цифры соответствующего разряда слагаемых и перенос, поступающий в данный разряд из предыдущего. Этот перенос равен 1 во всех случаях, когда результат суммирования цифр в разряде равен или больше 2, поскольку 2 является основанием системы счисления. При этом в разряд суммы записывается цифра, на две единицы меньшая результата суммирования.
Пример сложения двух многоразрядных двоичных чисел:
1101101 - первое слагаемое
+
1001111 - второе слагаемое
0100010 - поразрядная сумма без учета переносов
+
1 11 1 - переносы
10111100- окончательная сумма.
Непосредственно под двумя слагаемыми записан результат поразрядного сложения без учета переноса. В тех разрядах, в которых оба слагаемых равны единице, поразрядная сумма равна 0. В этих разрядах образовался перенос в соседний старший разряд, который отмечен в следующей строке. В результате сложения строки поразрядных сумм со строкою переносов получается окончательная сумма. При сложении подразрядной суммы с переносами удобно пользоваться следующим правилом: если в результате поразрядного суммирования образовалась группа единиц, расположенных рядом, и в младший разряд этой группы поступает перенос 1, то он переводит все единицы этой группы в нули, а ближайший за рядом единиц 0 - в 1.
Вычитание двух чисел в двоичной системе выполняется на основе таблицы двоичного вычитания
0-0=0,
1-0= 1,
1-1=0,
10-1 = 1.
Если при поразрядном вычитании приходится вычитать из нуля в уменьшаемом единицу в вычитаемом, то делается заем в соседнем старшем разряде, т.е. единица старшего разряда представляется как две единицы данного разряда. Вычитание в этом случае выполняется в соответствии с таблицей. Если в соседнем разряде или в нескольких старших разрядах стоят нули, то заем делается в ближайшем старшем разряде, в котором стоит единица. Эта единица представляется в виде суммы числа, состоящего из единицы во всех промежуточных разрядах, в которых находились нули, и двух единиц в данном разряде. Далее производится подразрядное вычитание в соответствии с таблицей. Естественно, что необходимости в дополнительном заеме во всех промежуточных разрядах появиться не может.
В цифровой технике операция вычитания с использованием заема практически не применяется (за исключением отдельных устройств) и реализуется как алгебраическое сложение с применением специальных кодов для представления отрицательных чисел. При этом операция вычитания сводится к операции простого арифметического сложения при помощи обратного и дополнительного кодов, используемых для представления отрицательных чисел.
Обратный код отрицательных двоичных чисел может быть сформирован по следующему правилу: цифры всех разрядов, кроме знакового, заменяются на обратные (инвертируются)-единицы заменяются нулями, а нули единицами. В знаковый разряд ставится единица. Обратное преобразование из обратного кода в прямой производится по тому же правилу. При использовании обратного кода операция вычитания реализуется как арифметическое сложение положительного числа, представленного в прямом коде, с отрицательным числом, представленным в обратном коде. Например, при вычитании из числа 0 10110 числа 1 01101 уменьшаемое представляется как положительное число в прямом коде 0 10110, а вычитаемое - как отрицательное число в обратном коде 1 10010. В представлении чисел знаковые разряды выделены подчеркиванием. При выполнении операции арифметического сложения над этими числами получаем алгебраическую сумму:
0 10110 - первое слагаемое в прямом коде,
+
1 10010 - второе слагаемое в обратном коде,
+
10 01000
1
0 01001 - сумма в прямом коде.
Перенос, возникающий из знакового разряда, при использовании обратного кода должен прибавляться в младший разряд суммы. В данном примере уменьшаемое по модулю больше вычитаемого, поэтому алгебраическая сумма положительная и представлена в прямом коде. Если уменьшаемое по модулю меньше вычитаемого результатом сложения будет отрицательное число и оно будет представлено в обратном коде.
Дополнительный код отрицательных двоичных чисел может быть сформирован по следующему правилу: цифры всех разрядов, кроме знакового, инвертируются, и в младший разряд прибавляется единица. Дополнительный код может быть получен и из обратного путем прибавления единицы к младшему разряду обратного кода. При этом в знаковый разряд отрицательного числа в дополнительном коде ставится единица. Обратное преобразование из дополнительного кода в прямой производится по тому же правилу.
При использовании дополнительного кода для вычитания двоичных чисел из предыдущего примера получим:
0 10110 - первое слагаемое в прямом коде,
+
1 10011 - второе слагаемое в дополнительном коде,
0 01001 - сумма в прямом коде.
При сложении складываются цифры знаковых разрядов с отбрасыванием возникающего из этого разряда переноса. Алгебраическая сумма, полученная в результате сложения, является положительным числом и поэтому представлена в прямом коде. Если уменьшаемое по модулю меньше вычитаемого результатом сложения будет отрицательное число и оно будет представлено в дополнительном коде.
Умножение двоичных многоразрядных чисел включает в себя две операции - определение знака произведения и определение его абсолютной величины. Знаковый разряд может быть получен суммированием цифр знаковых разрядов сомножителей без формирования переноса:
0+0=0,
0+1=1,
1+0=1,
1+1= 0 - без формирования переноса.
При несовпадении цифр получается 1, что соответствует знаку произведения двух сомножителей с разными знаками.
Абсолютная величина значения произведения определяется путем перемножения чисел без учета их знаков. Перемножение многоразрядных двоичных чисел производится на основе таблицы двоичного умножения
0х0=0,
0х1=0,
1х0=0,
1х1=1.
При умножении двух двоичных чисел множимое последовательно умножается на каждую цифру множителя, начиная либо с младшей, либо со старшей, и для учета веса соответствующей цифры множителя сдвигается либо влево, если умножение производится, начиная с младшего разряда множителя, либо вправо, если умножение производится, начиная со старшего разряда множителя, на такое число разрядов, на которое соответствующий разряд множителя сдвинут относительно младшего или старшего разряда.
Получающиеся в результате умножения и сдвига частичные произведения после суммирования дают полное произведение. Особенность умножения двоичных чисел состоит в том, что частичное произведение может быть либо сдвинутым на соответствующее число разрядов множимым, если соответствующая цифра множителя равна 1, либо нулем, если соответствующая цифра множителя равна 0:
10111 - множимое,
*
1101 - множитель
10111 - первое частичное произведение
00000 - второе частичное произведение
10111 - третье частичное произведение
10111 - четвертое частичное произведение
100101011 - произведение
Тот же результат можно получить при умножении, начиная со старших разрядов множителя и сдвигая частичные произведения вправо.
В цифровых устройствах процессу суммирования частичных произведений придают последовательный характер: формируется одно из частичных произведений, к нему с соответствующим сдвигом прибавляется следующее частичное произведение, к полученной сумме прибавляется с соответствующим сдвигом очередное частичное произведение, и т. д., пока не окажутся просуммированными все частичные произведения и не будет получено полное произведение.
При таком методе все частичные произведения суммируются с требуемыми сдвигами друг относительно друга, благодаря чему образуется ранее приведенный результат умножения этих чисел.
Если требуется сохранить все разряды в произведении, то в разрядной сетке устройства должно быть предусмотрено число разрядов, равное сумме числа разрядов множимого и множителя. Однако при умножении дробных чисел часто в произведении требуется иметь то же число разрядов, что и в множимом. В таком приближенном представлении результата не фиксируются цифры разрядов при сдвигах. Таким образом, цифры младших разрядов окажутся потерянными и будет получен приближенный результат. Далее отбрасывается последний из разрядов, и если этот разряд содержит 1, то 1 прибавляется к следующему разряду для округления результата.
Если множимое, или множитель, или оба вместе содержат и целую и дробную части, то запятые в множимом и множителе не учитываются, они умножаются как два целых числа и от полученного произведения справа отделяются запятой m+n разрядов, где n - число дробных разрядов множимого, a m - число дробных разрядов множителя.
Деление двоичных многоразрядных чисел включает в себя две операции-определение знака частного и определение его абсолютной величины.
Знаковый разряд частного может быть получен, как и знаковый разряд произведения, суммированием цифр знаковых разрядов делимого и делителя без формирования переноса. Абсолютная величина частного определяется делением чисел без учета их знаков.
Деление начинается с того, что от делимого слева отделяется группа разрядов, причем количество разрядов в этой группе должно либо равняться количеству разрядов в делителе, либо быть на один разряд больше. Если отделение такой группы возможно, в старший разряд частного записывается 1, в противном случае в разряд единиц частного записывается нуль. Если выявилось, что частное содержит целую часть, то образуется новая группа разрядов путем вычитания из выделенной группы делителя и приписывания к разности очередной цифры делимого. Если в результате получилось число, превышающее делитель, то в частное записывается 1, в противном случае следующая цифра будет равна 0.
В дальнейшем выполняется ряд одинаковых циклов. Если последняя цифра частного была равна 1, то новая группа образуется вычитанием делителя из предыдущей группы и приписыванием очередной цифры делимого. Если последняя цифра частного 0, то для образования новой группы достаточно приписать к предыдущей группе очередную цифру делимого. Последняя цифра целой части частного получается тогда, когда после определения очередной цифры частного 1 или 0 в делимом не останется больше цифр для того, чтобы приписывать их к разности между предыдущей группой и делителем или ь самой предыдущей группе. После этого начинается выделение дробных членов частного. Оно отличается от вычисления целых членов только тем, что вместо очередных цифр делимого к предыдущим группам приписываются нули.
В цифровых устройствах при выполнении операции деления так же, как и при выполнении операции алгебраического сложения, используется дополнительный и модифицированный коды.
4.4. Формы представления чисел с фиксированной и плавающей точками
В вычислительной технике применяют две формы представления чисел: с фиксированной точкой (запятой) и с плавающей точкой (запятой). Эти формы называют также соответственно естественной и полулогарифмической. Множество чисел, которые могут быть изображены с помощью n двоичных разрядов, представляет собой на числовой оси ряд из 2n равностоящих точек с дискретностью, т. е. расстоянием между точками, равной весу младшего разряда, который заполняет некоторую область между Nmin и Nmax. Любое число между Nmin и Nmax может быть изображено с абсолютной погрешностью, не превышающей половины младшего разряда. Относительная погрешность зависит от абсолютной величины числа и может меняться в широких пределах.
Представление числа таким способом называется представлением с фиксированной точкой. Такое название связано с тем, что точка, отделяющая дробную часть от целой, фиксируется в определенном месте относительно разрядов числа. Обычно точка находится или перед старшим разрядом, или после младшего. В первом случае могут быть представлены только числа по модулю меньшие единицы, а во втором случае-только целые числа. На рис. 20,а показаны примеры форматов для представления двоичных чисел с фиксированной точкой. Для кода знака выделяется знаковый разряд - обычно крайний слева. В знаковом разряде 1 соответствует минусу, а 0 - плюсу. На рис. 20,а показан формат для числа с точкой, фиксированной перед старшим разрядом. В этом формате могут быть представлены числа - правильной дроби с точностью до 2-(n-1). При этом диапазон представления чисел будет
2-(n-1) > | N | > 1 - 2-(n-1).
Если точка фиксирована справа от младшего разряда, то при п разрядах можно представить целые числа в диапазоне
1 >| N | > 2-(n-1) - 1.
По сравнению с выполнением действий над дробными числами использование целочисленной арифметики позволяет более экономно расходовать оборудование, так как для достижения требуемой точности нет необходимости учитывать большое количество младших разрядов, как это имеет место при оперировании правильными дробями. Кроме того, выравнивание по младшим разрядам уменьшает вероятность возникновения переполнения разрядной сетки, т.е. появления результата, превышающего максимально допустимый при данном числе разрядов.
Кроме способа представления чисел с фиксированной точкой широкое распространение получил другой способ - представление чисел с плавающей точкой. При этом число представляется в виде:
N = ±q, ±m,
что соответствует следующей записи:
N = р±q (± m),
где р - основание системы счисления; q - целое число, выражающее порядок числа N; m - мантисса числа, причем всегда выполняется неравенство |m| > 1 (рис. 20, б). Запись числа в таком виде называется полулогарифмической потому, что в логарифмической форме представляется не все число, а только его часть р±q. При полулогарифмической записи положение точки в мантиссе m определяется величиной порядка q. С изменением порядка в большую или меньшую сторону точка перемещается влево или вправо, т. е. "плавает" в изображении числа.
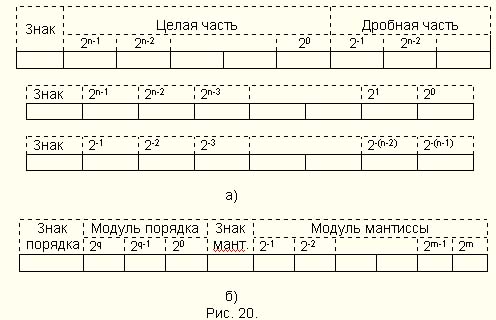
Представление числа в форме р±q (± m) не является однозначным, так как его значение не изменится при записи в разрядах мантиссы числа m*qk вместо m и числа (q-k) в разрядах порядка вместо q. Поэтому на изображение числа в форме с плавающей точкой накладывается еще одно дополнительное условие, чтобы независимо от значения числа абсолютная величина мантиссы изменялась в узких пределах. Число, представленное в записи р±q (± m), называется нормализованным, если мантисса удовлетворяет условию
1 > | т | > 1/р,
т. е. если старший разряд мантиссы в системе счисления с основанием р отличен от нуля.
Операция преобразования ненормализованного числа в нормализованное называется нормализацией. Для выполнения операции нормализации под знак числа отводится два разряда. Если нормализованное двоичное число положительно, то в старшем цифровом разряде должна стоять 1, а если оно отрицательное -то 0. Сочетание 01 и 10 в знаковом и старшем цифровых разрядах означает выполнение одного из условий нормализации
1/2 > | m | ,
а сочетание 00 и 11 в этих же разрядах - нарушение этого условия. Для нормализации числа в данном случае следует повторять цикл сдвига цифровой части влево на один разряд (умножение на 2) с одновременным вычитанием единицы из порядка (деление на 2) до тех пор, пока не начнет выполняться условие нормализации.
Нормализацию можно осуществить сдвигом мантиссы вместе со знаком на один разряд вправо с одновременным добавлением единицы к порядку.
При выполнении действий над числами с плавающей точкой определенные операции выполняются как над мантиссами, так и над порядками. Для упрощения операций над порядками их сводят к действиям над целыми положительными числами - без знака, применяя представление чисел с плавающей точкой со смещенным порядком. В случае представления числа с плавающей точкой со смещенным порядком к его порядку q прибавляется целое число - смещение
М = 2k, где k - число двоичных разрядов, используемых для модуля порядка. Смещенный порядок
qсм = q + М
будет всегда положительным. Для его представления необходимо такое же число разрядов, как и для модуля и знака порядка q. Важная особенность смещенных порядков состоит в том, что если для порядков p1 и p2, представляющих собой целые числа со знаками, выполняется соотношение p1 > p2, то и для положительных целых чисел соответствующих смещенных порядков p1 см и р2 см также будет выполняться соотношение р1 см > р2 см.
Точность вычислений при представлении чисел с плавающей точкой определяется числом разрядов мантиссы. При фиксированном числе разрядов мантиссы любая величина мантиссы представляется с наиболее возможной точностью нормализованным числом.
Диапазон представимых чисел при использовании форм записи с фиксированной и плавающей точками в случае одной и той же системы счисления и при равном количестве разрядов, используемых для записи чисел, будет различным. Диапазон чисел, представимых в n разрядах в представлении с фиксированной точкой,
Pm > | N |> рl - рm при l + m = n,
где l - число разрядов, отведенных для представления целой части числа; m - число разрядов, используемых для записи дробной части.
При использовании формы записи числа с плавающей точкой диапазон представимых чисел будет
P - pn > N > ( 1 - p-m) ppn
где q - количество разрядов, отводимых для записи порядка, а m - для записи мантиссы.
Из сравнения этих двух соотношений вытекает, что при одинаковом числе разрядов форма представления числа с плавающей точкой обеспечивает более широкий диапазон чисел.
5. Логические основы вычислительной техники
5.1. Понятие о логической функции и логическом устройстве
Для обозначения различных предметов, понятий, действий пользуются словами. Слова строятся из букв, которые берутся из некоторого их набора, называемого алфавитом.
В цифровой технике для тех же целей пользуются кодовыми словами. Особенность этих слов состоит в том, что все они имеют одинаковую длину (т. е. представляют собой последовательность букв одинаковой длины) и для их построения используется простейший алфавит, состоящий лишь из двух букв. Эти буквы принято обозначать символами 0 и 1. Таким образом, кодовое слово в цифровой технике есть последовательность символов 0 и 1 определенной длины, например 10111011. Такими словами могут представляться и числа, в этом случае 0 и 1 совпадают по смыслу с обычными арабскими цифрами. При представлении кодовым словом некоторой нечисловой информации, чтобы отличать буквы 0 и 1 от цифр, будем эти буквы называть соответственно логическим нулем и логической единицей.
Если длина кодовых слов составляет n разрядов, то можно построить 2n различных комбинаций - кодовых слов. Например, при n=3 можно построить 23 = 8 слов: 000, 001, 010, O11, 100, 101, 110, 111.
Информация, которая передается между отдельными узлами (блоками) сложного цифрового устройства, представляется в виде кодовых слов. Таким образом, на входы каждого узла поступают кодовые слова, на выходе узла образуется новое кодовое слово, представляющее собой результат обработки входных слов. Выходное слово зависит от того, какие слова поступают на входы узла. Поэтому можно говорить, что выходное слово есть функция, для которой аргументами являются входные слова. Для того чтобы подчеркнуть особенность таких функций, состоящую в том, что сама функция и ее аргументы могут принимать значения лог. 0 и лог. 1, будем эти функции называть функциями алгебры логики (ФАЛ).
Устройства, предназначенные для формирования функций алгебры логики, в дальнейшем будем называть логическими устройствами или цифровыми устройствами.
Цифровые устройства (либо их узлы) можно делить на типы по различным признакам.
По способу ввода и вывода кодовых слов различают логические устройства последовательного, параллельного и смешанного действия.
На входы устройства последовательного действия символы кодовых слов поступают не одновременно, а последовательно, символ за символом (в так называемой последовательной форме). В такой же последовательной форме выдается выходное слово.
На входы устройства параллельного действия все n символов каждого входного кодового слова подаются одновременно (в так называемой параллельной форме). В такой же форме образуется на выходе выходное слово. Очевидно, при параллельной форме приема и выдачи кодовых слов в устройстве необходимо иметь для каждого разряда входного (выходного) слова отдельный вход (выход).
В устройствах смешанного действия входные и выходные кодовые слова представляются в разных формах. Например, входные слова - в последовательной форме, выходные - в параллельной. Устройства смешанного действия могут использоваться для преобразования кодовых слов из одной формы представления в другую (из последовательной формы в параллельную или наоборот).
По способу функционирования логические устройства (и их схемы) делят на два класса: комбинационные устройства (и соответственно комбинационные схемы) и последовательностные устройства (последовательностные схемы).
В комбинационном устройстве (называемом также автоматом без памяти) каждый символ на выходе (лог. 0 или лог. 1) определяется лишь символами (лог. 0 или лог. 1.), действующими в данный момент времени на входах устройства, и не зависит от того, какие символы ранее действовали на этих входах, В этом смысле комбинационные устройства лишены памяти (они не хранят сведений о прошлом работы устройства).
В последовательностных устройствах (или автоматах с памятью) выходной сигнал определяется не только набором символов, действующих на входах в данный момент времени, но и внутренним состоянием устройства, а последнее зависит от того, какие наборы символов действовали во все предшествующие моменты времени. Поэтому можно говорить, что последовательностные устройства обладают памятью (они хранят сведения о прошлом работы устройства).
Рассмотрим примеры комбинационного и последовательностного устройств.
Пусть устройство предназначено для формирования на выходе сигнала, определяющего совпадение сигналов на входах: на выходе формируется лог. 1 в случаях, когда на обоих входах действует лог. 1 либо на обоих входах действует лог. 0; если на одном из входов действует лог. 1, а на другом-лог. 0, то на выходе устройства образуется лог. 0. Такое устройство является комбинационным, в котором значение формируемой на выходе логической функции определяется лишь значениями ее аргументов в данный момент времени.
Рассмотрим другой пример. Счетчик подсчитывает импульсы. В каждый момент времени его состояние соответствует числу поступивших на вход импульсов. Выходная информация определяется тем, каково было состояние счетчика до данного интервала времени и поступает или нет на вход импульс в этом интервале времени. Таким образом, данное устройство является последовательностным устройством.
5.2. Элементарные логические функции
В классической математике для задания функции обычно используются два способа: аналитический (запись формулой) и табличный (таблицами значений функции, какие приводятся, например, в справочниках). Подобными же способами могут задаваться логические функции.
При использовании табличного способа задания логических функций строится так называемая таблица истинности, в которой приводятся все возможные сочетания значений аргументов и соответствующие им значения логической функции. Так как число таких сочетаний конечно, таблица истинности позволяет определять значение функции для любых значений аргументов (в отличие от таблиц математических функций, которые позволяют задавать значения функции не для всех, а лишь для некоторых значений аргументов).
Таблица истинности функций двух аргументов представлена в табл. 1. Существует всего четыре функции одного аргумента.
Таблица 1
Если число аргументов функции равно n, то число различных сочетаний (наборов) значений аргументов составляет 2n, а число различных функций п аргументов-22n. Так, при n=2 число наборов значений аргументов равно 22=4, число функций 24=16. Таблица истинности логических функций двух аргументов представлена в табл. 2.
Возможен и аналитический способ записи логической функции. В обычной математике аналитический способ представления функции предполагает запись функции в виде математического выражения, в котором аргументы функции связываются определенными математическими операциями. Подобно этому аналитический способ задания логической функции предусматривает запись функции в форме логического выражения, показывающего, какие и в какой последовательности должны выполняться логические операции над аргументами функции.
Функции одного агрумента (табл. 1) представляются следующими выражениями:
f1(x) = 0 (константа 0); f2(x)=x;
f3(х) = х; f4(х) = 1 (константа 1).
Устройства, реализующие функции f1(x), f2(x) и f4(x), оказываются тривиальными. Таким образом, из всех функций одного аргумента практический интерес может представлять лишь функция f3(х), которую называют инверсией или логическое НЕ.
Из таблиц истинности функций f0 - f15 (табл. 2) наиболее широко используемыми являются:
f1(x1,x2) = x1*x1 - конъюнкции, логическое произведение, И;
f7(x1,x2) = x1 + x2 - дизъюнкции, логическое сложение, ИЛИ;
f14(x1,x2) = x1 + x2 - логическое И-НЕ;
f14(x1,x2) = x1 * x2 - логическое ИЛИ-НЕ.
Остальные из приведенных в табл. 2 функций либо, либо используются редко.
В дальнейшем функции одного и двух аргументов будем называть элементарными логическими функциями, имея в виду, что логические выражения этих функций, содержащие не более одной логической операции, элементарны.
Свойства конъюнкции, дизъюнкции и инверсии.
Конъюнкция переменных х1 и х2 равна лог. 1 в том случае, когда и x1 и x2 равны лог. 1 (отсюда возникло название операции логическое И).
Дизъюнкция переменных х1 и x2 равна лог. 1, если или х1 или x2 равны лог. 1 (отсюда понятно возникновение названия операции логическое ИЛИ).
В тех случаях, когда число переменных больше двух, конъюнкция их равна лог. 1 при равенстве лог. 1 всех переменных; дизъюнкция равняется лог. 1, если хотя бы одна из них равна лог. 1.
В математике установлен определенный порядок выполнения операций в сложном выражении. Например, вначале выполняется операция умножения и затем операция сложения. Если требуется изменить этот порядок, используются скобки.
Подобно этому и для сложного логического выражения установлен определенный порядок выполнения операций: вначале выполняются операции инверсии, затем операции конъюнкции и в последнюю очередь операции дизъюнкции. Например, запись логического выражения х1+х2*x3+x4*x2 предполагает, что при вычислении выражения вначале выполняются операции инверсии х3 и затем операции конъюнкции х2*x3 и в последнюю очередь - операции дизъюнкции. А если требуется нарушить это правило, используются скобки. В этом случае вначале выполняются операции в скобках (а если одни скобки вложены в другие, то вначале выполняются операции в самых внутренних скобках).
Операции конъюнкции и дизъюнкции обладают рядом свойств:
сочетательный закон : x1*(x2*x3) = (x1*x2)*x3
x1+(x2+x3) = (x1+x2)+x3;
переместительный закон: x1*x2 = x2*x1
x1+x2 = x2+x1;
распределительный закон: x1+(x2*x3) = (x1+x2) * (x1+x3).
Легко убедиться в справедливости следующих выражений:
1*х=х; х*х=х; 1+x=1; х+х=х;
0*х=0; х * х =0; 0+х=х; х + х = 1 .
Кроме того, существуют так называемые формулы де Моргана:
x1+x2 = x1 * x2 и x1*x2 = x1 + x2
Можно сформулировать следующее правило применения формул де Моргана к сложным логическим выражениям. Инверсия любого сложного выражения, в котором аргументы (либо их инверсии) связаны операциями конъюнкции и дизъюнкции, может быть представлена тем же выражением без инверсии с изменением всех знаков конъюнкции на знаки дизъюнкции, знаков дизъюнкции на знаки конъюнкции и инверсией всех аргументов.
5.3. Полные системы функции алгебры логики
Очевидно, могут быть построены простейшие логические элементы, реализующие элементарные логические функции двух переменных f0,..., f15. Сложные логические функции могут быть построены последовательным выполнением функциональных зависимостей, связывающих пары переменных.
Следовательно, имея элементы, осуществляющие элементарные операции f0,..., f15 можно выполнить любую сложную логическую операцию. Такую систему функций можно назвать полной системой, или базисом. Условие наличия 16 различных типов логических элементов, каждый из которых реализует одну из 16 элементарных функций /о,..., /is, является достаточным для синтеза логического устройства любой сложности, но оно не является необходимым, т. е. при синтезе можно ограничиться меньшим набором элементарных функций, взятых f0,..., f15.
Последовательно исключая из базиса функции, можно получить так называемый минимальный базис. Под минимальным базисом понимают такой набор функций, исключение, из которого любой функции превращает полную систему функций в неполную.
Возможны различные базисы и минимальные базисы, отличающиеся друг от друга числом входящих в них функций и видом этих функций. Выбор того или иного базиса для синтеза логических устройств связан с тем, насколько просто, удобно и экономично технически выполнить элементы, реализующие входящие в базис функции, и в целом все логическое устройство.
Как показано выше, с помощью логических операций конъюнкции (И), дизъюнкции (ИЛИ) и инверсии (НЕ) можно выразить любую другую из элементарных функций f0,..., f15. Следовательно, эта совокупность логических функций образует базис. Это означает, что любая логическая функция, как бы сложна она ни была, может быть представлена через логические операции И, ИЛИ, НЕ. Иначе, можно построить любое логическое устройство, имея лишь три типа логических элементов, выполняющих операции И, ИЛИ,НЕ.
Однако, базис И, ИЛИ, НЕ не является минимальным. Из этой совокупности функций можно исключить функцию И либо функцию ИЛИ и оставшийся набор функций будет удовлетворять свойствам базиса. Действительно, если исключить функцию И, то операцию И можно выразить через оставшиеся операции ИЛИ и НЕ. Чтобы показать это, нужно дважды проинвертировать конъюнкцию и применить затем правило де Моргана.
Хотя операцию И и можно выразить через операции ИЛИ и НЕ, но это сложно (требуется выполнение трех операций инверсии и одной операции ИЛИ), поэтому на практике используется неминимальный базис, включающий в себя все три функции И, ИЛИ, НЕ.
В настоящее время базис И, ИЛИ, НЕ обычно используется при начальной стадии проектирования устройств для построения функциональной схемы. Для реализации устройств обычно используются базисы И-НЕ либо ИЛИ-НЕ. Элементы этого базиса широко выпускаются промышленностью в интегральном исполнении.
5.4. Логические элементы, общие сведения
Выше отмечалось, что логические функции и их аргументы принимают значение лог. 0 и лог. 1. При этом следует иметь в виду, что в устройствах лог. 0 и лог. 1 соответствует напряжение определенного уровня (либо формы). Наиболее часто используется два способа физического представления лог. 0 и лог. 1: потенциальный и импульсный.
При потенциальной форме для представления лог. 0 и лог. 1 используется напряжение двух уровней: высокий уровень соответствует лог. 1 (уровень лог. 1) и низкий уровень соответствует лог. 0 (уровень лог. 0). Такой способ представления значений логических величин называется положительной логикой. Относительно редко используют так называемую отрицательную логику, при которой лог. 1 ставят в соответствии низкий уровень напряжения, а лог. 0 - высокий уровень. В дальнейшем, если это не оговаривается особо, будем пользоваться только положительной логикой.
При импульсной форме лог. 1 соответствует наличие импульса, логическому 0 - отсутствие импульса.
Заметим, что, если при потенциальной форме соответствующая сигналу информация (лог. 1 либо лог. 0) может быть определена практически в любой момент времени, то при импульсной форме соответствие между уровнем напряжения и значением логической величины устанавливается в определенные дискретные моменты времени (так называемые тактовые моменты времени).
5.5. Основные параметры интегральных логических элементов
Рассмотрим основные параметры логических элементов и методы их улучшения.
Коэффициент объединения по входу определяет число входов элемента, предназначенных для подачи логических переменных. Элемент с большим коэффициентом объединения по входу имеет более широкие логические возможности.
Нагрузочная способность (или коэффициент разветвления по выходу) определяет число входов аналогичных элементов, которое может быть подключено к выходу данного элемента. Чем выше нагрузочная способность элементов, тем меньшее число элементов может потребоваться при построении цифрового устройства.
Для повышения нагрузочной способности в элементах применяют усложненную схему инвертирующей части. Повышение нагрузочной способности элемента связано с тем, что выходной транзистор, через который замыкается ток нагрузки, удерживается в открытом состоянии большим базовым током, который обеспечивается эмиттерной цепью транзистора.
В выключенном состоянии элемента с простым инвертором ток в нагрузку, подается от источника питания через коллекторный резистор с большим сопротивлением. Этот резистор ограничивает максимальное значение тока в нагрузке (с ростом тока нагрузки увеличивается падение напряжения на Rк, уменьшается напряжение на выходе). В элементе со сложным инвертором в нагрузку подается эмиттерный ток транзистора, работающего в схеме эмиттерного повторителя. Так как выходное сопротивление эмиттерного повторителя мало, то выходное напряжение слабее зависит от тока нагрузки и допустимы большие значения нагрузочного тока.
Быстродействие логических элементов является одним из важнейших параметров логических элементов, оно оценивается задержкой распространения сигнала от входа к выходу элемента.
Рассмотрим факторы, влияющие на быстродействие логического элемента, и методы повышения быстродействия.
Для повышения скорости переключения транзисторов в элементе необходимо использовать более высокочастотные транзисторы и переключение транзисторов производить большими управляющими токами в цепи базы; существенное уменьшение времени задержки достигается благодаря использованию ненасыщенного режима работы транзисторов (в этом случае исключается время, необходимое на рассасывание неосновных носителей в базе при выключении транзисторов).
Задержка распространения сигнала связана также с необходимостью перезарядки емкости нагрузки и паразитных монтажных емкостей. Этот процесс можно ускорить следующими приемами:
уменьшением Rк (и, следовательно, уменьшением постоянной времени Rк*С); однако при этом растут потребляемые от источника питания ток и мощность;
использованием в элементе малых перепадов напряжения;
применением на выходе элемента эмиттерного повторителя, уменьшающего влияние подключенной к выходу емкости нагрузки.
Помехоустойчивость определяется максимальным значением помехи, не вызывающей нарушения работы элемента.
Для количественной оценки помехоустойчивости воспользуемся так называемой передаточной характеристикой логического элемента (инвертора). На рис. 21 приведена типичная форма этой характеристики. Передаточная характеристика представляет собой зависимость выходного напряжения от входного. Для ее получения необходимо соединить все входы логического элемента и, изменяя напряжение на входе, отмечать соответствующие значения напряжения на выходе. При увеличении входного напряжения от нуля до порогового уровня лог. 0 -Un, напряжение на выходе уменьшается от уровня лог. 1 до некоторого минимально допустимого уровня лог. 1 - U1min. Дальнейшее увеличение входного напряжения приводит к резкому снижению выходного. При больших значениях входного напряжения, превышающих пороговый уровень лог. 1 U1min, на выходе устанавливается напряжение, не превышающее максимально допустимого уровня лог. 0 - U0max. Таким образом, при нормальной работе элемента в статическом (установившемся) режиме недопустимы входные напряжения U0п < Uвx < U1п.
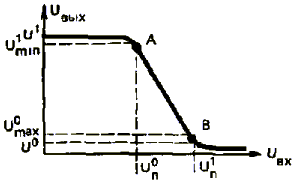
Допустимыми считаются такие помехи, которые, наложившись на входное напряжение, не выведут его в область недопустимых значений U0п < Uвx <;U1п.
6. Комбинационные цифровые устройства
6.1. Типовые КЦУ
В цифровой технике при построении сложных устройств широко применяются не только отдельные логические элементы, реализующие элементарные булевы функции, но и их комбинации в виде типовых структур, выполняемых как единое целое в виде интегральных микросхем. На входы таких структур могут подаваться информационные логические сигналы и сигналы управления. Последние могут определять, например, порядок передачи информационных входных сигналов на выход или играть роль сигналов синхронизации. Во многих случаях, особенно при использовании в устройствах выходных цепей с тремя состояниями, в качестве сигналов синхронизации выступают сигналы "Выбор микросхемы" (CS). Наличие активного значения такого сигнала управления (в одних схемах это логический нуль, в других - логическая единица) разрешает устройству выполнение заданных функций, отсутствие его переводит схему в "невыбранное" состояние, при котором она не выполняет обработку информации, а ее выходы отключены от нагрузки. Рассмотрим типовые КЦУ.
6.2. Шифраторы
Шифратор (называемый также кодером) - устройство, осуществляющее преобразование десятичных чисел в двоичную систему счисления. Пусть в шифраторе имеется m входов, последовательно пронумерованных десятичными числами (0, 1, 2, 3, ... ..., m - 1), и n выходов. Подача сигнала на один из входов приводит к появлению на выходах n-разрядного двоичного числа, соответствующего номеру возбужденного входа.
Очевидно, трудно строить шифраторы с очень большим числом входов m, поэтому они используются для преобразования в двоичную систему счисления относительно небольших десятичных чисел.
Шифраторы широко используются в разнообразных устройствах ввода информации в цифровые системы. Такие устройства могут снабжаться клавиатурой, каждая клавиша которой связана с определенным входом шифратора. При нажатии выбранной клавиши подается сигнал на определенный вход шифратора, и на его выходе возникав двоичное число, соответствующее выгравированному на клавише символу.
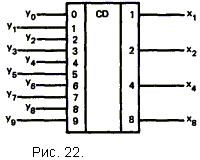
На рис. 22 приведено символическое изображение шифратора, преобразующего десятичные числа 0, 1, 2, ..., 9 в двоичную. Символ CD образован из букв, входящих в английское слово CODER. Слева показано 10 входов, обозначенных десятичными цифрами 0, 1, ..., 9. Справа показаны выходы шифратора: цифрами 1, 2, 4, 8 обозначены весовые коэффициенты двоичных разрядов, соответствующих отдельным выходам.
Из приведенной таблицы истинности (табл. 3) следует, что переменная х1 на выходной шине 1 имеет уровень лог. 1, если возбуждается один из нечетных входов. Следовательно:
X1 = y1 + y3 + y5 + y7 + y9.
Аналогично для остальных выходов:
x2 = y2 + y3 + y6 +y7 ,
x4 = y4 + y5 + y6 + y7 ,
x8 = y8 + y9 .
Этой системе логических выражений соответствует схема на рис. 23, а. На рис. 23, б изображена схема шифратора на элементах ИЛИ-НЕ.
При выполнении шифратора на элементах И-НЕ предусмотрена подача на входы инверсных значений, т. е. для получения на выходе двоичного представления некоторой десятичной цифры необходимо на соответствующий вход подать лог. 0, а на остальные входы-лог.1. Схема шифратора, выполненная на элементах И-НЕ, приведена на рис. 23,в.
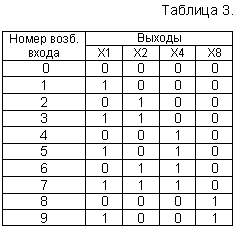
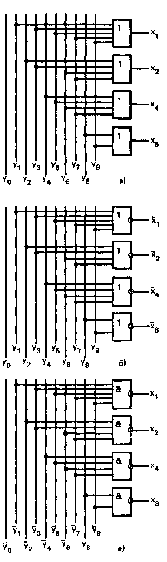
Изложенным способом могут быть построены шифраторы, выполняющие преобразование десятичных чисел в двоичное представление с использованием любого двоичного кода.
6.3. Дешифраторы
Для обратного преобразования двоичных чисел в небольшие по значению десятичные числа используются дешифраторы (называемые также декодерами). Входы дешифратора предназначаются для подачи двоичных чисел, выходы последовательно нумеруются десятичными числами. При подаче на входы двоичного числа появляется сигнал на определенном выходе, номер которого соответствует входному числу.
Дешифраторы имеют широкое применение. В частности, они используются в устройствах, печатающих на бумаге выводимые из цифрового устройства числа или текст. В таких устройствах двоичное число, поступая на вход дешифратора, вызывает появление сигнала на определенном его выходе. С помощью этого сигнала производится печать символа, соответствующего входному двоичному числу.
На рис. 24, а приведено символическое изображение дешифратора. Символ DC образован из букв английского слова DECODER. Слева показаны входы, на которых отмечены весовые коэффициенты двоичного кода. Справа - выходы, пронумерованные десятичными числами, соответствующими отдельным комбинациям входного двоичного кода. На каждом выходе образуется уровень лог. 1 при строго определенной комбинации входного кода.
Дешифратор может иметь парафазные входы для подачи наряду с входными переменными их инверсий, как показано на рис. 24,б.
По способу построения различают линейны ей прямоугольные дешифраторы.
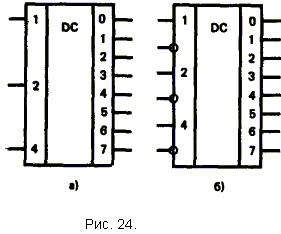
6.4. Мультиплексоры
Мультиплексор является устройством, которое осуществляет коммутацию одного из нескольких информационных входных сигналов на выход в соответствии с заданным кодом на входах управления. Мультиплексор имеет несколько информационных входов (D0, D1,...),, входы управления(A0, A1, ...) и один выход Q. На рис. 25, а показано символическое изображение типичного мультиплексора с четырьмя информационными входами и входом синхронизации С.
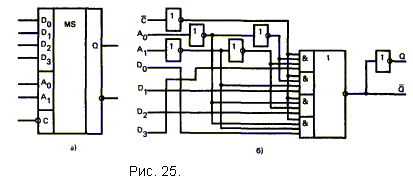
Каждому информационному входу мультиплексора присваивается номер, называемый адресом. При подаче сигнала на вход С мультиплексор выбирает один из входов, адрес которого задается двоичным кодом на входах управления, и подключает его к выходу.
Таким образом, подавая на адресные входы адреса различных информационных входов, можно передавать цифровые сигналы с этих входов на выход Q.
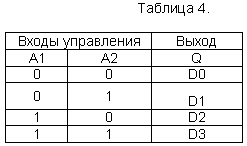
Функционирование мультиплексора определяется табл. 4 (при С=1).. При отсутствии стробирующего сигнала (С=0) связь между информационными входами и выходом отсутствует (Q=0). При подаче стробирующего сигнала (С=1) на выход передается логический уровень того из информационных входов Di, номер которого i в двоичной форме задан на адресных входах.
Принципиальная схема мультиплексора показана на рис. 25, б.
В тех случаях, когда требуется передавать на выходы многоразрядные входные данные в параллельной форме, используется параллельное включение мультиплексоров по числу разрядов передаваемых данных.
6.5. Демультиплексоры
Демультиплексор имеет один информационный вход и несколько выходов. Он представляет собой устройство, которое осуществляет коммутацию информационного входного сигнала на один из выходов, имеющему адрес (номер), задаваемый на входах управления. На рис. 26 показано символическое изображение демультиплексора с четырьмя выходами. Функционирование этого демультиплексора определяется табл. 5.

Структурные формулы, определяющие формирование выходных сигналов такого демультиплексора, имеют вид:
y0 = x1 * x2 * D, y2 = x1 * x2 * D ,
y0 = x1 * x2 * D, y0 = x1 * x2 * D .
Использование демультиплексора может существенно упростить построение логического устройства, имеющего несколько выходов, на которых формируются различные логические функции одних и тех же переменных.
6.6. Одноразрядный двоичный сумматор
Из рассмотренного ранее принципа сложения многоразрядных двоичных чисел следует, что в каждом из разрядов производятся однотипные действия: определяется цифра суммы путем сложения по модулю 2 цифр слагаемых и поступающего в данный разряд переноса и формируется перенос, передаваемый в следующий разряд. Эти действия реализуются одноразрядным двоичным сумматором. Символическое изображение такого сумматора показано на рис. 27, а. Он имеет три входа для подачи цифр разрядов слагаемых ai, bi и переноса рi ; на выходах формируются сумма si, и перенос pi + 1, i предназначенный для передачи в следующий разряд.
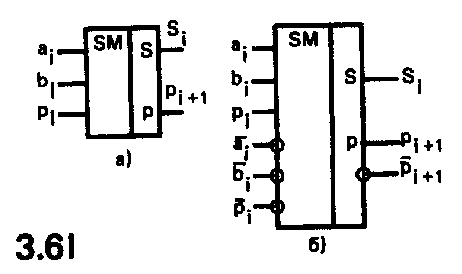
В одноразрядном сумматоре могут предусматриваться входы для подачи как прямых значений разрядов слагаемых ai, bi и переноса рi, так и инверсных значений, а также выходы, на которых формируются инверсные значения выходных переменных. Пример такого одноразрядного сумматора приведен на рис. 27, б.
В таблице 6 показан закон функционирования одноразрядного сумматора.
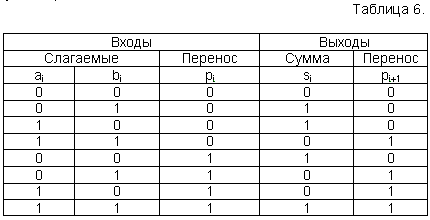
6.7. Многоразрядные двоичные сумматоры
В зависимости от способа ввода разрядов слагаемых сумматоры делятся на два типа: последовательного и параллельного действия. В сумматоры первого типа разряды чисел вводятся в последовательной форме, т. е. разряд за разрядом (младшим разрядом вперед), в сумматоры второго типа каждое из слагаемых подается в параллельной форме, т. е. одновременно всеми разрядами.
Сумматор последовательного действия. Состоит из одноразрядного
сумматора, выход pi+1 которого соединен с входом pi через элемент задержки, параметры которого согласованы со скоростью поступления разрядов слагаемых на входы сумматора. Операция суммирования во всех разрядах слагаемых осуществляется с помощью одного и того же одноразрядного сумматора, но последовательно во времени, начиная с младших разрядов. Такое построение сумматора возможно за счет того, что слагаемые поступают в последовательной форме.
Очевидное достоинство сумматора последовательного действия заключается в малом объеме оборудования, требуемого для его построения. Однако связанная с этим необходимость в последовательной обработке разрядов приводит к крайне низкому быстродействию. Поэтому, сумматоры такого типа в настоящее время используются очень редко.
Сумматор параллельного действия. Состоит из отдельных разрядов, каждый из которых содержит одноразрядный сумматор (рис. 28).
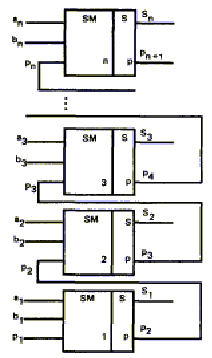
При подаче слагаемых цифры их разрядов поступают на соответствующие одноразрядные сумматоры. Каждый из одноразрядных сумматоров формирует на своих выходах цифру соответствующего разряда суммы и перенос, передаваемый на вход одноразрядного сумматора следующего (более старшего) разряда. Такая организация процесса организации переноса, называемая последовательным переносом, снижает быстродействие многоразрядных сумматоров, т.к. получение результата в старшем разряде сумматора обеспечивается только после завершения распространения переноса по всем разрядам.
Повышение быстродействия параллельных сумматоров. Для обеспечения высокого быстродействия параллельные сумматоры должны строиться на элементах, обладающих высоким быстродействием.
В наиболее неблагоприятном случае возникший в младшем разряде перенос может последовательно вызывать переносы во всех остальных разрядах. При этом время передачи переносов t = t1 * n, где t1 -задержка распространения переноса в одном разряде.
Уменьшение t достигается следующими приемами.
1. При построении схем одноразрядных сумматоров стремятся к уменьшению числа элементов в цепи между входом, на который поступает импульс переноса рi и .выходом, на котором формируется передаваемый в следующий разряд импульс переноса pi+i.
2. В цепях от pi к pi+1 применяют элементы с повышенным быстродействием.
3. Схемы сумматоров следует строить таким образом, чтобы сигналы с выхода каждого логического элемента в цепи от рi, к pi+i поступали на возможно меньшее число других логических элементов, так как присоединение каждого дополнительного элемента к той или иной точке цепи переносов, как правило, приводит к увеличению паразитной емкости, удлинению фронтов сигналов и, следовательно, к увеличению задержки распространения сигнала и снижению быстродействия сумматора.
4. Применяют устройства формирования переносов в параллельной форме. В показанном на рис. 29 сумматоре с помощью устройства, называемого блоком ускоренного переноса, производится формирование переносов в параллельной форме, т. е. одновременно для всех разрядов. Переносы из этого блока поступают во все разрядные сумматоры одновременно. При этом разрядные сумматоры не содержат цепей формирования переносов, они формируют только сумму Si и величины Yi и Xi, для получения которых переносы не требуются. Эти величины YI и Xi необходимы для формирования переносов в блоке ускоренного переноса, они определяют следующие ситуации: Yi=1 означает, что в i-м разряде перенос pi+1 в следующий (p+1)-й разряд необходимо формировать независимо от поступления в данный разряд переноса из предыдущего разряда; Xi=1 означает, что в i-м разряде перенос рi+i должен формироваться только при условии поступления переноса рi, из предыдущего разряда:
Yi = a1 * b1; X1 = (a1 + b1) * p1.
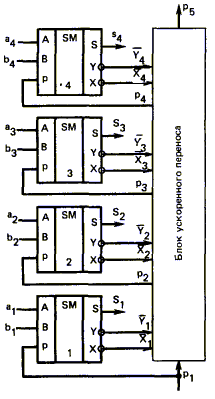
Величины Yi и Xi формируются одновременно во всех разрядных сумматорах, одновременно поступают на входы блока ускоренного переноса и, следовательно, в этом блоке одновременно формируются переносы, подаваемые в разрядные сумматоры. После поступления переносов из блока ускоренного переноса в разрядных сумматорах формируются суммы Si.
6.8. Быстродействие КЦУ
Так как логические элементы, входящие в состав КЦУ, переключаются с задержкой tзад., то при изменении в некоторый момент времени комбинации входных сигналов выходные сигналы устройства (если они изменяются в результате этого) примут установившиеся значения только после того, как закончатся переходные процессы в соответствующих логических элементах. На пути от входов устройства к его выходам отдельные логические элементы включены последовательно. Поэтому длительность переходных процессов будет зависеть от числа логических элементов, которые включены в такой цепочке. Применяемая в настоящее время методика определения tзад в логических элементах, предусматривающая использование при измерении цепочки включенных друг за другом однотипных логических элементов, позволяет при оценке общей задержки в такой цепочке суммировать задержки отдельных логических элементов. При оценке быстродействия КЦУ необходимо выявить ту цепочку логических элементов между входами и выходами устройства, которая будет задавать наибольшую задержку, и сложить между собой задержки логических элементов этой цепочки. Обычно она содержит наибольшее число включенных друг за другом от входов до выходов логических элементов. Но могут быть исключения, связанные, например, с наличием в более короткой цепочке отдельных инерционных логических элементов с большим tзад. Поэтому в общем случае необходимо проанализировать все цепочки логических элементов от входов до выходов и выявить такую, которая дает наибольшую задержку.
6.9. Состязания в КЦУ
Неодинаковую задержку прохождения сигнала в отдельных частях КЦУ иногда ассоциируют с "состязаниями" в скорости переключения логических элементов. В результате этого явления на выходах некоторых элементов могут появляться импульсные помехи. В некоторых случаях неодинаковая задержка прохождения сигнала в отдельных цепочках логических элементов может привести к импульсной помехе и на выходе КЦУ. Покажем это на примере.
Рассмотрим КЦУ представленную на рис. 30, а. Входной сигнал изменяется с кода 1000 на код 1111. Задержка в каждом логическом элементе tзад. Структурная схема КЦУ и временные диаграммы для данного примера приведены на рис. 30, б. В данном случае на выходе КЦУ при изменении кода входного сигнала 1000 на код 1111 кратковременно устанавливается нулевое значение (на время 3 * tзад), хотя по условиям работы выходное значение должно было сохраниться на единичном уровне
Это непосредственно вытекает из временных диаграмм, если пренебречь задержками переключения логических элементов Когда длительность помехи превысит определенную величину, возможно нарушение работоспособности подключенных к выходу КЦУ устройств (триггеров, счетчиков и т. д.). В подобных случаях "состязания" называют "опасными". Для борьбы с "опасными состязаниями" можно принять различные меры. Во-первых, иногда можно предусмотреть такой порядок смены входных кодов, при котором либо импульсные помехи не будут появляться на выходе вообще, либо их длительность уменьшится до безопасной величины. В необходимых случаях такую задержку можно ввести искусственно включением цепочки из четного числа инверторов. Во-вторых, при синтезе соответствующего КЦУ можно иногда найти такой вариант структурной формулы (а следовательно, и структурной схемы), при котором удается уменьшить величину импульсной помехи.
В подобных случаях "состязания" называют "опасными". Для борьбы с "опасными состязаниями" можно принять различные меры. Во-первых, иногда можно предусмотреть такой порядок смены входных кодов, при котором либо импульсные помехи не будут появляться на выходе вообще, либо их длительность уменьшится до безопасной величины. В необходимых случаях такую задержку можно ввести искусственно включением цепочки из четного числа инверторов. Во-вторых, при синтезе соответствующего КЦУ можно иногда найти такой вариант структурной формулы (а следовательно, и структурной схемы), при котором удается уменьшить величину импульсной помехи.
В-третьих, можно организовать синхронную передачу сигналов от одного устройства к другому. Для этого вводятся специальные импульсы синхронизации, которые задают моменты передачи информации между отдельными устройствами. Пауза между импульсами синхронизации может быть выбрана такой, чтобы за ее время закончились переходные процессы и на выходах устройств установились стационарные значения.
Синхронная передача информации в современных цифровых устройствах применяется очень широко. Этот вопрос уже обсуждался ранее, например при рассмотрении типовых КЦУ, в том числе мультиплексоров. Отметим, что наличие "состязаний" и возникающие при этом импульсные помехи влияют на надежность цифровых устройств.

