Разностные уравнения – это алгоритм функционирования дискретной цепи. Разностное уравнение записывается непосредственно по схеме.

Пример: Составить разностное уравнение.

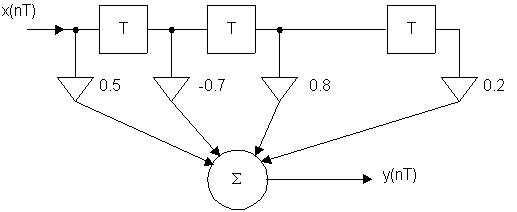
y(nT) = 0.5·x(nT) + (-0.7) ·x(nT-T) + 0.8·x(nT-2T) + 0.2·x(nT-3T)

Пример: Определить y(nT) если x(nT)={1;0.5} для цепи:

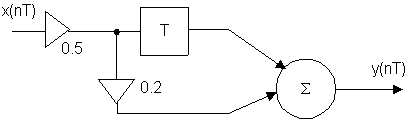
y(nT) = 0.1·x(nT) + 0.5·x(nT-T)

Воспользуемся численным методом.

n=0; y(0T) = 0.1·x(0T) + 0.5·x(-T) = 0.1 + 0.5·0 = 0.1

n=1; y(1T) = 0.1·x(1T) + 0.5·x(0T) = 0.1·0.5 + 0.5·1 = 0.55

n=2; y(2T) = 0.1·x(2T) + 0.5·x(1T) = 0.1·0 + 0.5·0.5 = 0.25

n=3; y(3T) = 0.1·x(3T) + 0.5·x(2T) = 0.1·0 + 0.5·0 = 0

y(nT) = {0.1; 0.55; 0.25}

Пример: Определить сигнал на выходе, если x(nT) = {1; 1}

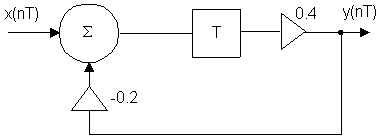
Цепь с обратной связью.

Составим разностное уравнение из двух слагаемых:

y(nT) = 0.4·x(nT-T) – 0.2·0.4·y(nT-T)

вх.сигнал вых.сигнал

n=0; y(0T) = 0.4·x(-T) – 0.08·y(-T) = 0, где: x(-T) = y(-T) = 0

n=1; y(1T) = 0.4·x(0T) – 0.08·y(0T) = 0.4·x(T-T) – 0.08·y(T-T) = 0.4·1-0.08·0 = = 0.4

n=2; y(2T) = 0.4·x(1T) – 0.08·y(1T) = 0.4·1 – 0.08·0.4 = 0.4 – 0.032 = 0.368

n=3; y(3T) = 0.4·x(2T) – 0.08·y(2T) = 0.4·0 – 0.08·0.368 = –0.02944

n=…

y(nT) = {0; 0.4; 0.368; –0.2944; …}

Цепь дискретная, содержащая обратную связь, называется рекурсивной, а цепь, не содержащая обратной связи, называется не рекурсивной.