10.1. Нелинейные элементы. Их характеристики и свойства

10.2. Графические методы расчета цепей с нелинейными резистивными двухполюсниками

10.3. Графические методы расчета цепей с нелинейными резистивными четырехполюсниками

10.4. Эквивалентные преобразования схем с нелинейными элементами

10.5. Аналитическое представление вольт-амперных характеристик

10.6. Аналитические методы расчета нелинейных резистивных цепей

10.7. Стабилизация постоянного напряжения нелинейными резистивными цепями

10.8. Вопросы и задания для самопроверки

10.1. Нелинейные элементы. Их характеристики и свойства

Нелинейные резистивные элементы

Напомним, что нелинейными называются электрические цепи, у которых реакции и воздействие связаны нелинейными зависимостями. Подобные цепи содержат один или несколько приборов, замена которых линейными моделями приводит к недопустимому нарушению количественной и качественной картины колебаний в цепи.

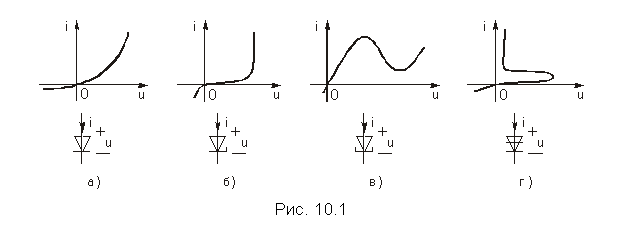
Резистивными нелинейными цепями будем называть цепи, которые допустимо считать нелинейными безынерционными цепями. В соответствии с этим модель нелинейной резистивной цепи не содержит реактивных элементов. В нее входят хотя бы один нелинейный безынерционный резистивный двухполюсник или многополюсник, хотя бы один источник напряжения или тока и то или иное число резистивных сопротивлений.

Для построения многих функциональных узлов аппаратуры связи используется большой класс нелинейных двухполюсных полупроводниковых и электронных приборов, называемых диодами. Единственной электрической характеристикой диода является его вольт-амперная характеристика (ВАХ) - зависимость постоянного тока в диоде от постоянного напряжения на его зажимах i = F(u) при согласном выборе положительных направлений напряжения и тока. Отличительные особенности вольт-амперных характеристик некоторых типов диодов различного назначения и их условные (схемные) обозначения приведены на рис. 10.1. Это характеристики полупроводниковых приборов: выпрямительного диода (рис. 10.1, а), стабилитрона (рис. 10.1, б), туннельного диода (рис. 10.1, в) и динистора (рис. 10.1, г). Характеристики рис. 10.1, а, б получили наименование однозначных, а рис. 10.1, в, г - многозначных, так как у них одному и тому же значению тока (рис. 10.1, в) или напряжения (рис. 10.1, г) соответствуют разные напряжения и токи.

Существуют и электронные приборы с подобными характеристиками.

В последующем, простоты ради, нелинейные резистивные двухполюсники будем называть нелинейными резисторами. Схемное изображение нелинейного резистора приведено на рис. 10.2.

Некоторые из нелинейных резисторов относятся к числу управляемых нелинейных элементов. Управляющей величиной может быть, например, внешняя температура, давление или освещенность. Свойства таких резисторов определяются не одной, а семейством ВАХ, каждая из которых соответствует различным значениям управляющей величины.

Транзисторы, электронные лампы, тиристоры и некоторые другие полупроводниковые и электронные приборы могут рассматриваться как нелинейные резистивные четырехполюсники. Например, при включении транзистора рис. 10.3, а, являющегося трехполюсником, в электрическую цепь один из зажимов оказывается общим для пары входных и пары выходных зажимов транзистора. Поэтому транзистор принято рассматривать как четырехполюсник с двумя парами зажимов. На рис. 10.3, б показано такое включение транзистора по схеме с общим эмиттером.

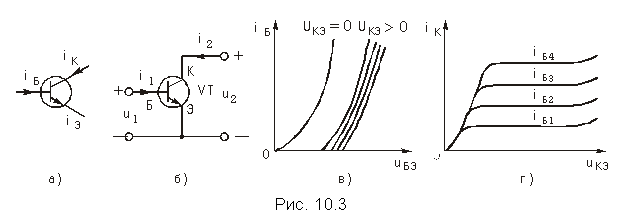
Нелинейный четырехполюсник, как и линейный, описывается двумя уравнениями, которые связывают напряжения и токи на его входе и выходе. При анализе транзисторов часто используется следующая система уравнений:

Для включения транзистора по схеме с общим эмиттером (рис. 10.3, б) u₁ = u_БЭ – напряжение между базой и эмиттером, i₂ = i_К – ток коллектора, i₁ = i_Б – ток базы и u₂ = u_КЭ – напряжение между коллектором и эмиттером.

Уравнения (10.1) и (10.2) изображаются в виде графиков. Так u₁ зависит от двух переменных i₁ и u₂ и, вообще говоря, его графическое изображение представляет собой поверхность в трехмерном пространстве. Так как начертить такую поверхность трудно, то функцию двух переменных изображают на плоскости в виде семейства характеристик: фиксируется одна переменная и непрерывно изменяется другая.

Графическое изображение уравнений (10.1) и (10.2) для транзистора в схеме с общим эмиттером показано на рис. 10.3, в и г. Это так называемые входная и выходная вольт-амперные характеристики. Принято говорить, что ВАХ транзистора управляются током или напряжением. Так, выходная ВАХ транзистора в схеме с общим эмиттером управляется током базы.

ВАХ нелинейных полупроводниковых и электронных приборов находятся, как правило, в результате измерений и приводятся в соответствующих справочниках в виде усредненных графических зависимостей. Необходимость усреднения связана с большим (до 30—50%) технологическим разбросом характеристик различных образцов прибора одного и того же типа. Эти характеристики являются статическими, т. е. характеристиками режима постоянного тока.

Для резистивных нелинейных элементов (НЭ) важным параметром является их сопротивление, которое в отличие от линейных резисторов не является постоянным, а зависит от того, в какой точке ВАХ оно определяется. Различают два вида сопротивлений: статическое и дифференциальное (динамическое). Статическое сопротивление R_ст определяется как (рис. 10.4)

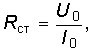
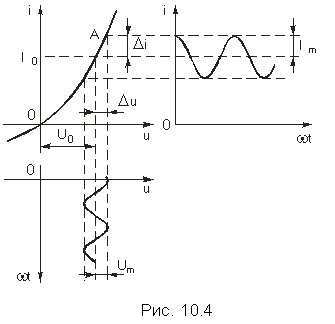
где U₀ – приложенное к НЭ постоянное напряжение; I₀ – протекающий через НЭ постоянный ток. Это сопротивление постоянному току; оно характеризуется тангенсом угла наклона прямой, проходящей через начало координат и рабочую току (U₀, I₀) на ВАХ НЭ.

В силу предположения о резистивном характере цепи статические характеристики определяют одновременно и соотношения между мгновенными значениями напряжений и токов на внешних зажимах соответствующего нелинейного прибора.

Определим дифференциальное сопротивление R_д как отношение приращения напряжения Du к приращению тока Di при небольшом смещении рабочей точки на ВАХ под воздействием переменного напряжения малой амплитуды (рис. 10.4):

Это сопротивление представляет собой сопротивление НЭ переменному току малой амплитуды. Обычно переходят к пределу этих приращений и определяют дифференциальное сопротивление в виде

Оно характеризуется тангенсом угла наклона касательной к ВАХ в рабочей точке.

Иногда удобно пользоваться понятием дифференциальной крутизны (имеющей смысл проводимости)

Нелинейные индуктивные элементы

Типичными динамическими нелинейными элементами электрической цепи являются катушки с сердечниками из ферромагнитных материалов – сплавов на основе металлов группы железа или их оксидов – ферритов. Нелинейность таких элементов обусловлена характеристикой намагничивания материала сердечника B(H). Поскольку в приближении теории магнитных цепей для замкнутого неразветвленного сердечника с постоянным сечением s и длиной l средней магнитной линии магнитный поток Ф пропорционален индукции B: Ф = Bs, а напряженность H связана с током i в обмотке, имеющей w витков, соотношением H = iw/l, то вид зависимости B(H) предопределяет характер вебер-амперной характеристики катушки Y(i) (Y = Фw – потокосцепление обмотки). Типичная вебер-амперная характеристика индуктивного элемента приведена на рис. 10.5, а. В общем случае вид ВАХ индуктивного элемента определяется многими факторами, и она часто является неоднозначной. Например, при циклическом намагничивании сердечника зависимость Y(i) имеет гистерезисный характер (рис. 10.5, б). В этом случае процесс перемагничивания сопровождается необратимыми потерями в сердечнике.

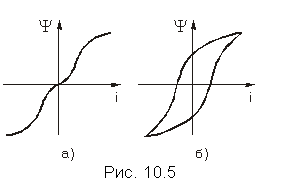
Нелинейный элемент индуктивности характеризуется согласно (1.8) статической индуктивностью L_ст = Y/i и дифференциальной индуктивностью L_д = dY/di, которые зависят от намагничивающего тока i.

Нелинейные емкостные элементы

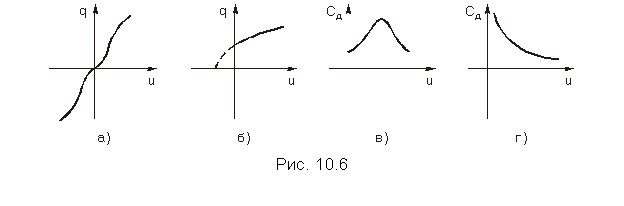
Нелинейные емкостные элементы могут служить моделями конденсаторов, диэлектрическая проницаемость e которых является функцией от напряженности электрического поля E в диэлектрике. Такие емкостные элементы описываются нелинейной вольт-кулоновой характеристикой – зависимостью заряда q от приложенного напряжения u. Подобными свойствами обладают, в частности, сегнетоэлектрики, вольт-амперные характеристики которых, аналогичны характеристикам ферромагнетиков (рис. 10.6, а); обратно смещенные p-n-переходы (рис. 10.6, б) и др.

Нелинейный элемент емкости характеризуется согласно (1.11) статической емкостью С_ст = q/u_с и дифференциальной емкостью С_д = dq/du_с, которые зависят от приложенного напряжения u_с.

На рис. 10.6, в, г, показан характер изменения дифференциальной емкости для вольт-кулонных характеристик, изображенных на рис. 10.6, а и б, соответственно.

10.2. Графические методы расчета цепей с нелинейными резистивными двухполюсниками

Задача нахождения начальных постоянных напряжений и токов на внешних зажимах нелинейных полупроводниковых или электронных приборов, входящих в электрическую цепь, сводится к задаче анализа режима постоянного тока в исследуемой цепи, т. е., к анализу нелинейной резистивной цепи с источниками постоянного напряжения или (и) тока. Решаются подобные задачи обычно с использованием графических построений.

Ниже рассматривается задача анализа режима постоянного тока в электрической цепи с одним нелинейным двухполюсником, – нелинейным резистивным элементом (НЭ). Его ВАХ считается известной и заданной графически.

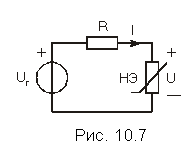
Рассмотрим простейшую электрическую цепь, изображенную на рис. 10.7. В нее входят источник постоянного напряжения с задающим напряжением U_г, линейный резистивный элемент R и нелинейный резистивный элемент, в котором подлежат определению постоянные напряжение U =U₀ и ток I = I₀. Рассмотрим два случая НЭ: с однозначной и многозначной ВАХ.

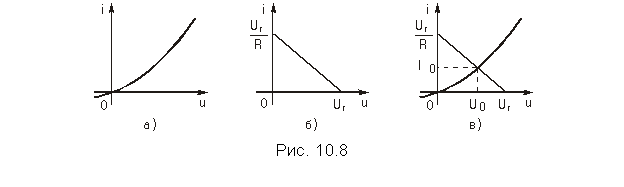
Нелинейный резистивный элемент с однозначной характеристикой

Пусть однозначная ВАХ нелинейного резистивного элемента имеет вид, показанный на рис. 10.8, а.

Согласно ЗНК (рис. 10.7) напряжение U = U_г—RI, и ток в элементе R связан с напряжением U на зажимах НЭ зависимостью I = (U_г—U)/R, представляющей собой прямую, проходящую через точки U_г на оси абсцисс и U_г/R – на оси ординат. Поскольку нелинейный и линейный элементы соединены последовательно, то ВАХ НЭ и прямая I = (U_г—U)/R, определяющие один и тот же ток, удовлетворяются одновременно, чему на графиках рис. 10.8, в соответствует точка их пересечения. Она и определяет искомые значения постоянных напряжения U₀ и тока I₀ в нелинейном резисторе, или, как принято говорить, его рабочую точку.

Графические построения, связанные с решением задачи, всегда выполнимы, а найденное ее решение – единственное.

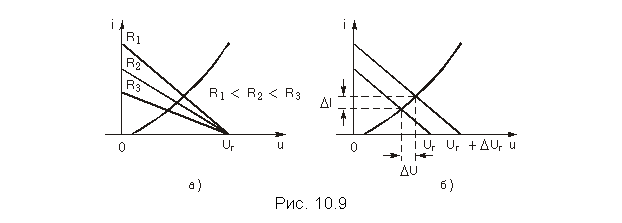
Рабочая точка нелинейного резистора изменяется как с изменением сопротивления R, так и с изменением задающего напряжения источника U_г. Изменение сопротивления R приводит к изменению наклона зависимости I = (U_г—U)/R и смещению рабочей точки на вольт-амперной характеристике нелинейного резистора (см. рис. 10.9, а). Изменение задающего напряжения на величину DU_г вызывает перемещение той же зависимости параллельно самой себе и изменение тока и напряжения в нелинейном резисторе соответственно на величины DI и DU (см. рис. 10.9, б).

Напомним, что отношение бесконечно малого приращения тока к бесконечно малому приращению напряжения на нелинейном элементе, обусловленных смещением рабочей точки, называется дифференциальной проводимостью (крутизной), а обратное отношение – дифференциальным сопротивлением нелинейного резистора в его рабочей точке.

Отношение постоянных тока и напряжения в рабочей точке нелинейного резистора определяет его статистическую проводимость, а обратное отношение – статическое сопротивление резистора в его рабочей точке.

Статическая проводимость пассивного нелинейного резистора всегда положительна. Положительна и дифференциальная проводимость нелинейного резистора с однозначной вольт-амперной характеристикой в силу возрастающего характера последней. Заметим также, что статическая и дифференциальная проводимости линейного резистора не отличаются одна от другой.

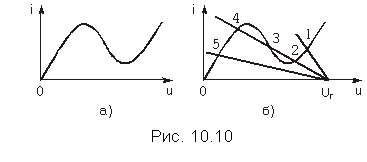
Нелинейный резистивный элемент с многозначной характеристикой

Пусть многозначная ВАХ нелинейного резистивного элемента в схеме рис. 10.7 имеет вид, показанный на рис. 10.10, а. Это характеристика туннельного диода. Для нахождения рабочей точки на ВАХ резистивного НЭ применим те же, что и выше, графические построения.

На рис. 10.10, б совмещены графики вольт-амперной характеристики нелинейного резистора и зависимостей I = (U_г—U)/R для трех различных значений сопротивления линейного резистора R и одного и того же значения напряжения задающего источника U_г.

Анализ рис. 10.10, б показывает, что рабочими точками могут быть точки 1 и 5, соответствующие единственному решению уравнений I = F(U) и I = (U_г—U)/R. Рабочими точками могут быть также точка 2 или точка 4. Точка 3, расположенная па ниспадающем участке ВАХ, является точкой неустойчивого равновесия. Можно показать, что если зафиксировать сопротивление R, при котором могут существовать три точки пересечения указанных зависимостей, и увеличивать задающее напряжение источника от нуля до величины U_г, то рабочей будет точка 4. Если же задающее напряжение источника от очень большого значения уменьшать до значения U_г, то рабочей будет точка 2.

Итак, в цепи с нелинейным двухполюсником, имеющим многозначную ВАХ задачи нахождения рабочей точки не всегда имеет единственное решение.

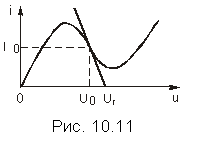
Рабочая точка может быть расположена и на ниспадающем участке вольт-амперной характеристики, если выбрать сопротивление R и задающее напряжение U_г так, как показано на рис. 10.11. Заметим, что в рабочей точке, расположенной на ниспадающем участке вольт-амперной характеристики, дифференциальная проводимость и дифференциальное сопротивление нелинейного резистора отрицательны, поскольку малым положительным значениям приращения напряжения (тока) на зажимах нелинейного резистора соответствуют отрицательные значения приращения тока (напряжения).

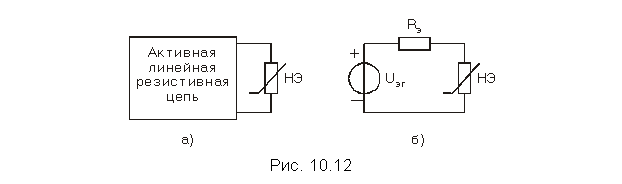
Метод эквивалентного генератора

Изложенная методика определения рабочей точки в цепи с одним линейным и одним нелинейным резистивными элементами распространяется на резистивные цепи с одним резистивным НЭ и произвольным числом линейных резистивных элементов и источников постоянного напряжения или (и) тока, если воспользоваться теоремой об эквивалентном генераторе. Для этого следует внешнюю по отношению к нелинейному двухполюснику линейную активную цепь (см. рис. 10.12, а) заменить эквивалентным генератором с задающим напряжением U_эг и внутренним линейным резистивным эквивалентным сопротивлением R_э (рис. 10.12, б). Тогда схема анализируемой цепи не будет отличаться от схемы рис. 10.7, и задача нахождения рабочей точки сводится к рассмотренной выше.

Напряжения и токи в элементах цепи, внешней по отношению к НЭ, можно найти, воспользовавшись теоремой замещения. Для этого нелинейный резистивный элемент следует заменить источником напряжения (источником тока), напряжение (ток) которого равно (равен) найденному значению напряжения (тока) в рабочей точке. Напряжения и токи в линейной части электрической цепи находят любым методом анализа режима постоянного тока.

Метод, с использованием эквивалентного генератора, является графоаналитическим, поскольку в нем аналитические методы определения параметров эквивалентного генератора и расчета линейной цепи после замены НЭ источником напряжения или тока сочетаются с графическим методом нахождения рабочей точки.

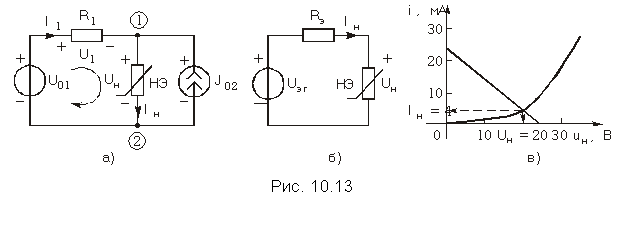
Пример. Применим метод эквивалентного генератора к схеме рис. 10.13, а, где U₀₁ = 14 В, J₀₂ = 10 мА, R₁ = 1 кОм, I_н = 10^–5U_н². Из рисунка следует, что напряжение U_эг при отключении НЭ равно

а эквивалентное сопротивление R_э = R₁ = 1 кОм. В соответствии с ЗНК (рис. 10.13, б) имеем

Построение графиков прямой линии и ВАХ нелинейного элемента показано на рис. 10.13, в. Пересечение этих кривых дает координаты рабочей точки: I_н = 4 мА и U_н = 20 В.

10.3. Графические методы расчета цепей с нелинейными резистивными четырехполюсниками

Рассмотрим задачу анализа режима постоянного тока в резистивной электрической цепи с нелинейным четырехполюсником (рис. 10.14).

Пусть входная ВАХ и семейство выходных ВАХ будут иметь вид показанный на рис. 10.15, а и б; управляющим параметром для семейства выходных характеристик четырехполюсника является его входной ток I₁.

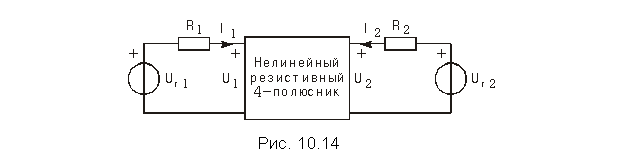
Задача нахождения входных напряжения U₁ = U₁₀ и тока I₁ = = I₁₀ сводится к задаче нахождения рабочей точки на входной вольт-амперной характеристике i₁ = F₁(u₁). Она решается с помощью графических построений, которые полностью аналогичны рассмотренным в 10.2. Графические методы расчета цепей с нелинейными резистивными двухполюсниками (рис. 10.16, а).

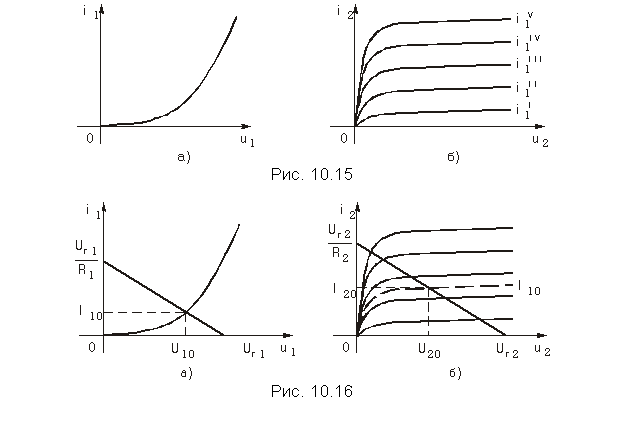
Найденному входному току I₁ = I₁₀ соответствует определенная выходная вольт-амперная характеристика i₂ = F₂(u₂). Она может быть измерена или, как это обычно делается, определена по семейству выходных вольт-амперных характеристик четырехполюсника из справочника. Для этого необходимо провести линейное интерполирование двух характеристик семейства с ближайшими значениями параметров I₁ < I₁₀ и I₁ > I₁₀. На рис. 10.16, б эта характеристика изображена штриховой линией.

Выходной ток I₂ и выходное напряжение U₂ (см. рис. 10.14) связаны между собой линейной зависимостью I₂ = (U_г2—U₂)/R₂, которая на рис. 10.16, б представляет собой прямую, проходящую через точки U₂ =U_г2 на оси абсцисс и I₂ = U_г2/R₂ на оси ординат.

Точка пересечения зависимостей I₂ = (U_г2—U₂)/R₂ и i₂ = F₂(u₂) при I₁ = I₁₀ и определяет рабочую точку (U₂₀, I₂₀) на выходных характеристиках четырехполюсника.

Дальнейший анализ рассматриваемой цепи может быть связан с нахождением напряжений и токов в ветвях входной и выходной цепей, если до анализа эти цепи были заменены эквивалентными генераторами.

10.4. Эквивалентные преобразования схем с нелинейными элементами

Суть эквивалентных преобразований состоит в замене участков цепи с параллельным или последовательным соединением ветвей одной эквивалентной ветвью путем суммирования их токов или напряжений. Речь здесь идет о суммировании ординат или абсцисс заданных характеристик ветвей цепи. Этот метод особенно эффективен в случае цепи с одним источником: цепь представляется источником и одним эквивалентным нелинейным элементом.

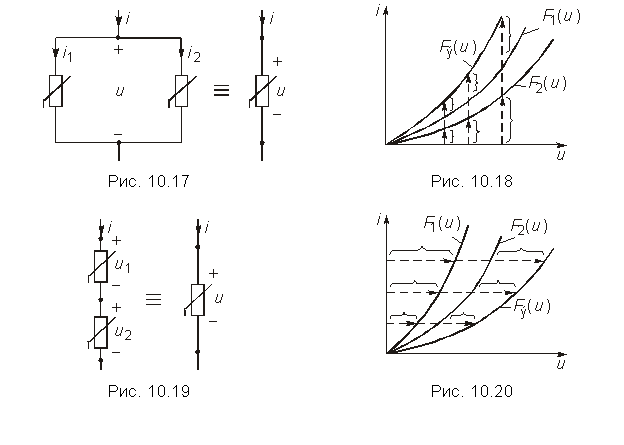
Пусть два НЭ с уравнениями (ВАХ) i₁ = F₁(u₁) и i₂ = F₂(u₂) включены параллельно (рис. 10.17).

Необходимо найти уравнение НЭ, эквивалентного данному соединению элементов. Так как элементы соединены параллельно, то u₁ = u₂ = u, а по первому закону Кирхгофа i = i₁ + i₂. Выполним сложение токов графически, как показано на рис. 10.18. Задаемся значением напряжения. При этом значении напряжения находим токи НЭ и суммируем их. Задаемся новым значением напряжения и опять суммируем токи. Таким образом, находим серию точек, соединяя которые, получаем ВАХ эквивалентного НЭ.

Рассмотрим последовательное соединение НЭ (рис. 10.19). В данном случае i₁ = i₂ =i, a u =u₁ + u₂. Процесс определения ВАХ НЭ показан на рис.10.20. Заметим, что рассмотренные преобразования применимы и в случае, когда последовательно или параллельно соединены несколько нелинейных, а также линейных элементов.

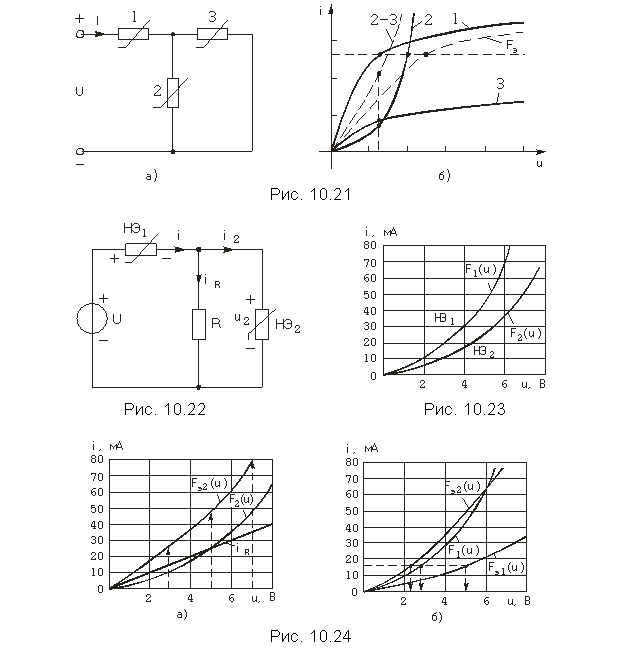
Пример. На рис. 10.21, а показана подключенная к источнику напряжения цепь из трех резистивных НЭ (рис. 10.21, б). Суммирование ординат характеристик элементов 2 и 3, соединенных параллельно, дает эквивалентную характеристику 2—3. Суммируя абсциссы последней с абсциссами кривой 1, получаем эквивалентную характеристику нелинейной цепи F_э. Из графиков рис. 10.21, б можно, задаваясь напряжением на входе, получить токи и напряжения ветвей.

Пример. Рассчитаем напряжения и токи в цепи, схема которой изображена на рис. 10.22, где U = 5 В, R = 500 Ом, а ВАХ НЭ заданы графиками на рис. 10.23.

Поскольку ВАХ заданы графиками, то при решении воспользуемся графическими построениями. Найдем ВАХ i = F_э2(u) двухполюсника, эквивалентного параллельному соединению линейного сопротивления R и НЭ₂. Для этого перенесен ВАХ НЭ₂ на новый рисунок и построим ВАХ линейного элемента (рис. 10.24, а). На этом же рисунке показана эквивалентная ВАХ i = F_э2(u). Перенесем эту эквивалентную ВАХ и ВАХ НЭ₁ на рис. 10.24, б и найдем ВАХ эквивалентного двухполюсника i = F_э1(u), который присоединяется к зажимам источника.

По рис. 10.24, б по кривой i = F_э1(u) находим, что напряжению u = 5 В соответствует ток i = 16 мА, по кривой i = F₁(u) – напряжение на НЭ₁ u₁ = = 2,8 B и по кривой i = F_э2(u) – напряжение на параллельном соединении R и НЭ₂ u₂ = 2,2 В. Зная это напряжение, по графикам рис. 10.24, а находим i_R = 11 мА и i₂ = 5 мА.

10.5. Аналитическое представление вольт-амперных характеристик

Часто необходимо иметь аналитические выражения для вольт-амперных характеристик нелинейных элементов. Эти выражения могут лишь приближенно представлять ВАХ, поскольку физические закономерности, которым подчиняются зависимости между напряжениями и токами в электронных и полупроводниковых приборах, не выражаются аналитически.

Задача приближенного аналитического представления функции, заданной графически или таблицей значений, в заданных пределах изменения ее аргумента (независимой переменной) предполагает, во-первых, выбор аппроксимирующей функции, т. е. функции, с помощью которой приближенно представляется заданная зависимость, и, во-вторых, выбор критерия оценки «близости» этой зависимости и аппроксимирующей ее функция.

В качестве аппроксимирующих функций используются, чаще всего, алгебраические полиномы, некоторые дробные рациональные и трансцендентные функции или совокупность отрезков прямых линий.

Будем считать, что ВАХ нелинейного элемента i = F(u) задана графически, т. е. определена в каждой точке интервала U_min u  U_max, и представляет собой однозначную непрерывную функцию переменной u. Тогда задача аналитического представления вольт-амперной характеристики может рассматриваться как задача аппроксимации заданной функции x(x) выбранной аппроксимирующей функцией f(x).

О близости аппроксимирующей f(x) и аппроксимируемой x(x) функций или, иными словами, о погрешности аппроксимации, обычно судят по наибольшему абсолютному значению разности между этими функциями в интервале аппроксимации а х b, т. е. по величине

Часто критерием близости выбирается среднее квадратическое значение разности между указанными функциями в интервале аппроксимации, т. е. величина

.

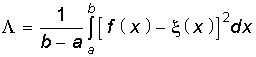Иногда под близостью двух функций f(x) и x(x) понимают совпадение в заданной точке x = X₀ самих функций и n + 1 их производных.

Наиболее распространенным способом приближения аналитической функции к заданной является интерполяция (метод выбранных точек), когда добиваются совпадения функций f(x) и x(x) в выбранных точках (узлах интерполяции) х_k, k = 0, 1, 2, ..., n.

Погрешность аппроксимации может быть достигнута тем меньшей, чем больше число варьируемых параметров входит в аппроксимирующую функцию, т. е., например, чем выше степень аппроксимирующего полинома или чем больше число отрезков прямых содержит аппроксимирующая линейно-ломаная функция. Одновременно с этим, естественно, растет объем вычислений как при решении задачи аппроксимации, так и при последующем анализе нелинейной цепи. Простота этого анализа наряду с особенностями аппроксимируемой функции в пределах интервала аппроксимации служит одним из важнейших критериев при выборе типа аппроксимирующей функции.

В задачах аппроксимации вольт-амперных характеристик электронных и полупроводниковых приборов стремиться к высокой точности их воспроизведения, как правило, нет необходимости ввиду значительного разброса характеристик приборов от образца к образцу и существенного влияния на них дестабилизирующих факторов, например, температуры в полупроводниковых приборах. В большинстве случаев достаточно «правильно» воспроизвести общий усредненный характер зависимости i = F(u) в пределах ее рабочего интервала.

Полиномиальная аппроксимация

В качестве аппроксимирующей функции в задачах аналитического представления вольт-амперных характеристик очень часто используются алгебраические полиномы

той или иной степени.

Постоянные представляют собой варьируемые параметры, значения которых выбираются такими, чтобы в интервале аппроксимации a x b свести к минимуму погрешность аппроксимации в соответствии с выбранным критерием близости.

В простейшем случае критерием близости может служить совпадение значений аппроксимирующей и аппроксимируемой функций в возможно большем числе выбранных точек, расположенных в интервале аппроксимации. Соответствующий метод приближенного воспроизведения функций носит, как мы уже упоминали, название интерполирования, а дискретные точки, в которых требуется точное совпадение функций f(x) и x(x), называются узлами интерполирования. Их число на единицу превышает степень интерполирующего полинома. Действительно, записывая равенство функций f(x_k) = x(x_k) в каждом из узлов интерполирования x_k, k = 0, 1, 2, ..., n, получим систему из n + 1 линейных уравнений

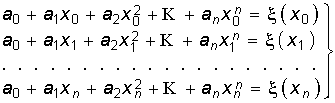
с таким же числом неизвестных коэффициентов интерполирующего полинома.

В теории интерполирования функций доказывается, что система уравнений (10.6) имеет единственное решение. Единственным, следовательно, будет и решение рассматриваемой задачи интерполирования вольт-амперной характеристики полиномом выбранной степени.

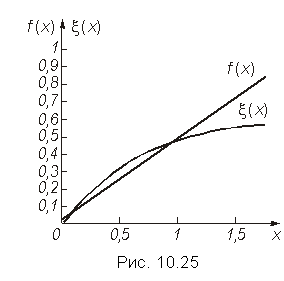
Приведем простейший пример интерполирования в интервале 0  x 1,5 полиномом первой степени функции , заданной аналитически. Расположим узлы интерполирования, а их должно быть n + 1 = 2, при x₀ = 0,1 и x₁ = 1,0. Тогда система уравнений относительно искомых коэффициентов a₀ и a₁ будет такой: и . Из ее решения следует а₀ = 0,036, a₁ = 0,597 и f(x) = 0,036 + 0,597x. Графики функций f(x) и x(х) приведены на рис. 10.25. Они показывают, что точность воспроизведения заданной функции невелика. В заданном интервале 0  x 1,5 наибольшая погрешность |f(x)—x(х)|, т. е. max|f(x)—x(х)| находится на одной из границ интервала при х = = 1,5 и составляет 0,158. Ее можно уменьшить, выбрав другие узлы интерполирования и, тем более, повысив степень интерполирующего полинома. Так, графики той же функции и интерполирующего полинома второй степени с узлами интерполирования x₀ = 0,15, x₁ = 0,6 и x₂ = 1,2 практически совпадают. На рис. 10.26 приведен график разности этих функций, из которого следует, что погрешность в том же заданном интервале не превышает 0,026, т. е. уменьшилась по сравнению с линейной интерполяцией в 6 раз.

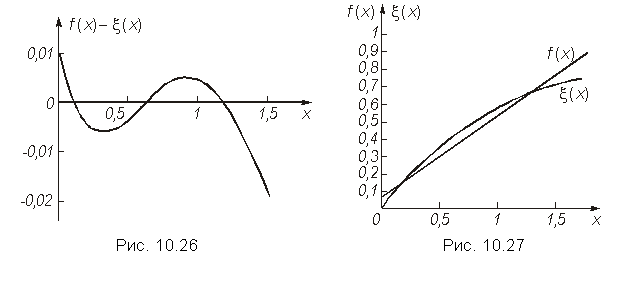
Одним из эффективных методов аппроксимации функций, в котором погрешность аппроксимации контролируется во всем интервале приближения а Ô x Ô b, а не в его дискретных точках, является метод наилучшего равномерного приближения (аппроксимации) функций (приближения по П.Л. Чебышеву). В этом методе параметры аппроксимирующей функции выбираются такими, чтобы в интервале приближения наибольшее по абсолютной величине отклонение функции f(x) от непрерывной функции x(х) было бы минимально возможным, или, используя обозначения (10.3), чтобы в интервале а Ô х Ô b

.

В рассмотренном выше примере этому критерию удовлетворяет полином f(х) = 0,071 + 0,518х. Наибольшие его отклонения от функции в интервале 0 Ô x Ô 1,5 расположены при x = 0, х =x_m = 0,658 и х = 1,5 (см. рис. 10.27), причем, что очень важно, все они равны по абсолютной величине. Легко понять, что любое изменение наклона (а₁) или уровня (а₀) полинома f(x), которое ведет к уменьшению экстремального отклонения в двух из трех указанных точек, увеличивает отклонения в оставшейся точке. Таким образом, полином f(x) = 0,071 + 0,518х из всех полиномов первой степени действительно минимизирует абсолютную величину отклонения от функции 1—e^–x в интервале 0 Ô x Ô 1,5.

В теории аппроксимации функций доказывается, что наибольшее по абсолютной величине отклонение полинома f(х) степени п от непрерывной функции x(x) будет минимально возможным, если в интервале приближения а Ô х Ô b разность f(х)—x(x) не меньше, чем п + 2 раза принимает свои последовательно чередующиеся предельные наибольшие f(х)—x(x) = = L > 0 и наименьшие f(х)—x(x) = = –L значения (критерий Чебышева).

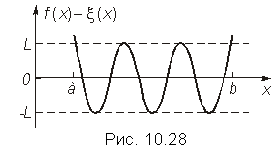
Характер графика разности f(х)—x(x) для полинома f(х) пятой степени, удовлетворяющего этому критерию, приведен на рис. 10.28. Этому же критерию удовлетворяет полином f(х) в рассмотренном выше примере (см. рис. 10.27).

Во многих прикладных задачах находит применение полиномиальная аппроксимация по среднеквадратическому критерию близости, когда параметры аппроксимирующей функции f(х) выбираются из условия обращения в минимум в интервале аппроксимации а Ô х Ô b квадрата отклонения функции f(х) от заданной непрерывной функции x(х), т. е., из условия:

.

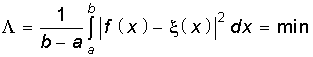В соответствии с правилами отыскания экстремумов решение задачи сводится к решению системы линейных уравнении, которая образуется в результате приравнивания к нулю первых частных производных функции L по каждому из искомых коэффициентов а_k аппроксимирующего полинома f(x), т. е. уравнений

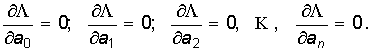
Доказано, что и эта система уравнений имеет единственное решение. В простейших случаях оно находится аналитически, а в общем случае – численно. Так, в рассматриваемом примере система уравнений при аппроксимации в интервале 0 Ô x Ô l,5 функции 1- e^-x полиномом первой степени такова:

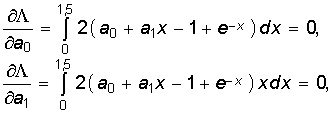
или после преобразований:

Поэтому f(х) = 0,108 + 0,500x.

Заметим, что, как правило, средняя квадратическая погрешность наилучшего равномерного приближения функций f(х) и x(х) лишь не намного отличается от минимально возможной. Обратное утверждение обычно ошибочно, т. е. при квадратической аппроксимации в некоторых участках интервала аппроксимации возможны существенные превышения погрешности аппроксимации (выбросы) по сравнению с теми, которые соответствуют критерию (10.7).

Вернемся к вольт-амперным характеристикам. Общий вид записи степенного полинома, аппроксимирующего ВАХ:

Иногда бывает удобно решать задачу аппроксимации заданной характеристики в окрестности рабочей точки U₀. Тогда используют степенной полином другого вида:

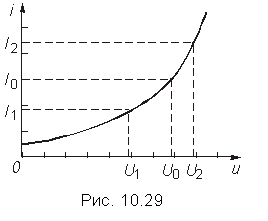
Пример. Используя метод интерполяции, аппроксимировать ВАХ нелинейного резистивного элемента (рис. 10.29) степенным полиномом. Аппроксимированная ВАХ должна совпадать с заданной в выбранных точках U₀, U₁ и U₂.

Составим систему уравнений:

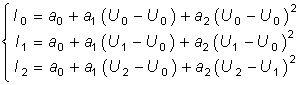
из которой найдём искомые коэффициенты

Пример. ВАХ нелинейного резистивного элемента i =F(u) задана таблицей:

Используя квадратический критерий, аппроксимировать характеристику выражением .

Сумма квадратов отклонений аппроксимирующей функции от заданной: минимальна при значении коэффициента a₂, удовлетворяющего уравнению

, откуда .

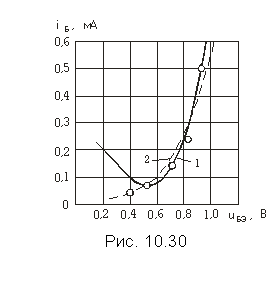
Пример. На рис. 10.30 кружочками показаны полученные экспериментально пять точек характеристики транзистора КТ301. Осуществим степенную аппроксимацию этой характеристики в диапазоне от 0,4 до 0,9 В полиномом второй степени в окрестности рабочей точки U₀ = 0,7 В.

Коэффициенты полинома найдем, используя метод интерполяции. Выберем в качестве узлов интерполяции точки, соответствующие напряжениям 0,5; 0,7 и 0,9 В и составим систему уравнений:

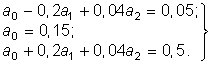
Решение этой системы дает a₀ = 0,15 мА, a₁ = 1,125 мА/В, a₂ = = 3,125 мА/В². Кривая тока

проходит через три экспериментальные точки, соответствующие узлам интерполяции (см. рис. 10.30, кривая 1). Из рисунка видно, что некоторые экспериментальные точки (например, при U_БЭ = 0,4 В) плохо «ложатся» на эту кривую. Кроме того, появляется загиб в нижней части характеристики.

Лучшей аппроксимации можно добиться, если использовать полином четвертой степени и выбрать соответственно пять узлов интерполяции (0,4; 0,5; 0,7; 0,8; 0,9 В). В этом случае кривая тока i_Б пройдет через все пять экспериментальных точек.

Однако можно попытаться сохранить вторую степень полинома и улучшить аппроксимацию, воспользовавшись каким-либо другим методом для определения коэффициентов a_s. Найдем эти коэффициенты, используя среднеквадратическое приближение тока по всем пяти экспериментальным значениям.

Составим уравнения (10.9):

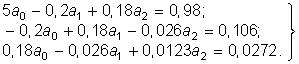
Решение этой системы уравнений дает: a₀ = 0,164 мА, a₁ = l,07 мА/В и a₂ = = 2,069 мА/В².

График тока при этом определяется полиномом

и показан на рис. 10.30, кривая 2. Эта характеристика является более приемлемой для аналитического описания экспериментальных результатов.

Кусочно-линейная аппроксимация

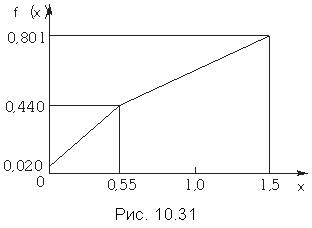
Наряду с полиномиальной аппроксимацией ВАХ в радиотехнике и связи широко используется их аппроксимация линейно-ломаной зависимостью – совокупностью отрезков прямых, образующих в интервале аппроксимации непрерывную функциюf(x). Так, на рис. 10.31 приведена линейно-ломаная зависимость

составленная из двух отрезков прямых и аппроксимирующая в интервале 0 Ô x Ô 1,5 функцию 1—e^-x с абсолютной погрешностью, не превышающей 0,024.

Параметры аппроксимирующих прямых могут быть выбраны так, чтобы в интервале аппроксимации выполнялся критерий (10.7) или (10.8).

В пределах каждого из линеаризированных участков вольт-амперной характеристики применимы все методы анализа колебаний в линейных электрических цепях. Ясно, что, чем на большее число линеаризированных участков разбивается заданная вольт-амперная характеристика, тем точнее она может быть аппроксимирована и тем больше объем вычислений в ходе анализа колебаний в цепи.

Во многих прикладных задачах анализа колебаний в нелинейных резистивных цепях аппроксимируемая вольт-амперная характеристика в интервале аппроксимации с достаточной точностью представляется двумя или тремя отрезками прямых. Графики типичных аппроксимирующих функций приведены на рис. 10.32, а – в, где U_отс – так называемое напряжение отсечки, U_н и I_н – напряжение и ток насыщения в НЭ.

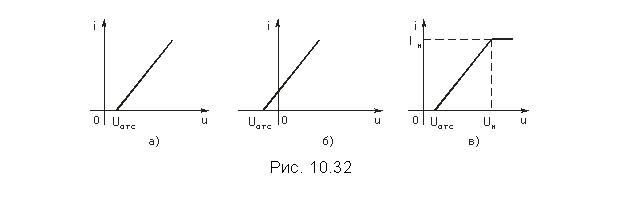
Подобная аппроксимация вольт-амперных характеристик дает в большинстве случаев вполне удовлетворительные по точности результаты анализа колебаний в нелинейной резистивной цепи при «больших» по величине воздействиях на нелинейный элемент, т. е. когда мгновенные значения токов в нелинейном элементе изменяются в предельно допустимых границах от I = 0 до I = I_н (см. рис. 10.32, в).

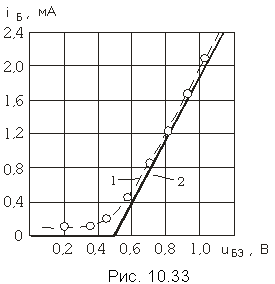
Пример. На рис. 10.33 (кривая 1) приведен график экспериментальной зависимости транзистора КТ306. Выполним кусочно-линейную аппроксимацию этой зависимости.

Используя полином первой степени

осуществим аппроксимацию заданной зависимости в окрестности точки U₀ = = 0,8 В и определим коэффициенты по методу Тейлора:

Ток в рабочей точке в соответствии с экспериментальными данными I₀ = = 1,2 мА. Крутизну S(U₀) в рабочей точке можно найти приближенно методом приращений:

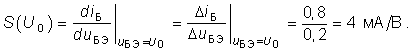
В результате аппроксимации получим

Видно, что при u_БЭ < 0,5 В ток i_Б принимает отрицательные значения, что не согласуется с экспериментальной зависимостью. Таким образом, полученным полиномом будем аппроксимировать заданную зависимость на участке u_БЭ > 0,5. На участке же 0 < u_БЭ < 0,5 можно выбрать полином первой степени с нулевыми коэффициентами, т. е. i_Б = 0. Итак, аппроксимирующая функция запишется в виде (рис. 10.33, кривая 2)

Представим эту зависимость в более общей форме:

Другие виды аппроксимации вольт-амперных характеристик

Вольт-амперная характеристика идеализированного полупроводникового диода совпадает с характеристикой идеализированного р-п перехода

где I₀ - обратный (тепловой) ток, j_T - тепловой потенциал (j_T @ @ 0,026 В при T = 300К).

Функция (10.12) иногда используется для аппроксимации вольт-амперных характеристик. Ее единственным варьируемым параметром является обратный ток I₀, значение которого можно найти, интерполируя заданную характеристику функцией (10.12) в одной из точек. График функции (10.12) подобен приведенному на рис. 10.1, а.

Заметим, что вольт-амперные характеристики реальных полупроводниковых диодов в силу ряда причин отличаются от идеализированных и чаще всего аппроксимируются отрезками прямых.

В ряде случаев вольт-амперные характеристики, подобные приведенной на рис. 10.32, в, аппроксимируются функцией

с тремя варьируемыми параметрами I₀, g и U₀.

Можно считать, что I = I_н, U₀ - соответствует значению напряжения U, при котором i = 0,5I_max, а постоянная g находится по известной крутизне S = dI/dU аппроксимируемой вольт-амперной характеристики в точке U₀ из условия S(U₀) = 0,5I₀.

10.6. Аналитические методы расчета нелинейных резистивных цепей

Составление уравнений состояния цепи на основании законов Кирхгофа

Из предыдущих разделов известно, что в общем случае, когда цепь содержит n_в ветвей (в том числе n_т источников тока) и n_у-узлов, число неизвестных токов (напряжений) равно n_в – n_у + 1 – n_т. Для отыскания такого числа неизвестных составляется система уравнений по законам Кирхгофа.

По первому закону Кирхгофа (ЗТК) записывается n_у – 1 уравнений вида (1.16):

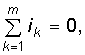
где m – число ветвей, сходящихся в узле.

По второму закону Кирхгофа (ЗНК) записывается n_в – n_у + 1 уравнений вида (1.17):

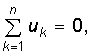
где п—число ветвей, входящих в контур.

Если цепь содержит, кроме линейных, также и НЭ, то в системе уравнений, описывающей состояние цепи, появятся уравнения вида i_k = F_k(u_k). Методика составления уравнений состояния цепи на основе законов Кирхгофа остается такой же, как и в случае линейных резистивных цепей.

Составим, например, систему уравнений состояния для цепи, схема которой изображена на рис. 10.13. Пусть ВАХ нелинейного элемента аппроксимируется выражением

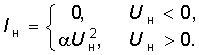
Зададимся положительными направлениями напряжений и токов. Цепь содержит один независимый контур (I) и один независимый узел (1). Уравнения, записанные по ЗТК и ЗНК, имеют следующий вид:

К этим уравнениям дописываем уравнение (10.14). Неизвестными в данной системе уравнений являются напряжение U_н и токи I₁ и I_н. Всего три неизвестных. Для их отыскания составлено три уравнения. Как видим, процесс составления системы уравнений такой же, как и в случае линейной цепи. Однако процесс решения полученной системы, которая содержит нелинейное уравнение, может существенно затрудниться. Для большинства относительно сложных цепей аналитического решения системы уравнений может и не существовать. Тогда приходится прибегать к численным методам решения.

В рассматриваемом примере достаточно просто получить аналитическое решение. Предположим вначале, что решение системы уравнений существует при U_н > 0. Тогда уравнение НЭ имеет вид

Выразим из уравнения (10.15) ток I₁ = I_н – J₀₂ и подставим его в уравнение (10.16). В результате этой операции получим

Подставив в (10.18) выражение (10.17), получим уравнение относительно неизвестного напряжения на нелинейном двухполюснике

Отсюда имеем

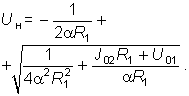
Пусть R₁ = l кОм, U₀₁ = 14 В, J₀₂ = 10 мА, a = 10^–5 А/В. Тогда U_н = 20 В.

Второе решение уравнения (10.19) даст U_н < 0. Это решение не подходит, так как применялось уравнение НЭ, справедливое при U_н > 0.

Допустим теперь существование решения системы уравнений (10.15)— (10.16) при U_н< 0. Согласно уравнению НЭ (10.14) I_н = 0. Тогда из уравнения (10.18) имеем

а это противоречит условию, что U_н< 0.

Таким образом, остается первое решение (10.20). Найдем остальные неизвестные. Из (10.17) имеем , а из (10.15) I₁ = I_н –J₀₂ = —6 мА.

В данном примере получено аналитическое решение системы нелинейных уравнений. Если бы ВАХ нелинейного элемента описывалась более сложной функцией, то этого достичь не удалось бы.

Составление уравнений состояния цепи методом узловых напряжений (потенциалов)

Как известно, переменными в методе узловых напряжений являются напряжения n_у – 1 узлов по отношению к базисному узлу.

Рассмотрим в качестве примера схему, изображенную на рис. 10.34. Пусть ВАХ нелинейных элементов описываются выражениями I = aU³ для элемента НЭ₁ и I = bU² для элемента НЭ₂. В схеме имеется зависимый источник (ИТУТ) с током I₅ = H_iI₁.

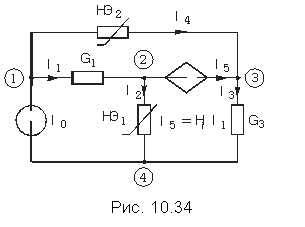
Приняв узел 4 за базисный, имеем три независимых узла: 1, 2 и 3. Токи ветвей выражаются через узловые напряжения U₁, U₂ и U₃ следующим образом:

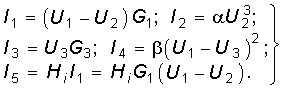
Составим уравнения для узлов 1, 2 и 3 по ЗТК:

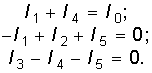
Подставив в эти уравнения значения токов из (10.21), получим

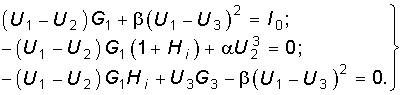
Уравнения узловых напряжений получены в виде системы трех нелинейных уравнений с тремя неизвестными узловыми напряжениями. Можно уменьшить число уравнений, если из первого уравнения выразить U₂ через U₁ и U₃ и исключить его из двух остальных уравнений. В результате получим систему двух нелинейных уравнений с двумя неизвестными напряжениями узлов 1 и 3.

Решить данную систему уравнений можно одним из численных методов (например, известным из математики методом Ньютона— Рафсона). Определив узловые напряжения, можно вычислить токи и напряжения ветвей.

Аналитические методы нахождения рабочей точки

Задача о нахождении рабочей точки может решаться и аналитическими методами, если зависимость I(U) нелинейного резистивного элемента задана аналитически. Она сводится к решению нелинейного уравнения

относительно напряжения U =U₀ в рабочей точке резистора. Так например, в цепи с идеализированным выпрямительным диодом, у которого , где I₀ и ^j_T – некоторые постоянные, задача нахождения рабочей точки приводит к решению трансцендентного уравнения относительно неизвестного напряжения U= U₀ с последующим нахождением тока I₀ = (Е—U₀)/R в рабочей точке диода.

Если вольт-амперная характеристика нелинейного резистора аппроксимирована полиномом I= a₁U + a₂U² + ... + a_nUⁿ, то уравнение (10.23) будет представлять собой алгебраическое уравнение степени п относительно искомого напряжения в рабочей точке и, как известно, в общем случае может быть решено лишь численно, если n> 4.

В заключение следует подчеркнуть, что нелинейный характер взаимозависимостей между реакциями и воздействием в анализируемых цепях обусловливает неприменимость к ним в общем случае принципа наложения, лежащего в основе высокоэффективных методов анализа и синтеза линейных электрических цепей. По этой же причине только в редких случаях удается найти решение задач анализа колебаний в аналитической форме, даже в таких простейших нелинейных цепях, как нелинейные резистивные цепи.

10.7. Стабилизация постоянного напряжения нелинейными резистивными цепями

Для поддержания постоянства (стабилизации) напряжения питания активных электрических цепей при возможных колебаниях первичного питающего напряжения и изменениях сопротивления нагрузки используются устройства, получившие название стабилизаторов постоянного напряжения.

Схема простейшего стабилизатора приведена на рис. 10.35, а. В него входят генератор первичного питающего напряжения, задающее напряжение U_г которого под воздействием дестабилизирующих факторов может меняться относительно его среднего значения, и стабилитрон, подсоединенный параллельно нагрузке. Его вольт-амперная характеристика была приведена на рис. 10.1, б. Внутреннее сопротивление генератора R_г и сопротивление нагрузки R_н считаются чисто резистивными.

При анализе работы стабилизатора цепь, внешнюю по отношению к стабилитрону, заменим эквивалентным генератором с задающим напряжением U₀ и внутренним сопротивлением R₀. После этой замены схема анализируемой цепи преобразуется в схему рис. 10.35, б. На этой схеме через U_н обозначено напряжение на зажимах нагрузки, которое совпадает с напряжением в рабочей точке стабилитрона (рис. 10.35, а). Зная последнюю, можно найти токи в ветвях исходной цепи: I_г = (U_г—U_н)/R_г, I_н = U_н/R_н, I_д = = I_г—I_н.

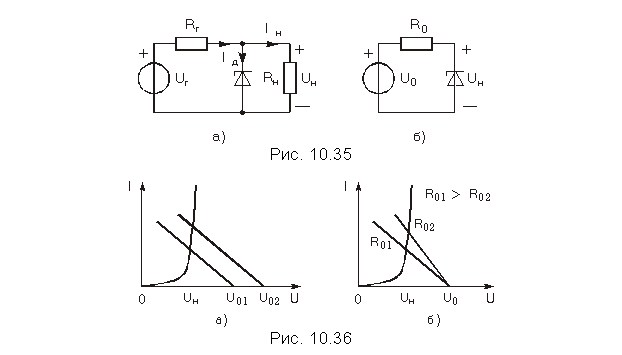
Рис. 10.36, а и б показывает, что рабочая точка стабилитрона изменяется вдоль прямой, практически параллельной оси ординат, с изменением как задающего напряжения эквивалентного генератора (рис. 10.36, а), так и его внутреннего сопротивления (рис. 10.36, б). Тем самым решается задача стабилизации напряжения на зажимах нагрузки, поскольку оно незначительно меняется при изменении в широких пределах первичного питающего напряжения U_г и сопротивления нагрузки R_н.

Естественно, что эффект стабилизации достигается ценой рассеяния энергии в стабилитроне и резисторе R_г.

10.8. Вопросы и задания для самопроверки

1. Какими уравнениями описываются нелинейные резистивные цепи, какими – нелинейные цепи, содержащие реактивные элементы? 2. Какие значения может принимать дифференциальное сопротивление нелинейного элемента? 3. Какой элемент цепи обладает одинаковыми статическим и дифференциальным сопротивлением? 4. Что называется рабочей точкой вольт-амперной характеристики нелинейного элемента? 5. Приведите пример многозначной вольт-амперной характеристики нелинейного элемента? 6. Объясните на примерах трехзначных характеристик N-типа и S-типа возможность получения неоднозначного решения задачи нахождения рабочей точки вольт-амперной характеристики резистивных нелинейных элементов? 7. В каком режиме (постоянного или переменного тока) могут быть сняты статические вольт-амперные характеристики резистивных нелинейных элементов? 8. Нарисуйте схему измерительной установки для снятия статической вольт-амперной характеристики резистивного двухполюсника. 9. Применим ли метод эквивалентного генератора к нелинейной цепи? К ее линейной части? Как определяются характеристики этого генератора? 10. Какие из указанных ниже законов справедливы для нелинейной цепи (нелинейного элемента): закон Ома, закон Кирхгофа, закон Джоуля-Ленца? 11. В чем отличие метода эквивалентных преобразований для линейной и нелинейной цепей? 12. Найдите ток i₂ и напряжение u₂ на нелинейном элементе (рис. 10.37), если U₀ = 6 В, I₀ = 3 А, R₁ = 8 Ом, R₂ = 6 Ом, R₃ = 3 Ом, i = 0,1u² А. Ответ: i₂ = 1,6 А, u₂ = 4 В. 13.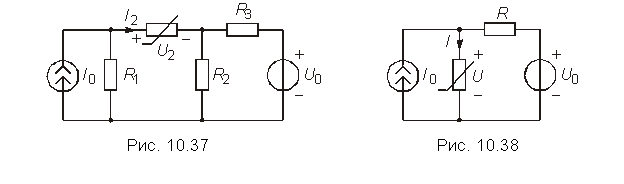
Найдите токи и напряжения в ветвях цепи (рис. 10.38), если U₀ = 6 В, I_А = 6 мА, R = 1 кОм, i = 0,001u² А. Найдите алгебраические суммы частичных токов и напряжений, вызванных действием каждого источника в отдельности и убедитесь, что метод наложения дает неверные результаты. Ответ: I = 9 мА, U = 3 В. Ток и напряжение, вызванные генератором тока I^I = 4 мА, U^I = 2 В; ток и напряжение, вызванные генератором напряжения, имеют те же значения I^II = 4 мА, U^II = 2 В. В результате получаем

I = I^I + I^II = 8 мА,

U = U^I + U^II = 4 В. Cледовательно, принцип наложения для нелинейной цепи не справедлив. 14. Найдите токи и напряжения в цепи (рис. 10.39), если I₀ = 0,2 А, R₁ = 100 Ом, i = 0,01u² А и определите соответствующие значения статических и дифференциальных сопротивлений нелинейного элемента и параллельного соединения сопротивления R₁ и нелинейного элемента. Ответ: I = 0,16 А, I₁ = 0,04 А, R_ст = 25 Ом, R_{ст экв} = 20 Ом, R_д = 12,5 Ом, R_{д экв} = 11,1 Ом. 15. Найдите ток и напряжение в цепи (рис. 10.40), если u = i² В, U₀ = 11 В, R₁ = 10 Ом. Определите новое значение R₁, при котором дифференциальное сопротивление в новой рабочей точке вольт-амперной характеристики нелинейного элемента будет равно 1 Ом.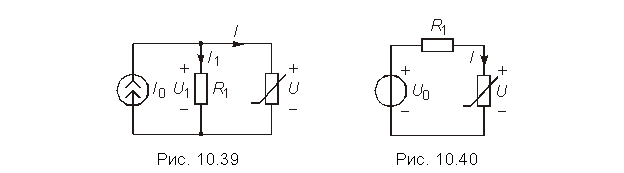
Ответ: I = 1 А, U₁ = 10 В, R₁ = 21,5 Ом. 16.
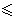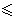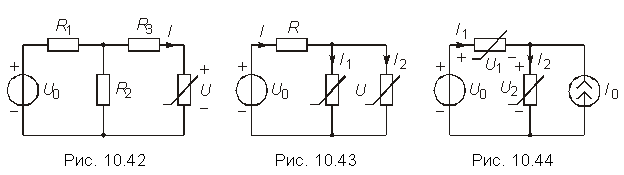
На рис.10.41 изображена вольт-амперная характеристика стабилитрона – нелинейного полупроводникового прибора, используемого для стабилизации постоянного напряжения на входе питаемой цепи. Найдите, в каких пределах может изменяться сопротивление нагрузки R_н при неизменном напряжении U_н = 6 В, если U₀ = 12 В, R = 100 Ом, U = 6 В, I_max = = 50 мА, I_min = 10 мА. Ответ: 120 Ом R_н 600 Ом. 17. Найдите величину сопротивления R₃ (рис. 10.42), при которой I = 3 мА, если U₀ = 16 В, R₁ = R₂ = 2 кОм, I = (2^U – 1)×10^-3 А. Определите в рабочей точке дифференциальное и статическое сопротивление нелинейного элемента. Ответ: R₃ = 1 кОм, R_ст = 666,7 Ом, R_д = 364 Ом. 18. Найдите вольт-амперную характеристику параллельного соединения НЭ (рис. 10.43), если i₁ = 0,02u² А, i₂ = 0,08u² А. Определите величину R, при которой i = 0,4А, если u₀ = 6В. Ответ: R = 10 Ом. 19. Найдите токи и напряжения в цепи (рис. 10.44), если U₀ = 30 В, I₀ = 3 А, u₁ = В, i₂ = 0,01u₂² В. Ответ: i₁ = 1 А, u₁ = 10 В, i₂ = 4 А, u₂ = 20 В. 20. Найдите токи и напряжения в цепи (рис. 10.45), если U₀₁ = = U₀₂ = 6 В, u₁ = В, u₂ = В, R = 0,8 Ом.

Ответ: I₁ = 1 А, I₂ = 4 А, I₃ = 5 А, U₁ = U₂ = 2В, U_R = 4 В.

21.
Применив интерполяционный метод, аппроксимируйте ВАХ нелинейного резистивного элемента (рис. 10.45) полиномом вида .

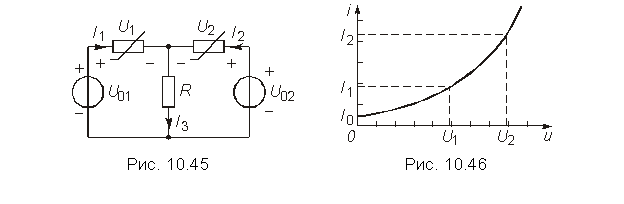
Ответ: a₀ = i₀; ;

;

. 22. Заданную в виде таблицы (U_k, I_k) ВАХ нелинейного резистивного элемента аппроксимируйте линейной функцией .  

Uk	0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8
Ik	0	0.26	0.54	0.72	0.93	1.1	1.18	1.28	1.36

Коэффициент а₁ определить методом наименьших квадратов. Ответ: i = 1,94u. 23. Падающий участок ВАХ нелинейного резистивного элемента i = F(u) задан таблицей:

Uk	0.2	0.25	0.3	0.35	0.4
Ik	9.0	6.75	4.6	3.0	2.0

Аппроксимируйте характеристику на отрезке [0.2; 0.4] линейной функцией методом наименьших квадратов. Ответ: i = -35,3 + 15,7u.