Пусть критерий оптимизации задан функцией двух переменных

.

Надо проанализировать этот критерий на предмет нахождения оптимальных значений независимых переменных. Сделать это быстро можно с помощью таблицы подстановки с двумя переменными.

Сначала надо выделить для переменных х и у ячейки, например, х будет в ячейке А2, у – в ячейке В2.

Затем, в какую-либо ячейку ввести формулу для вычисления функции. Например, в ячейку С2.

После этого надо выбрать значения переменных, для которых необходимо проанализировать значения функции. Пусть это будут значения 1,5, 2, 2,5, 3, 3,5 для х и 0 0,1 0,2 0,3 0,4 для у.

Выбрать какую-нибудь ячейку, например, D6 и внести выбранные значения переменных в последовательные ячейки по строкам и по столбцам, начиная справа от D6 и вниз от D6. Пусть у нас значения х будут в строке 6, а значения у в столбце D.

В ячейку D6 внести формулу =С2.

Выделить массив ячеек D6:i11, т.е. тот массив, который должен быть заполнен данными вычисления по формуле.

Выполнить команду меню «Данные\Таблица подстановки».

В появившемся окошке надо заполнить два поля: «Подставлять значения по столбцам в:» и «Подставлять значения по строкам в:».

В нашем случае значения по столбцам представляют собой значения переменной х, поэтому эти значения надо подставлять в ту ячейку, которая и содержит значения переменной х, т.е. в ячейку А2. Значения по строкам представляют собой значения переменной у, поэтому их надо подставлять в ячейку В2. Указав адреса этих ячеек щелкнуть по ОК.

После этого получится таблица, содержащая значения критерия оптимизации, по которой уже можно судить о примерном положении искомого экстремума. Если это значение необходимо уточнить, то это делается простой заменой значений независимых переменных на новые, более точные.

Для наглядного представления поведения критерия оптимизации можно построить график этой функции, который представляет собой поверхность в трёхмерном пространстве. Для этого необходимо сделать следующее.

Выделить массив ячеек E7:I11, вызвать мастера диаграмм, выбрать тип диаграммы «Поверхность», вид – также «Поверхность» и по кнопке «Далее».

Чтобы на диаграмме по осям стояли значения переменных, а не абракадабра, необходимо сделать следующее. Перейти на закладку «Ряд». Выделить строчку «Ряд1», щелкнуть мышкой в поле «Имя», а затем щелкнуть по ячейке D7. Затем выделить строчку «Ряд2», щелкнуть мышкой в поле «Имя», а затем щелкнуть по ячейке D8. И так проделать со всеми рядами. После этого щелкнуть в поле «Подписи по оси Х» и выделить мышкой ячейки E6:i6. Затем щелкнуть по кнопке «Далее».

В появившемся окне можно задать подписи по осям, название диаграммы, параметры легенды.

Создание массивов и работа с ними

Массив это диапазон ячеек, рассматриваемый как единое целое или диапазон ячеек, над которыми надо произвести однотипную операцию.

Например, если стоит задача умножения числа на матрицу, то диапазон ячеек, в которых находятся элементы матрицы будет являться массивом.

В мастере функций в категориях «Математические» и «Ссылки и массивы» находятся специальные функции для работы с массивами.

Как правило, завершение ввода для формул, работающих с массивами, осуществляется нажатием сочетания клавиш Shift+Ctrl+Enter.

Сначала рассмотрим простейшие операции с массивами: сложение, вычитание, умножение, деление, возведение в степень.

Последовательность действий при работе с массивами:

• выделяется диапазон ячеек, в которых будет содержаться результат;
• делается щелчок в строке формул и набирается формула;
• завершается ввод формулы нажатием сочетания клавиш Shift+Ctrl+Enter.

Запись вышеперечисленных операций в формуле выглядит одинаково: после знака равенства указывается диапазон ячеек первого массива, затем знак операции и диапазон ячеек второго массива.

Например, если в ячейках диапазона А1:С3 содержится таблица чисел и нам надо все эти числа умножить на 5, то формула будет выглядеть так: =А1:С3*5. Ну, а если в ячейках диапазона А5:С7 имеется ещё одна таблица и надо сложить почленно эти две таблицы, то формула будет такая: =А1:С3+А5:С7.

Если мы хотим получить, например, синусы от чисел, находящихся в ячейках диапазона А1:С3, то надо набрать такую формулу: =SIN(А1:С3).

Рассмотрим специальные функции для работы с определителями и матрицами.

Для вычисления определителя существует функция МОПРЕД() у которой в качестве аргумента должен быть указан диапазон ячеек, содержащий элементы определителя. Эта функция возвращает только одно значение, поэтому завершение ввода для этой функции можно осуществить обычным образом.

Для работы с матрицами служат следующие функции:

МОБР() – вычисление обратной матрицы;

МУМНОЖ(диап1;диап2) – вычисление произведения двух матриц;

ТРАНСП() – транспонирование матрицы.

Эти функции возвращают диапазон значений и для завершения ввода надо обязательно использовать сочетание клавиш Shift+Ctrl+Enter. Кроме этого, перед вводом функции надо выделить диапазон ячеек, в которых будет помещён результат.

Например, пусть элементы матрицы находятся в ячейках А1:С3. Мы хотим вычислить обратную матрицу. Сначала необходимо выделить диапазон ячеек для обратной матрицы. Как известно, обратная матрица имеет ту же размерность, что и исходная, поэтому мы должны выделить 9 ячеек. Пусть это будут ячейки А5:С7.

После этого в мастере функций находим функцию МОБР(), указываем её аргументом диапазон ячеек А1:С3 и нажимаем Shift+Ctrl+Enter. В ячейках А5:С7 видим результат.

Если вы все-таки поторопились и нажали на ОК, а не Shift+Ctrl+Enter, то надо сразу после этого, пока ещё диапазон ячеек А5:С7 остаётся выделенным, щелкнуть в строке формул и нажать Shift+Ctrl+Enter.

Аналогично поступают и в случае использования функции ТРАНСП(). Надо только учесть, что при транспонировании строки и столбцы меняются местами.

Для умножения матриц служит функция МУМНОЖ() с двумя аргументами. В первом аргументе указывается массив ячеек матрицы, которую умножают, а во втором аргументе указывается массив ячеек матрицы, на которую умножают. В результате умножения получается матрица, у которой число строк равно числу строк первой матрицы, а число столбцов равно числу столбцов второй матрицы.

Например, если матрицу 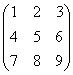умножить на матрицу , то получится матрица .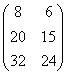

При работе с формулами, в которые входят массивы, надо помнить, что если диапазон ячеек под результат будет выделен неправильно, то данными заполнятся только выделенные ячейки, и никакого сообщения об ошибке не будет!

Формулы, которые возвращают массивы, в строке формул выглядят заключенными в фигурные скобки. Например, для приведённого выше примера вычисления обратной матрицы, в любой из ячеек диапазона А5:С7 можно увидеть одну и ту же формулу: {=МОБР(А1:С3)}.

Чтобы удалить такую формулу надо сначала выделить все ячейки, в которых она содержится, а затем нажать клавишу Delete.

Контрольные вопросы

1. Как организовать данные на листе для использования таблицы подстановки с двумя параметрами?

2. Что такое массив ячеек?

3. Как записывается формула, содержащая операции над массивом ячеек?

4. Как завершается ввод при наборе формулы для работы с массивом ячеек?

5. В чём заключается последовательность действий при работе с массивами?

6. Какие существуют встроенные функции для работы с массивами?

7. Как выглядит формула, содержащая массивы, в строке формул?

8. Как правильно удалить формулу с массивами?