9.10.1. Истоки решетчатого кодирования
9.10.3.1. Ошибочное событие и просвет
9.10.3.2. Эффективность кодирования
9.10.3.3. Эффективность кодирования для схемы 8-PSK при использовании решетки с четырьмя состояниями
9.10.4. Другие решетчатые коды
При использовании в системах связи реального времени кодов коррекции ошибок, описанных в главах 6—8, достоверность передачи улучшается за счет расширения полосы частот. Как для блочных, так и для сверточных кодов преобразование каждого n-кортежа входных данных в более длинный n-кортеж кодового слова требует дополнительного расширения полосы пропускания. Вследствие этого в прошлом кодирование не было особенно популярно в узкополосных каналах (таких, как телефонные), в которых расширять полосу частот сигнала было нецелесообразно. Однако приблизительно с 1984 года возникает активный интерес к схемам, где модуляция объединяется с кодированием; такие схемы называются решетчатым кодированием (trellis-coded modulation — ТСМ). Эти схемы позволяют повысить достоверность передачи, не расширяя при этом полосу частот сигнала. Схемы ТСМ используют избыточную небинарную модуляцию плюс конечный автомат (кодер). Что такое "конечный автомат" (finite-state machine) и какой смысл имеют его состояния? Конечный автомат (или автомат с конечным числом состояний) — это общее название устройств, обладающих памятью о прошлых сигналах; прилагательное конечный подчеркивает то, что существует ограниченное число однозначных состояний, которые может принимать система. Какой смысл заложен в понятие состояние конечного автомата? В наиболее общем смысле, состояние состоит из минимального объема информации, который, совместно с текущими данными на входе, может предсказывать данные на выходе системы. Состояние несет информацию о прошлых событиях и ограниченном наборе возможных данных на выходе в будущем. Будущие состояния ограничиваются прошлыми состояниями.
Кодер ТСМ с конечным числом состояний для каждого символьного интервала из набора сигналов выбирает один, формируя, таким образом, передаваемую последовательность кодированных сигналов. Полученный зашумленный сигнал обнаруживается и декодируется детектором/декодером, работающим согласно принципу максимального правдоподобия на основе мягкой схемы принятия решений. В стандартных системах, включающих модуляцию и кодирование, обычно принято отдельно описывать и реализовать детектор и декодер. Однако в системах ТСМ эти функции должны рассматриваться совместно. Можно добиться эффективного кодирования, не жертвуя скоростью передачи данных или не увеличивая ни ширину полосы частот, ни мощность [6, 31]. Вначале может показаться, что это утверждение нарушает некоторые основные принципы компромисса между мощностью или шириной полосы частот и вероятностью ошибки. Отметим, что компромисс здесь все же присутствует, поскольку ТСМ позволяет достичь эффективности кодирования за счет усложнения декодера.
При решетчатом кодировании набор сигналов многоуровневой/фазовой модуляции комбинируется со схемой решетчатого кодирования. Термин "схема решетчатого кодирования" применим к любой кодовой системе, которая обладает памятью (конечный автомат), такой например, как сверточный код. Сигналы многоуровневой/фазовой модуляции имеют совокупности, содержащие множественные амплитуды, множественные фазы или комбинации этих амплитуд и фаз. Иными словами, набор сигналов ТСМ наилучшим образом представляется любым набором сигналов (более чем двоичным), векторное представление которого может быть отображено на плоскости, подобной показанной на рис. 9.16, а для сигналов QAM. Схема решетчатого кодирования — это схема, которую можно охарактеризовать (решетчатой) диаграммой состояния, подобной решетчатым диаграммам, описывающим сверточные коды. Отметим, что хотя сверточные коды, представленные в главе 7, линейны, в общем случае решетчатые коды линейными быть не обязаны. Эффективность кодирования можно получить с помощью блочных или решетчатых кодов, однако здесь будут рассматриваться только решетчатые коды, поскольку наличие алгоритма декодирования Витерби делает решетчатое кодирование простым и эффективным. Унгербоек (Ungerboeck) показал, что при наличии шума AWGN схема ТСМ довольно просто может дать суммарную эффективность кодирования порядка 3 дБ по сравнению с некодированной системой, а при увеличении сложности можно получить эффективность порядка 6 дБ.
9.10.1. Истоки решетчатого кодирования
При ТСМ канальное кодирование и модуляция осуществляются вместе; невозможно просто определить, где начинается одно и заканчивается другое. Что же могло натолкнуть на разработку ТСМ? Возможно, все началось с мысли о том, что "не все подмножества сигналов (в совокупности) имеют равные пространственные свойства". Другими словами, для неортогонального множества сигналов, такого как MPSK, антиподные сигналы будут иметь наилучшие пространственные характеристики с точки зрения различения сигналов, в то время как ближайшие соседние сигналы будут иметь относительно плохие пространственные характеристики. Возможно, изначально идея кодовой модуляции возникла именно при попытке использовать эти различия.
Понять общие задачи ТСМ может помочь простая аналогия. Пусть в передатчике есть всезнающий волшебник. Как только биты сообщения попадают в систему, волшебник обнаруживает, что некоторые биты наиболее уязвимы к искажению, вызываемому каналом; следовательно, им присваиваются модулирующие сигналы, имеющие наилучшие пространственные характеристики. Подобным образом другие биты признаются весьма устойчивыми, поэтому они передаются с использованием сигналов с худшими пространственными характеристиками. Модуляция и кодирование осуществляются одновременно. Волшебник присваивает сигналы битам (модуляция), однако присвоение выполняется согласно критерию лучших или худших пространственных характеристик (канальное кодирование).
9.10.1.1. Увеличение избыточности сигнала
Схему ТСМ можно реализовать с помощью сверточного кодера, где k текущих битов и К-1 предыдущих битов используются для получения n=k+p кодовых битов, где К — длина кодового ограничения кодера (см. главу 7), а р — число битов четности. Отметим, что кодирование увеличивает размер множества сигнала с 2k до 2k+p. Унгербоек [31] исследовал повышение пропускной способности, достигаемое благодаря увеличению набора сигналов, и пришел к заключению, что максимальную эффективность кодирования при обычной многоуровневой модуляции без кодирования можно реализовать, удваивая передаваемый некодированный набор (р=1). Этого можно достичь путем кодирования со степенью kl(k+1) с последующим отображением групп из (k+ 1) бит в набор из 2k+1 сигналов. На рис. 9.21, а показан набор сигналов, модулированных 4-РАМ, до и после кодирования кодом со степенью кодирования 2/3 (после кодирования получаются 8-ричные сигналы РАМ). Аналогично на рис. 9.21, б показан набор сигналов с 4-ричной модуляцией PSK (QPSK) до и после перекодирования кодом со степенью кодирования 2/3 в 8-ричные сигналы PSK. Подобным образом на рис. 9.21, в показаны некодированные 16-ричные сигналы QAM до и после перекодирования кодом со степенью кодирования 4/5 в 32-ричные сигналы QAM. В каждом из случаев, показанных на рис. 9.21, система сконфигурирована таким образом, чтобы до и после кодирования средняя мощность сигнала была одинаковой. Кроме того, для обеспечения необходимой избыточности при кодировании размер набора сигналов увеличивается с M = 2k до M'=2k+1. Таким образом, М'=2М; однако увеличение размера алфавита не приводит к увеличению требуемой ширины полосы частот. Напомним из раздела 9.7.2, что ширина полосы пропускания при неортогональной передаче сигнала не зависит от плотности точек сигналов в совокупности; она зависит только от скорости передачи сигнала. Расширенный набор сигнала приводит к уменьшению расстояния между соседними точками символов (для наборов сигналов с постоянной средней мощностью), как видно из рис. 9.21. В некодированной системе такое уменьшение расстояния снижает достоверность передачи. Однако вследствие избыточности, вносимой кодом, это уменьшение расстояния уже не сильно влияет на вероятность ошибки. Напротив, достоверность определяет просвет — минимальное расстояние между членами набора разрешенных кодовых последовательностей. Просвет описывает "наиболее простой способ совершения ошибки декодером (см. раздел 9.10.3.1). Независимо от используемого кода, пространство сигналов — это не самое удобное место для изучения улучшения достоверности, которое можно получить за счет кодирования. Это объясняется тем, что код определяется правилами и ограничениями, которые не видны в пространстве сигналов. Когда два сигнала находятся в непосредственной близости друг от друга в сигнальном пространстве кодовой системы, их близость может и не иметь существенного значения (с точки зрения вероятности ошибки), поскольку правила кода могут не допускать перехода между двумя такими якобы уязвимыми точками сигналов. Что же нужно для определения допустимых кодовых последовательностей и пространственных характеристик? Решетчатые диаграммы! При их использовании задача ТСМ — присвоение сигналов переходам в решетке, чтобы увеличить просвет между теми сигналами, которые вероятнее всего могут быть спутаны.
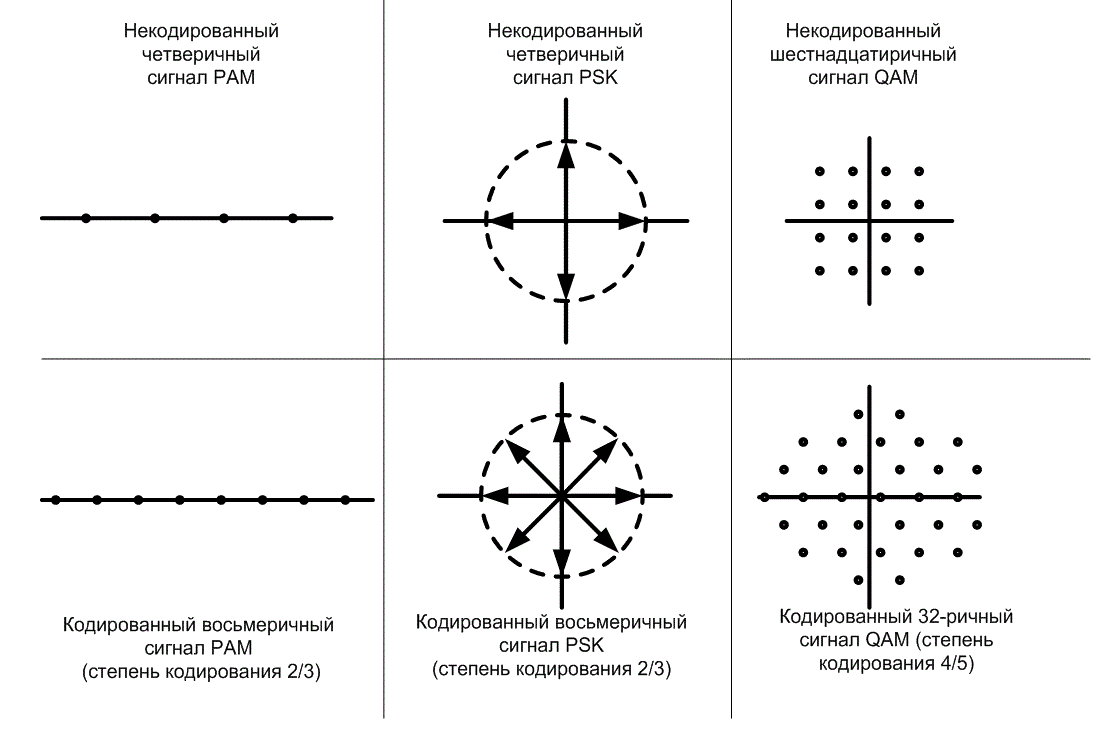
Рис. 9.21. Увеличение размера множества сигнала для решетчатого кодирования.
9.10.2. Кодирование ТСМ
9.10.2.1. Разбиение Унгербоека
Пусть приемник использует мягкую схему принятия решений, так что подходящей будет евклидова метрика расстояния. Для максимизации просвета (измеряемого по Евклиду) Унгербоек [31] предложил отображение кода в сигнал, следующее из последовательнЪго разбиения совокупности модулирующих сигналов на подмножества с возрастающими минимальными расстояниями d0< d1< d2... между элементами подмножеств. Эта идея продемонстрирована на рис. 9.22 для сигнального множества 8-PSK. На рис. 9.22 исходная совокупность сигнала обозначена через А0, а отдельные сигналы последовательно пронумерованы от 0 до 7. Если средняя мощность сигнала (квадрат амплитуды) выбрана равной единице, то расстояние d0 между любыми двумя соседними сигналами, очевидно, равно 2sin (
/8)=0,765. На первом уровне разбиения получаются подмножества В0и В1; где расстояние между соседними сигналами равно 
. На следующем уровне образуются подмножества с С0по С3, где расстояние между соседними сигналами равно уже d2=2. Структуру простых кодов (до восьми состояний) можно определить эвристически. В первую очередь выбирается подходящая решетчатая структура, что можно сделать, не задумываясь о конкретном кодере. ТСМ относится к классу методов кодирования формой сигнала, поскольку для описания этой концепции требуется только подходящая решетка и набор модулирующих сигналов; даже не нужно вводить понятие битов. Сигналы из расширенного множества М'=2k+1 сигналов присваиваются переходам в. решетке таким образом, чтобы максимизировать просвет (напомним, используется евклидово расстояние). При рассмотрении сверточных кодов в главе 7, переходы в решетке кодера (отражающие поведение цепи кодирования) помечались кодовыми битами. Для схемы ТСМ переходы в решетке помечаются модулирующими сигналами. Некодированный набор сигналов 4-PSK будет служить эталоном для кодированного набора 8-PSK. Этот эталонный набор, как показано на рис. 9.23, имеет тривиальную решетчатую диаграмму с одним состоянием и четырьмя параллельными переходами. Эта решетка тривиальна, поскольку решетка с одним состоянием означает, что в системе отсутствует память. Нет никаких ограничений или препятствий, чтобы в течение любого промежутка времени могли быть переданы сигналы 4-PSK; поэтому для такого некодированного случая оптимальный детектор просто независимо принимает ближайшие решения для каждого полученного зашумленного сигнала 4-PSK.
9.10.2.2. Отображение сигналов на переходы решетки
Унгербоек разработал эвристический набор правил [31] присвоения сигналам ветвей переходов решетки для получения эффективности кодирования, который позволяет сделать адекватный выбор состояний решетки. Правила построения решетки и разбиения множества сигнала (для модуляции 8-PSK) можно кратко изложить следующим образом.
1. Если за один интервал модуляции кодируется k бит, решетка должна разрешать для каждого состояния 2k возможных перехода в последующее состояние.
2. Между парой состояний может существовать более одного перехода.
3. Все сигналы должны появляться с равной частотой и обладать высокой регулярностью и симметрией.
4. Переходы с одинаковым исходным состоянием присваиваются сигналам либо из подмножества В0 , либо В1— их смешение недопустимо.
5. Переходы с одинаковым конечным состоянием присваиваются сигналам либо из подмножества В0 , либо В1 — их смешение недопустимо.
6. Параллельные переходы присваиваются сигналам либо из подмножества С0 , либо С1 либо С2, либо С3 — их смешение недопустимо.
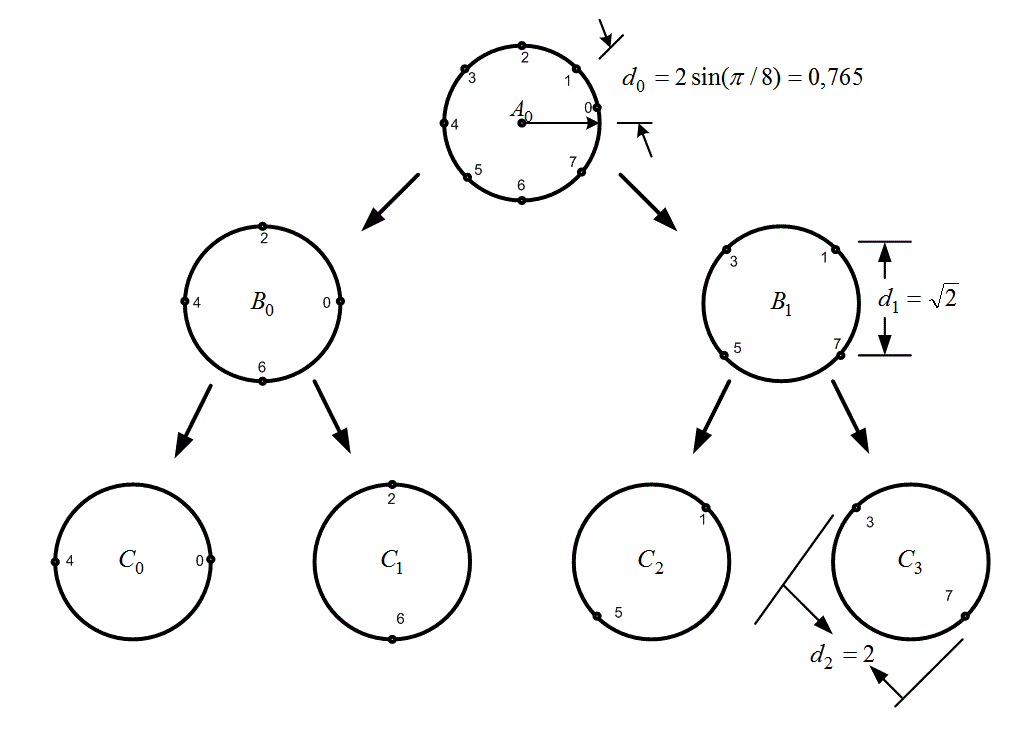
Рис.9.22. Разбиение Унгербоека набора сигналов 8-PSK
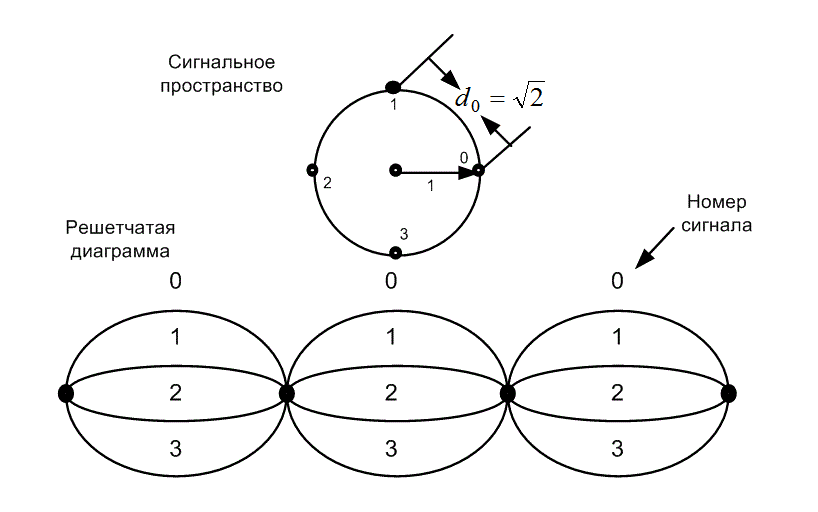
Рис. 9.23. Некодированное множество сигналов 4-PSK и его решетчатая диаграмма с одним состоянием.
Правила гарантируют, что код, построенный таким образом, будет иметь регулярную структуру и просвет, всегда превышающий минимальное расстояние между точками сигнала исходной некодированной модуляции. На рис. 9.24 показано возможное отображение кода в сигнал с использованием решетки с четырьмя состояниями с параллельными путями. Присвоение сигналу кода производится посредством изучения разбитого пространства сигналов (рис. 9.22), решетчатой диаграммы, показанной на рис. 9.24, и правил, перечисленных выше. На переходах решетки написаны номера сигналов, присвоенных этим переходам согласно правилам разбиения. Отметим, что для модуляции 8-PSK присвоение сигнала осуществлялось согласно правилу 1: имеется k+1=3 кодовых бита, следовательно k=2 информационных бита, а на входе и выходе каждого состояния имеется 22 = 4 перехода. Присвоение сигналов осуществлялось согласно правилу 6, поскольку каждой паре параллельных переходов был присвоен сигнал одного из наборов С0, С1, С2 или С3. Кроме того, присвоение согласуется с правилами 4 и 5, поскольку четырем ветвям, выходящим в состояние (или покидающим состояние), были присвоены сигналы из набора В0или B1. На рис. 9.24 состояния решетки различаются согласно типам сигналов, которые могут появиться на переходах, покидающих это состояние. Таким образом, состояния можно обозначить с помощью подмножеств сигнала как состояние C0C1 или С2С3 либо (другой возможный способ обозначения с помощью номеров сигнала) как состояние 0426, 1537 и т.д. На рис. 9.24 показаны обе системы обозначений. Из этого присвоения модулирующих сигналов переходам в решетке согласно правилам разбиения следует спецификация решетчатого кодера. Отметим, что окончательное присвоение битов кода сигналу (отображение кодового слова в переход) можно теперь выполнить произвольно. Хотя может показаться несколько странным, что теперь можно безнаказанно присваивать биты переходам в решетке и сигналам, стоит напомнить, что схемы кодера еще не существует. Следовательно, еще нет битов и переходы в решетке могут иметь только тот смысл, который для них выберем мы. Каковы же последствия такого произвольного присвоения? Выбор различных отображений кодовых слов в переходы отразится на структуре кодера. Следовательно, если повезет, будет реализована схема кодера, выходные биты которого будут соответствовать способу, которым осуществлялось их присваивание переходам между состояниями. В противном случае такое конструктивное решение реализовать будет сложно. При некотором выборе способа присвоения кодовых слов конструкция кодера будет проще, в то время как другой выбор может обусловить громоздкость его конструкции.
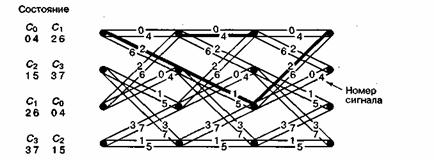
Рис. 9.24. Решетка с четырьмя состояниями с параллельными путями.
Решетка, аналогичная показанной на рис. 9.24, вскоре будет исследована в контексте обнаружения и декодирования, чтобы проверить, обеспечивается ли эффективность кодирования при учете в процессе кодирования правил Унгербоека.
9.10.3. Декодирование ТСМ
9.10.3.1. Ошибочное событие и просвет
Задача сверточного декодера заключается в определении пути, пройденного сообщением в кодирующей решетке. Если все входящие последовательности сообщений равновероятны, декодером с минимальной вероятностью появления ошибки будет декодер, сравнивающий условные вероятности P(Z|U(m)) (где Z — полученная последовательность сигналов, a U(m) — одна из возможных переданных последовательностей сигналов) и выбирающий максимальную. Этот критерий принятия решений, известный как критерий максимального правдоподобия, описан в разделе 7.3.1. Нахождение последовательности U(m), которая максимизирует P(Z|U(m)), эквивалентно нахождению последовательности U(m), которая наиболее похожа на Z. Поскольку декодер, работающий по принципу максимального правдоподобия, выберет такой путь по решетке, которому будет соответствовать последовательность U(m’), находящаяся на минимальном расстоянии от полученной последовательности Z, задача определения максимального правдоподобия будет идентична задаче нахождения самого короткого расстояния по решетчатой диаграмме.
Поскольку сверточный код — это групповой (или линейный) код, набор расстояний, которые нужно проверить, не зависит от того, какая последовательность выбрана в качестве проверочной. Вследствие этого, не теряя общности, в качестве проверочной можно выбрать последовательность, целиком состоящую из нулей, показанную на рис. 9.25 пунктирной линией. В предположении, что была передана нулевая последовательность, ошибочное событие определяется как отклонение от нулевого пути с последующим возвратом на этот путь. Ошибочные события начинаются и заканчиваются состоянием a и не возвращаются в это состояние нигде в промежуточной области. На рис. 9.25 показано ошибочное сообщение в решетчатом коде, т.е. на рисунке изображена переданная нулевая последовательность, помеченная как U=...,U1 ,U2, U3,..., и альтернативная последовательность, помеченная как V=..., V1, V2, V3,... . Видно, что альтернативная последовательность сначала отклоняется, а затем снова сливается с переданной последовательностью. Если предположить, что осуществляется мягкое декодирование, сообщение принимается ошибочно тогда, когда полученные символы ближе (евклидово расстояние) к некоторой возможной последовательности V, чем к реальной переданной последовательности U. Из этого следует, что коды для сигналов многоуровневой/фазовой модуляции должны строиться таким образом, чтобы достигать максимального евклидова просвета; чем больше просвет, тем меньше вероятность ошибки. Следовательно, присвоение сигналов переходам решетки в кодере таким образом, чтобы максимизировать евклидов просвет (см. раздел 9.10.2), — это ключ к оптимизации решетчатых кодов.
9.10.3.2. Эффективность кодирования
Рассмотрим мягкую схему принятия решений, декодирование по принципу максимального правдоподобия, единичную среднюю мощность сигнала и гауссово распределение шума с дисперсией 
2 на размерность. В этом случае нижний предел вероятности ошибочного события можно выразить через просвет df [32].
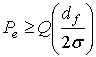(9.55)
где Q(•) — гауссов интеграл ошибок, определенный в формуле (3.43). Использование термина "ошибочное событие" (error event) вместо "битовая ошибка" (bit-error) объясняется тем, что ошибка может распространяться на более чем один бит. При большом значении отношения сигнал/шум (signal-to-noise ratio — SNR) предел в уравнении (9.55) асимптотически точен. Асимптотическая эффективность кодирования G в децибелах относительно некоторой некодированной эталонной системы с аналогичными средней мощностью сигнала и дисперсией шума выражается как отношение расстояний или квадратов расстояний и записывается в следующем виде.
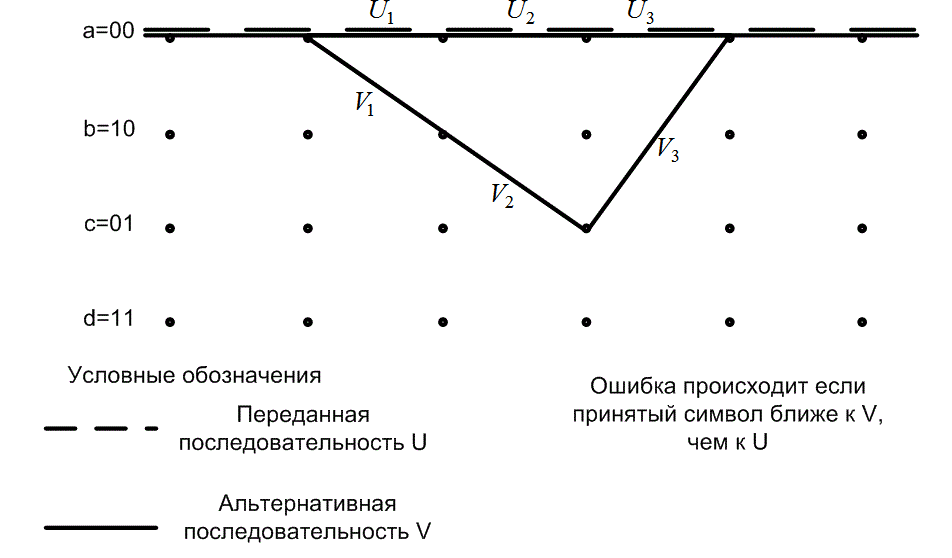
Рис. 9.25. Пример ошибочного события
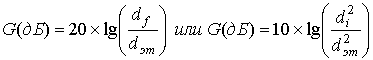(9.56)
где df и (dэт — евклидов просвет кодированной системы и некодированной эталонной системы. Отметим, что для больших значений SNR и данной вероятности появления ошибки формула (9.56) дает те же результаты, что и выражение для эффективности кодирования (6.19), повторно приведенное ниже.
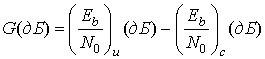(9.57)
Здесь (Eb/N0)u и (Eb/N0)с являются требуемыми (Eb/N0) (в децибелах) для некодированной и кодированной систем. Следует помнить, что эффективность кодирования, выраженная в виде (9.56), дает ту же информацию (при больших значениях SNR), что и более привычное выражение для повышения достоверности передачи (9.57). По сути, формула (9.56) резюмирует основную задачу кода ТСМ. Эта задача — добиться просвета, превышающего минимальное расстояние между некодированными модулирующими сигналами (при той же скорости передачи информации, ширине полосы частот и мощности).
9.10.3.3. Эффективность кодирования для схемы 8-PSK при использовании решетки с четырьмя состояниями
Вычислим теперь эффективность кодирования для решетки с четырьмя состояниями в схеме 8-PSK, разработанной согласно правилам кодирования из раздела 9.10.2.2. Решетка на рис. 9.24 теперь будет исследоваться в контексте процедуры декодирования. Сначала в качестве настроечной выбирается нулевая последовательность. Иными словами, предполагается, что передатчик отправил последовательность, содержащую только копии сигнала номер 0. Чтобы продемонстрировать преимущества такой системы ТСМ (используя алгоритм декодирования Витерби), нужно показать, что самый простой способ совершения ошибки в кодированной системе сложнее самого простого способа совершения ошибки в некодированной системе. Необходимо изучить всевозможные отклонения от верного пути с последующим слиянием с верным путем (нулевой последовательностью) и найти тот, который имеет минимальное евклидово расстояние до правильного пути. Рассмотрим сначала возможный путь ошибочного события (рис. 9.24), который затемнен и помечен номерами сигнала 2, 1, 2. Квадрат расстояния до нулевого пути вычисляется как сумма квадратов отдельных расстояний между сигналами 2 и 0; 1 и 0; и 2 и 0. Отдельные расстояния берутся из диаграммы разбиения на рис. 9.22, в результате чего получаем следующее.
или
(9.58)
В уравнении (9.58) евклидово расстояние d получается точно так же, как и результирующий вектор в евклидовом пространстве, т.е. как квадратный корень из суммы квадратов отдельных компонентов (расстояний). На рис. 9.24 есть путь с отклонением и повторным слиянием, который имеет евклидово расстояние, меньшее d = 2,2. Это затененное ошибочное событие (помеченное как сигнал 4) происходит, если (при использовании декодирования Витерби) вместо правильного пути, связанного с сигналом 0, выживает параллельный. Может возникнуть вопрос: если декодер выбирает параллельный путь (т.е. последующее состояние одинаково в обоих случаях), будет ли это в действительности серьезной ошибкой. Если параллельный путь — это неправильно выбранный путь (это все-таки путь с отклонением и повторным слиянием, даже если он занимает только один промежуток времени), то позже, когда будут введены схемы кодеров и биты, выживший сигнал 4 даст в результате неверное значение бита. Расстояние от пути сигнала 4 до пути сигнала 0 равно, как видно из рис. 9.22, d=2. Это расстояние меньше, чем расстояние для любого другого ошибочного события (можете проверить!); поэтому евклидов просвет для этой кодированной системы равен df=2. Минимальное евклидово расстояние для набора некодированных эталонных сигналов на рис. 9.23 равно 
. Теперь для вычисления асимптотической эффективности кодирования следует воспользоваться уравнением (9.56), что даст следующее.
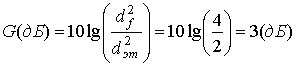(9.59)
9.10.4. Другие решетчатые коды
9.10.4.1. Параллельные пути
Если число состояний меньше размера набора кодированных сигналов M' решетчатая диаграмма требует параллельных путей. Следовательно, решетка с четырьмя состояниями для модуляции 8-PSK требует наличия параллельных путей. Чтобы лучше понять причины этого, обратимся еще раз к первому правилу Унгербоека: если за один интервал модуляции кодируется k бит, решетка должна разрешать для каждого состояния 2k возможных перехода в последующее состояние. Для рассматриваемого случая 8-PSK каждый сигнал представляет k+1=3 кодовых бит или k=2 бит данных. Поэтому из первого правила следует наличие 2k = 22 = 4 переходов в каждое последующее состояние. На первый взгляд решетка с четырьмя состояниями без параллельных путей может удовлетворить такому условию, если реализовать полностью замкнутую решетку (каждое состояние связано со всеми последующими состояниями). Однако попробуйте нарисовать полностью замкнутую решетку с четырьмя состояниями без параллельных путей, удовлетворяя при этом правилам 4 и 5 для системы 8-PSK. Это невозможно! Нарушение правил приведет к результатам, близким к оптимальным. В следующем разделе показана решетка с восемью состояниями для схемы 8-PSK (количество состояний уже не меньше M'), где могут быть соблюдены все правила разбиения без требования наличия параллельных путей.
9.10.4.2. Решетка с восемью состояниями
После экспериментирования с использованием различных структур решетки и присвоением канальных сигналов, в качестве оптимального для восьми состояний был выбран код 8-PSK, показанный на рис. 9.26 [31]. Путь ошибочного события с минимальным расстоянием до нулевого пути помечен номерами сигналов 6, 7, 6. Поскольку здесь отсутствуют параллельные пути, ограничивающие евклидов просвет, квадрат этого просвета равен 
, где расстояния d0 и d1, получены из рис. 9.22. Асимптотическая эффективность кодирования системы ТСМ с восемью состояниями относительно эталонной системы 4-PSK равна следующему.
(9.60)
Подобным образом можно показать, что решетчатая структура с шестнадцатью состояниями для кодированной совокупности 8-PSK дает эффективность кодирования 4,1 дБ, по сравнению с некодированной схемой 4-PSK [31]. Если состояний меньше восьми, дополнительная эффективность кодирования может быть получена путем введения асимметрии в совокупность модулирующих сигналов [33].
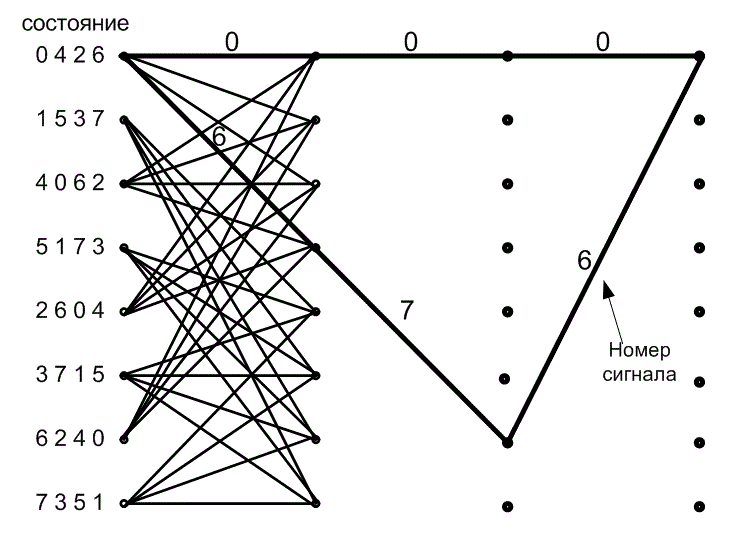
Рис. 9.26. Решетчатая диаграмма с восьмью состояниями для кода 8-PSK
9.10.4.3. Решетчатое кодирование для схемы QAM
Метод разбиения набора сигналов можно применять и к другим типам модуляции. Рассмотрим использование кодированной схемы 16-QAM с тремя информационными битами на интервал модуляции, где в качестве эталонной системы выбрана некодированная 8-PSK. Для нормированное пространства 16-QAM выберем среднее значение квадрата амплитуды набора сигналов, равное единице, что дает rf0 = 2/VlO. На рис. 9.27 показано разбиение сигналов 16-QAM на подмножества с возрастающими расстояниями между элементами (d0 < d{ < d-i <'d3). Кодовая система 16-QAM с восемью состояниями, полученная путем разбиения набора согласно описанной ранее процедуре, показана на рис. 9.28 [31]. Путь ошибочной комбинации с минимальным расстоянием обозначен как D6, D5, D2. Хотя при использовании схемы ТСМ имеется эффективность кодирования, при декодировании расширенного пространства сигнала существует потенциальная неопределенность фазы, которая может серьезно ухудшить достоверность передачи. Вей (Wei) [34] применил концепцию дифференциального кодирования к методам ТСМ; полученные при этом коды не зависят от поворотов элементарных сигналов на углы 90°, 180° и 270°.
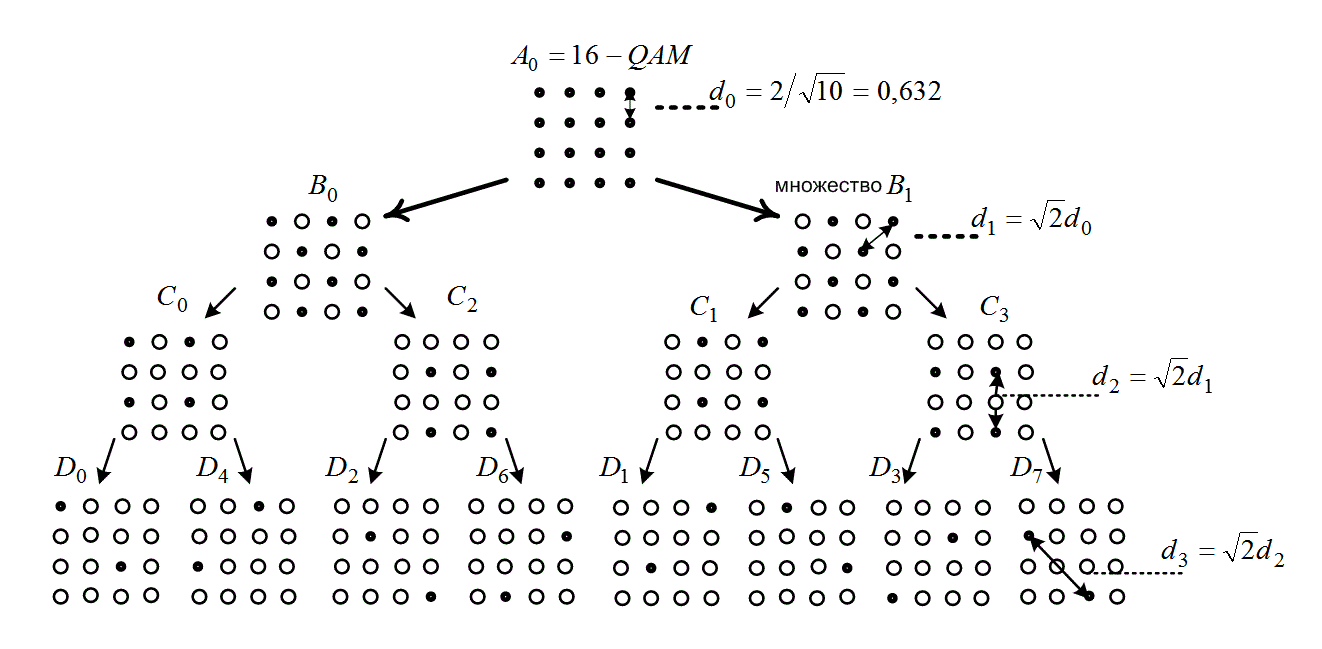
Рис. 9.27. Разбиение Унгербоека сигналов 16-QAM
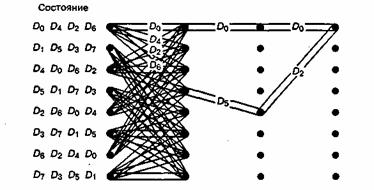
Рис. 9.28. Решетчатая диаграмма с восемью состояниями для передачи сигнала 16-QAM
Вкратце можно сказать, что решетчатое кодирование в узкополосных каналах включает больший алфавит сигналов (т.е. M-арные схемы РАМ, PSK или QAM) для компенсации избыточности, которая вводится при кодировании; таким образом, ширина полосы частот канала не возрастает. Даже если увеличение размера набора сигналов уменьшает минимальное расстояние между сигналами, евклидов просвет между разрешенными кодовыми последовательностями превышает величину, необходимую для компенсации этого уменьшения. В результате полная эффективность кодирования равна от 3 до 6 дБ без какого-либо расширения полосы частот [6, 31]. В следующем разделе эти идеи будут дополнительно проиллюстрированы на примере.
9.10.5. Пример решетчатого кодирования
В предыдущем разделе обсуждалось отображение сигналов в переходы решетки безотносительно к конечному отображению канальных символов (кодовых битов или кодовых слов) в переходы решетки. В этом разделе пример решетчатого кодирования начнется с рассмотрения точного определения структуры кодера. Структура кодера автоматически определяет решетчатую диаграмму и присвоение кодовых слов переходам решетки. Следовательно, в этом примере, если сигналы присвоены переходам решетки (а значит, подразумевающимся кодовым словам), уже нет возможности произвольно присваивать кодовые слова сигналам, как это делалось ранее при отсутствии схемы кодера.
Рассмотрим кодер, использующий сверточный код со степенью кодирования 2/3 для передачи двух бит информации за один интервал модуляции. Пример подобного кодера показан на рис. 9.29. Степень кодирования 2/3 достигается путем передачи без изменения одного бита из каждой пары битов исходной последовательности и кодирования второго бита двумя кодовыми битами (выполняется кодером со степенью кодирования 1/2 и длиной кодового ограничения К=3). Как показано на рисунке, биты из входящей последовательности попадают в сдвиговый регистр только через один (m2,m4,...). Может возникнуть вопрос: насколько может быть хорошей такая система, если преимущества, определяемые избыточностью, получают только 50% бит. Напомним пример с волшебником, который определял, что некоторые биты довольно уязвимы и поэтому они присваивались модулирующим сигналам с наилучшими пространственными характеристиками, в то время как другие считались устойчивыми и присваивались сигналам с худшими пространственными характеристиками. Модуляция и кодирование происходят одновременно; якобы "некодированные" не будут забыты, они выиграют от присвоения наилучших сигналов. Следует подчеркнуть, что кодирование и декодирование в схеме ТСМ происходит преимущественно на сигнальном уровне (в нашем первом описании ТСМ о каком-либо кодере не упоминалось), тогда как в традиционном коде с исправлением ошибок кодирование и декодирование происходит только на битовом уровне.
Решетчатая диаграмма на рис. 9.30 описывает схему кодера с рис. 9.29. Как и в главе 7, названия состояний соответствуют содержимому крайних правых К-1=2 разрядов регистра сдвига. Параллельные переходы на решетке (рис. 9.30) обусловлены некодированными битами; некодированный бит представляется крайним левым битом каждого перехода решетки. В каждом состоянии начинается четыре перехода. Для каждого состояния имеется два верхних перехода — от пары входных информационных битов (m1m2 равны 00 и 10); два нижних перехода проистекают от пары 01 и 11. На рис. 9.30 показана решетчатая структура, подобная показанной на рис. 9.24, за исключением того, что каждый переход на рис. 9.30 обозначен назначенным ему кодовым словом. Стоит повторить, что схема кодера определяет, какие кодовые слова появляются на переходах решетки; разработчик системы только присваивает сигналы переходам. Следовательно, когда уже имеется схема (поведение которой описывается решеткой), любой сигнал, присвоенный переходу в решетке, автоматически становится носителем кодового слова, которое соответствует этому переходу.
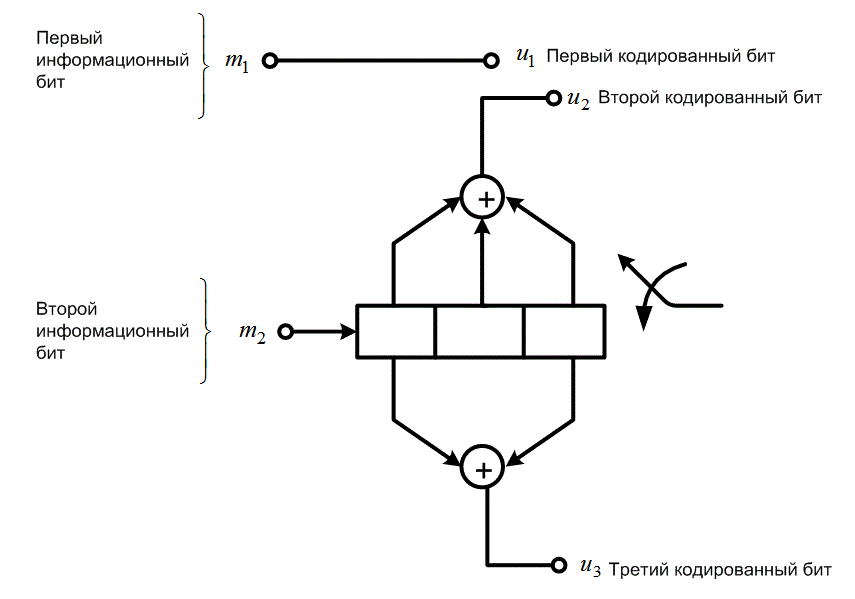
Рис. 9.29. Сверточный кодер со степенью кодирования 2/3.
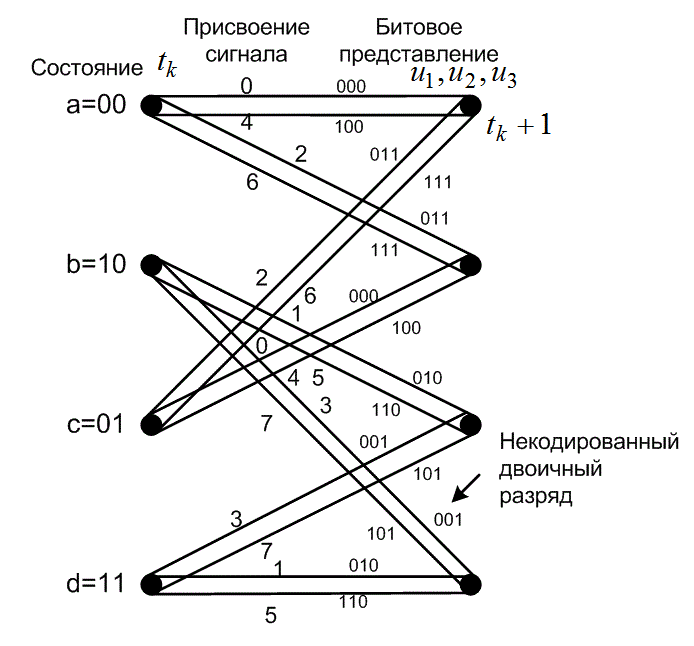
Рис. 9.30. решетчатая диаграмма для кода со степенью кодирования 2/3.
Пусть кодовая модуляция — это 8-ричная амплитудно-импульсная модуляция (8-ary pulse amplitude modulation — 8-РАМ), как показано на рис. 9.31. На рис. 9.31, а показан кодированный набор сигналов, где для каждого сигнала евклидово расстояние до центра пространства сигналов показано в некоторых произвольных единицах, причем сигналы расположены на равных расстояниях один от другого и симметрично относительно нуля. На рис. 9.31, б показан эталонный набор 4-ричной схемы РАМ, в котором точки сигнала и расстояния помечены аналогичным образом. Важным этапом в разработке кодера является присвоение 8-ричных сигналов РАМ переходам решетки согласно правилам разбиения Унгербоека (рис. 9.32). Изучение этих правил может привести к такому же присвоению номеров сигналов переходам решетки, как показано на рис. 9.24. Подобное присвоение сигналов, а также кодовые слова, присвоенные схемой кодера, показаны на рис. 9.30. Наиболее несопоставимая пара сигналов (с расстоянием d2=8) была присвоена наиболее уязвимым (в плане появления ошибок) параллельным переходам. Кроме того, как следует из правил Унгербоека, сигналы со следующим наибольшим расстоянием (d1=4) были присвоены переходам, выходящим или входящим в одно и то же состояние. Для удобства на рис. 9.31, а показано также присвоение кодовых слов сигналам (результат отображения сигналов в переходы решетки).
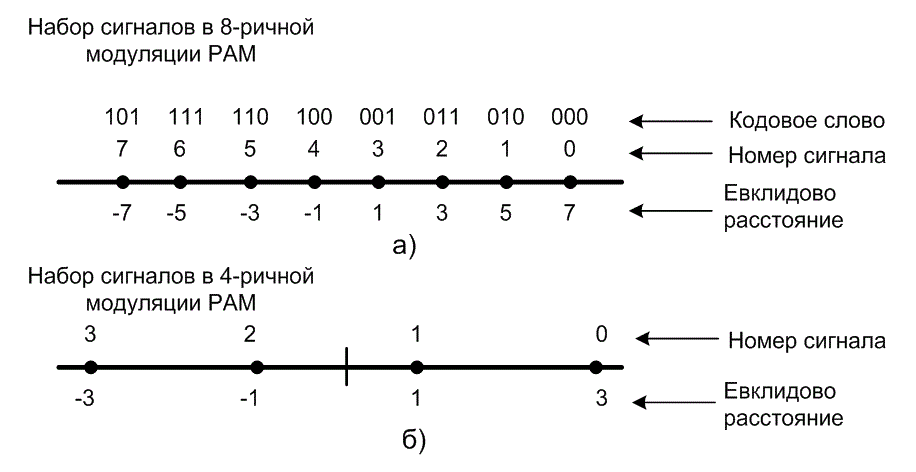
Рис. 9.31. Множество сигналов: а) кодированная 8-ричная PAM, б) некодированная 4-ричная PAM.
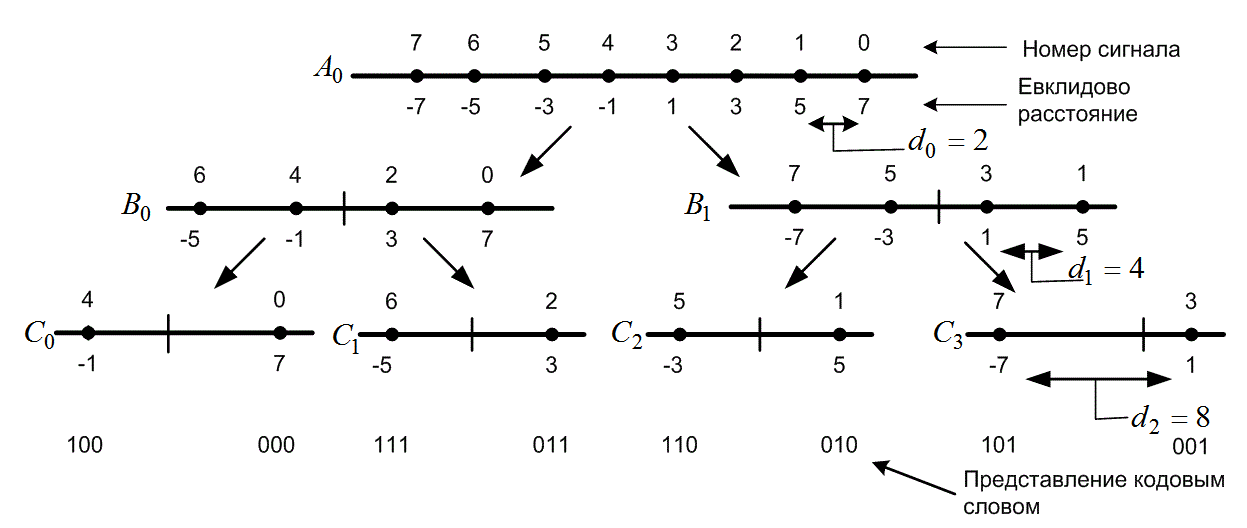
Рис. 9.32. Разбиение Унгербоека сигналов 8-PAM
На рис. 9.24 путь ошибочного события, помеченный номерами сигналов 2, 1,2, — это путь с минимальным расстоянием для нашего примера модуляции 8-РАМ. Расстояние до нулевого пути вычисляется с использованием формулы (9.58). В этом примере, если взять отдельные расстояния с рис. 9.32, df вычисляется следующим образом.
или (9.61)
Можно легко убедиться, что для такого типа модуляции параллельный путь (с d=8) не будет ошибочным путем с минимальным расстоянием (как это было для 8-PSK). Далее для нахождения эталонного расстояния для 4-РАМ из рис. 9.31, б находим, что 
=2. Теперь для этого примера можем вычислить асимптотическую эффективность кодирования, сравнивая квадрат евклидова просвета кодированной системы с евклидовым просветом эталонной системы. Однако тут необходимо убедиться в том, что средняя мощность сигналов в каждом наборе одинакова. В предыдущем примере схемы 8-PSK выбор единичной окружности для кодированной и некодированной систем означал, что средняя мощность сигнала была одинакова в обоих наборах. Однако в этом примере ситуация несколько иная. Следовательно, для вычисления асимптотической эффективности кодирования требуется нормировать следствие неравенства средней мощности набора сигналов, т.е. видоизменить выражение (9.56) [35]. Соответственно записываем
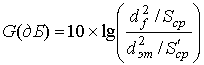(9.62)
где Sср, и 
— средняя мощность сигналов в кодированном и эталонном наборах. Расстояние соответствует амплитуде сигнала или напряжению; таким образом, квадрат расстояния соответствует квадрату напряжения, или мощности. Следовательно, средняя мощность сигнала из совокупности вычисляется как
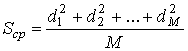(9.63)
где di — евклидово расстояние от центра пространства доi-гo сигнала, а М — количество кодовых символов в этом множестве. Для набора сигналов 8-РАМ, показанного на рис. 9.31, а, уравнение (9.63) дает значение 
=21. Для эталонного набора сигналов 4-РАМ, показанного на рис. 9.31, б, уравнение (9.63) дает значение S'cp = 5.
При использовании уравнения (9.62) асимптотическая эффективность кодирования для системы 8-РАМ будет иметь следующий вид.
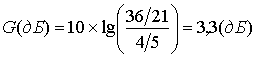(9.64)
Увеличивая количество состояний решетки (большая длина кодового ограничения) за счет возрастающей сложности декодирования, можно добиться большей эффективности кодирования. При кодировании сигналов 8-РАМ со степенью кодирования 2/3 решетка с 256 состояниями даст эффективность кодирования, на 5,83 дБ большую относительно набора сигналов 4-РАМ [9]. В этом случае вследствие использования решетчатого кодирования будет иметь место только незначительное увеличение сложности передатчика. Задача декодирования в приемнике становится более сложной, однако использование больших интегральных схем (large scale integrated — LSI, БИС) и сверхскоростных интегральных схем (high-speed integrated circuit — VHSIC, ССИС). делает такой метод кодирования чрезвычайно привлекательным для достижения значительной эффективности кодирования без расширения полосы пропускания.
9.10.6. Многомерное решетчатое кодирование
В разделе 9.9.3 подчеркивалось, что при данной скорости передачи данных передача сигналов в двухмерном пространстве может давать ту же достоверность, что и передача в одномерном пространстве РАМ, но при меньшей средней мощности. Это достигается путем выбора точек сигналов на двухмерной решетке из области с кольцевой, а не прямоугольной границей. Выполняя подобное при более высоких размерностях, можем видеть, что потенциальная экономия энергии приближается к 1,53 дБ при N, стремящемся к бесконечности. В реальных системах при такой многомерной передаче сигналов можно достичь экономии энергии (эффективность выбора формы) порядка 1 дБ относительно одномерной передачи [21, 36, 37]. В стандарте высокоскоростных модемов V.34 определена 16-мерная модуляция QAM; используемый метод отображения битов в точки пространства высшей размерности называется отображением оболочки (shell mapping); соответствующая эффективность выбора формы равна 0,8 дБ [16]. Используя четырех-, восьми- и шестнадцатимерную совокупности сигналов, можно получить некоторые преимущества по сравнению с обычными двухмерными схемами — меньшие двухмерные блоки совокупности, повышение устойчивости к неопределенности фазы, более выгодные компромиссы между эффективностью кодирования и сложностью реализации. Множество подобных систем представлено и охарактеризовано в работе [36]. (Читателям, заинтересованным в дальнейшем изучении кодовой модуляции, в частности решетчатого кодирования, рекомендуется обратиться к работам [38—46].)