5.5.4. Суммарный шум-фактор и общая шумовая температура
5.5.5. Эффективная температура системы
5.5.6. Шумовая температура неба
5.5.1. Коэффициент шума
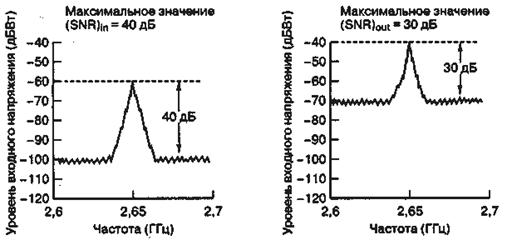
Коэффициент шума F (или шум-фактор) (noise figure) связывает значение параметра SNR на входе сети со значением на выходе. Таким образом шум-фактор измеряет ухудшение SNR, вызванное прохождением через сеть. Пример сказанного приведен на рис. 5.14. На рис. 5.14, а показано значение параметра SNR на входе усилителя (обозначено как (SNR);,,) в зависимости от частоты. Максимальное значение на 40 дБ превышает минимальный уровень шума. На рис. 5.14, б значение параметра SNR показано на выходе усилителя (обозначено как (SNR)out). За счет усиления на усилителе мощность сигнала возросла на 20 дБ, но при этом усилитель добавил к сигналу собственный шум. Максимальное значение сигнала на выходе всего на 30 дБ превышает минимальный уровень шума. Получаем, что ухудшение SNR на пути от входа до выхода составляет 10 дБ; это равносильно утверждению, что коэффициент шума усилителя равен 10 дБ. Коэффициент шума — это параметр, выражающий шумовые свойства двухпортовой сети или некоторого устройства, такого как усилитель, относительно эталонного источника шума в входном порту. Записать шум-фактор можно следующим образом.
(5.25)
где
Sj — мощность сигнала во входном порту усилителя
Ni — мощность шума во входном порту усилителя
Nai — шум усилителя относительно входного порта
С — коэффициент усиления усилителя
а) б)
Рис. 5.14. Уровни шума и сигнала усилителя как функция частоты: а) вход усилителя; б) выход усилителя
Иллюстрация уравнения (5.25) приведена на рис. 5.15. На рис. 5.15, а представлен реализуемый усилитель с коэффициентом усиления G = 100 и мощностью внутреннего шума Na = 10 мкВт. Мощность источника шума, внешнего по отношению к усилителю, равна N, = 1 мкВт. На рис. 5.15, б усилитель предполагается идеальным, и мы приписали шумовые свойства реального усилителя, изображенного на рис. 5.15, а, внешнему источнику Nai, последовательно соединенному с исходным источником Ni. Значение Nai получается путем уменьшения Na на величину, равную коэффициенту усиления усилителя. Как показано на рис. 5.15, б, уравнение (5.25) соотносит все шумы с входом усилителя, независимо от того, где в действительности присутствует шум — на входе устройства или вне его. Как видно из рис. 5.15, мощность шума на выходе реального усилителя идентична тому, что дает эквивалентная модель.
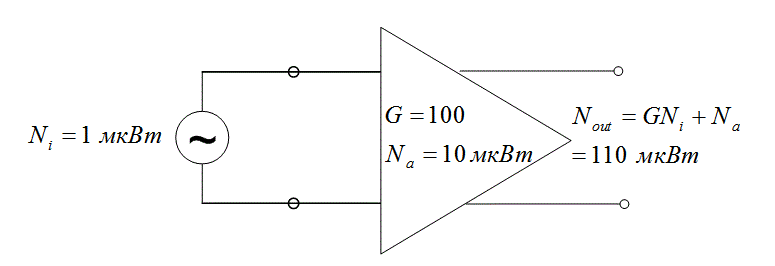
а)
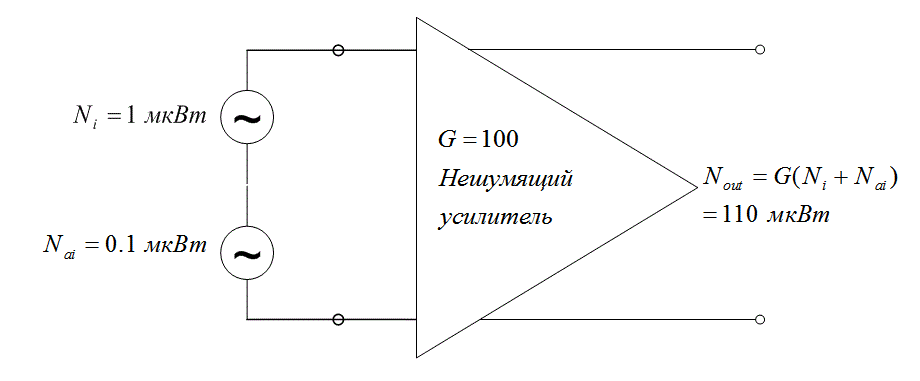
б)
Рис. 5.15. Пример трактовки шума в усилителях
После упрощения уравнения (5.25) получаем следующее.
(5.26)
Из полученного уравнения видим, что коэффициент шума выражает шумовые свойства сети относительно входного источника шума; коэффициент шума — это не абсолютная мера шума. Идеальный усилитель или идеальная сеть, не вносящие шума (Nai = 0), имеют шум-фактор, равный единице (0 дБ).
Для практического использования понятия шум-фактор мы должны научиться делать объективные сравнения устройства на основе уравнения (5.26). Следовательно, в качестве эталонного мы должны выбрать значение Ni. Шум-фактор любого устройства будет представлять меру того, насколько более шумным (по сравнению с эталонным) является рассматриваемое устройство. В 1944 году Фриис (Friis) [9] предложил, чтобы шум-фактор определялся для источника шума при эталонной температуре Т0°= 290 К. Впоследствии это предложение было принято ШЕЕ как часть стандартного определения шум-фактора [10]. Из уравнения (5.17) видим, что для задания максимальной доступной спектральной плотности мощности шума из любого источника достаточно задать температуру этого источника. Значение 290 К было выбрано в качестве эталонного, поскольку именно оно является разумной приближенной оценкой температуры источника большинства каналов связи. Кроме того, если выбрать Т0° = 290 К, то вычисление спектральной плотности шума N0 при этой температуре дает эстетически красивое значение.
или (в децибелах)
Теперь, когда мы определили шум-фактор F относительно источника шума с температурой 290 К, важно отметить, что соотношения (5.25) и (5.26) справедливы строго, только если N, — это источник шума с температурой 290 К. При других Ni нужно переименовать коэффициент F в уравнениях (5.25) и (5.26) и использовать термин эксплуатационный коэффициент шума Fор. Связь Fор и F показана ниже, в уравнении (5.48).
5.5.2. Шумовая температура
Преобразовав уравнение (5.26), можем записать следующее.
(5.27)
Из уравнения (5.16) можем подставить 
, где Т0° — эталонная температура источника, a TR° — эффективная шумовая температура приемника (или сети). Затем можем записать следующее.
или
Температура Т0° выбрана равной 290 К, поэтому получаем следующее.
(5.28)
В уравнении ,(5.26) понятие коэффициента шума использовано для описания шумовых характеристик усилителя. Уравнение (5.28) — это альтернативная (и при этом эквивалентная) характеристика, именуемая эффективной шумовой температурой. Напомним, что шум-фактор — это измерение относительно эталона. Шумовая температура такого ограничения не имеет.
Характеристики источников шума (в контексте уравнения (5.17)) можно описывать как через доступную спектральную мощность шума, так и эффективную шумовую температуру. Уравнение (5.28) показывает, что шумовые свойства усилителя можно смоделировать с помощью введения дополнительного источника шума, подобного изображенному на рис. 5.15, б, работающего при некоторой эффективной температуре, обозначенной ТR°. Для чисто резистивного оконечного устройства ТR° всегда превышает температуру окружающей среды (разумеется, если устройство не охлаждается специально). Важно заметить, что в реактивных оконечных устройствах, таких как неохлаждаемые параметрические усилители или другие малошумящие устройства, TR° может быть значительно меньше 290 К, даже если температура окружающей среды выше этой величины [11]. Чтобы записать выход усилителя как функцию его эффективной температуры, мы можем использовать уравнения (5.16), (5.25) и (5.28):
(5.29,a)
(5.29,6)
(5.29,в)
где Т° — температура источника, а Т0° равна 290 К.
5.5.3. Потери в линии связи
Отличия между сетями усилителей и сетями с потерями в линии можно рассматривать в контексте механизмов потерь и шумов, описанных ранее. Сети с шумами рассматривались в разделах 5.5.1 и 5.5.2 и подразумевали использование усилителей. Говорилось, что ухудшение параметра SNR происходит вследствие введения в линию связи дополнительного шума (усилителя), как показано на рис. 5.15. В то же время в случае линии с потерями мы должны показать, что ухудшение параметра SNR происходит вследствие поглощения сигнала при фиксированном уровне шума (когда температура линии меньше (или равна) температуры источника). Впрочем, и в этом случае ухудшение будет выражено через увеличение коэффициента шума или эффективной шумовой температуры.
Рис. 5.16. Линия с потерями: импеданс и температура согласованы на обоих концах
Рассмотрим линию (или сеть) с потерями, показанную на рис. 5.16. Предположим, что линия согласована с источником и нагрузкой по импедансу. Определим потерю мощности следующим образом.
Коэффициент усиления сети G равен 1/L (меньше единицы для линии с потерями). Пусть все компоненты работают с температурой Тg°. Общий шум, поступающий с выхода сети в нагрузку, равен
,
поскольку при температуре Tg° выход сети выглядит как чистое сопротивление. Для обеспечения теплового равновесия общая мощность, поступающая с нагрузки обратно в сеть, также должна равняться УУ0. Напомним, что доступная мощность шума KToW зависит исключительно от температуры, ширины полосы и согласования импедансов; она не зависит от значения сопротивления. 
можно разбить на два компонента, Ngo и GNLi.
(5.30)
(5.31)
является компонентом выходной мощности шума, связанным с источником, GKLi — компонентом выходной мощности шума, отвечающим за сеть с потерями, a NLi — шумом сети, измеряемым относительно ее входа. Объединяя уравнения (5.30) и (5.31), можем записать следующее.
(5.32)
Выразим 
(5.33)
Следовательно, эффективная шумовая температура линии равна следующему.
(5.34)
Поскольку G = 1/L, то
(5.35)
В качестве эталонной температуры выберем 
= 290 К. Тогда можем записать следующее.
(5.36)
С помощью уравнений (5.28) и (5.36) можем выразить шум-фактор для линии с потерями.
(5.37)
Если сеть является линией с потерями, такой что F = L и G=1/L, то Nout в уравнении (5.29,в) приобретает следующий вид.
(5.38)
Отметим, что некоторые авторы используют параметр L для обозначения величины, обратной к введенному нами коэффициенту потерь. В таких случаях шум-фактор F= 1/L.
Пример 5.4. Линия с потерями
Линия с температурой 
= 290 К проложена от источника с шумовой температурой 
= 1450 К. Мощность входящего сигнала Si равна 100 пиковатт (пВт), а ширина полосы сигнала W — 1 ГГц. Коэффициент потерь линии L = 2. Определите (SNR)in, эффективную температуру линии 
, мощность выходного сигнала Sout и (SNR)out.
Решение
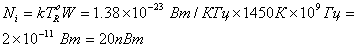
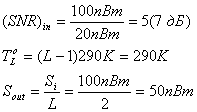
Используя уравнение (5.29), получаем следующее.
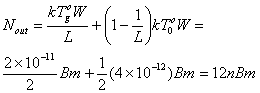
и
5.5.4. Суммарный шум-фактор и общая шумовая температура
Если две сети соединены последовательно, как показано на рис. 5.17, а, суммарный шум-фактор можно записать следующим образом.
Здесь 
— коэффициент усиления, связанный с сетью 1. Если последовательно соединены n сетей, выражение (5.39) приобретает следующий вид.
(5.40)
Можете ли вы, изучив уравнение (5.40), предположить, чем следует руководствоваться при проектировании входного каскада приемника (особенно первого каскада или первой пары каскадов)? На входе приемника сигнал более уязвим к дополнительному шуму; следовательно, первый каскад должен иметь максимально низкий шум-фактор F1. Кроме того, поскольку шум-фактор каждого последующего каскада ослабляется на коэффициенты усиления предыдущих каскадов, это приводит к тому, что мы стремимся получить максимально возможный коэффициент G1. Одновременное получение максимально низкого F1, и максимально высокого G1 — задачи противоречивые; следовательно, всегда необходим некоторый компромисс.
а) б)
Рис. 5.17. Сети, соединенные последовательно
Уравнения (5.40) и (5.28) можно объединить и выразить эффективную шумовую температуру последовательности n каскадов.
(5.41)
На рис. 5.17, б показана питающая линия, последовательно соединенная с усилителем; после этого обычно следует принимающая антенна. Используя уравнение (5.39) для нахождения Fобщ подобной линии с потерями, можем записать следующее:
(5.42)
поскольку шум-фактор линии с потерями равен L, а коэффициент усиления линии — 1/L. По аналогии с уравнением (5.36) общую температуру можно записать следующим образом.
(5.43)
Общую температуру канала и усилителя можно также записать иначе.
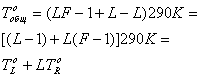(5.44)
5.5.4.1. Сравнение шум-фактора и шумовой температуры
Поскольку и шум-фактор F и эффективная шумовая температура Т° характеризуют шумовые характеристики устройств, некоторые инженеры вынуждены выбирать одну из этих мер. В то же время оба параметра имеет четко определенную "сферу деятельности". Для наземных приложений практически универсальным является шум-фактор F; здесь понятие ухудшения параметра SNR для источника с температурой 290 К имеет смысл, поскольку температура наземных источников обычно близка к 290 К. Значения наземных шум-факторов обычно принадлежат диапазону 1-10 дБ.
Для космических приложений более удобным критерием качества является параметр Т°. Диапазон температур для коммерческих систем обычно находится между 30 и 150 К. Недостатком использования шум-факторов для подобных малошумящих сетей является то, что все получаемые значения близки к единице (0,5-1,5 дБ), что создает определенные затруднения при сравнении устройств. Для малошумящих приложений F (в децибелах) необходимо выражать с точностью до двух знаков после запятой, чтобы оно давало разрешение или точность, сравнимую с точностью, которую дает To. Для приложений космической связи эталонная температура в 290 К не является настолько подходящей, как для наземных приложений. Если же использовать эффективную температуру, то для описания ухудшения никакой эталонной температуры не требуется (разве что абсолютный нуль К). Эффективная входная шумовая температура просто сравнивается с эффективной шумовой температурой источника. Вообще, приложения, в которых фигурируют малошумящие устройства, лучше описывать с помощью эффективной температуры, а не шум-фактора.
5.5.5. Эффективная температура системы
На рис. 5.18 представлена упрощенная схема принимающей системы, причем указаны те области (антенна, линия связи и предварительный усилитель), которые играют основную роль в ухудшении параметра SNR. Влияние предварительного усилителя уже обсуждалось ранее — оно заключается во введении в линию дополнительного шума. Также рассматривались потери в линии — сигнал поглощается при фиксированном уровне шума (если температура линии меньше (или равна) температуры источника). Оставшиеся источники ухудшения качества сигнала могут быть как естественными, так и искусственными. Естественные источники — это молнии, небесные источники радиоизлучения, атмосферные источники и тепловое излучение от земли и других физических структур. Искусственные — это излучение от автомобильных систем зажигания и других электрических приборов, а также радиопередача от других пользователей, использующих ту же полосу, что и приемник. Общий объем шума, вносимого перечисленными внешними источниками, можно описать как 
, где 
является температурой антенны. Антенна подобна линзе: вносимый ею шум определяется тем, "на что смотрит антенна". Если антенна нацелена на прохладную область неба, вводится крайне малый объем теплового шума. Температура антенны — это мера эффективной температуры, проинтегрированной по всей поверхности антенны.
Рис. 5.18. Основные источники шума принимающей системы
Теперь мы можем определить температуру системы Ts°, сложив все вклады в шум системы (выраженные через эффективную температуру). Суммарное выражение выглядит следующим образом.
(5.45)
Здесь, ТА° — температура антенны, а Tо6ш° — общая температура линии и предварительного усилителя. В уравнении (5.45) указаны два основных источника шума и интерференции, вызывающие ухудшение качества работы приемника. Один источник, описываемый членом ТА°, представляет ухудшение работоспособности, навязываемое "внешним миром", проходящим через антенну. Второй источник, описываемый членом Tо6ш°, — это тепловой шум, вызванный движением электронов во всех проводниках. Поскольку температура системы TS° — это новая суммарная температура, включающая ТА° и суммарную эффективную температуру линии и предварительного усилителя, может возникнуть вопрос: почему уравнение (5.45) не содержит тех же множителей последовательного уменьшения, что и в уравнении (5.41)? Мы предполагаем, что антенна не имеет диссипативных частей; ее коэффициент усиления, в отличие от усилителя или аттенюатора, может рассматриваться как коэффициент расширения спектра сигнала. Какая бы эффективная температура не вводилась при проходе через антенну, это не зависит от самой антенны; антенна представляет шум источника (или температуру источника) на входе линии.
Используя уравнение (5.44), мы можем модифицировать уравнение (5.45) следующим образом.
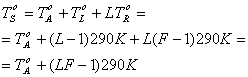(5.46)
(5.47)
Если LF выражено в децибелах, мы должны вначале изменить его размерность, и Ts° приобретет следующий вид.
Уравнения (5.45)-(5.47) описывают температуру системы ТS на оконечных устройствах принимающей антенны, а уравнения (5.10) и (5.11) — мощность Рr, полученную принимающей антенной. Данные определения используются в этой главе; кроме того, их предпочитают разработчики систем, антенн, а также люди, работающие на передающей стороне линии. Важно отметить, что существует альтернативный набор определений, используемых разработчиками систем, которые предпочитают описывать температуру системы 
и принятую мощность 
входе приемника. Если предположить, что антенна и приемник связаны устройством, которое не сложнее линии с потерями, то параметры Ts и отличаются в L раз (напомним, что L— коэффициент потерь в линии). Иными словами, 
. При вычислении принятого SNR (определяемого в следующем разделе) с помощью определений принятой мощности и температуры системы, соотнесенных с приемником, результат не будет отличаться от того, который был получен при использовании определений, связанных со входом приемника. Причина в том, что множитель L входит и в числитель, и в знаменатель отношения SNR, поэтому он просто сокращается.
Пример 5.5. Шум-фактор и температура шума
На входе приемника, показанном на рис. 5.19, а, шум-фактор равен 10 дБ, усиление равно 80 дБ, а ширина полосы — 6 МГц. Мощность сигнала на входе Si равна 10-11 Вт. Допустим, что потери в линии отсутствуют и температура антенны равна 150 К. Найдите ТR°, ТS°, Nout, (SNR)in и (SNR)out.
а)
б)
Рис. 5.19. Улучшение входного каскада приемника за счет малошумящего предварительного усилителя
Решение
Вначале преобразуем все значения в децибелах в размерные величины.
ТR° = (F- 1)290 К = 2610 К
изолированного уравнения (3.40) при L= 1 для малошумящей линии дает следующее.
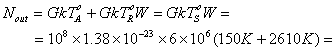
= 1,2 мкВт (вклад от источника) + 21,6 мкВт (вклад от входного каскада) = 22,8 мкВт
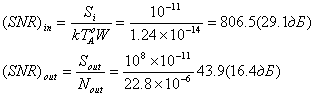
Заметим, что в приведенном примере шум усилителя значительно больше шума источника и является основной причиной ухудшения параметра SNR.
Пример 5.6. Улучшение параметра SNR с помощью малошумящего предварительного усилителя
Используйте предварительный усилитель, как показано на рис. 5.19, б, с шум-фактором 3 дБ, усилением 13 дБ и шириной полосы 6 МПц для улучшения SNR приемника, описанного в примере 5.5. Определите 
объединения предварительного усилителя и приемника. Найдите 
и (SNR)out. Потери в линии будем считать нулевыми.
Решение
Как и ранее, вначале все значения, выраженные в децибелах, приводятся к размерному виду.
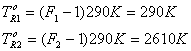
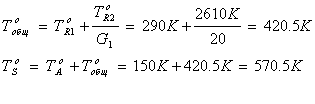
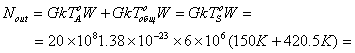
= 24,8 мкВт (вклад источника) + 69,6 мкВт (вклад входного каскада) = 94,4 мкВт
Итак, при добавлении предварительного усилителя выходной шум увеличивается (с 22,8 мкВт в примере 5.5) до 94,4 мкВт. И все же, несмотря на увеличение мощности шума, более низкая температура системы приводит к улучшению параметра SNR на 6,9 дБ (с 16,4 дБ в примере 5.5 до 23,3 дБ в данном примере). Цена, которую мы платим за это улучшение, — необходимость улучшения fo&u на 6 дБ (с 10 дБ в примере 5.5 до.4 дБ в данном примере).
Нежелательный Шум частично вносится посредством антенны (KTA°W) и частично генерируется внутренне в входном каскаде приемника (кТ06ш°W). Объем улучшения системы, который может дать проектирование входного каскада, зависит от того, какая часть общего шума вносится входным каскадом. Из примера 5.5 мы видели, что входной каскад вносит большую часть шума. Следовательно, как было сделано в примере 5.6, обеспечение малошумящего предварительного усилителя значительно улучшает системное отношение сигнал/шум (SNR). В следующем примере рассматривается, когда большая часть шума вносится посредством антенны; мы увидим, что в этом случае введение малошумящего предварительного усилителя не дает ощутимого улучшения параметра SNR.
Пример 5.7. Попытка улучшения SNR при больших значениях ТA°
Повторите примеры 5.6 и 5.5 с единственным изменением: пусть тA° =8000 К. Другими словами, большая часть шума теперь вносится антенной; допустим, все поле зрения антенны заполняет очень горячее тело (солнце). Вычислите улучшение параметра SNR, которое дается предварительным усилителем, использованным в примере 5.6 (рис. 5.19, б), после чего сравните результат с ответом примера 5.6.
Решение
Без предварительного усилителя
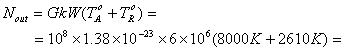
= 66,2 мкВт (вклад источника) + 21,6 мкВт (вклад входного каскада) = 87,8 мкВт
С предварительным усилителем
= 1324,8 мкВт (вклад источника) + 69,6 мкВт (вклад входного каскада)=1394,4 мкВт
Таким образом, в данном случае улучшение параметра SNR равно всего 1 дБ, что значительно меньше полученных ранее 6,9 дБ. Если основные источники шума находятся внутри приемника, улучшить SNR можно за счет введения малошумящих устройств. В то же время, если основные источники шума являются внешними, то улучшение входного каскада приемника не имеет существенного значения.
Шум-фактор — это определение, основанное на использовании эталонного значения 290 К. Если температура источника отличается от 290К, как в примерах 5.5—5.7, то необходимо определить рабочий или эффективный шум-фактор, описывающий реальную зависимость между (SNR)in и (SNR)out. Если в качестве отправной точки использовать уравнения (5.25) и (5.27), рабочий шум-фактор можно выразить следующим образом.
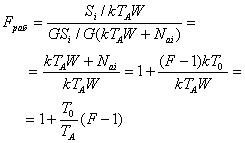(5.48)
5.5.6. Шумовая температура неба
Принимающая антенна собирает случайные шумы, излученные галактикой, солнцем и наземными источниками, что вместе составляет фоновый шум неба. Фон неба появляется как комбинация галактического воздействия, уменьшающегося с частотой, и атмосферного воздействия, которое становится существенным, при частоте порядка 10 ГГц (и увеличивается с частотой). Пример температуры неба, измеренной с земли, приведен на рис. 5.20 (учтены оба названных механизма). Заметим, что существует область между 1 и 10 ГГц, где температура достигает наименьшего значения; галактический шум становится достаточно малым при 1 ГГц и для спутниковой связи шум излучения абсолютно черного тела (вследствие поглощения атмосферой) не является существенным, если он ниже 10 ГГц. (Для других приложений, например пассивной радиометрии, это по-прежнему является проблемой.) Эта область, известная как микроволновое (или космическое) окно, представляет особый интерес для спутниковой связи или космической дальней связи. Низкий шум неба — это основная причина того, что системы в основном используют несущие частоты, принадлежащие этой части спектра. Кривые на рис. 5.20, показывающие галактический и атмосферный шумы, показаны в виде семейства кривых с разными углами возвышения θ. При θ = 0 принимающая антенна направлена на линию горизонта, и в процессе распространения сигнал проходит наибольший возможный путь через атмосферу. При θ = 90° антенна направлена на зенит, и минимальная часть пути сигнала приходится на атмосферу. Таким образом, верхняя кривая семейства демонстрирует почти наихудшую (почти — потому что погода считается ясной) зависимость температуры шума от частоты, а нижняя представляет наиболее благоприятный случай. На рис. 5.20 также показан график зависимости температуры шума от частоты при дожде. Поскольку интенсивность любого ливня можно выразить только статистически, показанные температуры шума — это значения, когда дожди идут 25% времени (в зените). Какая спектральная область является наиболее благоприятной для космической связи, если принимать во внимание дожди? Это нижняя часть космического окна. По этой причине системы, подобные SGLS (Space Ground Link Subsystem) (военные) и Unified S-Band Telemetry, Tracking, and Control System (NASA), расположены в полосе частот 1,8-2,4 ГГц.
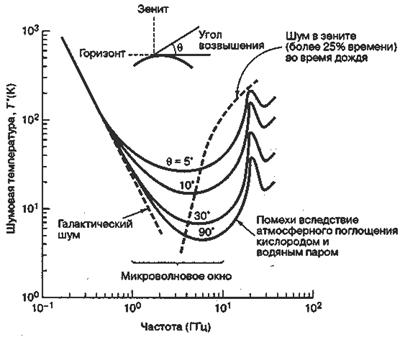
Рис. 5.20. Шумовая температура неба
5.5.6.1. Радиокарта неба
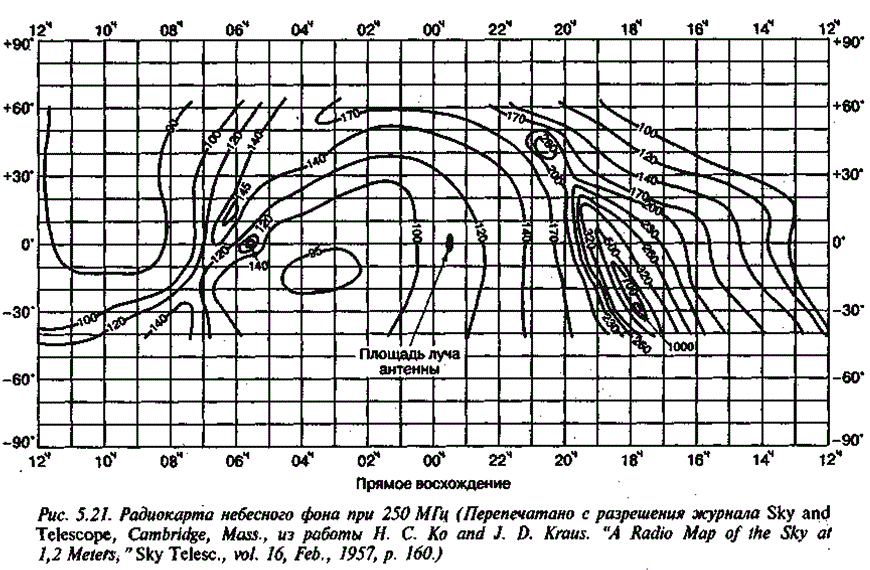
Различные исследователи изображали излучение галактического шума как функцию частоты. На рис. 5.21 представлена подобная карта радиотемператур, взятая из работы [12]. На ней изображены температурные контуры неба в районе 250 МГц при рассмотрении с земли. Вообще, небо состоит из локализированных галактических источников (Солнце, Луна, планеты и т.д.), каждый из которых имеет собственную температуру. Карта — это эффективная взвешенная сумма температур отдельных галактических источников плюс постоянный фон неба. Координаты карты, склонение и прямое восхождение, можно рассматривать как небесную широту и долготу относительно земной поверхности (прямое восхождение измеряется в часовых углах, причем 24 часа соответствуют полному обороту Земли). На рис. 5.21 температурные контуры показаны для температур от 90 до 1000 К. Измерения проводились так, чтобы воздействие Солнца было исключено (ночное небо). Луч антенны в центре карты указывает размер области неба, в пределах которой производились измерения (каждое измерение — это усреднение по площади луча). Чем уже луч, тем лучше разрешение температурных контуров; чем шире луч, тем разрешение хуже.
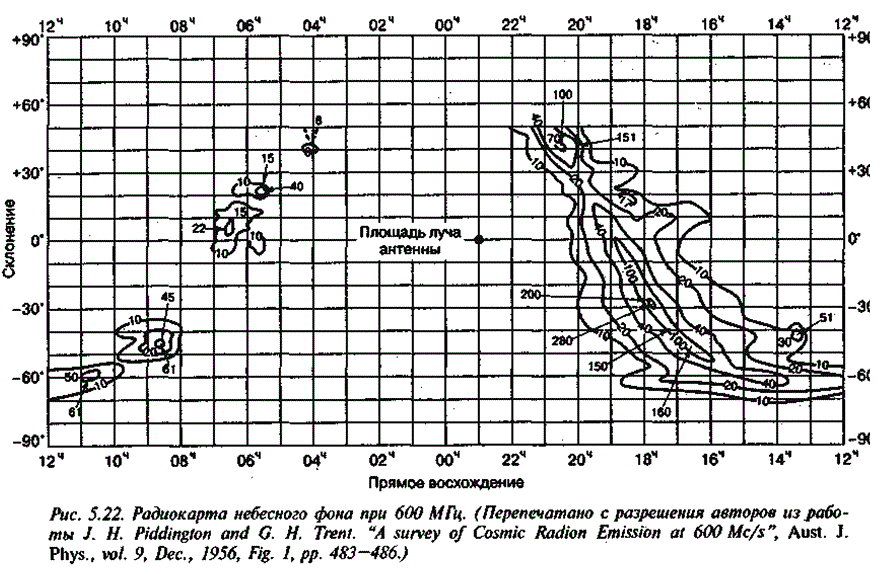
На рис. 5.22 представлена другая радиокарта для частоты 600 МГц, взятая из работы [13]. При этой частоте, как было показано на рис. 5.20, галактический шум снижается, по сравнению с рис. 5.21; наиболее низкой из показанных температур является 8 К, наиболее высокой — 280 К. Если внимательно изучить рис. 5.21 и 5.22, то можно обнаружить область наибольшего излучения шума. Она расположена в овальной области в середине правой части каждой карты; продольная ось овала определяет положение на нашей галактической плоскости, где подобное излучение космического шума является наиболее интенсивным.
